Модель следования за автомобилем Ньюэлла

Эта статья в значительной степени или полностью основана на одном источнике . Соответствующее обсуждение можно найти на странице обсуждения . Пожалуйста, помогите улучшить эту статью, добавив ссылки на дополнительные источники . Найти источники:  "Модель следования за автомобилем Ньюэлла" – новости  · газеты  · книги  · ученый  · JSTOR ( декабрь 2009 г. )

В теории транспортных потоков модель следования автомобилей Ньюэлла — это метод, используемый для определения того, как транспортные средства следуют друг за другом на дороге. Основная идея этой модели заключается в том, что транспортное средство будет поддерживать минимальный пространственный и временной зазор между собой и транспортным средством, которое идет впереди. Таким образом, в условиях перегруженности , если ведущий автомобиль изменит свою скорость, следующий за ним автомобиль также изменит скорость в точке во времени-пространстве вдоль скорости волны трафика , -w . ^[1]

Предполагая, что фундаментальная диаграмма (плотность потока) является треугольной функцией, можно предположить состояние трафика A со скоростью v _A и плотностью k _A в области затора. Плотность на проезжей части может быть определена с использованием расстояния между транспортными средствами и вычисляется просто уравнением:

к _А = 1/с _А

Геометрические соотношения из фундаментальной диаграммы можно использовать и для расчета плотности, заданной уравнением:

к _А = ( к _j w )/( v _A +w )

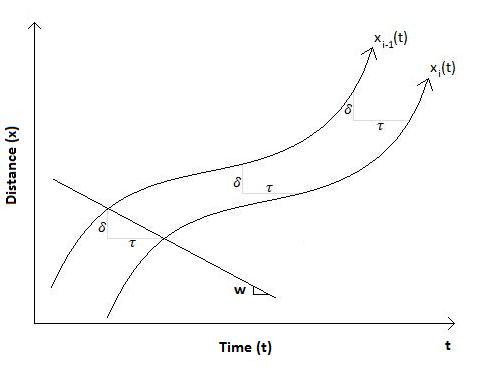
На пространственно-временной диаграмме траектории ведущего (вверху) и следующего (внизу) транспортного средства разделены расстоянием δ и временем τ . Расстояние между транспортными средствами в состоянии движения A можно найти с помощью геометрического соотношения, найденного на пространственно-временной диаграмме:

с _А = v _А ( τ ) + δ

Используя соотношения между предыдущими уравнениями, можно найти переменные τ и δ :

τ = 1 /( wk _j )

δ = 1 / к _j

Таким образом, τ и δ являются константами, определяемыми скоростью волны и плотностью пробки, независимо от скорости ведущего транспортного средства и состояния дорожного движения. Путь транспортного средства i , как функция времени, можно определить с помощью уравнения:

x _i ( t ) = min( x _A ^F ( t ), x _A ^C ( t ))

Положение транспортного средства i в условиях свободного движения:

x _i ^F ( t ) = x _i ( t-τ ) + v _f * τ

Положение транспортного средства i в условиях загруженности:

x _i ^C ( t ) = x _i-1 ( t-τ ) - δ

В реальных условиях гипотетический водитель, следующий за автомобилем, может вести машину неправильно, что приведет к отклонениям от пространственно-временных траекторий, предложенных в модели Ньюэлла. Пространственно-временные траектории, полученные на основе данных, собранных на дорогах и автомагистралях, можно сравнить с соответствующей траекторией модели следования за автомобилем Ньюэлла, чтобы определить, осторожен или агрессивен водитель. На следующих рисунках показаны траектории двух автомобилей (черные) и траектория, предсказанная моделью следования за автомобилем Ньюэлла для следующего автомобиля (синяя).

Пространственно-временная траектория для обычного водителя:

Пространственно-временная траектория для осторожного водителя:

Траектория времени и пространства для агрессивного водителя:

Когда водитель, следующий за ним, реагирует рано при замедлении или поздно при ускорении, разрыв во времени и расстоянии между лидером и последователем увеличивается. Последующего можно охарактеризовать как осторожного водителя. В другой ситуации, последователь реагирует позже при замедлении или раньше при ускорении, уменьшая разрыв во времени и расстоянии между лидером и последователем. Последующего можно охарактеризовать как агрессивного водителя.

• Среднегодовой дневной трафик
• модель Джиппса
• Интеллектуальная модель водителя
• Моделирование дорожного движения