Многоконусный
Сравнение периодограммы (черный) и многоконусной оценки (красный) единичного пробного измерения локального полевого потенциала. Эта оценка использовала 9 конусов.

В обработке сигналов многоконтурный анализ представляет собой метод оценки спектральной плотности, разработанный Дэвидом Дж. Томсоном . [1] [2] Он позволяет оценить спектр мощности S X стационарного эргодического конечно-дисперсионного случайного процесса X , если в качестве данных задана конечная непрерывная реализация X.

Мотивация

Метод multitaper преодолевает некоторые ограничения непараметрического анализа Фурье . Применяя преобразование Фурье для извлечения спектральной информации из сигнала, мы предполагаем, что каждый коэффициент Фурье является надежным представлением амплитуды и относительной фазы соответствующей частоты компонента. Однако это предположение, как правило, недействительно для эмпирических данных. Например, одно испытание представляет собой только одну шумную реализацию основного интересующего процесса. Подобная ситуация возникает в статистике при оценке мер центральной тенденции , т. е. плохая практика оценивать качества популяции с использованием отдельных лиц или очень малых выборок. Аналогично, один образец процесса не обязательно обеспечивает надежную оценку его спектральных свойств. Более того, наивная спектральная плотность мощности , полученная из необработанного преобразования Фурье сигнала, является смещенной оценкой истинного спектрального содержимого.

Важность усреднения при оценке (кросс-)спектральной плотности. [3] (a) Синтетически сгенерированный шумовой сигнал с двумя когерентными частотами на 0,03 и 0,6 Гц. (b) Оценки спектральной плотности Multitaper (MT). (c) Оценки квадрата когерентности с использованием анализа Slepian multitaper (толстая линия, незаштрихованная) и анализа перекрывающихся сегментов Welch (WOSA) (тонкая линия, заштрихованная область). (d) Оценка фазы оценки кросс-спектральной плотности с использованием MT (сплошная) и WOSA (пунктирная). При 0,03 Гц сигналы находятся в фазе, а при 0,6 Гц они не совпадают по фазе. − π / 4 {\displaystyle -\пи /4}

Эти проблемы часто преодолеваются путем усреднения по многим реализациям одного и того же события после применения сужения к каждому испытанию. Однако этот метод ненадежен с небольшими наборами данных и нежелателен, когда нежелательно ослаблять компоненты сигнала, которые различаются между испытаниями. Более того, даже когда доступно много испытаний, несужающаяся периодограмма , как правило, смещена (за исключением белого шума), и смещение зависит от длины каждой реализации, а не от количества зарегистрированных реализаций. Применение одного сужения уменьшает смещение, но за счет увеличения дисперсии оценщика из-за ослабления активности в начале и конце каждого записанного сегмента сигнала.

Метод многоконтурного сужения частично устраняет эти проблемы, получая несколько независимых оценок из одного и того же образца. Каждое сужение данных умножается поэлементно на сигнал, чтобы обеспечить оконный эксперимент, из которого оценивается мощность на каждой частоте компонента. Поскольку каждое сужение попарно ортогонально всем другим сужениям, оконные функции не коррелируют друг с другом. Окончательный спектр получается путем усреднения по всем сужающимся спектрам, таким образом восстанавливая часть информации, которая теряется из-за частичного затухания сигнала, возникающего в результате применения отдельных сужений.

Этот метод особенно полезен, когда доступно небольшое количество испытаний, поскольку он уменьшает дисперсию оценщика сверх того, что возможно при методах с одним сужением. Более того, даже когда доступно много испытаний, подход с несколькими сужениями полезен, поскольку он позволяет более строго контролировать компромисс между смещением и дисперсией, чем это возможно в случае с одним сужением.

Томсон выбрал функции Слепиана [4] или дискретные вытянутые сфероидальные последовательности в качестве конусов, поскольку эти векторы взаимно ортогональны и обладают желаемыми свойствами спектральной концентрации (см. раздел о последовательностях Слепиана). На практике взвешенное среднее часто используется для компенсации возросшей потери энергии при конусах более высокого порядка. [5]

Формулировка

Рассмотрим p-мерный стационарный стохастический процесс с нулевым средним

Х ( т ) = [ Х ( 1 , т ) , Х ( 2 , т ) , … , Х ( п , т ) ] Т {\displaystyle \mathbf {X} (t)={\lbrack X(1,t),X(2,t),\dots ,X(p,t)\rbrack }^{T}}

Здесь T обозначает транспонирование матрицы. Например, в нейрофизиологии p относится к общему числу каналов и, следовательно, может представлять одновременное измерение электрической активности этих p каналов. Пусть интервал выборки между наблюдениями будет , так что частота Найквиста будет . Х ( т ) {\displaystyle \mathbf {X} (т)} Δ т {\displaystyle \Дельта t} ф Н = 1 / ( 2 Δ т ) {\displaystyle f_{N}=1/(2\Delta t)}

Многоконтурный спектральный оценщик использует несколько различных конических значений данных, которые ортогональны друг другу. Многоконтурный кросс-спектральный оценщик между каналами l и m является средним значением K прямых кросс-спектральных оценщиков между той же парой каналов ( l и m ) и, следовательно, принимает форму

С ^ л м ( ф ) = 1 К ∑ к = 0 К − 1 С ^ к л м ( ф ) . {\displaystyle {\hat {S}}^{lm}(f)={\frac {1}{K}}\sum _{k=0}^{K-1}{\hat {S}}_{k}^{lm}(f).}

Здесь (для ) — k -я прямая кросс-спектральная оценка между каналами l и m , которая определяется как С ^ к л м ( ф ) {\displaystyle {\hat {S}}_{k}^{lm}(f)} 0 ≤ к ≤ К − 1 {\displaystyle 0\leq k\leq K-1}

С ^ к л м ( ф ) = 1 Н Δ т [ Дж. к л ( ф ) ] ∗ [ Дж. к м ( ф ) ] , {\displaystyle {\hat {S}}_{k}^{lm}(f)={\frac {1}{N\Delta t}}{\lbrack J_{k}^{l}(f)\rbrack }^{*}{\lbrack J_{k}^{m}(f)\rbrack },}

где

Дж. к л ( ф ) = ∑ т = 1 Н час т , к Х ( л , т ) е − я 2 π ф т Δ т . {\displaystyle J_{k}^{l}(f)=\sum _{t=1}^{N}h_{t,k}X(l,t)e^{-i2\pi ft\Delta t}.}
Три ведущие последовательности Слепиана для T = 1000 и 2WT = 6. Обратите внимание, что каждая последовательность более высокого порядка имеет дополнительное нулевое пересечение.

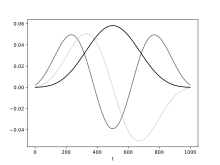
Последовательности Слепяна

Последовательность представляет собой сужение данных для k -й прямой кросс-спектральной оценки и выбирается следующим образом: { час т , к } {\displaystyle \lbrace h_{t,k}\rbrace } С ^ к л м ( ф ) {\displaystyle {\hat {S}}_{k}^{lm}(f)}

Мы выбираем набор из K ортогональных конусов данных, так что каждый из них обеспечивает хорошую защиту от утечки. Они задаются последовательностями Слепяна [6] по имени Дэвида Слепяна (также известными в литературе как дискретные вытянутые сфероидальные последовательности или сокращенно DPSS) с параметром W и порядками k  = 0 до K  − 1. Максимальный порядок K выбирается меньшим числа Шеннона . Величина 2 W определяет полосу пропускания разрешения для задачи спектральной концентрации и . Когда l  =  m , мы получаем многоконтурную оценку для автоспектра l -го канала. В последние годы в качестве сверхполной альтернативы DPSS был предложен словарь, основанный на модулированном DPSS. [7] 2 Н Вт Δ т {\displaystyle 2NW\Дельта t} Вт ∈ ( 0 , ф Н ) {\displaystyle W\in (0,f_{N})}

См. также Оконная функция: DPSS или окно Слепяна

Приложения

Не ограничиваясь временными рядами, метод multitaper легко расширяется до нескольких декартовых измерений с использованием пользовательских функций Slepian [8] и может быть переформулирован для спектральной оценки на сфере с использованием функций Slepian, построенных из сферических гармоник [9] для приложений в геофизике и космологии [10] [11] среди других. Обширное рассмотрение применения этого метода для анализа многопробных, многоканальных данных, полученных в нейронауке , биомедицинской инженерии и других областях, можно найти здесь. В настоящее время этот метод используется в наборе инструментов спектрального анализа Chronux .

Смотрите также

Ссылки

  1. ^ Томсон, DJ (1982) Оценка спектра и гармонический анализ . Труды IEEE , 70, 1055–1096
  2. ^ * Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Раздел 13.4.3. Методы многоконтурности и функции Слепиана ", Numerical Recipes: The Art of Scientific Computing (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
  3. ^ Саймонс, Ф.Дж.; Коренага, Дж.; Зубер, М.Т. (2000). «Изостатическая реакция австралийской литосферы: оценка эффективной упругой толщины и анизотропии с использованием многоконтурного анализа». 105 (B8): 19163-19184. {{cite journal}}: Цитировать журнал требует |journal=( помощь )
  4. ^ Саймонс, Ф. Дж.; Платтнер, А. (2015). «Скалярные и векторные функции Слепиана, оценка сферического сигнала и спектральный анализ». Справочник по геоматематике . С. 2563–2608. doi :10.1007/978-3-642-54551-1_30. ISBN 978-3-642-54550-4.
  5. ^ Персиваль, ДБ и А. Т. Уолден. Спектральный анализ для физических приложений: многоконусные и обычные одномерные методы . Кембридж: Cambridge University Press, 1993.
  6. ^ Слепян, Д. (1978) «Вытянутые сфероидальные волновые функции, анализ Фурье и неопределенность – V: Дискретный случай». Bell System Technical Journal , 57, 1371–1430
  7. ^ E. Sejdić, M. Luccini, S. Primak, K. Baddour, T. Willink, «Оценка канала с использованием модулированных дискретных вытянутых сфероидальных последовательностей на основе кадров», в Трудах Международной конференции IEEE по акустике, речи и обработке сигналов (ICASSP 2008) , Лас-Вегас, Невада, США, 31 марта - 4 апреля 2008 г., стр. 2849-2852.
  8. ^ Саймонс, Ф. Дж.; Ванг, Д. В. (2011). «Пространственно-спектральная концентрация в декартовой плоскости». GEM: Международный журнал геоматематики . 2 : 1–36. doi :10.1007/s13137-011-0016-z..
  9. ^ Simons, FJ; Dahlen, FA; Wieczorek, MA (2006). «Пространственно-спектральная концентрация на сфере». Обзор SIAM . 48 (3): 504–536. arXiv : math/0408424 . Bibcode : 2006SIAMR..48..504S. doi : 10.1137/S0036144504445765.
  10. ^ Wieczorek, MA; Simons, FJ (2007). "Минимально-дисперсионная многоконтурная спектральная оценка на сфере". Журнал анализа Фурье и приложений . 13 (6): 665. doi :10.1007/s00041-006-6904-1.
  11. ^ Дален, ФА; Саймонс, ФДж (2008). «Оценка спектра на сфере в геофизике и космологии». Geophysical Journal International . 174 (3): 774. arXiv : 0705.3083 . Bibcode : 2008GeoJI.174..774D. doi : 10.1111/j.1365-246X.2008.03854.x .
  • [1] Библиотеки C++/Octave для метода multitaper, включая адаптивное взвешивание (размещены на GitHub)
  • [2] Документация по методу многоконусности из реализации набора инструментов SSA-MTM
  • [3] Библиотека Fortran 90 с дополнительными многомерными приложениями
  • [4] База кода MATLAB для генерации сферических скалярных функций Слепиана
  • [5] База кода MATLAB для выполнения сферического многоконусного анализа
  • [6] База кода MATLAB для генерации декартовых функций Слепиана
  • [7] База кода MATLAB для генерации сферических векторных функций Слепяна
  • [8] Модуль Python
  • [9] R (язык программирования) многоконтурный пакет
  • [10] Скрипт S-Plus для генерации последовательностей Слепяна (dpss)
Взято с "https://en.wikipedia.org/w/index.php?title=Multitaper&oldid=1237357648"