Правило рандомизированного решения

В статистической теории принятия решений рандомизированное решающее правило или смешанное решающее правило — это решающее правило , которое связывает вероятности с детерминированными решающими правилами. В конечных задачах принятия решений рандомизированные решающие правила определяют множество рисков , которое является выпуклой оболочкой точек риска нерандомизированных решающих правил.

Поскольку всегда существуют нерандомизированные альтернативы рандомизированным правилам Байеса, рандомизация не нужна в байесовской статистике , хотя частотная статистическая теория иногда требует использования рандомизированных правил для удовлетворения условий оптимальности, таких как минимакс , особенно при выводе доверительных интервалов и проверке гипотез о дискретных распределениях вероятностей .

Статистический тест, использующий правило рандомизированного принятия решений, называется рандомизированным тестом .

Пусть будет набором нерандомизированных правил принятия решений с соответствующими вероятностями . Тогда рандомизированное правило принятия решений определяется как и его связанная функция риска равна . ^[1] Это правило можно рассматривать как случайный эксперимент , в котором правила принятия решений выбираются с соответствующими вероятностями. ^[2]${\displaystyle {\mathcal {D}}=\{d_{1},d_{2}...,d_{h}\}}$${\displaystyle p_{1},p_{2},...,p_{h}}$${\displaystyle d^{*}}$${\displaystyle \sum _{i=1}^{h}p_{i}d_{i}}$ ${\displaystyle R(\theta ,d^{*})}$${\displaystyle \sum _{i=1}^{h}p_{i}R(\theta ,d_{i})}$${\displaystyle d_{1},...,d_{h}\in {\mathcal {D}}}$${\displaystyle p_{1},...p_{h}}$

В качестве альтернативы, рандомизированное правило принятия решений может назначать вероятности непосредственно элементам пространства действий для каждого члена выборочного пространства. Более формально, обозначает вероятность того, что действие выбрано. При таком подходе его функция потерь также определяется непосредственно как: . ^[3]${\displaystyle {\mathcal {A}}}$${\displaystyle d^{*}(x,A)}$${\displaystyle a\in {\mathcal {A}}}$${\displaystyle \int _{A\in {\mathcal {A}}}d^{*}(x,A)L(\theta ,A)dA}$

Введение рандомизированных правил принятия решений, таким образом, создает большее пространство принятия решений, из которого статистик может выбирать свое решение. Поскольку нерандомизированные правила принятия решений являются особым случаем рандомизированных правил принятия решений, где одно решение или действие имеет вероятность 1, исходное пространство принятия решений является надлежащим подмножеством нового пространства принятия решений . ^[4]${\displaystyle {\mathcal {D}}}$${\displaystyle {\mathcal {D}}^{*}}$

Как и в случае с нерандомизированными правилами принятия решений, рандомизированные правила принятия решений могут удовлетворять благоприятным свойствам, таким как допустимость, минимаксность и Байес. Это будет проиллюстрировано в случае конечной задачи принятия решений, т. е. задачи, где пространство параметров представляет собой конечный набор, скажем, элементов. Набор рисков, далее обозначаемый как , представляет собой набор всех векторов, в котором каждый элемент является значением функции риска, связанной с рандомизированным правилом принятия решений при определенном параметре: он содержит все векторы вида . Обратите внимание, что по определению рандомизированного правила принятия решений набор рисков представляет собой выпуклую оболочку рисков . ^[5]${\displaystyle k}$${\displaystyle {\mathcal {S}}}$${\displaystyle (R(\theta _{1},d^{*}),...R(\theta _{k},d^{*})),d^{*}\in {\mathcal {D}}^{*}}$${\displaystyle (R(\theta _{1},d),...R(\theta _{k},d)),d\in {\mathcal {D}}}$

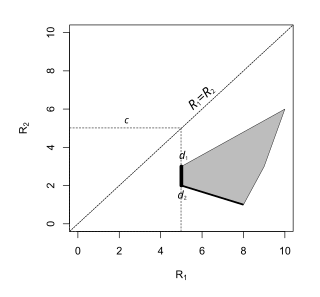
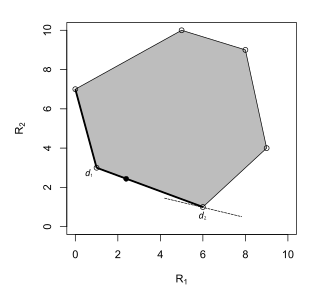
В случае, когда пространство параметров имеет только два элемента и , это составляет подмножество , поэтому его можно нарисовать относительно осей координат и , соответствующих рискам под и соответственно. ^[6] Пример показан справа.${\displaystyle \theta _{1}}$${\displaystyle \theta _{2}}$${\displaystyle \mathbb {R} ^{2}}$${\displaystyle R_{1}}$${\displaystyle R_{2}}$${\displaystyle \theta _{1}}$${\displaystyle \theta _{2}}$

Допустимое правило принятия решений — это правило, которое не доминируется никаким другим правилом принятия решений, т. е. не существует правила принятия решений, которое имеет такой же риск или меньший риск, чем оно для всех параметров, и строго меньший риск, чем оно для некоторого параметра. В конечной задаче принятия решений точка риска допустимого правила принятия решений имеет либо меньшие x-координаты, либо y-координаты, чем все другие точки риска, или, более формально, это набор правил с точками риска вида , таким образом, что . Таким образом, левая сторона нижней границы набора рисков является набором допустимых правил принятия решений. ^{[6] [7]}${\displaystyle (a,b)}$${\displaystyle \{(R_{1},R_{2}):R_{1}\leq a,R_{2}\leq b\}\cap {\mathcal {S}}=(a,b)}$

Минимаксное правило Байеса — это правило, которое минимизирует риск супремума среди всех правил принятия решений в . Иногда рандомизированное правило принятия решений может работать лучше, чем все другие нерандомизированные правила принятия решений в этом отношении. ^[1]${\displaystyle \sup _{\theta \in \Theta }R(\theta ,d^{*})}$${\displaystyle {\mathcal {D}}^{*}}$

В конечной задаче принятия решений с двумя возможными параметрами правило минимакса можно найти, рассмотрев семейство квадратов . ^[8] Значение для наименьшего из таких квадратов, которые касаются, является риском минимакса, а соответствующая точка или точки на множестве рисков являются правилом минимакса.${\displaystyle Q(c)=\{(R_{1},R_{2}):0\leq R_{1}\leq c,0\leq R_{2}\leq c\}}$${\displaystyle c}$${\displaystyle {\mathcal {S}}}$

Если набор рисков пересекает линию , то допустимое правило принятия решения, лежащее на линии, является минимаксным. Если или выполняется для каждой точки набора рисков, то правило минимакса может быть либо крайней точкой (т. е. нерандомизированным правилом принятия решения), либо линией, соединяющей две крайние точки (нерандомизированные правила принятия решения). ^{[9] [6]}${\displaystyle R_{1}=R_{2}}$${\displaystyle R_{2}>R_{1}}$${\displaystyle R_{1}>R_{2}}$

• 
  Правило минимакса — это правило рандомизированного принятия решений .${\displaystyle (1-p)d_{1}+pd_{2}}$
• 
  Правило минимакса таково .${\displaystyle d_{2}}$
• 
  Правила минимакса — это все правила вида , .${\displaystyle (1-p)d_{1}+pd_{2}}$${\displaystyle 0\leq p\leq 1}$

Рандомизированное правило Байеса — это правило, которое имеет инфимум байесовского риска среди всех правил принятия решений. В особом случае, когда пространство параметров состоит из двух элементов, линия , где и обозначают априорные вероятности и соответственно, является семейством точек с байесовским риском . Таким образом, минимальный байесовский риск для задачи принятия решений является наименьшим, таким, что линия касается набора рисков. ^{[10] [11]} Эта линия может либо касаться только одной крайней точки набора рисков, т. е. соответствовать нерандомизированному правилу принятия решений, либо перекрывать всю сторону набора рисков, т. е. соответствовать двум нерандомизированным правилам принятия решений и рандомизированным правилам принятия решений, объединяющим их. Это иллюстрируется тремя ситуациями ниже:${\displaystyle r(\pi ,d^{*})}$${\displaystyle \pi _{1}R_{1}+(1-\pi _{1})R_{2}=c}$${\displaystyle \pi _{1}}$${\displaystyle \pi _{2}}$${\displaystyle \theta _{1}}$${\displaystyle \theta _{2}}$${\displaystyle c}$${\displaystyle c}$

• 
  Правила Байеса представляют собой набор правил принятия решений в форме , .${\displaystyle (1-p)d_{1}+pd_{2}}$${\displaystyle 0\leq p\leq 1}$
• 
  Правило Байеса таково .${\displaystyle d_{1}}$
• 
  Правило Байеса таково .${\displaystyle d_{2}}$

Поскольку различные априорные вероятности приводят к различным наклонам, набор всех правил, которые являются байесовскими по отношению к некоторым априорным вероятностям, совпадает с набором допустимых правил. ^[12]

Обратите внимание, что невозможна ситуация, когда нерандомизированное правило Байеса не существует, а рандомизированное правило Байеса существует. Существование рандомизированного правила Байеса подразумевает существование нерандомизированного правила Байеса. Это также верно в общем случае, даже при бесконечном пространстве параметров, бесконечном байесовском риске и независимо от того, может ли быть достигнут инфимум байесовского риска. ^{[3] [12]} Это подтверждает интуитивное представление о том, что статистику не нужно использовать рандомизацию для принятия статистических решений. ^[4]

Поскольку рандомизированные правила Байеса всегда имеют нерандомизированные альтернативы, они не нужны в байесовской статистике . Однако в частотной статистике рандомизированные правила теоретически необходимы в определенных ситуациях, ^[13] и считались полезными на практике, когда они были впервые изобретены: Эгон Пирсон предсказал, что они «не встретят сильных возражений». ^[14] Однако в настоящее время лишь немногие статистики фактически применяют их. ^{[14] [15]}

Рандомизированные тесты не следует путать с тестами перестановки . ^[16]

В обычной формулировке теста отношения правдоподобия нулевая гипотеза отклоняется всякий раз, когда отношение правдоподобия меньше некоторой константы , и принимается в противном случае. Однако это иногда проблематично, когда является дискретным при нулевой гипотезе, когда это возможно.${\displaystyle \Lambda }$${\displaystyle K}$${\displaystyle \Lambda }$${\displaystyle \Lambda =K}$

Решение состоит в определении тестовой функции , значение которой представляет собой вероятность принятия нулевой гипотезы: ^{[17] [18]}${\displaystyle \phi (x)}$

${\displaystyle \phi (x)=\left\{{\begin{array}{l}1&{\text{ if }}\Lambda >K\\p(x)&{\text{ if }}\Lambda =K\\0&{\text{ if }}\Lambda <K\end{array}}\right.}$

Это можно интерпретировать как подбрасывание несимметричной монеты с вероятностью выпадения орла в любой момент и отклонение нулевой гипотезы, если выпадет орел. ^[15]${\displaystyle p(x)}$${\displaystyle \Lambda =k}$

Обобщенная форма леммы Неймана-Пирсона утверждает, что этот тест имеет максимальную мощность среди всех тестов на том же уровне значимости , что такой тест должен существовать для любого уровня значимости , и что этот тест является уникальным в нормальных ситуациях. ^[19]${\displaystyle \alpha }$${\displaystyle \alpha }$

В качестве примера рассмотрим случай, когда базовое распределение — это распределение Бернулли с вероятностью , и мы хотели бы проверить нулевую гипотезу против альтернативной гипотезы . Естественно выбрать некоторые такие, что , и отвергнуть нулевую гипотезу всякий раз , когда , где — тестовая статистика. Однако, чтобы учесть случаи, когда , мы определяем тестовую функцию:${\displaystyle p}$${\displaystyle p\leq \lambda }$${\displaystyle p>\lambda }$${\displaystyle k}$${\displaystyle P({\hat {p}}>k|H_{0})=\alpha }$${\displaystyle {\hat {p}}>k}$${\displaystyle {\hat {p}}}$${\displaystyle {\hat {p}}=k}$

${\displaystyle \phi (x)=\left\{{\begin{array}{l}1&{\text{ if }}{\hat {p}}>k\\\gamma &{\text{ if }}{\hat {p}}=k\\0&{\text{ if }}{\hat {p}}<k\end{array}}\right.}$

где выбрано так, что .${\displaystyle \gamma }$${\displaystyle P({\hat {p}}>k|H_{0})+\gamma P({\hat {p}}=k|H_{0})=\alpha }$

Аналогичная проблема возникает при построении доверительных интервалов. Например, интервал Клоппера-Пирсона всегда консервативен из-за дискретной природы биномиального распределения. Альтернативой является нахождение верхнего и нижнего доверительных пределов и решение следующих уравнений: ^[14]${\displaystyle U}$${\displaystyle L}$

${\displaystyle \left\{{\begin{array}{l}Pr({\hat {p}}<k|p=U)+\gamma P({\hat {p}}=k|p=U)&=\alpha /2\\Pr({\hat {p}}>k|p=L)+\gamma P({\hat {p}}=k|p=L)&=\alpha /2\end{array}}\right.}$

где — равномерная случайная величина на (0, 1).${\displaystyle \gamma }$

• Смешанная стратегия
• Линейное программирование

• Агрести, Алан; Готтард, Анна (2005). «Комментарий: Рандомизированные доверительные интервалы и подход Mid-P» (PDF) . Статистическая наука . 5 (4): 367–371. doi : 10.1214/088342305000000403 .
• Бикель, Питер Дж.; Доксум, Кьелл А. (2001). Математическая статистика: основные идеи и избранные темы (2-е изд.). Верхняя Сэддл-Ривер, Нью-Джерси: Prentice-Hall. ISBN 978-0138503635.
• ДеГрут, Моррис Х. (2004). Оптимальные статистические решения . Хобокен, Нью-Джерси: Wiley-Interscience. ISBN 978-0471680291.
• Пармиджани, Джованни; Иноуэ, Лурдес YT (2009). Теория принятия решений: принципы и подходы . Чичестер, Западный Суссекс: John Wiley and Sons. ISBN 9780470746684.
• Роберт, Кристиан П. (2007). Байесовский выбор: от теоретических основ принятия решений до вычислительной реализации . Нью-Йорк: Springer. ISBN 9780387715988.
• Янг, GA; Смит, RL (2005). Основы статистического вывода . Кембридж: Издательство Кембриджского университета. ISBN 9780521548663.