Теорема когерентности Маклейна

В теории категорий , разделе математики, теорема о когерентности Маклейна утверждает, по словам Сондерса Маклейна , «каждая диаграмма коммутирует». [1] Но относительно результата о некоторых коммутативных диаграммах Келли утверждает следующее: «больше не может рассматриваться как составляющий сущность теоремы о когерентности». [2] Точнее (ср. #Контрпример), она утверждает, что каждая формальная диаграмма коммутирует, где «формальная диаграмма» является аналогом правильно построенных формул и терминов в теории доказательств .

Теорему можно сформулировать как результат строгой конкретизации, а именно: каждая моноидальная категория моноидально эквивалентна строгой моноидальной категории. [3]

Контрпример

Неразумно ожидать , что мы сможем показать буквально каждую диаграмму коммутации, учитывая следующий пример Исбелла. [4]

Пусть будет скелетом категории множеств и D — единственное счетное множество в нем; отметим по единственности. Пусть будет проекцией на первый множитель. Для любых функций имеем . Теперь предположим, что естественные изоморфизмы являются тождественными; в частности, это имеет место для . Тогда для любого , поскольку — тождественное и является естественным, С е т 0 ⊂ С е т {\displaystyle {\mathsf {Набор}}_{0}\subset {\mathsf {Набор}}} Д × Д = Д {\displaystyle D\times D=D} п : Д = Д × Д → Д {\displaystyle p:D=D\times D\to D} ф , г : Д → Д {\displaystyle f,g:D\to D} ф ∘ п = п ∘ ( ф × г ) {\displaystyle f\circ p=p\circ (f\times g)} α : Х × ( И × З ) ≃ ( Х × И ) × З {\displaystyle \alpha:X\times (Y\times Z)\simeq (X\times Y)\times Z} Х = И = З = Д {\displaystyle X=Y=Z=D} ф , г , час : Д → Д {\displaystyle f,g,h:D\to D} α {\displaystyle \альфа}

ф ∘ п = п ∘ ( ф × ( г × час ) ) = п ∘ α ∘ ( ф × ( г × час ) ) = п ∘ ( ( ф × г ) × час ) ∘ α = ( ф × г ) ∘ п {\displaystyle f\circ p=p\circ (f\times (g\times h))=p\circ \alpha \circ (f\times (g\times h))=p\circ ((f\times g)\times h)\circ \alpha =(f\times g)\circ p} .

Так как является эпиморфизмом, то отсюда следует . Аналогично, используя проекцию на второй множитель, получаем и поэтому , что абсурдно. п {\displaystyle p} ф = ф × г {\displaystyle f=f\times g} г = ф × г {\displaystyle g=f\times g} ф = г {\displaystyle f=g}

Доказательство

Условие когерентности (Моноидальная категория)

В моноидальной категории следующие два условия называются условиями когерентности : С {\displaystyle С}

α А , Б , С : ( А ⊗ Б ) ⊗ С → А ⊗ ( Б ⊗ С ) {\displaystyle \alpha _{A,B,C}\colon (A\otimes B)\otimes C\rightarrow A\otimes (B\otimes C)}
  • Кроме того, пусть тождественный объект и имеет левое тождество, естественный изоморфизм, называемый левым унитором : я {\displaystyle Я} я {\displaystyle Я} λ А {\displaystyle \лямбда _{A}}
λ А : я ⊗ А → А {\displaystyle \lambda _{A}:I\otimes A\rightarrow A}
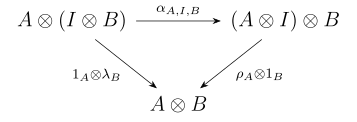
а также, пусть имеет правую единицу, естественный изоморфизм, называемый правой единицей : я {\displaystyle Я} ρ А {\displaystyle \rho _{A}}
ρ А : А ⊗ я → А {\displaystyle \rho _{A}:A\otimes I\rightarrow A} .

Пятиугольник и треугольная идентичность

Чтобы удовлетворить условию когерентности, достаточно доказать только тождество пятиугольника и треугольника, что по сути совпадает с тем, что утверждается в статье Келли (1964). [5]

Смотрите также

Примечания

  1. ^ Мак Лейн 1998, Глава VII, § 2.
  2. ^ Келли 1974, 1.2
  3. ^ Шауэнбург 2001
  4. ↑ Mac Lane 1998, Гл. VII. конец § 1.
  5. ^ Келли 1964

Ссылки

  • Келли, GM (1964). «Об условиях Маклейна для согласованности естественных ассоциативностей, коммутативностей и т. д.». Журнал алгебры . 1 (4): 397– 402. doi :10.1016/0021-8693(64)90018-3.
  • Хасегава, Масахито (2009). «О прослеживаемых моноидальных замкнутых категориях». Математические структуры в информатике . 19 (2): 217– 244. doi :10.1017/S0960129508007184.
  • Джоял, А.; Стрит , Р. (1993). «Сплетенные тензорные категории». Успехи в математике . 102 (1): 20–78 . doi : 10.1006/aima.1993.1055 .
  • Маклейн, Сондерс (октябрь 1963 г.). «Естественная ассоциативность и коммутативность». Брошюра Института Райса — Исследования Университета Райса . hdl :1911/62865.
  • Маклейн, Сондерс (1965). «Категориальная алгебра». Бюллетень Американского математического общества . 71 (1): 40– 106. doi : 10.1090/S0002-9904-1965-11234-4 .
  • Mac Lane, Saunders (1998). Категории для работающего математика. Нью-Йорк: Springer. ISBN 0-387-98403-8. OCLC  37928530.
  • Раздел 5 Saunders Mac Lane, Mac Lane, Saunders (1976). «Топология и логика как источник алгебры». Бюллетень Американского математического общества . 82 (1): 1– 40. doi : 10.1090/S0002-9904-1976-13928-6 .
  • Шауенбург, Питер (2001). «Превращение моноидальных категорий в строгие». The New York Journal of Mathematics [Только в электронном виде] . 7 : 257–265 . ISSN  1076-9803.

Дальнейшее чтение

  • Келли, GM (1974). "Теоремы когерентности для нестрогих алгебр и для дистрибутивных законов". Категория Семинар . Заметки лекций по математике. Том 420. С.  281– 375. doi :10.1007/BFb0063106. ISBN 978-3-540-06966-9.
  • Армстронг, Джон (29 июня 2007 г.). «Теорема когерентности Маклейна». Математик, не знающий оправданий .
  • Этингоф, Павел; Гелаки, Шломо; Никшич, Дмитрий; Острик, Виктор. "18.769, Весна 2009, Темы выпускных курсов по теории лжи: Тензорные категории §.Лекция 3". MIT Open Course Ware .
  • "теорема согласованности для моноидальных категорий". ncatlab.org .
  • «Доказательство Маклейна теоремы о когерентности для моноидальных категорий». ncatlab.org .
  • "согласованность и строгость". ncatlab.org .
  • "согласованность и строгость для моноидальных категорий". ncatlab.org .
  • "Пентагональная идентичность". ncatlab.org .
Значок заглушки

Эта статья по теории категорий — заглушка . Вы можете помочь Википедии, расширив ее.

Получено с "https://en.wikipedia.org/w/index.php?title=Теорема_когерентности_Мак-Лейна&oldid=1266985328"