Световое поле
Световое поле , или световое поле , — это векторная функция , описывающая количество света, текущего в каждом направлении через каждую точку пространства. Пространство всех возможных световых лучей задается пятимерной пленоптической функцией , а величина каждого луча задается его яркостью . Майкл Фарадей был первым, кто предположил, что свет следует интерпретировать как поле, во многом похожее на магнитные поля, над которыми он работал. [1] Термин световое поле был придуман Андреем Гершуном в классической статье 1936 года о радиометрических свойствах света в трехмерном пространстве.
Термин «поле сияния» может также использоваться для обозначения схожих или идентичных [2] концепций. Термин используется в современных исследованиях, таких как нейронные поля сияния
Пленоптическую функцию
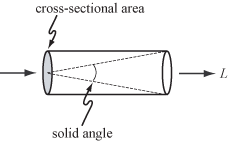
Для геометрической оптики — т. е. для некогерентного света и для объектов, больших, чем длина волны света — основным носителем света является луч . Мерой количества света, проходящего вдоль луча, является яркость , обозначаемая L и измеряемая в Вт·ср −1 ·м −2 ; т. е. ватты (Вт) на стерадиан (ср) на квадратный метр (м 2 ). Стерадианы являются мерой телесного угла , а квадратные метры используются в качестве меры площади поперечного сечения, как показано справа.

Яркость вдоль всех таких лучей в области трехмерного пространства, освещенной неизменным расположением источников света, называется пленоптической функцией. [3] Пленоптическая функция освещенности — это идеализированная функция, используемая в компьютерном зрении и компьютерной графике для выражения изображения сцены из любой возможной позиции просмотра под любым углом обзора в любой момент времени. Она не используется на практике в вычислениях, но концептуально полезна для понимания других концепций в зрении и графике. [4] Поскольку лучи в пространстве могут быть параметризованы тремя координатами x , y и z и двумя углами θ и ϕ , как показано слева, это пятимерная функция, то есть функция над пятимерным многообразием, эквивалентная произведению трехмерного евклидова пространства и 2-сферы .
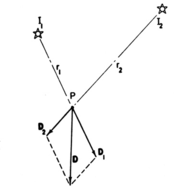
Световое поле в каждой точке пространства можно рассматривать как бесконечный набор векторов, по одному на каждое направление, падающее на точку, с длинами, пропорциональными их яркостям.
Интеграция этих векторов по любому набору источников света или по всей сфере направлений дает одно скалярное значение — общую освещенность в этой точке и результирующее направление. На рисунке показан этот расчет для случая двух источников света. В компьютерной графике эта векторная функция трехмерного пространства называется векторным полем освещенности. [6] Направление вектора в каждой точке поля можно интерпретировать как ориентацию плоской поверхности, размещенной в этой точке, чтобы наиболее ярко ее осветить.
Более высокая размерность
Время, длину волны и угол поляризации можно рассматривать как дополнительные измерения, соответственно получая более многомерные функции.
4D световое поле

В пленоптической функции, если область интереса содержит вогнутый объект (например, сложенную чашей ладонь), то свет, покидающий одну точку на объекте, может пройти лишь небольшое расстояние, прежде чем другая точка на объекте заблокирует его. Ни одно практическое устройство не может измерить функцию в такой области.
Однако для мест за пределами выпуклой оболочки объекта (например, термоусадочная пленка) пленоптическую функцию можно измерить, захватив несколько изображений. В этом случае функция содержит избыточную информацию, поскольку яркость вдоль луча остается постоянной по всей его длине. Избыточная информация представляет собой ровно одно измерение, оставляя четырехмерную функцию, называемую по-разному фотическим полем, четырехмерным световым полем [7] или люмиграфом. [8] Формально поле определяется как яркость вдоль лучей в пустом пространстве.
Набор лучей в световом поле может быть параметризован различными способами. Наиболее распространенным является двухплоскостная параметризация. Хотя эта параметризация не может представлять все лучи, например лучи, параллельные двум плоскостям, если плоскости параллельны друг другу, она тесно связана с аналитической геометрией перспективного изображения. Простой способ думать о двухплоскостном световом поле — это как о наборе перспективных изображений плоскости st (и любых объектов, которые могут лежать по обе стороны от нее или за ней), каждое из которых получено с позиции наблюдателя на плоскости uv . Световое поле, параметризованное таким образом, иногда называют световой пластиной.

Звук аналоговый
Аналогом 4D светового поля для звука является звуковое поле или волновое поле , как в синтезе волнового поля , а соответствующая параметризация — интеграл Кирхгофа–Гельмгольца , который утверждает, что при отсутствии препятствий звуковое поле с течением времени задается давлением на плоскость. Таким образом, это два измерения информации в любой момент времени, а с течением времени — трехмерное поле.
Эта двумерность, по сравнению с кажущейся четырехмерностью света, объясняется тем, что свет распространяется лучами (0D в момент времени, 1D с течением времени), в то время как по принципу Гюйгенса-Френеля фронт звуковой волны можно смоделировать как сферические волны (2D в момент времени, 3D с течением времени): свет движется в одном направлении (2D информации), в то время как звук распространяется во всех направлениях. Однако свет, распространяющийся в невакуумных средах, может рассеиваться аналогичным образом, и необратимость или потеря информации при рассеянии заметны в кажущейся потере системного измерения.
Перефокусировка изображения
Поскольку световое поле предоставляет пространственную и угловую информацию, мы можем изменить положение фокальных плоскостей после экспозиции, что часто называют перефокусировкой . Принцип перефокусировки заключается в получении обычных 2-D фотографий из светового поля посредством интегрального преобразования. Преобразование принимает световое поле в качестве входных данных и генерирует фотографию, сфокусированную на определенной плоскости.
Предполагая, что представляет собой 4-мерное световое поле, которое регистрирует световые лучи, проходящие из положения на первой плоскости в положение на второй плоскости, где — расстояние между двумя плоскостями, 2-мерную фотографию на любой глубине можно получить с помощью следующего интегрального преобразования: [9]
- ,
или более кратко,
- ,
где , , а — оператор фотографии.
На практике эта формула не может быть использована напрямую, поскольку пленоптическая камера обычно захватывает дискретные образцы светового поля , и, следовательно, для вычисления требуется повторная выборка (или интерполяция) . Другая проблема — высокая сложность вычислений. Для вычисления 2-D фотографии из 4-D светового поля сложность формулы составляет . [9]
Фотография среза Фурье
Одним из способов снижения сложности вычислений является принятие концепции теоремы о срезе Фурье : [9] Оператор фотографии можно рассматривать как сдвиг, за которым следует проекция. Результат должен быть пропорционален расширенному 2-мерному срезу 4-мерного преобразования Фурье светового поля. Точнее, перефокусированное изображение может быть получено из 4-мерного спектра Фурье светового поля путем извлечения 2-мерного среза, применения обратного 2-мерного преобразования и масштабирования. Асимптотическая сложность алгоритма составляет .
Дискретное преобразование стека фокусов
Другой способ эффективного вычисления 2-D фотографий — это использование дискретного преобразования фокусного стека (DFST). [10] DFST предназначен для создания коллекции перефокусированных 2-D фотографий, или так называемого Focal Stack . Этот метод может быть реализован с помощью быстрого дробного преобразования Фурье (FrFT).
Оператор дискретной фотографии определяется следующим образом для светового поля, выбранного в 4-мерной сетке :
Поскольку DFST обычно не находится на четырехмерной сетке, для вычисления значений, не относящихся к сетке, он применяет тригонометрическую интерполяцию .
Алгоритм состоит из следующих шагов:
- Выполняем выборку светового поля с периодом выборки и получаем дискретизированное световое поле .
- Дополните сигнал нулями так, чтобы длина сигнала была достаточной для FrFT без наложения спектров.
- Для каждого вычислите дискретное преобразование Фурье и получите результат .
- Для каждого фокусного расстояния вычислите дробное преобразование Фурье , где порядок преобразования зависит от , и получите результат .
- Вычислите обратное дискретное преобразование Фурье для .
- Удалите пограничные пиксели, чтобы каждая 2-D фотография имела размер
Методы создания световых полей
В компьютерной графике световые поля обычно создаются либо путем рендеринга 3D-модели , либо путем фотографирования реальной сцены. В любом случае, чтобы создать световое поле, необходимо получить виды для большого набора точек обзора. В зависимости от параметризации этот набор обычно охватывает некоторую часть линии, круга, плоскости, сферы или другой формы, хотя возможны и неструктурированные наборы. [11]
Устройства для фотографической фиксации световых полей могут включать в себя движущуюся ручную камеру или роботизированную камеру, [12] дугу камер (как в эффекте пули времени, используемом в «Матрице» ), плотный массив камер, [13] ручные камеры , [14] [15] микроскопы, [16] или другую оптическую систему. [17]
Количество изображений в световом поле зависит от приложения. Захват светового поля статуи Ночи Микеланджело [18] содержит 24 000 1,3-мегапиксельных изображений, что считается большим по состоянию на 2022 год. Для того чтобы рендеринг светового поля полностью захватил непрозрачный объект, изображения должны быть сделаны как минимум спереди и сзади. Менее очевидно, что для объекта, который лежит по обе стороны плоскости st , мелко разнесенные изображения должны быть сделаны на плоскости uv (в двухплоскостной параметризации, показанной выше).
Количество и расположение изображений в световом поле, а также разрешение каждого изображения вместе называются «выборкой» 4D светового поля. [19] Также интерес представляют эффекты окклюзии, [20] освещения и отражения. [21]
Приложения

Светотехника
Причиной изучения Гершуном светового поля было получение (в замкнутой форме) схем освещения, которые можно было бы наблюдать на поверхностях из-за источников света различной формы, расположенных над этими поверхностями. [23] Раздел оптики, посвященный светотехнике, называется неизображающей оптикой . [24] Она широко использует концепцию линий потока (линий потока Гершуна) и векторного потока (светового вектора Гершуна). Однако световое поле (в данном случае положения и направления, определяющие световые лучи) обычно описывается в терминах фазового пространства и гамильтоновой оптики .
Рендеринг светового поля
Извлечение соответствующих 2D-срезов из 4D-светового поля сцены позволяет получить новые виды сцены. [25] В зависимости от параметризации светового поля и срезов эти виды могут быть перспективными , ортографическими , скрещенно-щелевыми, [26] общими линейными камерами, [27] многоперспективными, [28] или другим типом проекции. Рендеринг светового поля является одной из форм рендеринга на основе изображений .
Синтетическая апертура фотографии
Интеграция соответствующего 4D подмножества образцов в световом поле может аппроксимировать вид, который будет захвачен камерой с конечной (т. е. не пинхол ) апертурой. Такой вид имеет конечную глубину резкости . Сдвиг или деформация светового поля перед выполнением этой интеграции может фокусироваться на различных фронтально-параллельных [29] или наклонных [30] плоскостях. Изображения, захваченные цифровыми камерами, которые захватывают световое поле [14], могут быть перефокусированы.
3D-дисплей
Представление светового поля с использованием технологии, которая сопоставляет каждый образец с соответствующим лучом в физическом пространстве, создает автостереоскопический визуальный эффект, схожий с просмотром исходной сцены. Нецифровые технологии для этого включают интегральную фотографию , панорамограммы параллакса и голографию ; цифровые технологии включают размещение массива линз на экране дисплея с высоким разрешением или проецирование изображения на массив линз с помощью массива видеопроекторов. Массив видеокамер может захватывать и отображать изменяющееся во времени световое поле. По сути, это представляет собой систему 3D-телевидения . [31] Современные подходы к отображению светового поля изучают совместные конструкции оптических элементов и компрессионные вычисления для достижения более высоких разрешений, повышенной контрастности, более широких полей зрения и других преимуществ. [32]
Визуализация мозга
Нейронная активность может быть зарегистрирована оптически путем генетического кодирования нейронов с помощью обратимых флуоресцентных маркеров, таких как GCaMP , которые указывают на присутствие ионов кальция в реальном времени. Поскольку микроскопия светового поля захватывает полную объемную информацию в одном кадре, можно контролировать нейронную активность в отдельных нейронах, случайно распределенных в большом объеме с частотой видеокадров. [33] Количественное измерение нейронной активности может быть выполнено, несмотря на оптические аберрации в мозговой ткани и без реконструкции объемного изображения, [34] и может использоваться для контроля активности в тысячах нейронов. [35]
Обобщенная реконструкция сцены (GSR)
Это метод 3D-реконструкции из нескольких изображений , который создает модель сцены, включающую обобщенное световое поле и повторно освещаемое поле материи. [36] Обобщенное световое поле представляет свет, текущий в каждом направлении через каждую точку поля. Повторно освещаемое поле материи представляет свойства взаимодействия света и излучательную способность материи, занимающей каждую точку поля. Структуры данных сцены могут быть реализованы с использованием нейронных сетей, [37] [38] [39] и структур на основе физики, [40] [41] среди прочих. [36] Световые и материальные поля по крайней мере частично распутаны. [36] [42]
Голографические стереограммы
Генерация изображений и предыскажение синтетических изображений для голографических стереограмм являются одними из самых ранних примеров вычисляемых световых полей. [43]
Уменьшение бликов
Блики возникают из-за многократного рассеивания света внутри корпуса камеры и оптики объектива, что снижает контрастность изображения. Хотя блики были проанализированы в пространстве изображений 2D, [44] полезно идентифицировать их как явление пространства лучей 4D. [45] Статистический анализ пространства лучей внутри камеры позволяет классифицировать и удалять артефакты бликов. В пространстве лучей блики ведут себя как высокочастотный шум и могут быть уменьшены путем отбрасывания выбросов. Такой анализ может быть выполнен путем захвата светового поля внутри камеры, но это приводит к потере пространственного разрешения. Равномерная и неравномерная выборка лучей может использоваться для уменьшения бликов без существенного ухудшения разрешения изображения. [45]
Смотрите также
- Чувствительный к углу пиксель
- Двойная фотография
- Камера светового поля
- Литро
- Рэйтрикс
- Отражательная бумага
Примечания
- ↑ Фарадей, Майкл (30 апреля 2009 г.). «LIV. Размышления о лучевых вибрациях». Philosophical Magazine . Серия 3. 28 (188): 345–350. doi :10.1080/14786444608645431. Архивировано из оригинала 2013-02-18.
- ^ https://arxiv.org/pdf/2003.08934.pdf [ пустой URL-адрес PDF ]
- ^ Адельсон 1991
- ^ Вонг 2002
- ^ Гершун, рис. 17
- ^ Арво, 1994
- ^ Левой 1996
- ^ Гортлер 1996
- ^ abc Ng, Ren (2005). "Фурье-фотография". ACM SIGGRAPH 2005 Papers . Нью-Йорк, Нью-Йорк, США: ACM Press. стр. 735–744. doi :10.1145/1186822.1073256. ISBN 9781450378253. S2CID 1806641.
- ^ Нава, Ф. Перес; Маричал-Эрнандес, JG; Родригес-Рамос, JM (август 2008 г.). «Дискретное фокальное стек-преобразование». 2008 16-я Европейская конференция по обработке сигналов : 1–5.
- ^ Бюлер 2001
- ^ Левой 2002
- ^ Канада 1998; Ян 2002; Уилберн 2005 г.
- ^ ab Ng 2005
- ^ Георгиев 2006; Марва 2013
- ^ Левой 2006
- ^ Боллес 1987
- ^ "Световое поле статуи Ночи Микеланджело". accademia.stanford.edu . Получено 2022-02-08 .
- ^ Чай (2000)
- ^ Дюран (2005)
- ^ Рамамурти (2006)
- ^ Гершун, рис. 24
- ^ Эшдаун 1993
- ^ Чавес 2015; Уинстон 2005
- ^ Левой 1996; Гортлер 1996
- ^ Зомет 2003
- ^ Ю и Макмиллан 2004
- ^ Радемахер 1998
- ^ Исаксен 2000
- ^ Вайш 2005
- ^ Джавиди 2002; Матусик 2004
- ^ Вецштейн 2012, 2011; Ланман 2011, 2010
- ^ Гросеник, 2009, 2017; Перес, 2015 г.
- ^ Пегард, 2016
- ^ Гросеник, 2017
- ^ abc Леффингвелл, 2018
- ^ Милденхолл, 2020
- ^ Руднев, Виктор; Элгариб, Мохамед; Смит, Уильям; Лю, Линцзе; Голяник, Владислав; Теобальт, Кристиан (21 июля 2022 г.). «NeRF для повторного освещения наружных сцен». Европейская конференция по компьютерному зрению (ECCV) 2022 : 1–22. arXiv : 2112.05140 .
- ^ Шринивасан, Пратуаль; Дэн, Боян; Чжан, Сюмин; Танчик, Мэтью; Милденхолл, Бен; Баррон, Джонатан (7 декабря 2020 г.). «NeRV: нейронное отражение и поля видимости для повторного освещения и синтеза представлений». CVPR : 1–12. arXiv : 2012.03927 .
- ^ Ю и Фридович-Кейл, 2021
- ^ Кербл, Бернхард; Копанас, Георгиос; Леймкюлер, Томас; Дреттакис, Джордж (08.08.2023). «3D-гауссовское разбрызгивание для визуализации поля излучения в реальном времени». arXiv : 2308.04079 [cs.GR].
- ^ Чжан, Цзиньян; Яо, Яо; Ли, Шивэй; Лю, Цзинбо; Фан, Тянь; Маккиннон, Дэвид; Цинь, Янхай; Цюань, Лонг (30 марта 2023 г.). «NeILF++: Inter-Reflectable Light Fields for Geometry and Material Estimation». стр. 1–5. arXiv : 2303.17147 [cs.CV].
- ^ Галле 1991, 1994
- ^ Талвала 2007
- ^ ab Raskar 2008
Ссылки
Теория
- Адельсон, Э. Х., Берген, Дж. Р. (1991). «Пленоптическая функция и элементы раннего зрения», в книге «Вычислительные модели визуальной обработки » , под ред. М. Ланди и Дж. А. Мовшона, MIT Press, Кембридж, 1991, стр. 3–20.
- Арво, Дж. (1994). «Якобиан излучения для частично закрытых многогранных источников», Proc. ACM SIGGRAPH , ACM Press, стр. 335–342.
- Боллз, Р. К., Бейкер, Х. Х., Маримонт, Д. Х. (1987). «Анализ изображений в эпиполярной плоскости: подход к определению структуры по движению», Международный журнал компьютерного зрения , том 1, № 1, 1987, Kluwer Academic Publishers, стр. 7–55.
- Фарадей, М., «Мысли о лучевых колебаниях», Philosophical Magazine , S.3, Vol XXVIII, N188, май 1846 г.
- Гершун, А. (1936). «Световое поле», Москва, 1936. Перевод П. Муна и Г. Тимошенко в Journal of Mathematics and Physics , т. XVIII, MIT, 1939, стр. 51–151.
- Гортлер, С. Дж., Гжещук, Р., Селиски, Р., Коэн, М. (1996). «Люмиграф», Proc. ACM SIGGRAPH , ACM Press, стр. 43–54.
- Левой, М., Ханрахан, П. (1996). «Рендеринг светового поля», Proc. ACM SIGGRAPH , ACM Press, стр. 31–42.
- Мун, П., Спенсер, Д. Э. (1981). Фотическое поле , MIT Press.
- Вонг, ТТ, Фу, ЧВ, Хенг, ПА, Леунг ЧС (2002). «Функция пленоптического освещения», IEEE Trans. Multimedia , том 4, № 3, стр. 361–371.
Анализ
- G. Wetzstein, I. Ihrke, W. Heidrich (2013) «О пленоптическом мультиплексировании и реконструкции», Международный журнал компьютерного зрения (IJCV) , том 101, выпуск 2, стр. 384–400.
- Рамамурти, Р., Махаджан, Д., Белхумер, П. (2006). «Анализ первого порядка освещения, затенения и теней», ACM TOG .
- Цвикер, М., Матусик, В., Дюран, Ф., Пфистер, Х. (2006). «Сглаживание для автомультископических 3D-дисплеев», симпозиум Eurographics по рендерингу, 2006 .
- Нг, Р. (2005). «Фурье-фотография», Proc. ACM SIGGRAPH , ACM Press, стр. 735–744.
- Дюран, Ф., Хольцшух, Н., Солер, К., Чан, Э., Силлион, Ф. К. (2005). «Частотный анализ переноса света», Proc. ACM SIGGRAPH , ACM Press, стр. 1115–1126.
- Чай, Дж.-Х., Тонг, Х., Чан, С.-К., Шум, Х. (2000). «Пленоптический отбор проб», Proc. ACM SIGGRAPH , ACM Press, стр. 307–318.
- Халле, М. (1994) «Голографические стереограммы как дискретные системы формирования изображений» [ постоянная неработающая ссылка ] , в SPIE Proc. Vol. #2176: Практическая голография VIII , под ред. С.А. Бентона, стр. 73–84.
- Ю, Дж., Макмиллан, Л. (2004). «Общие линейные камеры», Proc. ECCV 2004 , Lecture Notes in Computer Science, стр. 14–27.
Камеры
- Марва, К., Вецштейн, Г., Бандо, Й., Раскар, Р. (2013). «Компрессионная фотография светового поля с использованием сверхполных словарей и оптимизированных проекций», ACM Transactions on Graphics (SIGGRAPH) .
- Liang, CK, Lin, TH, Wong, BY, Liu, C., Chen, HH (2008). «Фотография с программируемой апертурой: получение мультиплексного светового поля», Proc. ACM SIGGRAPH .
- Вирарагхаван, А., Раскар, Р., Агравал, А., Мохан, А., Тамблин, Дж. (2007). «Пятнистая фотография: камеры с улучшенной маской для гетеродинированных световых полей и перефокусировки кодированной апертуры», Proc. ACM SIGGRAPH .
- Георгиев, Т., Чжэн, Ч., Наяр, С., Кёрлесс, Б., Салезин, Д., Интвала, Ч. (2006). «Компромиссы пространственно-углового разрешения в интегральной фотографии», Proc. EGSR 2006 .
- Канаде, Т., Сайто, Х., Ведула, С. (1998). «3D-комната: оцифровка изменяющихся во времени 3D-событий с помощью синхронизированных нескольких видеопотоков», технический отчет CMU-RI-TR-98-34, декабрь 1998 г.
- Левой, М. (2002). Стэнфордский сферический портал.
- Левой, М., Нг, Р., Адамс, А., Футер, М., Хоровиц, М. (2006). «Микроскопия светового поля», ACM Transactions on Graphics (Proc. SIGGRAPH), том 25, № 3.
- Нг, Р., Левой, М., Бредиф, М., Дюваль, Г., Хоровиц, М., Ханрахан, П. (2005). «Фотография светового поля с помощью ручной пленоптической камеры», Stanford Tech Report CTSR 2005–02, апрель 2005 г.
- Wilburn, B., Joshi, N., Vaish, V., Talvala, E., Antunez, E., Barth, A., Adams, A., Levoy, M., Horowitz, M. (2005). «Высокопроизводительная обработка изображений с использованием больших массивов камер», ACM Transactions on Graphics (Proc. SIGGRAPH), том 24, № 3, стр. 765–776.
- Янг, Дж. К., Эверетт, М., Бюлер, К., Макмиллан, Л. (2002). «Распределенная камера светового поля в реальном времени», Труды семинара по рендерингу Eurographics 2002 .
- «Камера CAFADIS»
Дисплеи
- Вецштейн, Г., Ланман, Д., Хирш, М., Раскар, Р. (2012). «Тензорные дисплеи: компрессионный дисплей светового поля с использованием многослойных дисплеев с направленной подсветкой», ACM Transactions on Graphics (SIGGRAPH)
- Вецштейн, Г., Ланман, Д., Хайдрих, В., Раскар, Р. (2011). «Слоистый 3D: томографический синтез изображений для светового поля на основе затухания и дисплеев с высоким динамическим диапазоном», ACM Transactions on Graphics (SIGGRAPH)
- Ланман, Д., Вецштейн, Г., Хирш, М., Хайдрих, В., Раскар, Р. (2011). «Поля поляризации: отображение динамического светового поля с использованием многослойных ЖК-дисплеев», ACM Transactions on Graphics (SIGGRAPH Asia)
- Ланман, Д., Хирш, М. Ким, Й., Раскар, Р. (2010). «HR3D: 3D-дисплей без очков с использованием двухслойных ЖК-дисплеев. Высококачественный 3D-дисплей с использованием адаптивных к контенту параллаксных барьеров», ACM Transactions on Graphics (SIGGRAPH Asia)
- Матусик, В., Пфистер, Х. (2004). «3D-телевидение: масштабируемая система для получения, передачи и автостереоскопического отображения динамических сцен в реальном времени», Proc. ACM SIGGRAPH , ACM Press.
- Джавиди, Б., Окано, Ф., ред. (2002). Трехмерное телевидение, видео и технологии отображения , Springer-Verlag.
- Klug, M., Burnett, T., Fancello, A., Heath, A., Gardner, K., O'Connell, S., Newswanger, C. (2013). «Масштабируемая, совместная, интерактивная система отображения светового поля», SID Symposium Digest of Technical Papers
- Fattal, D., Peng, Z., Tran, T., Vo, S., Fiorentino, M., Brug, J., Beausoleil, R. (2013). «Многонаправленная подсветка для широкоугольного трехмерного дисплея без очков», Nature 495, 348–351
Архивы
- «Архив Стэнфордского светового поля»
- «Репозиторий светового поля UCSD/MERL»
- «Тест светового поля HCI»
- «Архив синтетического светового поля»
Приложения
- Гросеник, Л., Андерсон, Т., Смит С.Дж. (2009) «Выбор упругого источника для визуализации нейронных ансамблей in vivo». От нано до макро, 6-й Международный симпозиум IEEE по биомедицинской визуализации. (2009) 1263–1266.
- Grosenick, L., Broxton, M., Kim, CK, Liston, C., Poole, B., Yang, S., Andalman, A., Scharff, E., Cohen, N., Yizhar, O., Ramakrishnan, C., Ganguli, S., Suppes, P., Levoy, M., Deisseroth, K. (2017) «Идентификация динамики клеточной активности в больших объемах тканей мозга млекопитающих» bioRxiv 132688; doi: Идентификация динамики клеточной активности в больших объемах тканей мозга млекопитающих.
- Хайде, Ф., Вецштейн, Г., Раскар, Р., Хайдрих, В. (2013) «Адаптивный синтез изображений для компрессионных дисплеев», ACM Transactions on Graphics (SIGGRAPH)
- Вецштейн, Г., Раскар, Р., Хайдрих, В. (2011) «Ручная шлирен-фотография с зондами светового поля», Международная конференция IEEE по вычислительной фотографии (ICCP)
- Перес, Ф., Маричал, Дж. Г., Родригес, Дж. М. (2008). «Дискретное фокальное стековое преобразование», Proc. EUSIPCO
- Раскар, Р., Агравал, А., Уилсон, К., Вирарагхаван, А. (2008). «Фотография с учетом бликов: 4D-выборка лучей для уменьшения эффекта бликов объективов камеры», Proc. ACM SIGGRAPH.
- Талвала, Э.В., Адамс, А., Горовиц, М., Левой, М. (2007). «Вуалирующий блик в изображениях с высоким динамическим диапазоном», Proc. ACM SIGGRAPH.
- Халле, М., Бентон, С., Клуг, М., Андеркоффлер, Дж. (1991). «Ультраграмма: обобщенная голографическая стереограмма» [ постоянная мертвая ссылка ] , SPIE т. 1461, Практическая голография V , под ред. С. А. Бентона, стр. 142–155.
- Зомет, А., Фельдман, Д., Пелег, С., Вайншолл, Д. (2003). «Мозаика новых представлений: проекция скрещенных щелей», Труды IEEE по анализу образов и машинному интеллекту (PAMI) , том 25, № 6, июнь 2003 г., стр. 741–754.
- Vaish, V., Garg, G., Talvala, E., Antunez, E., Wilburn, B., Horowitz, M., Levoy, M. (2005). «Фокусировка с помощью синтезированной апертуры с использованием факторизации сдвига-деформации преобразования просмотра», Proc. Workshop on Advanced 3D Imaging for Safety and Security , совместно с CVPR 2005.
- Бедард, Н., Шоп, Т., Хоберман, А., Харалам, МА, Шайх, Н., Ковачевич, Й., Балрам, Н., Тошич, И. (2016). «Конструкция отоскопа светового поля для трехмерной визуализации среднего уха in vivo». Biomedical optics express , 8 (1), стр. 260–272.
- Кариджанни, С., Мартинелло, М., Спинулас, Л., Фроссар, П., Тосич, И. (2018). «Автоматизированная регистрация барабанной перепонки по данным светового поля». Международная конференция IEEE по обработке изображений (ICIP)
- Радемахер, П., Бишоп, Г. (1998). «Изображения с несколькими центрами проекции», Proc. ACM SIGGRAPH , ACM Press.
- Исаксен, А., Макмиллан, Л., Гортлер, С.Дж. (2000). «Динамически репараметризованные световые поля», Proc. ACM SIGGRAPH , ACM Press, стр. 297–306.
- Бюлер, К., Боссе, М., Макмиллан, Л., Гортлер, С., Коэн, М. (2001). «Неструктурированная визуализация люмиграфа», Proc. ACM SIGGRAPH , ACM Press.
- Эшдаун, И. (1993). «Фотометрия ближнего поля: новый подход», Журнал общества инженеров-светотехников , т. 22, № 1, зима, 1993, стр. 163–180.
- Чавес, Дж. (2015) «Введение в невизуализирующую оптику, второе издание», CRC Press
- Уинстон Р., Миньяно Дж. К., Бенитес П. Г., Шац Н., Борц Дж. К. (2005) «Оптика без изображения», Academic Press
- Pégard, NC, Liu HY, Antipa, N., Gerlock M., Adesnik, H. и Waller, L.. Компрессионная микроскопия светового поля для трехмерной регистрации нейронной активности. Optica 3, № 5, стр. 517–524 (2016).
- Леффингвелл, Дж., Мигер, Д., Махмуд, К., Акерсон, С. (2018). «Обобщенная реконструкция сцены». arXiv:1803.08496v3 [cs.CV], стр. 1–13.
- Милденхолл, Б., Шринивасан, П.П., Танчик, М., Баррон, Дж.Т., Рамамурти, Р. и Нг, Р. (2020). «NeRF: Представление сцен как нейронных полей излучения для синтеза вида». Компьютерное зрение – ECCV 2020, 405–421.
- Ю, А., Фридович-Кейл, С., Танчик, М., Чен, К., Рехт, Б., Каназава, А. (2021). «Пленоксели: поля излучения без нейронных сетей». arXiv:2111.11215, стр. 1–25
- Перес, CC; Лаури, A; и др. (сентябрь 2015 г.). «Нейровизуализация кальция у личинок данио-рерио с использованием готовой к использованию камеры светового поля». Журнал биомедицинской оптики . 20 (9): 096009. Bibcode : 2015JBO....20i6009C. doi : 10.1117/1.JBO.20.9.096009 . PMID 26358822.
- Перес, CC, Лаури, A., Симвулидис, P., Каппетта, M., Эрдманн, A. и Вестмейер, GG (2015). Нейровизуализация кальция у личинок данио-рерио с использованием готовой к использованию камеры светового поля. Журнал биомедицинской оптики, 20(9), 096009-096009.
- Леон, К., Гальвис, Л. и Аргуэльо, Х. (2016). «Реконструкция многоспектрального светового поля (пленоптическая функция 5d) на основе компрессионного зондирования с цветными кодированными апертурами из 2D-проекций» Revista Facultad de Ingeniería Universidad de Antioquia 80, стр. 131.





={1 \over \alpha ^{2}F^{2}}\iint L_{F}\left(u\left(1-{\frac {1}{\alpha }}\right)+{\frac {s}{\alpha }},v\left(1-{\frac {1}{\alpha }}\right)+{\frac {t}{\alpha }},u,v\right)~dudv}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60adeb0f381818bb17973638d56bce280c6c4ffe)
={\frac {1}{\alpha ^{2}F^{2}}}\int L_{F}\left({\boldsymbol {u}}\left(1-{\frac {1}{\alpha }}\right)+{\frac {\boldsymbol {s}}{\alpha }},{\boldsymbol {u}}\right)d{\boldsymbol {u}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93ee275f5a3c4e0535d9a48a10034709fcb261ad)


![{\displaystyle {\mathcal {P}}_{\alpha }\left[\cdot \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b933f823d86642460379aaf0e72671e44822df25)









=\sum _{{\tilde {\boldsymbol {u}}}=-{\boldsymbol {n}}_{\boldsymbol {u}}}^{{\boldsymbol {n}}_{\boldsymbol {u}}}L({\boldsymbol {u}}q+{\boldsymbol {s}},{\boldsymbol {u}})\Delta {\boldsymbol {u}},\quad \Delta {\boldsymbol {u}}=\Delta u\Delta v,\quad q=\left(1-{\frac {1}{\alpha }}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/439ba309b95250b65a62b64257388b09d20ee38e)








