Коррелограмма

В анализе данных коррелограмма — это диаграмма корреляционной статистики. Например, в анализе временных рядов график выборочных автокорреляций против (временных задержек) — это автокоррелограмма . Если на график нанесена кросс-корреляция , результат называется кросс-коррелограммой . ${\displaystyle r_{h}\,}$${\displaystyle ч\,}$

Коррелограмма — это часто используемый инструмент для проверки случайности в наборе данных . Если случайный, автокорреляции должны быть близки к нулю для любых и всех разделений по времени. Если неслучайный, то одна или несколько автокорреляций будут значительно ненулевыми.

Кроме того, коррелограммы используются на этапе идентификации модели для моделей временных рядов авторегрессии Бокса–Дженкинса с скользящим средним . Автокорреляции должны быть близки к нулю для случайности; если аналитик не проверяет случайность, то обоснованность многих статистических заключений становится сомнительной. Коррелограмма является отличным способом проверки такой случайности.

В многомерном анализе корреляционные матрицы , представленные в виде цветных изображений, также могут называться «коррелограммами» или «коррграммами». ^{[1] [2] [3]}

Коррелограмма может помочь дать ответы на следующие вопросы: ^[4]

• Случайны ли данные?
• Связано ли наблюдение с соседним наблюдением?
• Связано ли наблюдение с наблюдением, удаленным дважды? (и т. д.)
• Является ли наблюдаемый временной ряд белым шумом ?
• Является ли наблюдаемый временной ряд синусоидальным?
• Является ли наблюдаемый временной ряд авторегрессионным?
• Какая модель является подходящей для наблюдаемого временного ряда?
• Это модель?

${\displaystyle Y={\text{константа}}+{\text{ошибка}}}$

действительны и достаточны?

• Верна ли формула ?${\displaystyle s_{\bar {Y}}=s/{\sqrt {N}}}$

Случайность (наряду с фиксированной моделью, фиксированной вариацией и фиксированным распределением) является одним из четырех предположений, которые обычно лежат в основе всех процессов измерения. Предположение о случайности имеет решающее значение по следующим трем причинам:

• Большинство стандартных статистических тестов зависят от случайности. Обоснованность выводов теста напрямую связана с обоснованностью предположения о случайности.
• Многие широко используемые статистические формулы основаны на предположении о случайности, наиболее распространенной из которых является формула для определения стандартной ошибки выборочного среднего:

${\displaystyle s_{\bar {Y}}=s/{\sqrt {N}}}$

где s — стандартное отклонение данных. Несмотря на широкое использование, результаты применения этой формулы не имеют никакой ценности, если предположение о случайности не выполняется.

• Для одномерных данных модель по умолчанию:

${\displaystyle Y={\text{константа}}+{\text{ошибка}}}$

Если данные не являются случайными, эта модель неверна и недействительна, а оценки параметров (таких как константа) становятся бессмысленными и недействительными.

Коэффициент автокорреляции при задержке h определяется по формуле

${\displaystyle r_{h}=c_{h}/c_{0}\,}$

где c _h — автоковариационная функция

${\displaystyle c_{h}={\frac {1}{N}}\sum _{t=1}^{Nh}\left(Y_{t}-{\bar {Y}}\right)\left(Y_{t+h}-{\bar {Y}}\right)}$

и c ₀ — функция дисперсии

${\displaystyle c_{0}={\frac {1}{N}}\sum _{t=1}^{N}\left(Y_{t}-{\bar {Y}}\right)^{2}}$

Результирующее значение r _h будет находиться в диапазоне от −1 до +1.

В некоторых источниках может использоваться следующая формула для функции автоковариации:

${\displaystyle c_{h}={\frac {1}{Nh}}\sum _{t=1}^{Nh}\left(Y_{t}-{\bar {Y}}\right)\left(Y_{t+h}-{\bar {Y}}\right)}$

Хотя это определение имеет меньше смещения , формулировка (1/ N ) имеет некоторые желательные статистические свойства и является формой, наиболее часто используемой в статистической литературе. Подробности см. на страницах 20 и 49–50 в Chatfield.

В отличие от определения выше, это определение позволяет нам вычислять немного более интуитивно. Рассмотрим пример , где для . Затем, пусть${\displaystyle c_{h}}$${\displaystyle Y_{1},\dots,Y_{N}}$${\displaystyle Y_{i}\in \mathbb {R} ^{n}}$${\displaystyle i=1,\точки ,N}$

${\displaystyle X={\begin{bmatrix}Y_{1}-{\bar {Y}}&\cdots &Y_{N}-{\bar {Y}}\end{bmatrix}}\in \mathbb {R} ^{n\times N}}$

Затем мы вычисляем матрицу Грама . Наконец, вычисляется как выборочное среднее диагонали th из . Например, диагональ th (главная диагональ) имеет элементы, а ее выборочное среднее соответствует . Диагональ st (справа от главной диагонали) имеет элементы, а ее выборочное среднее соответствует , и так далее.${\displaystyle Q=X^{\top }X}$${\displaystyle c_{h}}$${\displaystyle ч}$${\displaystyle Q}$${\displaystyle 0}$${\displaystyle Q}$${\displaystyle N}$${\displaystyle c_{0}}$${\displaystyle 1}$${\displaystyle Q}$${\displaystyle N-1}$${\displaystyle c_{1}}$

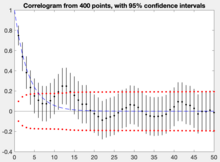
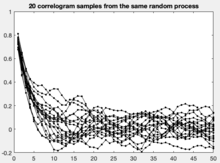
На этом же графике можно построить верхнюю и нижнюю границы автокорреляции с уровнем значимости :${\displaystyle \альфа \,}$

${\displaystyle B=\pm z_{1-\alpha /2}SE(r_{h})\,}$с предполагаемой автокорреляцией при задержке .${\displaystyle r_{h}\,}$${\displaystyle ч\,}$

Если автокорреляция выше (ниже) этой верхней (нижней) границы, нулевая гипотеза об отсутствии автокорреляции при заданном лаге и за его пределами отвергается на уровне значимости . Этот тест является приблизительным и предполагает, что временной ряд является гауссовым .${\displaystyle \альфа \,}$

В приведенном выше выражении z _{1− α /2} — это квантиль нормального распределения ; SE — это стандартная ошибка, которую можно вычислить по формуле Бартлетта для процессов MA( ℓ ):

${\displaystyle SE(r_{1})={\frac {1}{\sqrt {N}}}}$

${\displaystyle SE(r_{h})={\sqrt {\frac {1+2\sum _{i=1}^{h-1}r_{i}^{2}}{N}}}}$для${\displaystyle h>1.\,}$

В представленном примере мы можем отвергнуть нулевую гипотезу об отсутствии автокорреляции между временными точками, разделенными лагами до 4. Для большинства более длительных периодов нельзя отвергнуть нулевую гипотезу об отсутствии автокорреляции.

Обратите внимание, что существуют две различные формулы для расчета доверительных интервалов:

1. Если коррелограмма используется для проверки на случайность (т.е. на отсутствие зависимости данных от времени), рекомендуется следующая формула:

${\displaystyle \pm {\frac {z_{1-\alpha /2}}{\sqrt {N}}}}$

где N — размер выборки , z — функция квантиля стандартного нормального распределения , а α — уровень значимости . В этом случае доверительные интервалы имеют фиксированную ширину, которая зависит от размера выборки.

2. Коррелограммы также используются на этапе идентификации модели для подгонки моделей ARIMA . В этом случае для данных предполагается модель скользящего среднего , и должны быть созданы следующие доверительные интервалы:

${\displaystyle \pm z_{1-\alpha /2}{\sqrt {{\frac {1}{N}}\left(1+2\sum _{i=1}^{k}r_{i}^{2}\right)}}}$

где k — это задержка. В этом случае доверительные интервалы увеличиваются по мере увеличения задержки.

Коррелограммы доступны в большинстве статистических библиотек общего назначения.

Коррелограммы:

• питон панды : pandas.plotting.autocorrelation_plot^[5]
• R : функции acfиpacf

Коррграммы:

• питон морской : heatmap,pairplot
• Р : corrgram^{[2] [3]}

• Частичная автокорреляционная функция
• График задержки
• Спектральный график
• Сезонный подсериальный сюжет
• Масштабированная корреляция
• Вариограмма

• Ханке, Джон Э.; Райч, Артур Г.; Вихерн, Дин В. Бизнес-прогнозирование (7-е изд.). Аппер Сэддл Ривер, Нью-Джерси: Prentice Hall.
• Бокс, ГЭП; Дженкинс, Г. (1976). Анализ временных рядов: прогнозирование и контроль . Холден-Дэй.
• Чатфилд, К. (1989). Анализ временных рядов: Введение (четвертое издание). Нью-Йорк, Нью-Йорк: Chapman & Hall.

• График автокорреляции

 В статье использованы материалы, являющиеся общественным достоянием Национального института стандартов и технологий.