Арифметическая иерархия

Эта статья включает список ссылок , связанных материалов или внешних ссылок , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . Пожалуйста, помогите улучшить эту статью, введя более точные цитаты. ( Июнь 2021 г. ) ( Узнайте, как и когда удалить это сообщение )

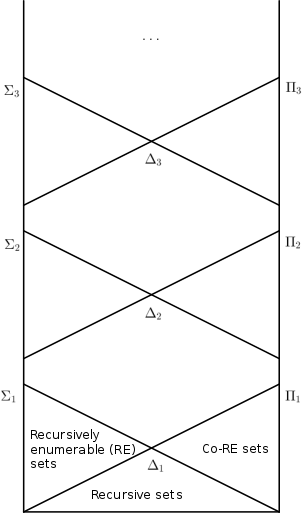
В математической логике арифметическая иерархия , арифметическая иерархия или иерархия Клини–Мостовского (в честь математиков Стивена Коула Клини и Анджея Мостовского ) классифицирует некоторые множества на основе сложности формул , которые их определяют . Любое множество, которое получает классификацию, называется арифметическим . Арифметическая иерархия была изобретена независимо Клини (1943) и Мостовским (1946). ^[1]

Арифметическая иерархия важна в теории вычислимости , эффективной дескриптивной теории множеств и изучении формальных теорий, таких как арифметика Пеано .

Алгоритм Тарского–Куратовского предоставляет простой способ получения верхней границы классификаций, присвоенных формуле и множеству, которое она определяет.

Гиперарифметическая иерархия и аналитическая иерархия расширяют арифметическую иерархию для классификации дополнительных формул и множеств.

Арифметическая иерархия присваивает классификации формулам на языке арифметики первого порядка . Классификации обозначаются и для натуральных чисел n (включая 0). Греческие буквы здесь являются символами lightface , что указывает на то, что формулы не содержат заданных параметров. ^{[ необходимо уточнение ]}${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$

Если формула логически эквивалентна формуле , не имеющей неограниченных квантификаторов, т.е. в которой все квантификаторы являются ограниченными квантификаторами , то ей присваиваются классификации и .${\displaystyle \фи}$${\displaystyle \фи}$${\displaystyle \Sigma _{0}^{0}}$${\displaystyle \Пи _{0}^{0}}$

Классификации и определяются индуктивно для каждого натурального числа n с использованием следующих правил:${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$

• Если логически эквивалентно формуле вида , где есть , то присваивается классификация .${\displaystyle \фи}$${\displaystyle \exists m_{1}\exists m_{2}\cdots \exists m_{k}\psi }$${\displaystyle \пси}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle \фи}$${\displaystyle \Сигма _{n+1}^{0}}$
• Если логически эквивалентно формуле вида , где есть , то присваивается классификация .${\displaystyle \фи}$${\displaystyle \forall m_{1}\forall m_{2}\cdots \forall m_{k}\psi }$${\displaystyle \пси}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \фи}$${\displaystyle \Pi _{n+1}^{0}}$

Формула эквивалентна формуле, которая начинается с некоторых кванторов существования и чередует серии кванторов существования и кванторов всеобщности ; в то время как формула эквивалентна формуле, которая начинается с некоторых кванторов всеобщности и чередуется аналогичным образом.${\displaystyle \Сигма _{n}^{0}}$${\displaystyle n-1}$${\displaystyle \Пи _{n}^{0}}$

Поскольку каждая формула первого порядка имеет предваренную нормальную форму , каждой формуле назначается по крайней мере одна классификация. Поскольку избыточные квантификаторы могут быть добавлены к любой формуле, как только формуле назначается классификация или ей будут назначены классификации и для каждого m > n . Таким образом, единственной соответствующей классификацией, назначенной формуле, является та, у которой наименьшее n ; все остальные классификации могут быть определены из нее.${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle \Сигма _{м}^{0}}$${\displaystyle \Пи _{м}^{0}}$

Множество X натуральных чисел определяется формулой φ на языке арифметики Пеано (язык первого порядка с символами «0» для нуля, «S» для функции следования, «+» для сложения, «×» для умножения и «=» для равенства), если элементы X являются в точности числами, удовлетворяющими φ . То есть, для всех натуральных чисел n ,

${\displaystyle n\in X\Leftrightarrow \mathbb {N} \models \varphi ({\underline {n}}),}$

где — число на языке арифметики, соответствующее . Множество определимо в арифметике первого порядка, если оно определяется некоторой формулой на языке арифметики Пеано.${\displaystyle {\underline {н}}}$${\displaystyle n}$

Каждому множеству X натуральных чисел, которое определяется в арифметике первого порядка, назначаются классификации вида , и , где — натуральное число, следующим образом. Если X определяется формулой , то X назначается классификация . Если X определяется формулой , то X назначается классификация . Если X является и тем , и другим, то назначается дополнительная классификация .${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle \Delta _ {n}^{0}}$${\displaystyle n}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle X}$${\displaystyle \Delta _ {n}^{0}}$

Обратите внимание, что редко имеет смысл говорить о формулах; первый квантификатор формулы либо экзистенциальный, либо универсальный. Таким образом, множество не обязательно определяется формулой в том смысле, что это формула, которая является как и ; скорее, существуют и формулы, которые определяют множество. Например, множество нечетных натуральных чисел определяется либо , либо .${\displaystyle \Delta _ {n}^{0}}$${\displaystyle \Delta _ {n}^{0}}$${\displaystyle \Delta _ {n}^{0}}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle n}$${\displaystyle \forall k(n\neq 2\times k)}$${\displaystyle \exists k(n=2\times k+1)}$

Параллельное определение используется для определения арифметической иерархии на конечных декартовых степенях множества натуральных чисел. Вместо формул с одной свободной переменной, для определения арифметической иерархии на множествах из k - кортежей натуральных чисел используются формулы с k свободными переменными первого порядка . Фактически они связаны с помощью функции спаривания .

Обозначению арифметической иерархии формул можно придать следующие значения.

Нижний индекс в символах и указывает на количество чередований блоков универсальных и экзистенциальных квантификаторов первого порядка, которые используются в формуле. При этом самый внешний блок является экзистенциальным в формулах и универсальным в формулах.${\displaystyle n}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$

Верхний индекс в символах , и указывает на тип объектов, по которым проводится квантификация. Объекты типа 0 — это натуральные числа, а объекты типа — это функции, которые отображают множество объектов типа в натуральные числа. Квантификация по объектам более высокого типа, таким как функции от натуральных чисел до натуральных чисел, описывается верхним индексом больше 0, как в аналитической иерархии . Верхний индекс 0 указывает на квантификаторы по числам, верхний индекс 1 будет указывать на квантификацию по функциям от чисел до чисел (объекты типа 1), верхний индекс 2 будет соответствовать квантификации по функциям, которые принимают объект типа 1 и возвращают число, и так далее.${\displaystyle 0}$${\displaystyle \Сигма _{n}^{0}}$${\displaystyle \Пи _{n}^{0}}$${\displaystyle \Delta _ {n}^{0}}$${\displaystyle я+1}$${\displaystyle я}$

• Множества чисел определяются формулой вида , где имеет только ограниченные квантификаторы. Это в точности рекурсивно перечислимые множества .${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \существует n_{1}\cdots \существует n_{k}\psi (n_{1},\ldots ,n_{k},m)}$${\displaystyle \пси}$
• Множество натуральных чисел, которые являются индексами для машин Тьюринга , вычисляющих полные функции, равно . Интуитивно, индекс попадает в это множество тогда и только тогда, когда для каждого «существует такое , что машина Тьюринга с индексом останавливается на входе после шагов». Полное доказательство показало бы, что свойство, отображенное в кавычках в предыдущем предложении, можно определить на языке арифметики Пеано с помощью формулы.${\displaystyle \Pi _{2}^{0}}$${\displaystyle e}$${\displaystyle m}$${\displaystyle s}$${\displaystyle e}$${\displaystyle m}$${\displaystyle s}$${\displaystyle \Sigma _{1}^{0}}$
• Каждое подмножество пространства Бэра или пространства Кантора является открытым множеством в обычной топологии на этом пространстве. Более того, для любого такого множества существует вычислимое перечисление чисел Гёделя базовых открытых множеств, объединение которых является исходным множеством. По этой причине множества иногда называют эффективно открытыми . Аналогично, каждое множество замкнуто, и множества иногда называют эффективно закрытыми .${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Pi _{1}^{0}}$${\displaystyle \Pi _{1}^{0}}$
• Каждое арифметическое подмножество пространства Кантора или пространства Бэра является множеством Бореля . Иерархия Lightface Borel расширяет арифметическую иерархию, включая дополнительные множества Бореля. Например, каждое подмножество пространства Кантора или Бэра является множеством , то есть множеством, которое равно пересечению счетного числа открытых множеств. Более того, каждое из этих открытых множеств является и список чисел Гёделя этих открытых множеств имеет вычислимое перечисление. Если — формула со свободной переменной множества и свободными числовыми переменными , то множество является пересечением множеств вида как пробегает множество натуральных чисел.${\displaystyle \Pi _{2}^{0}}$${\displaystyle G_{\delta }}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \phi (X,n,m)}$${\displaystyle \Sigma _{0}^{0}}$${\displaystyle X}$${\displaystyle n,m}$${\displaystyle \Pi _{2}^{0}}$${\displaystyle \{X\mid \forall n\exists m\phi (X,n,m)\}}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \{X\mid \exists m\phi (X,n,m)\}}$${\displaystyle n}$
• Формулы можно проверить, перебрав все случаи один за другим, что возможно, поскольку все их квантификаторы ограничены. Время для этого полиномиально по своим аргументам (например, полиномиально по для ); таким образом, соответствующие им проблемы принятия решений включены в E (как экспоненциально по своему числу битов). Это больше не выполняется при альтернативных определениях , которые позволяют использовать примитивные рекурсивные функции , поскольку теперь квантификаторы могут быть ограничены любой примитивной рекурсивной функцией аргументов.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle n}$${\displaystyle \varphi (n)}$${\displaystyle n}$${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$
• Формулы в соответствии с альтернативным определением, которое позволяет использовать примитивно-рекурсивные функции с ограниченными кванторами, соответствуют наборам натуральных чисел вида для примитивно-рекурсивной функции . Это связано с тем, что разрешение ограниченного квантора ничего не добавляет к определению: для примитивно-рекурсивной функции то же самое , что и то же самое, что и ; с рекурсией хода значений каждая из них может быть определена одной примитивно-рекурсивной функцией.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \{n:f(n)=0\}}$${\displaystyle f}$${\displaystyle f}$${\displaystyle \forall k<n:f(k)=0}$${\displaystyle f(0)+f(1)+...f(n)=0}$${\displaystyle \exists k<n:f(k)=0}$${\displaystyle f(0)\cdot f(1)\cdot \ldots \cdot f(n)=0}$

Точно так же, как мы можем определить, что означает для множества X быть рекурсивным относительно другого множества Y , разрешив вычислению, определяющему X, обращаться к Y как к оракулу, мы можем расширить это понятие на всю арифметическую иерархию и определить, что означает для X быть , или в Y , обозначаемых соответственно , и . Чтобы сделать это, зафиксируем множество натуральных чисел Y и добавим предикат для принадлежности Y к языку арифметики Пеано. Затем мы говорим, что X находится в , если он определен формулой в этом расширенном языке. Другими словами, X находится , если он определен формулой , позволяющей задавать вопросы о принадлежности Y . В качестве альтернативы можно рассматривать множества как те множества, которые можно построить, начиная с множеств, рекурсивных в Y , и поочередно беря объединения и пересечения этих множеств до n раз.${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Delta _{n}^{0,Y}}$${\displaystyle \Pi _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$

Например, пусть Y — множество натуральных чисел. Пусть X — множество чисел, делящихся на элемент Y . Тогда X определяется формулой , поэтому X входит в (на самом деле он входит в , поскольку мы могли бы ограничить оба квантификатора n ).${\displaystyle \phi (n)=\exists m\exists t(Y(m)\land m\times t=n)}$${\displaystyle \Sigma _{1}^{0,Y}}$${\displaystyle \Delta _{0}^{0,Y}}$

Арифметическая сводимость — промежуточное понятие между сводимостью по Тьюрингу и гиперарифметической сводимостью .

Множество является арифметическим (также арифметическим и арифметически определимым ), если оно определяется некоторой формулой на языке арифметики Пеано. Эквивалентно X является арифметическим, если X является или для некоторого натурального числа n . Множество X является арифметическим во множестве Y , обозначаемом , если X определимо как некоторая формула на языке арифметики Пеано, расширенная предикатом для принадлежности Y . Эквивалентно, X является арифметическим в Y , если X является в или для некоторого натурального числа n . Синонимом для является: X арифметически сводимо к Y .${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$ ${\displaystyle X\leq _{A}Y}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Pi _{n}^{0,Y}}$${\displaystyle X\leq _{A}Y}$

Отношение рефлексивно и транзитивно , и, таким образом , отношение определяется правилом${\displaystyle X\leq _{A}Y}$${\displaystyle \equiv _{A}}$

${\displaystyle X\equiv _{A}Y\iff X\leq _{A}Y\land Y\leq _{A}X}$

является отношением эквивалентности . Классы эквивалентности этого отношения называются арифметическими степенями ; они частично упорядочены по .${\displaystyle \leq _{A}}$

Пространство Кантора , обозначаемое , представляет собой множество всех бесконечных последовательностей нулей и единиц; пространство Бэра , обозначаемое или , представляет собой множество всех бесконечных последовательностей натуральных чисел. Обратите внимание, что элементы пространства Кантора можно отождествить с множествами натуральных чисел, а элементы пространства Бэра — с функциями от натуральных чисел до натуральных чисел.${\displaystyle 2^{\omega }}$${\displaystyle \omega ^{\omega }}$${\displaystyle {\mathcal {N}}}$

Обычная аксиоматизация арифметики второго порядка использует язык, основанный на множествах, в котором квантификаторы множеств естественным образом можно рассматривать как квантифицирующие по пространству Кантора. Подмножеству пространства Кантора назначается классификация , если оно определяется формулой . Множеству назначается классификация , если оно определяется формулой . Если множество является и тем , и другим, то ему дается дополнительная классификация . Например, пусть будет множеством всех бесконечных двоичных строк, которые не являются всеми 0 (или, что эквивалентно, множеством всех непустых множеств натуральных чисел). Как мы видим, это определяется формулой и, следовательно, является множеством.${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle O\subseteq 2^{\omega }}$${\displaystyle O=\{X\in 2^{\omega }|\exists n(X(n)=1)\}}$${\displaystyle O}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$

Обратите внимание, что хотя элементы пространства Кантора (рассматриваемые как множества натуральных чисел) и подмножества пространства Кантора классифицируются в арифметических иерархиях, это не одна и та же иерархия. На самом деле, связь между двумя иерархиями интересна и нетривиальна. Например, элементы пространства Кантора (в общем случае) не совпадают с элементами пространства Кантора, так что это подмножество пространства Кантора. Однако многие интересные результаты связывают эти две иерархии.${\displaystyle \Pi _{n}^{0}}$${\displaystyle X}$${\displaystyle \{X\}}$${\displaystyle \Pi _{n}^{0}}$

Существует два способа классификации подмножества пространства Бэра в арифметической иерархии.

• Подмножество пространства Бэра имеет соответствующее подмножество пространства Кантора под отображением, которое переводит каждую функцию из в в характеристическую функцию ее графика. Подмножеству пространства Бэра присваивается классификация , , или тогда и только тогда, когда соответствующее подмножество пространства Кантора имеет ту же классификацию.${\displaystyle \omega }$${\displaystyle \omega }$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$
• Эквивалентное определение арифметической иерархии на пространстве Бэра дается путем определения арифметической иерархии формул с использованием функциональной версии арифметики второго порядка; затем арифметическая иерархия на подмножествах пространства Кантора может быть определена из иерархии на пространстве Бэра. Это альтернативное определение дает точно такие же классификации, как и первое определение.

Параллельное определение используется для определения арифметической иерархии на конечных декартовых степенях пространства Бэра или пространства Кантора, используя формулы с несколькими свободными переменными. Арифметическая иерархия может быть определена на любом эффективном польском пространстве ; определение особенно просто для пространства Кантора и пространства Бэра, поскольку они соответствуют языку обычной арифметики второго порядка.

Обратите внимание, что мы также можем определить арифметическую иерархию подмножеств пространств Кантора и Бэра относительно некоторого множества натуральных чисел. Фактически, жирный шрифт — это просто объединение для всех множеств натуральных чисел Y . Обратите внимание, что жирная иерархия — это просто стандартная иерархия множеств Бореля .${\displaystyle \mathbf {\Sigma } _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$

Можно определить арифметическую иерархию формул, используя язык, расширенный символом функции для каждой примитивной рекурсивной функции . Эта вариация немного меняет классификацию , поскольку использование примитивных рекурсивных функций в арифметике Пеано первого порядка требует, как правило, неограниченного квантификатора существования, и, таким образом, некоторые множества, которые находятся в по этому определению, строго находятся в по определению, данному в начале этой статьи. Класс и, таким образом, все более высокие классы в иерархии остаются неизменными.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \Sigma _{0}^{0}}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$

Более семантическая вариация иерархии может быть определена для всех конечных отношений на натуральных числах; используется следующее определение. Каждое вычислимое отношение определяется как . Классификации и определяются индуктивно с помощью следующих правил.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

• Если отношение равно , то отношение определяется как${\displaystyle R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle S(n_{1},\ldots ,n_{l})=\forall m_{1}\cdots \forall m_{k}R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})}$${\displaystyle \Pi _{n+1}^{0}}$
• Если отношение равно , то отношение определяется как${\displaystyle R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle S(n_{1},\ldots ,n_{l})=\exists m_{1}\cdots \exists m_{k}R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})}$${\displaystyle \Sigma _{n+1}^{0}}$

Эта вариация немного меняет классификацию некоторых множеств. В частности, , как класс множеств (определяемый отношениями в классе), идентичен тому, как последний был определен ранее. Его можно расширить, чтобы охватить финитные отношения на натуральных числах, пространстве Бэра и пространстве Кантора.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \Delta _{1}^{0}}$

Для арифметической иерархии множеств натуральных чисел и арифметической иерархии подмножеств пространства Кантора или Бэра справедливы следующие свойства.

• Коллекции и замкнуты относительно конечных объединений и конечных пересечений своих соответствующих элементов.${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$
• Множество есть тогда и только тогда, когда его дополнение есть . Множество есть тогда и только тогда, когда множество есть и , в этом случае его дополнение также будет .${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$
• Включения и справедливы для всех . Таким образом, иерархия не разрушается. Это прямое следствие теоремы Поста .${\displaystyle \Pi _{n}^{0}\subsetneq \Pi _{n+1}^{0}}$${\displaystyle \Sigma _{n}^{0}\subsetneq \Sigma _{n+1}^{0}}$${\displaystyle n}$
• Включения , и справедливы для .${\displaystyle \Delta _{n}^{0}\subsetneq \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}\subsetneq \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}\cup \Pi _{n}^{0}\subsetneq \Delta _{n+1}^{0}}$${\displaystyle n\geq 1}$

• Например, для универсальной машины Тьюринга T множество пар ( n , m ) таких, что T останавливается на n , но не на m , входит в (будучи вычислимым с помощью оракула для проблемы остановки), но не входит в .${\displaystyle \Delta _{2}^{0}}$${\displaystyle \Sigma _{1}^{0}\cup \Pi _{1}^{0}}$
• ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}=\Sigma _{0}^{0}\cup \Pi _{0}^{0}\subseteq \Delta _{1}^{0}}$. Включение является строгим согласно определению, данному в этой статье, но тождество с имеет место при одном из вариантов определения, данного выше.${\displaystyle \Delta _{1}^{0}}$

Если S — вычислимое по Тьюрингу множество , то и S , и его дополнение рекурсивно перечислимы (если T — машина Тьюринга, возвращающая 1 для входных данных в S и 0 в противном случае, мы можем построить машину Тьюринга, останавливающуюся только на первом, и другую, останавливающуюся только на втором).

По теореме Поста , и S , и его дополнение находятся в . Это означает, что S находится как в , так и в , и, следовательно, он находится в .${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$${\displaystyle \Pi _{1}^{0}}$${\displaystyle \Delta _{1}^{0}}$

Аналогично, для каждого множества S в , как S , так и его дополнение находятся в и, следовательно, (по теореме Поста ) рекурсивно перечислимы некоторыми машинами Тьюринга T ₁ и T ₂ , соответственно. Для каждого числа n ровно одна из них останавливается. Поэтому мы можем построить машину Тьюринга T , которая попеременно работает между T ₁ и T ₂ , останавливаясь и возвращая 1, когда останавливается первая, или останавливаясь и возвращая 0, когда останавливается последняя. Таким образом, T останавливается на каждом n и возвращает, находится ли она в S ; поэтому S вычислимо.${\displaystyle \Delta _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$

Вычислимые по Тьюрингу множества натуральных чисел — это в точности множества на уровне арифметической иерархии. Рекурсивно перечислимые множества — это в точности множества на уровне .${\displaystyle \Delta _{1}^{0}}$${\displaystyle \Sigma _{1}^{0}}$

Ни одна машина-оракул не способна решить собственную проблему остановки (применяется вариация доказательства Тьюринга). Проблема остановки для оракула на самом деле находится в .${\displaystyle \Delta _{n}^{0,Y}}$${\displaystyle \Sigma _{n+1}^{0,Y}}$

Теорема Поста устанавливает тесную связь между арифметической иерархией множеств натуральных чисел и степенями Тьюринга . В частности, она устанавливает следующие факты для всех n ≥ 1:

• Множество ( n- й скачок Тьюринга пустого множества) является многоединичным за .${\displaystyle \emptyset ^{(n)}}$${\displaystyle \Sigma _{n}^{0}}$
• В комплект входит несколько предметов по одному .${\displaystyle \mathbb {N} \setminus \emptyset ^{(n)}}$${\displaystyle \Pi _{n}^{0}}$
• Набор является полным по Тьюрингу .${\displaystyle \emptyset ^{(n-1)}}$${\displaystyle \Delta _{n}^{0}}$

Полиномиальная иерархия — это «допустимая ограниченная ресурсами» версия арифметической иерархии, в которой на участвующие числа накладываются полиномиальные ограничения длины (или, что эквивалентно, полиномиальные ограничения времени накладываются на участвующие машины Тьюринга). Она дает более тонкую классификацию некоторых множеств натуральных чисел, которые находятся на уровне арифметической иерархии.${\displaystyle \Delta _{1}^{0}}$

• Аналитическая иерархия
• Иерархия Леви
• Иерархия (математика)
• Логика интерпретируемости
• Полиномиальная иерархия