индекс Жаккара

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2011) (Learn how and when to remove this message)

Индекс Жаккара — это статистика, используемая для оценки сходства и разнообразия выборочных наборов. В общем случае он определяется как отношение двух размеров (площадей или объемов), размера пересечения, деленного на размер объединения, также называемого пересечением по объединению ( IoU ).

Он был разработан Гроувом Карлом Гилбертом в 1884 году как его отношение проверки (v) ^[1] и теперь часто называется критическим индексом успеха в метеорологии. ^[2] Позднее он был разработан независимо Полем Жаккаром , первоначально дав ему французское название factor de communauté (коэффициент общности), ^{[3] [4]} и независимо сформулирован заново Т. Танимото. ^[5] Таким образом, в некоторых областях его также называют индексом Танимото или коэффициентом Танимото .

Индекс Жаккара измеряет сходство между конечными выборками и определяется как размер пересечения, деленный на размер объединения выборок:

${\displaystyle J(A,B)={\frac {|A\cap B|}{|A\cup B|}}={\frac {|A\cap B|}{|A|+|B|-|A\cap B|}}.}$

Обратите внимание, что по замыслу, если пересечение A B пусто, то J ( A ,  B ) = 0. Индекс Жаккара широко используется в информатике, экологии, геномике и других науках, где используются бинарные или бинаризированные данные . Для проверки гипотез с помощью индекса Жаккара доступны как точные решения, так и методы приближения. ^[6]${\displaystyle 0\leq J(A,B)\leq 1.}$

Подобие Жаккара также применимо к сумкам, т. е. мультимножествам . Это имеет похожую формулу, ^[7], но используемые символы представляют пересечение сумок и сумму сумок (не объединение). Максимальное значение равно 1/2.

${\displaystyle J(A,B)={\frac {|A\cap B|}{|A\uplus B|}}={\frac {|A\cap B|}{|A|+|B|}}.}$

Расстояние Жаккара , которое измеряет несходство между выборочными наборами, является дополнительным к индексу Жаккара и получается путем вычитания индекса Жаккара из 1 или, что эквивалентно, путем деления разницы размеров объединения и пересечения двух наборов на размер объединения:

${\displaystyle d_{J}(A,B)=1-J(A,B)={\frac {|A\cup B|-|A\cap B|}{|A\cup B|}}.}$

Альтернативная интерпретация расстояния Жаккара — это отношение размера симметричной разности к объединению. Расстояние Жаккара обычно используется для вычисления матрицы n × n для кластеризации и многомерного масштабирования n выборочных наборов.${\displaystyle A\mathbin {\triangle } B=(A\cup B)-(A\cap B)}$

Это расстояние является метрикой на совокупности всех конечных множеств. ^{[8] [9] [10]}

Существует также версия расстояния Жаккара для мер , включая вероятностные меры . Если есть мера на измеримом пространстве , то мы определяем индекс Жаккара как${\displaystyle \mu }$ ${\displaystyle X}$

${\displaystyle J_{\mu }(A,B)={\frac {\mu (A\cap B)}{\mu (A\cup B)}},}$

и расстояние Жаккара по

${\displaystyle d_{\mu }(A,B)=1-J_{\mu }(A,B)={\frac {\mu (A\mathbin {\triangle } B)}{\mu (A\cup B)}}.}$

Необходимо соблюдать осторожность, если или , поскольку в этих случаях эти формулы определены нечетко.${\displaystyle \mu (A\cup B)=0}$${\displaystyle \infty }$

Схема хеширования MinHash с минимальными независимыми перестановками, чувствительная к локальности , может использоваться для эффективного вычисления точной оценки индекса сходства Жаккара пар наборов, где каждый набор представлен сигнатурой постоянного размера, полученной из минимальных значений хеш-функции .

При наличии двух объектов, A и B , каждый из которых имеет n двоичных атрибутов, индекс Жаккара является полезной мерой перекрытия, которое A и B разделяют со своими атрибутами. Каждый атрибут A и B может быть равен 0 или 1. Общее количество каждой комбинации атрибутов для A и B указывается следующим образом:

${\displaystyle M_{11}}$представляет собой общее количество атрибутов, где A и B оба имеют значение 1.

${\displaystyle M_{01}}$представляет собой общее количество атрибутов, где атрибут A равен 0, а атрибут B равен 1.

${\displaystyle M_{10}}$представляет собой общее количество атрибутов, где атрибут A равен 1, а атрибут B равен 0.

${\displaystyle M_{00}}$представляет собой общее количество атрибутов, где A и B оба имеют значение 0.

А Б	0	1
0	${\displaystyle M_{00}}$	${\displaystyle M_{10}}$
1	${\displaystyle M_{01}}$	${\displaystyle M_{11}}$

Каждый атрибут должен попадать в одну из этих четырех категорий, что означает, что

${\displaystyle M_{11}+M_{01}+M_{10}+M_{00}=n.}$

Индекс сходства Жаккара, J , определяется как

${\displaystyle J={M_{11} \over M_{01}+M_{10}+M_{11}}.}$

Расстояние Жаккара, d _J , определяется как

${\displaystyle d_{J}={M_{01}+M_{10} \over M_{01}+M_{10}+M_{11}}=1-J.}$

Статистический вывод может быть сделан на основе индекса сходства Жаккара и, следовательно, связанных метрик. ^[6] При наличии двух выборочных наборов A и B с n атрибутами можно провести статистический тест, чтобы увидеть, является ли перекрытие статистически значимым . Точное решение доступно, хотя вычисление может быть дорогостоящим по мере увеличения n . ^[6] Методы оценки доступны либо путем аппроксимации полиномиального распределения , либо путем бутстреппинга. ^[6]

При использовании для бинарных атрибутов индекс Жаккара очень похож на простой коэффициент соответствия . Главное отличие состоит в том, что SMC имеет термин в числителе и знаменателе, тогда как индекс Жаккара не имеет. Таким образом, SMC учитывает как взаимное присутствие (когда атрибут присутствует в обоих наборах), так и взаимное отсутствие (когда атрибут отсутствует в обоих наборах) как совпадения и сравнивает их с общим числом атрибутов во вселенной, тогда как индекс Жаккара учитывает только взаимное присутствие как совпадения и сравнивает его с числом атрибутов, которые были выбраны хотя бы одним из двух наборов.${\displaystyle M_{00}}$

Например, в анализе рыночной корзины корзина двух потребителей, которых мы хотим сравнить, может содержать лишь малую часть всех доступных в магазине продуктов, поэтому SMC обычно возвращает очень высокие значения сходства, даже если корзины имеют очень мало сходства, что делает индекс Жаккара более подходящей мерой сходства в этом контексте. Например, рассмотрим супермаркет с 1000 продуктами и двумя покупателями. Корзина первого покупателя содержит соль и перец, а корзина второго — соль и сахар. В этом сценарии сходство между двумя корзинами, измеренное индексом Жаккара, составит 1/3, но сходство становится 0,998 при использовании SMC.

В других контекстах, где 0 и 1 несут эквивалентную информацию (симметрию), SMC является лучшей мерой сходства. Например, векторы демографических переменных, хранящихся в фиктивных переменных , таких как пол, лучше сравнивать с SMC, чем с индексом Жаккара, поскольку влияние пола на сходство должно быть равным, независимо от того, определен ли мужской пол как 0, а женский как 1 или наоборот. Однако, когда у нас есть симметричные фиктивные переменные, можно воспроизвести поведение SMC, разделив фиктивные переменные на два бинарных атрибута (в данном случае мужской и женский), тем самым преобразуя их в асимметричные атрибуты, что позволяет использовать индекс Жаккара без внесения каких-либо смещений. Однако SMC остается более вычислительно эффективным в случае симметричных фиктивных переменных, поскольку он не требует добавления дополнительных измерений.

Если и — два вектора, все из которых действительны , то их индекс сходства Жаккара (также известный как индекс сходства Ружички) определяется как${\displaystyle \mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})}$${\displaystyle \mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})}$${\displaystyle x_{i},y_{i}\geq 0}$

${\displaystyle J_{\mathcal {W}}(\mathbf {x} ,\mathbf {y} )={\frac {\sum _{i}\min(x_{i},y_{i})}{\sum _{i}\max(x_{i},y_{i})}},}$

и расстояние Жаккара (также известное как расстояние Зёргеля)

${\displaystyle d_{J{\mathcal {W}}}(\mathbf {x} ,\mathbf {y} )=1-J_{\mathcal {W}}(\mathbf {x} ,\mathbf {y} ).}$

С еще большей общностью, если и — две неотрицательные измеримые функции на измеримом пространстве с мерой , то мы можем определить${\displaystyle f}$${\displaystyle g}$${\displaystyle X}$${\displaystyle \mu }$

${\displaystyle J_{\mathcal {W}}(f,g)={\frac {\int \min(f,g)d\mu }{\int \max(f,g)d\mu }},}$

где и — точечные операторы. Тогда расстояние Жаккара равно${\displaystyle \max }$${\displaystyle \min }$

${\displaystyle d_{J{\mathcal {W}}}(f,g)=1-J_{\mathcal {W}}(f,g).}$

Тогда, например, для двух измеримых множеств имеем, где и — характеристические функции соответствующего множества.${\displaystyle A,B\subseteq X}$${\displaystyle J_{\mu }(A,B)=J(\chi _{A},\chi _{B}),}$${\displaystyle \chi _{A}}$${\displaystyle \chi _{B}}$

Взвешенное сходство Жаккара, описанное выше, обобщает индекс Жаккара на положительные векторы, где набор соответствует двоичному вектору, заданному индикаторной функцией , т.е. . Однако это не обобщает индекс Жаккара на распределения вероятностей, где набор соответствует равномерному распределению вероятностей, т.е.${\displaystyle x_{i}\in \{0,1\}}$

${\displaystyle x_{i}={\begin{cases}{\frac {1}{|X|}}&i\in X\\0&{\text{otherwise}}\end{cases}}}$

Он всегда меньше, если множества различаются по размеру. Если , и тогда${\displaystyle |X|>|Y|}$${\displaystyle x_{i}=\mathbf {1} _{X}(i)/|X|,y_{i}=\mathbf {1} _{Y}(i)/|Y|}$

${\displaystyle J_{\mathcal {W}}(x,y)={\frac {|X\cap Y|}{|X\setminus Y|+|X|}}<J(X,Y).}$

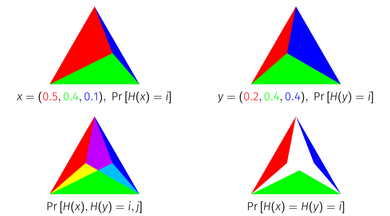
Вместо этого обобщение, которое является непрерывным между распределениями вероятностей и соответствующими им опорными множествами,

${\displaystyle J_{\mathcal {P}}(x,y)=\sum _{x_{i}\neq 0,y_{i}\neq 0}{\frac {1}{\sum _{j}\max \left({\frac {x_{j}}{x_{i}}},{\frac {y_{j}}{y_{i}}}\right)}}}$

который называется «вероятностным» Жаккаром. ^[11] Он имеет следующие границы по сравнению с взвешенным Жаккаром на векторах вероятностей.

${\displaystyle J_{\mathcal {W}}(x,y)\leq J_{\mathcal {P}}(x,y)\leq {\frac {2J_{\mathcal {W}}(x,y)}{1+J_{\mathcal {W}}(x,y)}}}$

Здесь верхняя граница — это (взвешенный) коэффициент Сёренсена–Дайса . Соответствующее расстояние , является метрикой над распределениями вероятностей и псевдометрикой над неотрицательными векторами.${\displaystyle 1-J_{\mathcal {P}}(x,y)}$

Индекс вероятности Жаккара имеет геометрическую интерпретацию как площадь пересечения симплексов . Каждая точка на единичном симплексе соответствует распределению вероятностей по элементам, поскольку единичный симплекс — это набор точек в измерениях, сумма которых равна 1. Чтобы геометрически вывести индекс вероятности Жаккара, представьте распределение вероятностей как единичный симплекс, разделенный на подсимплексы в соответствии с массой каждого элемента. Если наложить два распределения, представленные таким образом, друг на друга и пересечь симплексы, соответствующие каждому элементу, то оставшаяся площадь будет равна индексу вероятности Жаккара распределений.${\displaystyle k}$${\displaystyle k+1}$${\displaystyle k}$${\displaystyle k+1}$

Рассмотрим задачу построения случайных величин таким образом, чтобы они сталкивались друг с другом как можно чаще. То есть, если и , мы хотели бы построить и , чтобы максимизировать . Если мы рассмотрим только два распределения изолированно, то самое большое, чего мы можем достичь, определяется выражением , где — расстояние общей вариации . Однако предположим, что мы не просто озабочены максимизацией этой конкретной пары, предположим, что мы хотели бы максимизировать вероятность столкновения любой произвольной пары. Можно построить бесконечное количество случайных величин, по одной для каждого распределения , и стремиться максимизировать для всех пар . В довольно строгом смысле, описанном ниже, индекс вероятности Жаккара является оптимальным способом выравнивания этих случайных величин.${\displaystyle X\sim x}$${\displaystyle Y\sim y}$${\displaystyle X}$${\displaystyle Y}$${\displaystyle \Pr[X=Y]}$${\displaystyle x,y}$${\displaystyle \Pr[X=Y]}$${\displaystyle 1-{\text{TV}}(x,y)}$${\displaystyle {\text{TV}}}$${\displaystyle x}$${\displaystyle \Pr[X=Y]}$${\displaystyle x,y}$

Для любого метода выборки и дискретных распределений , если тогда для некоторых где и , либо , либо . ^[11]${\displaystyle G}$${\displaystyle x,y}$${\displaystyle \Pr[G(x)=G(y)]>J_{\mathcal {P}}(x,y)}$${\displaystyle z}$${\displaystyle J_{\mathcal {P}}(x,z)>J_{\mathcal {P}}(x,y)}$${\displaystyle J_{\mathcal {P}}(y,z)>J_{\mathcal {P}}(x,y)}$${\displaystyle \Pr[G(x)=G(z)]<J_{\mathcal {P}}(x,z)}$${\displaystyle \Pr[G(y)=G(z)]<J_{\mathcal {P}}(y,z)}$

То есть, ни один метод выборки не может достичь большего количества коллизий, чем на одной паре, не достигая меньшего количества коллизий, чем на другой паре, где уменьшенная пара более похожа по сравнению с увеличенной парой. Эта теорема верна для индекса Жаккара множеств (если интерпретировать как равномерные распределения) и вероятности Жаккара, но не для взвешенного Жаккара. (Теорема использует слово «метод выборки» для описания совместного распределения по всем распределениям в пространстве, потому что она вытекает из использования алгоритмов взвешенного минхеширования , которые достигают этого как своей вероятности коллизии.)${\displaystyle J_{\mathcal {P}}}$${\displaystyle J_{\mathcal {P}}}$${\displaystyle J_{\mathcal {P}}}$

Эта теорема имеет наглядное доказательство на основе трехэлементных распределений с использованием симплексного представления.

Различные формы функций, описанные как сходство Танимото и расстояние Танимото, встречаются в литературе и в Интернете. Большинство из них являются синонимами сходства Жаккара и расстояния Жаккара, но некоторые математически различны. Многие источники ^[12] ссылаются на технический отчет IBM ^[5] как на основополагающую ссылку.

В "Компьютерной программе классификации растений", опубликованной в октябре 1960 года, ^[13] дается метод классификации, основанный на отношении сходства и выведенной функции расстояния. Кажется, что это наиболее авторитетный источник для значения терминов "сходство Танимото" и "расстояние Танимото". Отношение сходства эквивалентно сходству Жаккара, но функция расстояния не совпадает с расстоянием Жаккара.

В этой статье "коэффициент подобия" дается для битовых карт , где каждый бит массива фиксированного размера представляет наличие или отсутствие характеристики в моделируемой установке. Определение коэффициента - это количество общих битов, деленное на количество установленных битов ( т.е. ненулевых) в каждом образце.

В математических терминах, если образцы X и Y являются битовыми изображениями, i -й бит X , а побитовые и , или операторы соответственно, то коэффициент подобия равен${\displaystyle X_{i}}$${\displaystyle \land ,\lor }$ ${\displaystyle T_{s}}$

${\displaystyle T_{s}(X,Y)={\frac {\sum _{i}(X_{i}\land Y_{i})}{\sum _{i}(X_{i}\lor Y_{i})}}}$

Если вместо этого каждый образец моделируется как набор атрибутов, это значение равно индексу Жаккара двух наборов. Жаккар не цитируется в статье, и, похоже, авторы не знали об этом. ^{[ необходима цитата ]}

Танимото продолжает определять «расстояние» на основе этого отношения, определенного для растровых изображений с ненулевым сходством:

${\displaystyle T_{d}(X,Y)=-\log _{2}(T_{s}(X,Y))}$

Этот коэффициент намеренно не является метрикой расстояния. Он выбран, чтобы допустить возможность того, что два образца, которые сильно отличаются друг от друга, оба будут похожи на третий. Легко построить пример, который опровергает свойство неравенства треугольника .

Расстояние Танимото часто ошибочно называют синонимом расстояния Жаккара . Эта функция является надлежащей метрикой расстояния. «Расстояние Танимото» часто называют надлежащей метрикой расстояния, вероятно, из-за его путаницы с расстоянием Жаккара. ^{[ требуется пояснение ] [ требуется цитата ]}${\displaystyle 1-T_{s}}$

Если сходство Жаккара или Танимото выражается через битовый вектор, то его можно записать как

${\displaystyle f(A,B)={\frac {A\cdot B}{\|A\|^{2}+\|B\|^{2}-A\cdot B}}}$

где тот же расчет выражается в терминах векторного скалярного произведения и величины. Это представление основано на том факте, что для битового вектора (где значение каждого измерения равно 0 или 1) тогда

${\displaystyle A\cdot B=\sum _{i}A_{i}B_{i}=\sum _{i}(A_{i}\land B_{i})}$

и

${\displaystyle \|A\|^{2}=\sum _{i}A_{i}^{2}=\sum _{i}A_{i}.}$

Это потенциально запутанное представление, поскольку функция, выраженная по векторам, является более общей, если только ее область определения явно не ограничена. Свойства не обязательно распространяются на . В частности, функция разности не сохраняет неравенство треугольника и, следовательно, не является надлежащей метрикой расстояния, тогда как является.${\displaystyle T_{s}}$${\displaystyle f}$${\displaystyle 1-f}$${\displaystyle 1-T_{s}}$

Существует реальная опасность того, что сочетание определения «расстояния Танимото» с помощью этой формулы и утверждения «расстояние Танимото является надлежащей метрикой расстояния» приведет к ложному выводу о том, что функция на самом деле является метрикой расстояния по векторам или мультимножествам в целом, тогда как ее использование в алгоритмах поиска по сходству или кластеризации может не дать правильных результатов.${\displaystyle 1-f}$

Липкус ^[9] использует определение сходства Танимото, которое эквивалентно , и ссылается на расстояние Танимото как на функцию . Однако в статье ясно указано, что контекст ограничен использованием (положительного) вектора веса, так что для любого рассматриваемого вектора A при этих обстоятельствах функция является надлежащей метрикой расстояния, и поэтому набор векторов, управляемых таким вектором веса, образует метрическое пространство под этой функцией.${\displaystyle f}$${\displaystyle 1-f}$${\displaystyle W}$${\displaystyle A_{i}\in \{0,W_{i}\}.}$

В матрицах путаницы, используемых для бинарной классификации , индекс Жаккара можно представить в виде следующей формулы:

${\displaystyle {\text{Jaccard index}}={\frac {TP}{TP+FP+FN}}}$

где TP — истинно положительные результаты, FP — ложноположительные результаты, а FN — ложноотрицательные результаты. ^[14]

• Коэффициент перекрытия
• Простой коэффициент соответствия
• Расстояние Хэмминга
• Коэффициент Сёренсена–Дайса , что эквивалентно: и ( : индекс Жаккара, : коэффициент Сёренсена–Дайса)${\displaystyle J=S/(2-S)}$${\displaystyle S=2J/(1+J)}$${\displaystyle J}$${\displaystyle S}$
• индекс Тверски
• Корреляция
• Взаимная информация , нормализованным метрическим вариантом которой является энтропийное расстояние Жаккара.

• Введение в Data Mining, лекции от Тана, Штайнбаха, Кумара
• Kaggle Dstl Спутниковые изображения Определение характеристик - Оценка