Ионизация

Ионизация (или ионизация в частности в Великобритании, Ирландии, Австралии и Новой Зеландии) - это процесс, посредством которого атом или молекула приобретает отрицательный или положительный заряд , приобретая или теряя электроны , часто в сочетании с другими химическими изменениями. Полученный электрически заряженный атом или молекула называется ионом . Ионизация может быть результатом потери электрона после столкновений с субатомными частицами , столкновений с другими атомами, молекулами, электронами, позитронами , [1] протонами , антипротонами [2] и ионами, [3] [4 ] [5] [6] [7] [8] [9] или посредством взаимодействия с электромагнитным излучением . Гетеролитический разрыв связей и реакции гетеролитического замещения могут приводить к образованию ионных пар. Ионизация может происходить посредством радиоактивного распада посредством процесса внутренней конверсии , в котором возбужденное ядро передает свою энергию одному из электронов внутренней оболочки, заставляя его выбрасываться.
Использует
Повседневные примеры ионизации газа происходят в люминесцентной лампе или других электрических разрядных лампах. Она также используется в детекторах излучения, таких как счетчик Гейгера-Мюллера или ионизационная камера . Процесс ионизации широко используется в различном оборудовании в фундаментальной науке (например, масс-спектрометрия ) и в лечении (например, лучевая терапия ). Она также широко используется для очистки воздуха, хотя исследования показали вредные эффекты этого применения. [10] [11]
Производство ионов

Отрицательно заряженные ионы [12] образуются, когда свободный электрон сталкивается с атомом и впоследствии оказывается в ловушке внутри электрического потенциального барьера, высвобождая избыточную энергию. Этот процесс известен как ионизация с захватом электронов .
Положительно заряженные ионы производятся путем передачи некоторого количества энергии связанному электрону при столкновении с заряженными частицами (например, ионами, электронами или позитронами) или с фотонами. Пороговое количество требуемой энергии известно как потенциал ионизации . Изучение таких столкновений имеет фундаментальное значение в отношении проблемы нескольких тел , которая является одной из главных нерешенных проблем в физике. Кинематически полные эксперименты [13] , т. е. эксперименты, в которых определяются полный вектор импульса всех фрагментов столкновения (рассеянный снаряд, отскакивающий ион-мишень и выброшенный электрон), внесли значительный вклад в теоретическое понимание проблемы нескольких тел в последние годы.
Адиабатическая ионизация
Адиабатическая ионизация — это форма ионизации, при которой электрон удаляется из атома или молекулы в ее самом низком энергетическом состоянии или добавляется к ним , образуя ион в его самом низком энергетическом состоянии. [14]
Разряд Таунсенда является хорошим примером создания положительных ионов и свободных электронов из-за удара ионов. Это каскадная реакция с участием электронов в области с достаточно высоким электрическим полем в газообразной среде, которая может быть ионизирована, такой как воздух . После первоначального события ионизации, вызванного, например, ионизирующим излучением, положительный ион дрейфует к катоду , в то время как свободный электрон дрейфует к аноду устройства . Если электрическое поле достаточно сильное, свободный электрон получает достаточную энергию, чтобы освободить еще один электрон, когда он в следующий раз столкнется с другой молекулой. Затем два свободных электрона движутся к аноду и получают достаточную энергию от электрического поля, чтобы вызвать ударную ионизацию, когда происходят следующие столкновения; и так далее. Это фактически цепная реакция генерации электронов, и она зависит от того, получают ли свободные электроны достаточно энергии между столкновениями, чтобы поддерживать лавину. [15]
Эффективность ионизации – это отношение числа образованных ионов к числу использованных электронов или фотонов. [16] [17]
Энергия ионизации атомов

Тенденция энергии ионизации атомов часто используется для демонстрации периодического поведения атомов относительно атомного номера, как это суммировано путем упорядочения атомов в таблице Менделеева . Это ценный инструмент для установления и понимания упорядочения электронов на атомных орбиталях, не вдаваясь в детали волновых функций или процесса ионизации. Пример представлен на рисунке справа. Периодическое резкое уменьшение потенциала ионизации после атомов инертных газов, например, указывает на появление новой оболочки в щелочных металлах . Кроме того, локальные максимумы на графике энергии ионизации, движущиеся слева направо в ряд, указывают на подоболочки s, p, d и f.
Полуклассическое описание ионизации
Классическая физика и модель атома Бора могут качественно объяснить фотоионизацию и ионизацию, опосредованную столкновениями. В этих случаях в процессе ионизации энергия электрона превышает разность энергий потенциального барьера, который он пытается преодолеть. Однако классическое описание не может описать туннельную ионизацию , поскольку этот процесс включает прохождение электрона через классически запрещенный потенциальный барьер.
Квантово-механическое описание ионизации
Взаимодействие атомов и молекул с достаточно сильными лазерными импульсами или с другими заряженными частицами приводит к ионизации одно- или многозарядных ионов. Скорость ионизации, т. е. вероятность ионизации в единицу времени, можно рассчитать с помощью квантовой механики . (Существуют также классические методы, такие как метод Монте-Карло с классическими траекториями (CTMC) [18] [19] , но он не является общепринятым и часто критикуется сообществом.) Существуют два квантово-механических метода: пертурбативные и непертурбативные методы, такие как зависящие от времени связанные каналы или независимые от времени методы тесной связи [20] , где волновая функция разлагается в конечном базисном наборе. Доступны многочисленные варианты, например B-сплайны [21] или пакеты кулоновских волн. [22] [23] Другой непертурбативный метод заключается в полном численном решении соответствующего уравнения Шредингера на решетке. [24]
В общем случае аналитические решения недоступны, а аппроксимации, необходимые для управляемых численных расчетов, не дают достаточно точных результатов. Однако, когда интенсивность лазера достаточно высока, детальную структуру атома или молекулы можно игнорировать, и аналитическое решение для скорости ионизации возможно.
Туннельная ионизация

Туннельная ионизация — это ионизация, вызванная квантовым туннелированием . При классической ионизации электрон должен иметь достаточно энергии, чтобы преодолеть потенциальный барьер, но квантовое туннелирование позволяет электрону просто пройти через потенциальный барьер, а не пройти через него полностью из-за волновой природы электрона. Вероятность туннелирования электрона через барьер падает экспоненциально с шириной потенциального барьера. Поэтому электрон с более высокой энергией может пройти дальше по потенциальному барьеру, оставляя гораздо более тонкий барьер для туннелирования и, таким образом, больше шансов сделать это. На практике туннельная ионизация наблюдается, когда атом или молекула взаимодействует с сильными лазерными импульсами ближнего инфракрасного диапазона. Этот процесс можно понимать как процесс, при котором связанный электрон, поглощая более одного фотона из лазерного поля, ионизируется. Эта картина обычно известна как многофотонная ионизация (МФИ).
Келдыш [25] смоделировал процесс MPI как переход электрона из основного состояния атома в состояния Волкова. [26] В этой модели возмущение основного состояния лазерным полем пренебрегается, а детали атомной структуры при определении вероятности ионизации не учитываются. Основной трудностью модели Келдыша было пренебрежение эффектами кулоновского взаимодействия на конечном состоянии электрона. Как видно из рисунка, кулоновское поле не очень мало по величине по сравнению с потенциалом лазера на больших расстояниях от ядра. Это контрастирует с приближением, сделанным путем пренебрежения потенциалом лазера в областях вблизи ядра. Переломов и др. [27] [28] включили кулоновское взаимодействие на больших межъядерных расстояниях. Их модель (которую мы называем моделью PPT) была выведена для короткодействующего потенциала и включает эффект дальнодействующего кулоновского взаимодействия через поправку первого порядка в квазиклассическом действии. Ларошель и др. [29] сравнили теоретически предсказанные кривые ионов и интенсивности атомов инертных газов, взаимодействующих с лазером Ti:Sapphire, с экспериментальными измерениями. Они показали, что полная скорость ионизации, предсказанная моделью PPT, очень хорошо соответствует экспериментальным значениям выхода ионов для всех инертных газов в промежуточном режиме параметра Келдыша.
Скорость MPI на атоме с потенциалом ионизации в линейно поляризованном лазере с частотой определяется выражением
где
- - параметр Келдыша,
- ,
- пиковое электрическое поле лазера и
- .
Коэффициенты и определяются как
Коэффициент определяется по формуле
где
Квазистатическая туннельная ионизация
Квазистатическое туннелирование (QST) — это ионизация, скорость которой может быть удовлетворительно предсказана моделью ADK [30] , т.е. пределом модели PPT, когда она приближается к нулю. [31] Скорость QST определяется выражением
По сравнению с отсутствием суммирования по n, которое представляет различные пики надпороговой ионизации (ATI), это примечательно.
Приближение сильного поля для скорости ионизации
Расчеты PPT производятся в E -калибре, что означает, что лазерное поле рассматривается как электромагнитные волны. Скорость ионизации также может быть рассчитана в A -калибре, который подчеркивает корпускулярную природу света (поглощение нескольких фотонов во время ионизации). Этот подход был принят моделью Крайнова [32] на основе более ранних работ Фейсала [33] и Рейсса. [34] Результирующая скорость определяется как
где:
- с пондеромоторной энергией,
- минимальное количество фотонов, необходимое для ионизации атома,
- — двойная функция Бесселя,
- с углом между импульсом электрона, p , и электрическим полем лазера, F ,
- FT — трехмерное преобразование Фурье, и
- включает поправку Кулона в модель SFA.
Отлов населения
При расчете скорости MPI атомов рассматриваются только переходы в состояния континуума. Такое приближение приемлемо, пока нет многофотонного резонанса между основным состоянием и некоторыми возбужденными состояниями. Однако в реальной ситуации взаимодействия с импульсными лазерами, во время эволюции интенсивности лазера, из-за разного сдвига Штарка основного и возбужденного состояний существует вероятность того, что некоторое возбужденное состояние войдет в многофотонный резонанс с основным состоянием. В картине одетого атома основное состояние, одетое фотонами, и резонансное состояние претерпевают избегаемое пересечение при резонансной интенсивности . Минимальное расстояние, , при избегаемом пересечении пропорционально обобщенной частоте Раби, связывающей два состояния. Согласно Стори и др. [35], вероятность остаться в основном состоянии, , определяется выражением
где — зависящая от времени разность энергий между двумя одетыми состояниями. При взаимодействии с коротким импульсом, если динамический резонанс достигается в восходящей или нисходящей части импульса, заселенность практически остается в основном состоянии, и эффектом многофотонных резонансов можно пренебречь. Однако, если состояния выходят на резонанс на пике импульса, где , то возбужденное состояние заселяется. После заселения, поскольку потенциал ионизации возбужденного состояния мал, ожидается, что электрон мгновенно ионизуется.
В 1992 году де Бур и Мюллер [36] показали, что атомы Xe, подвергнутые воздействию коротких лазерных импульсов, могут выживать в высоковозбужденных состояниях 4f, 5f и 6f. Считалось, что эти состояния возбуждаются динамическим штарковским сдвигом уровней в многофотонный резонанс с полем во время восходящей части лазерного импульса. Последующая эволюция лазерного импульса не полностью ионизует эти состояния, оставляя после себя некоторые высоковозбужденные атомы. Мы будем называть это явление «захватом популяции».

Мы упоминаем теоретический расчет, что неполная ионизация происходит всякий раз, когда есть параллельное резонансное возбуждение на общий уровень с ионизационными потерями. [37] Мы рассматриваем состояние, такое как 6f Xe, которое состоит из 7 квазивырожденных уровней в диапазоне ширины полосы лазера. Эти уровни вместе с континуумом составляют лямбда-систему. Механизм захвата типа лямбда схематически представлен на рисунке. В восходящей части импульса (a) возбужденное состояние (с двумя вырожденными уровнями 1 и 2) не находится в многофотонном резонансе с основным состоянием. Электрон ионизируется посредством многофотонной связи с континуумом. По мере увеличения интенсивности импульса возбужденное состояние и континуум смещаются по энергии из-за сдвига Штарка. На пике импульса (b) возбужденные состояния входят в многофотонный резонанс с основным состоянием. По мере того, как интенсивность начинает уменьшаться (c), два состояния связываются через континуум, и популяция оказывается захваченной в когерентной суперпозиции двух состояний. При последующем воздействии того же импульса, из-за интерференции в амплитудах перехода лямбда-системы, поле не может полностью ионизировать популяцию, и часть популяции будет захвачена в когерентной суперпозиции квазивырожденных уровней. Согласно этому объяснению, состояния с более высоким угловым моментом – с большим количеством подуровней – будут иметь более высокую вероятность захвата популяции. В целом сила захвата будет определяться силой двухфотонной связи между квазивырожденными уровнями через континуум. В 1996 году, используя очень стабильный лазер и минимизируя маскирующие эффекты расширения фокальной области с увеличением интенсивности, Талебпур и др. [38] наблюдали структуры на кривых однозарядных ионов Xe, Kr и Ar. Эти структуры были приписаны захвату электронов в сильном лазерном поле. Более недвусмысленная демонстрация захвата популяции была сообщена Т. Моришита и К. Д. Лином [39] .
Непоследовательная многократная ионизация
Явление непоследовательной ионизации (NSI) атомов, подвергаемых воздействию интенсивных лазерных полей, было предметом многих теоретических и экспериментальных исследований с 1983 года. Пионерская работа началась с наблюдения структуры «колена» на кривой зависимости сигнала иона Xe 2+ от интенсивности Л'Юйе и др. [40] С экспериментальной точки зрения двойная ионизация NS относится к процессам, которые каким-то образом увеличивают скорость образования двухзарядных ионов в огромный раз при интенсивностях ниже интенсивности насыщения однозарядного иона. Многие, с другой стороны, предпочитают определять NSI как процесс, при котором два электрона ионизируются почти одновременно. Это определение подразумевает, что помимо последовательного канала существует еще один канал , который вносит основной вклад в образование двухзарядных ионов при более низких интенсивностях. Первое наблюдение тройной NSI в аргоне, взаимодействующем с 1 мкм лазером, было сообщено Аугстом и др. [41] Позднее, систематически изучая NSI всех атомов инертных газов, была обнаружена четверная NSI Xe. [42] Самым важным выводом этого исследования было наблюдение следующей связи между скоростью NSI для любого зарядового состояния и скоростью туннельной ионизации (предсказываемой формулой ADK) для предыдущих зарядовых состояний;
где — скорость квазистатического туннелирования в i-е зарядовое состояние, а — некоторые константы, зависящие от длины волны лазера (но не от длительности импульса).
Для объяснения непоследовательной ионизации были предложены две модели: модель встряхивания и модель повторного рассеяния электронов. Модель встряхивания (SO), впервые предложенная Фитингхоффом и др. [43] , заимствована из области ионизации атомов рентгеновскими лучами и электронными снарядами, где процесс SO является одним из основных механизмов, ответственных за множественную ионизацию атомов. Модель SO описывает процесс NSI как механизм, в котором один электрон ионизируется лазерным полем, и уход этого электрона происходит настолько быстро, что оставшиеся электроны не успевают приспособиться к новым энергетическим состояниям. Поэтому существует определенная вероятность того, что после ионизации первого электрона второй электрон возбуждается до состояний с более высокой энергией (встряхивание) или даже ионизуется (встряхивание). Следует отметить, что до сих пор не было количественного расчета на основе модели SO, и модель по-прежнему является качественной.
Модель перерассеяния электронов была независимо разработана Кучиевым, [44] Шефером и др. , [45] Коркумом, [46] Беккером и Фейсалом [47] и Фейсалом и Беккером. [48] Основные особенности модели можно легко понять из версии Коркума. Модель Коркума описывает ионизацию NS как процесс, при котором электрон туннельно ионизируется. Затем электрон взаимодействует с лазерным полем, где он ускоряется от ядерного ядра. Если электрон был ионизирован в соответствующей фазе поля, он пройдет мимо положения оставшегося иона на полцикла позже, где он может освободить дополнительный электрон электронным ударом. Только половину времени электрон освобождается с соответствующей фазой, а другую половину он никогда не возвращается в ядерное ядро. Максимальная кинетическая энергия, которую может иметь возвращающийся электрон, в 3,17 раза больше пондеромоторного потенциала ( ) лазера. Модель Коркума устанавливает предельную величину минимальной интенсивности ( λ пропорциональна интенсивности), при которой может произойти ионизация из-за повторного рассеяния.
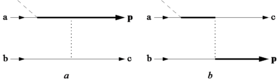
Модель повторного рассеяния в версии Кучиева (модель Кучиева) является квантово-механической. Основная идея модели проиллюстрирована диаграммами Фейнмана на рисунке a. Сначала оба электрона находятся в основном состоянии атома. Линии, обозначенные a и b, описывают соответствующие атомные состояния. Затем электрон a ионизируется. Начало процесса ионизации показано пересечением с наклонной пунктирной линией. где происходит MPI. Распространение ионизированного электрона в лазерном поле, во время которого он поглощает другие фотоны (ATI), показано сплошной толстой линией. Столкновение этого электрона с родительским атомным ионом показано вертикальной пунктирной линией, представляющей кулоновское взаимодействие между электронами. Состояние, обозначенное c, описывает возбуждение иона до дискретного или непрерывного состояния. Рисунок b описывает процесс обмена. Модель Кучиева, в отличие от модели Коркума, не предсказывает никакой пороговой интенсивности для возникновения ионизации NS.
Кучиев не учитывал кулоновские эффекты в динамике ионизированного электрона. Это привело к занижению двойной скорости ионизации в огромный раз. Очевидно, что в подходе Беккера и Фейсала (который по духу эквивалентен модели Кучиева) этот недостаток отсутствует. Фактически, их модель более точна и не страдает от большого количества приближений, сделанных Кучиевым. Результаты их расчетов прекрасно согласуются с экспериментальными результатами Уокера и др. [49]. Беккер и Фейсал [50] смогли подогнать экспериментальные результаты по множественному НСИ атомов инертных газов, используя свою модель. В результате, электронное повторное рассеяние можно принять в качестве основного механизма возникновения процесса НСИ.
Многофотонная ионизация внутренних валентных электронов и фрагментация многоатомных молекул
Ионизация внутренних валентных электронов ответственна за фрагментацию многоатомных молекул в сильных лазерных полях. Согласно качественной модели [51] [52], диссоциация молекул происходит по трехступенчатому механизму:
- МПИ электронов с внутренних орбиталей молекулы, в результате чего молекулярный ион оказывается на вращательно-колебательных уровнях возбужденного электронного состояния;
- Быстрый безызлучательный переход на высоколежащие вращательно-колебательные уровни низшего электронного состояния; и
- Последующая диссоциация иона на различные фрагменты через различные каналы фрагментации.
Молекулярная фрагментация, вызванная коротким импульсом, может использоваться в качестве источника ионов для высокопроизводительной масс-спектроскопии. Селективность, обеспечиваемая источником на основе короткого импульса, превосходит ожидаемую при использовании обычных источников на основе электронной ионизации, в частности, когда требуется идентификация оптических изомеров. [53] [54]
Рамка Крамерса–Хеннебергера
Система Крамерса–Хеннебергера — это неинерциальная система, движущаяся со свободным электроном под воздействием гармонического лазерного импульса, полученная путем применения трансляции к лабораторной системе, равной колебательному движению классического электрона в лабораторной системе. Другими словами, в системе Крамерса–Хеннебергера классический электрон находится в состоянии покоя. [55] Начиная с лабораторной системы (калибровка скорости), мы можем описать электрон с помощью гамильтониана:
В дипольном приближении колебательное движение классического электрона в лабораторной системе отсчета для произвольного поля можно получить из векторного потенциала электромагнитного поля:
где для монохроматической плоской волны.
Применяя преобразование к лабораторной системе отсчета, равное движению колчана, мы переходим к «колеблющейся» или системе «Крамерса–Хеннебергера», в которой классический электрон находится в состоянии покоя. Преобразованием фазового фактора для удобства мы получаем «пространственно-транслированный» гамильтониан, который унитарно эквивалентен гамильтониану лабораторной системы отсчета, который содержит исходный потенциал, центрированный на колеблющейся точке :
Полезность системы отсчета КГ заключается в том, что в этой системе взаимодействие лазера с атомом можно свести к форме осциллирующей потенциальной энергии, где естественными параметрами, описывающими динамику электронов, являются и (иногда называемая «амплитудой отклонения», полученной из ).
Отсюда можно применить теорию Флоке для вычисления квазистационарных решений TDSE. В высокочастотной теории Флоке низший порядок в системе сводится к так называемому «структурному уравнению», которое имеет форму типичного уравнения Шредингера для собственных значений энергии, содержащего «одетый потенциал» (среднее значение цикла осциллирующего потенциала). Интерпретация наличия заключается в следующем: в осциллирующей системе отсчета ядро совершает колебательное движение траектории и может рассматриваться как потенциал размазанного ядерного заряда вдоль его траектории.
Таким образом, рамка КГ используется в теоретических исследованиях ионизации в сильном поле и атомной стабилизации (предсказываемое явление, при котором вероятность ионизации атома в высокоинтенсивном высокочастотном поле фактически уменьшается для интенсивностей выше определенного порога) в сочетании с высокочастотной теорией Флоке. [56]
Диссоциация – различие
Вещество может диссоциировать, не обязательно производя ионы. Например, молекулы столового сахара диссоциируют в воде (сахар растворяется), но существуют как нетронутые нейтральные сущности. Другим тонким событием является диссоциация хлорида натрия (поваренной соли) на ионы натрия и хлора. Хотя это может показаться случаем ионизации, на самом деле ионы уже существуют внутри кристаллической решетки. Когда соль диссоциирует, ее составляющие ионы просто окружены молекулами воды, и их эффекты видны (например, раствор становится электролитическим ). Однако никакого переноса или смещения электронов не происходит.
Смотрите также
- Ионизация выше порога
- Химическая ионизация
- Электронная ионизация
- Ионизационная камера – прибор для обнаружения ионизации газа, используемый при измерении ионизирующего излучения.
- Источник ионов
- Фотоионизация
- Термическая ионизация
- Лавина Таунсенда – цепная реакция ионизации, происходящая в газе с приложенным электрическим полем.
Стол
К От | Твердый | Жидкость | Газ | плазма |
|---|---|---|---|---|
| Твердый | Плавление | Сублимация | ||
| Жидкость | Замораживание | Испарение | ||
| Газ | Отложение | Конденсация | Ионизация | |
| плазма | Рекомбинация |
Ссылки
- ^ Machacek, JR; McEachran, RP; Stauffer, AD (2023). «Positron Collisions». Springer Handbook of Atomic, Molecular, and Optical Physics. Springer Handbooks . Springer. doi :10.1007/978-3-030-73893-8_51. ISBN 978-3-030-73892-1.
- ^ Кирхнер, Том; Кнудсен, Хельге (2011). «Текущее состояние ионизации атомов и молекул антипротонным ударом: теоретические и экспериментальные перспективы». Журнал физики B: атомная, молекулярная и оптическая физика . 44 (12): 122001. doi :10.1088/0953-4075/44/12/122001.
- ^ Брандсен, Б.Х. (1970). Теория атомных столкновений . Бенджамин. ISBN 9780805311808.
- ^ Столтерфохт, Н; Дюбуа, РД; Риварола, Р.Д. (1997). Электронная эмиссия при тяжелых ионно-атомных столкновениях . Спрингер-Верлаг. ISBN 978-3-642-08322-8.
- ^ McGuire, JH (1997). Динамика электронной корреляции в атомных столкновениях . Cambridge University Press. ISBN 9780521480208.
- ^ Эйхлер, Дж. (2005). Лекции по ионно-атомным столкновениям: от нерелятивистских к релятивистским скоростям . Elsevier. ISBN 9780444520470.
- ^ Bransden, BH; McDowell, MRC (1992). Обмен зарядами и теория ионно-атомных столкновений . Clarendon Press; Oxford University Press. ISBN 9780198520207.
- ^ Янев, РК; Пресняков, ЛП; Шевелько, ВП (1985). Физика высокозаряженных ионов . Springer. ISBN 978-3-642-69197-3.
- ^ Шульц, Майкл (2019). Столкновения ионов и атомов. Проблема нескольких тел в динамических системах . De Gruyter. doi : 10.1515/9783110580297. ISBN 9783110579420.
{{cite book}}: CS1 maint: date and year (link) - ^ Waring, MS; Siegel, JA (август 2011 г.). «Влияние генератора ионов на качество воздуха в помещении жилого помещения: влияние генератора ионов на воздух в помещении в помещении». Indoor Air . 21 (4): 267–276. doi : 10.1111/j.1600-0668.2010.00696.x . PMID 21118308.
- ^ Университет штата Колорадо. «Исследование раскрывает проблемы безопасности с ионными очистителями воздуха». phys.org . Получено 28.06.2023 .
- ^ Андерсен, Т (2004). «Атомные отрицательные ионы: структура, динамика и столкновения». Physics Reports . 394 (4–5): 157–313. Bibcode : 2004PhR...394..157A. doi : 10.1016/j.physrep.2004.01.001 – через 157-313.
- ^ Шульц, Майкл (2003). «Трехмерная визуализация атомных четырехтельных процессов». Nature . 422 (6927): 48–51. Bibcode :2003Natur.422...48S. doi :10.1038/nature01415. hdl : 11858/00-001M-0000-0011-8F36-A . PMID 12621427. S2CID 4422064.
- ^ IUPAC , Compendium of Chemical Terminology , 2nd ed. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «адиабатическая ионизация». doi :10.1351/goldbook.A00143
- ^ Гленн Ф. Нолл. Обнаружение и измерение радиации, третье издание 2000 г. John Wiley and sons, ISBN 0-471-07338-5
- ^ Тодд, Дж. Ф. Дж. (1991). «Рекомендации по номенклатуре и символике для масс-спектроскопии (включая приложение терминов, используемых в вакуумной технологии) (Рекомендации ИЮПАК 1991 г.)». Pure Appl. Chem . 63 (10): 1541–1566. doi : 10.1351/pac199163101541 .
- ^ IUPAC , Compendium of Chemical Terminology , 2nd ed. (The "Gold Book") (1997). Онлайн-исправленная версия: (2006–) "ionization efficient". doi :10.1351/goldbook.I03196
- ^ Абринес, Р.; Персиваль, И.С. (1966). «Классическая теория переноса заряда и ионизации атомов водорода протонами». Труды Физического общества . 88 (4): 861–872. doi :10.1088/0370-1328/88/4/306.
- ^ Шульц, DR (1989). «Сравнение процессов удаления одного электрона при столкновениях электронов, позитронов, протонов и антипротонов с водородом и гелием». Phys. Rev. A. 41 ( 5): 2330–2334. doi :10.1103/PhysRevA.40.2330.
- ^ Абдурахманов, ИБ; Плауман, К; Кадыров, АС; Брей, И.; Мухамеджанов, АМ (2020). «Подход одноцентровой тесной связи к столкновениям двухцентровой перестройки». Журнал физики B: атомная, молекулярная и оптическая физика . 53 (14): 145201. doi :10.1088/1361-6455/ab894a. OSTI 1733342.
- ^ Мартин, Фернандо (1999). «Ионизация и диссоциация с использованием B-сплайнов: фотоионизация молекулы водорода». Журнал физики B: атомная, молекулярная и оптическая физика . 32 (16): R197–R231. doi :10.1088/0953-4075/32/16/201.
- ^ Барна, ИФ; Грюн, Н.; Шайд, В. (2003). «Исследование связанных каналов с кулоновскими волновыми пакетами для ионизации гелия при столкновениях тяжелых ионов». European Physical Journal D. 25 ( 3): 239–246. Bibcode : 2003EPJD...25..239B. doi : 10.1140/epjd/e2003-00206-6.
- ^ Абдурахманов, ИБ; Кадыров, АС; Брей, И; Барчат, К. (2017). «Подход волнового пакета континуума-дискретизации к однократной ионизации гелия антипротонами и энергичными протонами». Phys. Rev. A. 96 ( 2): 022702. Bibcode : 2017PhRvA..96b2702A. doi : 10.1103/PhysRevA.96.022702. hdl : 10072/409310 .
- ^ Шульц, DR; Крстич, PS (2003). «Ионизация гелия антипротонами: полностью коррелированный, четырехмерный решеточный подход». Physical Review A. 67 ( 2): 022712. Bibcode : 2003PhRvA..67b2712S. doi : 10.1103/PhysRevA.67.022712.
- ^ Келдыш, Л. В. (1965). «Ионизация в поле сильной электромагнитной волны». Советская физ. ЖЭТФ . 20 (5): 1307.
- ^ Волков Д.М. 1934 З. Физ. 94 250
- ^ Переломов, AM; Попов, VS; Терентьев, MV (1966). "Ионизация атомов в переменном электрическом поле". Советская физическая наука. ЖЭТФ . 23 (5): 924. Bibcode :1966JETP...23..924P. Архивировано из оригинала 2021-03-18 . Получено 2013-08-12 .
- ^ Переломов, AM; Попов, VS; Терентьев, MV (1967). "Ионизация атомов в переменном электрическом поле: II". Soviet Phys. JETP . 24 (1): 207. Bibcode :1967JETP...24..207P. Архивировано из оригинала 2021-03-03 . Получено 2013-08-12 .
- ^ Larochelle, S.; Talebpour, A.; Chin, SL (1998). "Coulomb effect in multiphoton ionization of rare-gas atoms" (PDF) . Journal of Physics B: Atomic, Molecular and Optical Physics . 31 (6): 1215. Bibcode :1998JPhB...31.1215L. doi :10.1088/0953-4075/31/6/009. S2CID 250870476. Архивировано из оригинала (PDF) 21 ноября 2014 г.
- ^ Аммосов, М.В.; Делоне, Н.Б.; Крайнов, В.П. (1986). "Туннельная ионизация сложных атомов и атомарных ионов в переменном электромагнитном поле". Советская физическая наука. ЖЭТФ . 64 (6): 1191. Bibcode : 1986JETP...64.1191A. Архивировано из оригинала 2021-03-01 . Получено 2013-08-12 .
- ^ Sharifi, SM; Talebpour, A; Yang, J.; Chin, SL (2010). «Квазистатическое туннелирование и многофотонные процессы при ионизации Ar и Xe с использованием интенсивных фемтосекундных лазерных импульсов». Journal of Physics B: Atomic, Molecular and Optical Physics . 43 (15): 155601. Bibcode : 2010JPhB...43o5601S. doi : 10.1088/0953-4075/43/15/155601. ISSN 0953-4075. S2CID 121014268.
- ^ Крайнов, Владимир П. (1997). "Скорости ионизации и энергетические и угловые распределения при ионизации сложных атомов и атомарных ионов с подавлением барьера". Журнал оптического общества Америки B. 14 ( 2): 425. Bibcode : 1997JOSAB..14..425K. doi : 10.1364/JOSAB.14.000425. ISSN 0740-3224.
- ^ Faisal, FHM (1973). "Множественное поглощение лазерных фотонов атомами". Journal of Physics B: Atomic and Molecular Physics . 6 (4): L89–L92. Bibcode : 1973JPhB....6L..89F. doi : 10.1088/0022-3700/6/4/011. ISSN 0022-3700.
- ^ Рейсс, Ховард (1980). «Влияние интенсивного электромагнитного поля на слабосвязанную систему». Physical Review A. 22 ( 5): 1786–1813. Bibcode : 1980PhRvA..22.1786R. doi : 10.1103/PhysRevA.22.1786. ISSN 0556-2791.
- ^ Стори, Дж.; Дункан, Д.; Галлахер, Т. (1994). «Тест Ландау-Зенера многофотонных резонансов калия с настройкой интенсивности». Physical Review A. 50 ( 2): 1607–1617. Bibcode : 1994PhRvA..50.1607S. doi : 10.1103/PhysRevA.50.1607. ISSN 1050-2947. PMID 9911054.
- ^ Де Бур, М.; Мюллер, Х. (1992). «Наблюдение больших популяций в возбужденных состояниях после короткоимпульсной многофотонной ионизации». Physical Review Letters . 68 (18): 2747–2750. Bibcode :1992PhRvL..68.2747D. doi :10.1103/PhysRevLett.68.2747. PMID 10045482.
- ^ Hioe, FT; Carrol, CE (1988). «Когерентное удержание популяции в квантовых системах N-уровня». Physical Review A. 37 ( 8): 3000–3005. Bibcode : 1988PhRvA..37.3000H. doi : 10.1103/PhysRevA.37.3000. PMID 9900034.
- ^ Talebpour, A.; Chien, CY; Chin, SL (1996). "Захват популяции в инертных газах". Journal of Physics B: Atomic, Molecular and Optical Physics . 29 (23): 5725. Bibcode : 1996JPhB...29.5725T. doi : 10.1088/0953-4075/29/23/015. S2CID 250757252.
- ^ Моришита, Тору; Лин, К. Д. (2013). «Фотоэлектронные спектры и высокие ридберговские состояния лития, генерируемые интенсивными лазерами в режиме ионизации над барьером» (PDF) . Physical Review A . 87 (6): 63405. Bibcode :2013PhRvA..87f3405M. doi :10.1103/PhysRevA.87.063405. hdl : 2097/16373 . ISSN 1050-2947.
- ^ L'Huillier, A.; Lompre, LA; Mainfray, G.; Manus, C. (1983). "Многозарядные ионы, индуцированные многофотонным поглощением в инертных газах при 0,53 мкм". Physical Review A. 27 ( 5): 2503. Bibcode : 1983PhRvA..27.2503L. doi : 10.1103/PhysRevA.27.2503.
- ^ Augst, S.; Talebpour, A.; Chin, SL; Beaudoin, Y.; Chaker, M. (1995). «Непоследовательная тройная ионизация атомов аргона в высокоинтенсивном лазерном поле». Physical Review A. 52 ( 2): R917–R919. Bibcode : 1995PhRvA..52..917A. doi : 10.1103/PhysRevA.52.R917. PMID 9912436.
- ^ Larochelle, S.; Talebpour, A.; Chin, SL (1998). "Непоследовательная многократная ионизация атомов инертного газа в поле лазера Ti:Sapphire". Journal of Physics B: Atomic, Molecular and Optical Physics . 31 (6): 1201. Bibcode : 1998JPhB...31.1201L. doi : 10.1088/0953-4075/31/6/008. S2CID 250747225.
- ^ Fittinghoff, DN; Bolton, PR; Chang, B.; Kulander, KC (1992). «Наблюдение непоследовательной двойной ионизации гелия с помощью оптического туннелирования». Physical Review Letters . 69 (18): 2642–2645. Bibcode :1992PhRvL..69.2642F. doi :10.1103/PhysRevLett.69.2642. PMID 10046547.
- ^ [1] Кучиев, М. Ю. (1987). «Атомная антенна». Письма в ЖЭТФ . 45 : 404–406.
- ^ Schafer, KJ; Yang, B.; DiMauro, LF; Kulander, KC (1992). «Ионизация выше порога за пределами высокой гармоники». Physical Review Letters . 70 (11): 1599–1602. Bibcode : 1993PhRvL..70.1599S. doi : 10.1103/PhysRevLett.70.1599. PMID 10053336.
- ^ Corkum, PB (1993). «Плазменная перспектива многофотонной ионизации в сильном поле». Physical Review Letters . 71 (13): 1994–1997. Bibcode : 1993PhRvL..71.1994C. doi : 10.1103/PhysRevLett.71.1994. PMID 10054556. S2CID 29947935.
- ^ Беккер, Андреас; Фейсал, Фархад ХМ (1996). «Механизм двойной ионизации гелия, индуцированной лазером». Журнал физики B: атомная, молекулярная и оптическая физика . 29 (6): L197–L202. Bibcode : 1996JPhB...29L.197B. doi : 10.1088/0953-4075/29/6/005. ISSN 0953-4075. S2CID 250808704.
- ^ [2] Faisal, FHM; Becker, A. (1997). "Непоследовательная двойная ионизация: механизм и модельная формула". Laser Phys . 7 : 684.
- ^ Уокер, Б.; Шихи, Б.; Димауро, Л. Ф.; Агостини, П.; Шефер, К. Дж.; Куландер, К. К. (1994). «Точное измерение двойной ионизации гелия в сильном поле». Physical Review Letters . 73 (9): 1227–1230. Bibcode :1994PhRvL..73.1227W. doi :10.1103/PhysRevLett.73.1227. PMID 10057657.
- ^ Беккер, А.; Фейсал, ФХМ (1999). "Анализ S-матрицы выходов ионизации атомов благородных газов в фокусе импульсов лазера на титане: сапфире". Журнал физики B: атомная, молекулярная и оптическая физика . 32 (14): L335. Bibcode : 1999JPhB...32L.335B. doi : 10.1088/0953-4075/32/14/101. S2CID 250766534.
- ^ Talebpour, A.; Bandrauk, AD; Yang, J; Chin, SL (1999). "Многофотонная ионизация внутренних валентных электронов и фрагментация этилена в интенсивном импульсе лазера на титане и сапфире" (PDF) . Chemical Physics Letters . 313 (5–6): 789. Bibcode :1999CPL...313..789T. doi :10.1016/S0009-2614(99)01075-1. Архивировано из оригинала (PDF) 21 ноября 2014 г.
- ^ Talebpour, A; Bandrauk, AD; Vijayalakshmi, K; Chin, SL (2000). "Диссоциативная ионизация бензола в интенсивных сверхбыстрых лазерных импульсах". Journal of Physics B: Atomic, Molecular and Optical Physics . 33 (21): 4615. Bibcode : 2000JPhB...33.4615T. doi : 10.1088/0953-4075/33/21/307. S2CID 250738396.
- ^ Мехди Шарифи, С.; Талебпур, А.; Чин, С.Л. (2008). «Сверхбыстрые лазерные импульсы обеспечивают источник ионов для высокоселективной масс-спектроскопии». Applied Physics B. 91 ( 3–4): 579. Bibcode : 2008ApPhB..91..579M. doi : 10.1007/s00340-008-3038-y. S2CID 122546433.
- ^ Пэн, Цзяхуэй; Пушкаш, Ноа; Коркум, Пол Б.; Рейнер, Дэвид М.; Лобода, Александр В. (2012). «Масс-спектрометрия с фемтосекундной лазерной ионизацией в газовой фазе высокого давления». Аналитическая химия . 84 (13): 5633–5640. doi :10.1021/ac300743k. ISSN 0003-2700. PMID 22670784. S2CID 10780362.
- ^ Гаврила, Михай (28.09.2002). «Атомная стабилизация в сверхинтенсивных лазерных полях». Журнал физики B: атомная, молекулярная и оптическая физика . 35 (18): R147–R193. doi :10.1088/0953-4075/35/18/201. ISSN 0953-4075.
- ^ Гаврила, Михай. «Атомная структура и распад в высокочастотных полях». Атомы в интенсивных лазерных полях, под редакцией Михая Гаврилы, Academic Press, Inc, 1992, стр. 435-508.





















![{\displaystyle N=[n_{i}+n_{\mathrm {osc} }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cf3511158ea52a978a39fa7683e7d259b1678e6)




























