Биологическая модель нейрона
В этой статье есть несколько проблем. Помогите улучшить ее или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти сообщения )
|

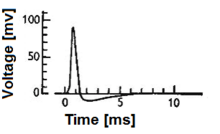
Биологические модели нейронов , также известные как модели спайковых нейронов , [1] являются математическими описаниями проводимости электрических сигналов в нейронах . Нейроны (или нервные клетки) являются электрически возбудимыми клетками в нервной системе , способными посылать электрические сигналы, называемые потенциалами действия , через нейронную сеть. Эти математические модели описывают роль биофизических и геометрических характеристик нейронов в проводимости электрической активности.
Центральным в этих моделях является описание того, как мембранный потенциал (то есть разница в электрическом потенциале между внутренней и внешней частью биологической клетки ) через клеточную мембрану изменяется с течением времени. В экспериментальной обстановке стимуляция нейронов электрическим током генерирует потенциал действия (или спайк), который распространяется по аксону нейрона . Этот аксон может разветвляться и соединяться с большим количеством нижестоящих нейронов в местах, называемых синапсами . В этих синапсах спайк может вызывать высвобождение нейротрансмиттеров , которые, в свою очередь, могут изменять потенциал напряжения нижестоящих нейронов. Это изменение может потенциально привести к еще большему количеству спайков в этих нижестоящих нейронах, таким образом передавая сигнал. Около 95% нейронов в неокортексе , самом внешнем слое мозга млекопитающих , состоят из возбуждающих пирамидальных нейронов , [2] [3], и каждый пирамидальный нейрон получает десятки тысяч входных сигналов от других нейронов. [4] Таким образом, импульсные нейроны являются основным блоком обработки информации нервной системы .
Одним из таких примеров модели нейрона со спайками может быть высокодетализированная математическая модель, включающая пространственную морфологию . Другой может быть модель нейрона на основе проводимости, которая рассматривает нейроны как точки и описывает динамику мембранного напряжения как функцию трансмембранных токов. Математически более простая модель «интегрировать-и-срабатывать» значительно упрощает описание динамики ионного канала и мембранного потенциала (первоначально изученная Лапиком в 1907 году). [5] [6]
Биологическое обоснование, классификация и цели нейронных моделей
Непиковые клетки, пиковые клетки и их измерение
Не все клетки нервной системы производят тип спайка, который определяет область действия моделей спайковых нейронов. Например, волосковые клетки улитки , рецепторные клетки сетчатки и биполярные клетки сетчатки не производят спайков. Более того, многие клетки нервной системы не классифицируются как нейроны, а вместо этого классифицируются как глия .
Активность нейронов можно измерить с помощью различных экспериментальных методов, таких как метод измерения «целой клетки», который фиксирует импульсную активность отдельного нейрона и создает потенциалы действия полной амплитуды.
При внеклеточных методах измерения один или несколько электродов помещаются во внеклеточное пространство . Шипы, часто от нескольких источников, в зависимости от размера электрода и его близости к источникам, могут быть идентифицированы с помощью методов обработки сигнала. Внеклеточные измерения имеют несколько преимуществ:
- Его легче получить экспериментальным путем;
- Он прочный и служит дольше;
- Он может отражать доминирующий эффект, особенно при проведении в анатомической области с большим количеством схожих клеток.
Обзор моделей нейронов
Модели нейронов можно разделить на две категории в соответствии с физическими единицами интерфейса модели. Каждая категория может быть далее разделена в соответствии с уровнем абстракции/детализации:
- Модели электрического входного-выходного мембранного напряжения – эти модели производят прогноз для выходного мембранного напряжения как функции электрической стимуляции, заданной как входной ток или напряжение. Различные модели в этой категории отличаются точной функциональной связью между входным током и выходным напряжением и уровнем детализации. Некоторые модели в этой категории предсказывают только момент возникновения выходного скачка (также известного как «потенциал действия»); другие модели более подробны и учитывают субклеточные процессы. Модели в этой категории могут быть как детерминированными, так и вероятностными.
- Модели нейронов с естественным стимулом или фармакологическим входом – Модели в этой категории связывают входной стимул, который может быть как фармакологическим, так и естественным, с вероятностью события спайка. Входной этап этих моделей не является электрическим, а имеет либо фармакологические (химические) единицы концентрации, либо физические единицы, которые характеризуют внешний стимул, такой как свет, звук или другие формы физического давления. Более того, выходной этап представляет вероятность события спайка, а не электрическое напряжение.
Хотя в науке и технике не редкость иметь несколько описательных моделей для разных уровней абстракции/детализации, количество различных, иногда противоречащих друг другу, биологических моделей нейронов исключительно велико. Эта ситуация отчасти является результатом множества различных экспериментальных установок и трудности отделения внутренних свойств одного нейрона от эффектов измерения и взаимодействий многих клеток ( сетевых эффектов).
Цели нейронных моделей
В конечном счете, биологические модели нейронов направлены на объяснение механизмов, лежащих в основе работы нервной системы. Однако можно выделить несколько подходов: от более реалистичных моделей (например, механистических моделей) до более прагматичных моделей (например, феноменологических моделей). [7] [ необходим лучший источник ] Моделирование помогает анализировать экспериментальные данные и решать вопросы. Модели также важны в контексте восстановления утраченной функциональности мозга с помощью нейропротезных устройств.
Модели электрического входного-выходного мембранного напряжения
Модели в этой категории описывают связь между нейронными мембранными токами на входном этапе и мембранным напряжением на выходном этапе. Эта категория включает (обобщенные) модели интеграции и активации и биофизические модели, вдохновленные работой Ходжкина-Хаксли в начале 1950-х годов с использованием экспериментальной установки, которая прокалывала клеточную мембрану и позволяла нагнетать определенное мембранное напряжение/ток. [8] [9] [10] [11]
Большинство современных электрических нейронных интерфейсов применяют внеклеточную электрическую стимуляцию, чтобы избежать прокола мембраны, который может привести к гибели клеток и повреждению тканей. Следовательно, неясно, в какой степени электрические нейронные модели применимы к внеклеточной стимуляции (см., например, [12] ).
Ходжкин–Хаксли
| Свойство модели H&H | Ссылки |
|---|---|
| Форма отдельного шипа | [8] [9] [10] [11] |
| Идентификация ионов, участвующих в реакции | [8] [9] [10] [11] |
| Скорость распространения импульса по аксону | [8] |
Модель Ходжкина–Хаксли (модель H&H) [8] [9] [10] [11] представляет собой модель взаимосвязи между потоком ионных токов через клеточную мембрану нейрона и мембранным напряжением клетки. [8] [9] [10] [11] Она состоит из набора нелинейных дифференциальных уравнений, описывающих поведение ионных каналов, которые пронизывают клеточную мембрану гигантского аксона кальмара . За эту работу Ходжкин и Хаксли были удостоены Нобелевской премии по физиологии и медицине 1963 года.
Важно отметить зависимость между напряжением и током, при этом множественные токи, зависящие от напряжения, заряжают клеточную мембрану емкостью C· m.
Вышеуказанное уравнение является производной по времени закона емкости , Q = CV , где изменение общего заряда должно быть объяснено как сумма по токам. Каждый ток определяется как
где g ( t , V ) - проводимость или обратное сопротивление, которое может быть расширено с точки зрения его максимальной проводимости ḡ и фракций активации и инактивации m и h , соответственно, которые определяют, сколько ионов может протекать через доступные мембранные каналы. Это расширение задается как
и наши фракции следуют кинетике первого порядка
с аналогичной динамикой для h , где мы можем использовать либо τ и m ∞ , либо α и β для определения наших фракций вентиля.
Модель Ходжкина–Хаксли может быть расширена для включения дополнительных ионных токов. Обычно они включают входящие токи Ca 2+ и Na + , а также несколько разновидностей исходящих токов K + , включая ток «утечки».
Результат может быть на малом конце 20 параметров, которые необходимо оценить или измерить для точной модели. В модели сложной системы нейронов численная интеграция уравнений является вычислительно дорогой . Поэтому необходимы осторожные упрощения модели Ходжкина–Хаксли.
Модель может быть сведена к двум измерениям благодаря динамическим связям, которые могут быть установлены между переменными управления. [13] Также возможно расширить ее, чтобы учесть эволюцию концентраций (считавшихся фиксированными в исходной модели). [14] [15]
Идеальное интегрировать-и-уволить
Одной из самых ранних моделей нейрона является идеальная модель «интегрировать и срабатывать» (также называемая моделью «интегрировать и срабатывать без утечки»), впервые исследованная в 1907 году Луи Лапиком . [16] Нейрон представлен мембранным напряжением V , которое изменяется во времени во время стимуляции входным током I(t) в соответствии с
что является просто производной по времени закона емкости , Q = CV . При подаче входного тока мембранное напряжение увеличивается со временем, пока не достигнет постоянного порогового значения V th , в этот момент происходит всплеск дельта-функции , и напряжение сбрасывается до своего остаточного потенциала, после чего модель продолжает работать. Таким образом, частота срабатывания модели увеличивается линейно без ограничений по мере увеличения входного тока.
Модель можно сделать более точной, введя рефрактерный период t ref , который ограничивает частоту срабатывания нейрона, предотвращая его срабатывание в течение этого периода. Для постоянного входного сигнала I(t)=I пороговое напряжение достигается после времени интегрирования t int =CV thr /I после старта с нуля. После сброса рефрактерный период вводит мертвое время, так что общее время до следующего срабатывания равно t ref + t int . Частота срабатывания является обратной величиной общего интервала между спайками (включая мертвое время). Частота срабатывания как функция постоянного входного тока, таким образом,
Недостатком этой модели является то, что она не описывает ни адаптацию, ни утечку. Если модель получает короткий импульс тока ниже порогового значения в какой-то момент, она сохранит это повышение напряжения навсегда — до тех пор, пока другой входной сигнал позже не заставит ее активироваться. Эта характеристика не соответствует наблюдаемому поведению нейронов. Следующие расширения делают модель интеграции и активации более правдоподобной с биологической точки зрения.
Утечка интегрировать-и-сжечь
Текучая модель интеграции и возгорания, которая восходит к Луи Лапику , [16] содержит термин «утечка» в уравнении мембранного потенциала, который отражает диффузию ионов через мембрану, в отличие от нетекучей модели интеграции и возгорания. Уравнение модели выглядит как [1]
.jpg/440px-Leaky_Integrate-and-Fire_model_neuron_(schematic).jpg)
где V m — напряжение на клеточной мембране, а R m — сопротивление мембраны. (Непротекающая модель «интегрируй и срабатывай» восстанавливается в пределе R m до бесконечности, т. е. если мембрана является идеальным изолятором). Уравнение модели справедливо для произвольного зависящего от времени входа до тех пор, пока не будет достигнуто пороговое значение V th ; после этого мембранный потенциал сбрасывается.
Для постоянного входа минимальный вход для достижения порога равен I th = V th / R m . Предполагая сброс до нуля, частота срабатывания, таким образом, выглядит как
которая сходится для больших входных токов к предыдущей модели без утечек с рефрактерным периодом. [17] Модель также может быть использована для тормозных нейронов. [18] [19]
Самым существенным недостатком этой модели является то, что она не содержит нейронной адаптации, поэтому она не может описать экспериментально измеренную серию спайков в ответ на постоянный входной ток. [20] Этот недостаток устраняется в обобщенных моделях интеграции и активации, которые также содержат одну или несколько переменных адаптации и способны предсказывать время спайков корковых нейронов при подаче тока с высокой степенью точности. [21] [22] [23]
Адаптивная интеграция и запуск
| Адаптивная модель «интегрируй и запускай» | Ссылки |
|---|---|
| Подпороговое напряжение для входного тока, зависящего от времени | [22] [23] |
| Время срабатывания для входного тока, зависящего от времени | [22] [23] |
| Модели срабатывания в ответ на ступенчатый входной ток | [24] [25] [26] |
Нейрональная адаптация относится к тому факту, что даже при наличии постоянного тока инъекции в сому, интервалы между выходными спайками увеличиваются. Адаптивная модель нейрона интеграции и запуска объединяет утечку интеграции напряжения Vс одной или несколькими переменными адаптации w k (см. главу 6.1. в учебнике «Нейронная динамика» [27] )
где - постоянная времени мембраны, w k - номер тока адаптации, с индексом k , - постоянная времени тока адаптации w k , E m - потенциал покоя, а t f - время срабатывания нейрона, а греческая дельта обозначает дельта-функцию Дирака. Всякий раз, когда напряжение достигает порога срабатывания, напряжение сбрасывается до значения V r ниже порога срабатывания. Значение сброса является одним из важных параметров модели. Простейшая модель адаптации имеет только одну переменную адаптации wи сумма по k удаляется. [28]

Интеграционно-активные нейроны с одной или несколькими адаптационными переменными могут объяснять различные паттерны нейронной активации в ответ на постоянную стимуляцию, включая адаптацию, всплеск и начальный всплеск. [24] [25] [26] Более того, адаптивные интеграционно-активные нейроны с несколькими адаптационными переменными способны предсказывать время спайков корковых нейронов при зависящей от времени инъекции тока в сому. [22] [23]
Интеграция-и-запуск с утечкой дробного порядка
Недавние достижения в вычислительном и теоретическом дробном исчислении привели к новой форме модели, называемой Fractional-order leaky integrated-and-fire. [29] [30] Преимущество этой модели в том, что она может фиксировать эффекты адаптации с помощью одной переменной. Модель имеет следующий вид [30]
Как только напряжение достигает порогового значения, оно сбрасывается. Дробное интегрирование использовалось для учета нейронной адаптации в экспериментальных данных. [29]
«Экспоненциальная интеграция-и-срабатывание» и «адаптивная экспоненциальная интеграция-и-срабатывание»
| Адаптивный экспоненциальный интегратор-и-запуск | Ссылки |
|---|---|
| Подпороговое отношение тока к напряжению | [31] |
| Модели срабатывания в ответ на ступенчатый входной ток | [26] |
| Рефрактерность и адаптация | [32] |
В экспоненциальной модели «интегрируй и активируй» [33] генерация спайков происходит экспоненциально, следуя уравнению:
где — мембранный потенциал, — порог внутреннего мембранного потенциала, — постоянная времени мембраны, — потенциал покоя, — острота инициации потенциала действия, обычно около 1 мВ для пирамидальных нейронов коры. [31] Как только мембранный потенциал пересекает , он расходится до бесконечности за конечное время. [34] При численном моделировании интегрирование останавливается, если мембранный потенциал достигает произвольного порога (намного большего, чем ), при котором мембранный потенциал сбрасывается до значения V r . Значение сброса напряжения V r является одним из важных параметров модели. Важно, что правая часть приведенного выше уравнения содержит нелинейность, которая может быть напрямую извлечена из экспериментальных данных. [31] В этом смысле экспоненциальная нелинейность убедительно подтверждается экспериментальными доказательствами.
В адаптивном экспоненциальном интегрирующем и активизирующем нейроне [32] указанная выше экспоненциальная нелинейность уравнения напряжения объединяется с переменной адаптации w

где жобозначает ток адаптации с временной шкалой . Важными параметрами модели являются значение сброса напряжения V r , внутренний порог , постоянные времени и , а также параметры связи aи б. Адаптивная экспоненциальная модель «интегрировать и сработать» наследует экспериментально полученную нелинейность напряжения [31] экспоненциальной модели «интегрировать и сработать». Но, выходя за рамки этой модели, она также может учитывать различные паттерны нейронной активации в ответ на постоянную стимуляцию, включая адаптацию, всплеск и начальный всплеск. [26] Однако, поскольку адаптация имеет форму тока, может возникнуть аберрантная гиперполяризация. Эта проблема была решена путем выражения ее как проводимости. [35]
Модель адаптивного порогового нейрона
В этой модели функция, зависящая от времени, добавляется к фиксированному порогу, , после каждого скачка, вызывая адаптацию порога. Пороговый потенциал, , постепенно возвращается к своему стационарному значению в зависимости от постоянной времени адаптации порога . [36] Это один из самых простых методов достижения адаптации частоты скачков. [37] Выражение для адаптивного порога имеет вид:
где определяется как:
Когда мембранный потенциал достигает порогового значения, он сбрасывается до :
Более простая версия этого подхода с единственной постоянной времени в пороговом затухании с использованием нейрона LIF реализована в [38] для достижения LSTM-подобных рекуррентных импульсных нейронных сетей с целью достижения точности, близкой к ANN, в нескольких пространственно-временных задачах.
Двойной экспоненциальный адаптивный порог (DEXAT)
Модель нейрона DEXAT является разновидностью адаптивной модели нейрона, в которой пороговое напряжение затухает с двойной экспонентой, имеющей две временные константы. Двойной экспоненциальный затухание регулируется быстрым начальным затуханием, а затем более медленным затуханием в течение более длительного периода времени. [39] [40] Этот нейрон, используемый в SNN через суррогатный градиент, создает адаптивную скорость обучения, обеспечивающую более высокую точность и более быструю сходимость, а также гибкую долгосрочную кратковременную память по сравнению с существующими аналогами в литературе. Динамика мембранного потенциала описывается с помощью уравнений, а правило пороговой адаптации следующее:
Динамика и задается выражением
,
,
где и .
Далее, в [41] показана многомасштабная адаптивная пороговая нейронная модель, демонстрирующая более сложную динамику.
Стохастические модели мембранного напряжения и времени импульса
Модели в этой категории являются обобщенными моделями «интегрируй и запускай», которые включают определенный уровень стохастичности. Кортикальные нейроны в экспериментах обнаруживают, что они надежно реагируют на зависящий от времени ввод, хотя и с небольшой степенью вариаций между одним испытанием и следующим, если один и тот же стимул повторяется. [42] [43] Стохастичность в нейронах имеет два важных источника. Во-первых, даже в очень контролируемом эксперименте, где входной ток вводится непосредственно в сому, ионные каналы открываются и закрываются стохастически [44] , и этот шум канала приводит к небольшой изменчивости точного значения мембранного потенциала и точного времени выходных скачков. Во-вторых, для нейрона, встроенного в кортикальную сеть, трудно контролировать точный ввод, потому что большинство вводов поступают от ненаблюдаемых нейронов где-то еще в мозге. [27]
Стохастичность была введена в модели нейронов со спайками в двух принципиально разных формах: либо (i) шумный входной ток добавляется к дифференциальному уравнению модели нейрона; [45] либо (ii) процесс генерации спайков является шумным. [46] В обоих случаях математическая теория может быть разработана для непрерывного времени, которое затем, при желании для использования в компьютерном моделировании, преобразуется в модель с дискретным временем.
Связь шума в нейронных моделях с изменчивостью последовательностей импульсов и нейронных кодов обсуждается в книге «Нейронное кодирование» и в главе 7 учебника «Нейронная динамика». [27]
Модель шумного входа (диффузный шум)
Нейрон, встроенный в сеть, получает импульсный вход от других нейронов. Поскольку время прибытия импульса не контролируется экспериментатором, его можно считать стохастическим. Таким образом, (потенциально нелинейная) модель «интегрировать и запустить» с нелинейностью f(v) получает два входа: вход, контролируемый экспериментатором, и шумовой входной ток , описывающий неконтролируемый фоновый вход.
Модель Стайна [45] является частным случаем текуче-интегрирующего и срабатывающего нейрона и стационарного белого шума со средним нулевым и единичной дисперсией. В подпороговом режиме эти предположения приводят к уравнению процесса Орнштейна–Уленбека
Однако, в отличие от стандартного процесса Орнштейна-Уленбека, мембранное напряжение сбрасывается всякий раз, когда V достигает порога срабатывания V th . [45] Расчет распределения интервалов модели Орнштейна-Уленбека для постоянного входа с порогом приводит к проблеме времени первого прохождения . [45] [47] Модель нейрона Штейна и ее варианты использовались для подгонки распределений интервалов между импульсами серий импульсов от реальных нейронов при постоянном входном токе. [47]
В математической литературе приведенное выше уравнение процесса Орнштейна–Уленбека записывается в виде
где амплитуда входного шума, а dW — приращения винеровского процесса. Для дискретных реализаций с шагом времени dt обновления напряжения равны [27]
где y взято из гауссовского распределения с нулевой средней единичной дисперсией. Напряжение сбрасывается, когда достигает порога срабатывания V th .
Модель шумного входа также может использоваться в обобщенных моделях «интегрировать и сработать». Например, экспоненциальная модель «интегрировать и сработать» с шумным входом читает
Для постоянного детерминированного входа можно рассчитать среднюю частоту срабатывания как функцию . [48] Это важно, поскольку зависимость частоты от тока (кривая fI) часто используется экспериментаторами для характеристики нейрона.
Утечка «интегрировать и активировать» с шумным входом широко использовалась при анализе сетей импульсных нейронов. [49] Шумной вход также называется «диффузным шумом», поскольку он приводит к диффузии подпорогового мембранного потенциала вокруг траектории без шума (Йоханнесма, [50] Теория импульсных нейронов с шумным входом рассматривается в главе 8.2 учебника «Нейронная динамика» . [27]
Модель шумного выхода (шум выхода)
В детерминированных моделях «интегрируй и активируй» всплеск генерируется, если мембранный потенциал V (t)достигает порога . В шумных выходных моделях строгий порог заменяется шумным следующим образом. В каждый момент времени t, спайк генерируется стохастически с мгновенной стохастической интенсивностью или «скоростью выхода» [27]
которая зависит от мгновенной разницы между напряжением мембраны V (t)и порог . [46] Обычный выбор для «скорости побега» (которая согласуется с биологическими данными [22] ) —
.jpg/440px-Spike_Response_Model_with_escape_noise_(noisy_output).jpg)
где — постоянная времени, описывающая, как быстро срабатывает спайк, как только мембранный потенциал достигает порога, и параметр резкости. Поскольку порог становится острым, а спайковая активация происходит детерминированно в тот момент, когда мембранный потенциал достигает порога снизу. Значение резкости, найденное в экспериментах [22] , равно , что означает, что нейронная активация становится существенной, как только мембранный потенциал становится на несколько мВ ниже формального порога активации.
Процесс выхода из состояния с помощью мягкого порога рассматривается в главе 9 учебника « Нейронная динамика». [27]
Для моделей в дискретном времени всплеск генерируется с вероятностью
который зависит от мгновенной разницы между напряжением мембраны Vв момент времени и порог . [55] Функция F часто принимается как стандартная сигмоидальная с параметром крутизны , [46] аналогично динамике обновления в искусственных нейронных сетях. Но функциональная форма F также может быть получена из стохастической интенсивности в непрерывном времени, введенной выше, как где - пороговое расстояние. [46]
Модели «интегрируй и активируй» с выходным шумом можно использовать для прогнозирования гистограммы перистимульного времени (PSTH) реальных нейронов при произвольном, зависящем от времени входе. [22] Для неадаптивных нейронов «интегрируй и активируй» распределение интервалов при постоянной стимуляции можно рассчитать с помощью теории стационарного обновления . [27]
Модель реакции на спайк (SRM)
| Модель реакции на спайк | Ссылки |
|---|---|
| Подпороговое напряжение для входного тока, зависящего от времени | [23] [22] |
| Время срабатывания для входного тока, зависящего от времени | [23] [22] |
| Модели срабатывания в ответ на ступенчатый входной ток | [56] [57] |
| Распределение межспайковых интервалов | [56] [46] |
| Спайк-послепотенциал | [23] |
| рефрактерность и динамический порог срабатывания | [23] [22] |
основная статья : Модель реакции на спайк
Модель реакции на спайк (SRM) представляет собой обобщенную линейную модель для подпорогового мембранного напряжения в сочетании с нелинейным процессом выходного шума для генерации спайка. [46] [58] [56] Напряжение на мембране V (t)в момент времени t есть
где t f — время срабатывания спайка номер f нейрона, V rest — напряжение покоя при отсутствии входа, I(ts)— входной ток в момент времени ts и представляет собой линейный фильтр (также называемый ядром), который описывает вклад импульса входного тока в момент времени ts в напряжение в момент времени t. Вклады в напряжение, вызванные скачком в момент времени, описываются рефрактерным ядром . В частности, описывает сброс после скачка и временной ход потенциала после скачка, следующего за скачком. Таким образом, он выражает последствия рефрактерности и адаптации. [46] [23] Напряжение V(t) можно интерпретировать как результат интеграции дифференциального уравнения модели с утечкой, интегрированной и активированной, связанной с произвольным числом переменных адаптации, запускаемых скачком. [24]
Спайковая активация является стохастической и происходит со стохастической интенсивностью, зависящей от времени (мгновенная скорость).
с параметрами и и динамическим порогом, заданным как
Здесь порог срабатывания неактивного нейрона и описывает увеличение порога после спайка в момент времени . [22] [23] В случае фиксированного порога задается . Для порогового процесса это детерминированный процесс. [27]
Временной ход фильтров, характеризующих модель реакции на спайк, можно напрямую извлечь из экспериментальных данных. [23] С оптимизированными параметрами SRM описывает временной ход подпорогового мембранного напряжения для зависящего от времени входа с точностью 2 мВ и может предсказать время большинства выходных спайков с точностью 4 мс. [22] [23] SRM тесно связана с линейно-нелинейно-пуассоновскими каскадными моделями (также называемыми обобщенной линейной моделью). [54] Оценка параметров вероятностных нейронных моделей, таких как SRM, с использованием методов, разработанных для обобщенных линейных моделей [59], обсуждается в главе 10 учебника Neuronal Dynamics . [27]
.jpg/440px-Spike_Response_Model_(schematic).jpg)
Название модели импульсного отклика возникло потому, что в сети входной ток для нейрона i генерируется импульсами других нейронов, так что в случае сети уравнение напряжения становится
где - время срабатывания нейрона j (т. е. его последовательность спайков); описывает временной ход спайка и потенциал после спайка для нейрона i; и и описывает амплитуду и временной ход возбуждающего или тормозного постсинаптического потенциала (PSP), вызванного спайком пресинаптического нейрона j. Временной ход PSP является результатом свертки постсинаптического тока , вызванного прибытием пресинаптического спайка от нейрона j с мембранным фильтром . [27]
СРМ0
SRM 0 [56] [60] [61] — это стохастическая нейронная модель , связанная с зависящей от времени нелинейной теорией восстановления и упрощением модели реакции на спайк (SRM). Главное отличие от уравнения напряжения SRM, представленного выше, заключается в том, что в члене, содержащем рефрактерное ядро, нет знака суммирования по прошлым спайкам: имеет значение только самый последний спайк (обозначаемый как время ). Другое отличие заключается в том, что порог является постоянным. Модель SRM0 может быть сформулирована в дискретном или непрерывном времени. Например, в непрерывном времени уравнение одного нейрона имеет вид
и уравнения сети SRM 0 [56 ]
где - время последнего срабатывания нейрона i. Обратите внимание, что временной ход постсинаптического потенциала также может зависеть от времени с момента последнего спайка нейрона i, чтобы описать изменение проводимости мембраны во время рефрактерности. [60] Мгновенная скорость срабатывания (стохастическая интенсивность) равна
где - фиксированный порог срабатывания. Таким образом, срабатывание нейрона i зависит только от его входа и времени, прошедшего с момента последнего срабатывания нейрона i.
С помощью SRM 0 распределение интервалов между импульсами для постоянного входного сигнала может быть математически связано с формой рефрактерного ядра . [46] [56] Более того, стационарное отношение частоты к току может быть рассчитано из скорости выхода в сочетании с рефрактерным ядром . [46] [56] При соответствующем выборе ядер SRM 0 приближает динамику модели Ходжкина-Хаксли с высокой степенью точности. [60] Более того, можно предсказать реакцию PSTH на произвольный зависящий от времени входной сигнал. [56]
Модель Гальвеса–Лёхербаха

Модель Гальвеса –Лёхербаха [62] является стохастической нейронной моделью, тесно связанной с моделью реакции спайка SRM 0 [61] [56] и моделью интеграции и срабатывания с утечкой. Она по своей сути стохастическая и, как и SRM 0 , связана с зависящей от времени нелинейной теорией восстановления . Учитывая спецификации модели, вероятность того, что данный нейрон срабатывает спайк в периоде, может быть описана как
где - синаптический вес , описывающий влияние нейрона на нейрон , выражает утечку и обеспечивает историю спайков нейрона до этого , согласно
Важно отметить, что вероятность скачка нейрона зависит только от его входного скачка (отфильтрованного с помощью ядра и взвешенного с помощью коэффициента ) и времени его последнего выходного скачка (обобщенного с помощью ).
Дидактические игрушечные модели мембранного напряжения
Модели в этой категории являются сильно упрощенными игрушечными моделями, которые качественно описывают мембранное напряжение как функцию входа. Они в основном используются в дидактических целях при обучении, но не считаются действительными моделями нейронов для крупномасштабных симуляций или подгонки данных.
Фицхью–Нагумо
Радикальные упрощения уравнения Ходжкина-Хаксли были введены Фицхью и Нагумо в 1961 и 1962 годах. Стремясь описать «регенеративное самовозбуждение» с помощью нелинейного мембранного напряжения с положительной обратной связью и восстановление с помощью линейного затворного напряжения с отрицательной обратной связью, они разработали модель, описанную [63]
где мы снова имеем мембраноподобное напряжение и входной ток с более медленным общим напряжением затвора w и экспериментально определенными параметрами a = -0,7, b = 0,8, τ = 1/0,08 . Хотя модель не выводится из биологии, она допускает упрощенную, немедленно доступную динамику, не будучи тривиальным упрощением. [64] Экспериментальная поддержка слаба, но модель полезна как дидактический инструмент для введения динамики генерации спайков посредством анализа фазовой плоскости . См. Главу 7 в учебнике Методы нейронного моделирования . [65]
Моррис–Лекар
В 1981 году Моррис и Лекар объединили модели Ходжкина-Хаксли и Фицхью-Нагумо в модель потенциалзависимого кальциевого канала с калиевым каналом с задержкой выпрямления, представленным
где . [17] Экспериментальная поддержка модели слаба, но модель полезна как дидактический инструмент для введения динамики генерации спайков через фазовый анализ плоскости. См. Главу 7 [66] в учебнике Методы нейронного моделирования . [65]
Двумерная модель нейрона, очень похожая на модель Морриса-Лекара, может быть выведена шаг за шагом, начиная с модели Ходжкина-Хаксли. См. главу 4.2 в учебнике Neuronal Dynamics. [27]
Хиндмарш–Роуз
Основываясь на модели Фицхью–Нагумо, Хиндмарш и Роуз предложили в 1984 году [67] модель нейронной активности, описываемую тремя связанными дифференциальными уравнениями первого порядка:
с r 2 = x 2 + y 2 + z 2 , и r ≈ 10 −2 , так что переменная z изменяется очень медленно. Эта дополнительная математическая сложность допускает большое разнообразие динамического поведения для мембранного потенциала, описываемого переменной x модели, которая включает хаотическую динамику. Это делает модель нейрона Хиндмарша–Роуза очень полезной, поскольку она по-прежнему проста, позволяет качественно описывать множество различных моделей активации потенциала действия, в частности, взрывного характера, наблюдаемого в экспериментах. Тем не менее, она остается игрушечной моделью и не была подогнана под экспериментальные данные. Она широко используется в качестве эталонной модели для динамики взрывного характера. [67]
Тета-модель и квадратичная интеграция-и-уничтожение
Модель тета , или каноническая модель Эрментраута-Копеля типа I, математически эквивалентна квадратичной модели интеграции и срабатывания, которая в свою очередь является приближением к экспоненциальной модели интеграции и срабатывания и модели Ходжкина-Хаксли. Она называется канонической моделью, поскольку является одной из общих моделей для постоянного ввода вблизи точки бифуркации, что означает близость к переходу от молчаливого к повторяющемуся срабатыванию. [68] [69]
Стандартная формулировка тета-модели: [27] [68] [69]
Уравнение для квадратичной модели «интегрировать и сработать» имеет вид (см. главу 5.3 в учебнике «Нейронная динамика» [27] ):
Эквивалентность модели тета и квадратичного интегрирования и активации рассматривается, например, в главе 4.1.2.2 моделей импульсных нейронов. [1]
Для входных данных , которые со временем меняются или находятся далеко от точки бифуркации, предпочтительнее работать с экспоненциальной моделью интеграции и срабатывания (если вы хотите оставаться в классе одномерных моделей нейронов), поскольку реальные нейроны демонстрируют нелинейность экспоненциальной модели интеграции и срабатывания. [31]
Модели нейронов, кодирующих входные сенсорные стимулы
Модели в этой категории были получены в результате экспериментов, включающих естественную стимуляцию, такую как свет, звук, прикосновение или запах. В этих экспериментах паттерн спайков, возникающий в результате каждого предъявления стимула, варьируется от испытания к испытанию, но усредненный ответ от нескольких испытаний часто сходится к четкому паттерну. Следовательно, модели в этой категории генерируют вероятностную связь между входным стимулом и возникновением спайков. Важно, что зарегистрированные нейроны часто располагаются на несколько этапов обработки после сенсорных нейронов, так что эти модели суммируют эффекты последовательности этапов обработки в компактной форме
Модель неоднородного пуассоновского процесса (Зиберта)
Зиберт [70] [71] смоделировал паттерн нейронной импульсации, используя модель неоднородного процесса Пуассона , следуя экспериментам с участием слуховой системы. [70] [71] По мнению Зиберта, вероятность импульсного события в интервале времени пропорциональна неотрицательной функции , где — исходный стимул.:
Зиберт рассматривал несколько функций , в том числе для низких интенсивностей стимула.
Главное преимущество модели Зиберта — ее простота. Недостатком модели является ее неспособность адекватно отражать следующие явления:
- Кратковременное усиление активности нейронов в ответ на ступенчатый стимул.
- Насыщение темпа стрельбы.
- Значения межспайкового интервала - гистограмма при значениях коротких интервалов (близких к нулю).
Эти недостатки устраняются с помощью модели точечного процесса, зависящего от возраста, и двухуровневой модели Маркова. [72] [73] [74]
Модель точечного процесса, зависящего от рефрактерности и возраста
Берри и Мейстер [75] изучали нейронную рефрактерность, используя стохастическую модель, которая предсказывает спайки как произведение двух членов: функции f(s(t)), которая зависит от зависящего от времени стимула s(t), и функции восстановления, которая зависит от времени, прошедшего с момента последнего спайка.
Модель также называется неоднородным интервальным процессом Маркова (IMI) . [76] Подобные модели использовались в течение многих лет в слуховой нейронауке. [77] [78] [79] Поскольку модель сохраняет память о времени последнего спайка, она не является пуассоновской и относится к классу моделей восстановления, зависящих от времени. [27] Она тесно связана с моделью SRM0 с экспоненциальной скоростью ухода. [27] Важно, что можно подогнать параметры модели точечного процесса, зависящего от возраста, таким образом, чтобы описать не только реакцию PSTH, но и статистику интервалов между спайками. [76] [77] [79]
Линейно-нелинейная каскадная модель Пуассона и GLM
Линейно -нелинейно-пуассоновская каскадная модель представляет собой каскад линейного процесса фильтрации, за которым следует нелинейный этап генерации спайков. [80] В случае, когда выходные спайки возвращаются обратно через линейный процесс фильтрации, мы приходим к модели, известной в нейронауках как обобщенная линейная модель (GLM). [54] [59] GLM математически эквивалентна модели реакции спайков (SRM) с шумом выхода; но тогда как в SRM внутренние переменные интерпретируются как мембранный потенциал и порог срабатывания, в GLM внутренние переменные являются абстрактными величинами, которые суммируют чистый эффект ввода (и недавних выходных спайков) до того, как спайки будут сгенерированы на последнем этапе. [27] [54]
Модель Маркова с двумя состояниями (Носсенсон и Мессер)
Модель нейрона спайка Носсенсона и Мессера [72] [73] [74] выдает вероятность того, что нейрон выдаст спайк, как функцию внешнего или фармакологического стимула. [72] [73] [74] Модель состоит из каскада модели рецепторного слоя и модели нейрона спайка, как показано на рис. 4. Связь между внешним стимулом и вероятностью спайка устанавливается в два этапа: сначала модель рецепторной клетки преобразует необработанный внешний стимул в концентрацию нейротрансмиттера, а затем модель нейрона спайка связывает концентрацию нейротрансмиттера со скоростью срабатывания (вероятность спайка). Таким образом, модель нейрона спайка сама по себе зависит от концентрации нейротрансмиттера на входном этапе. [72] [73] [74]


Важной особенностью этой модели является прогнозирование паттерна частоты срабатывания нейронов, который фиксирует, используя небольшое количество свободных параметров, характерный подчеркнутый краем ответ нейронов на стимулирующий импульс, как показано на рис. 5. Частота срабатывания определяется как нормализованная вероятность для срабатывания нейронного спайка и как величина, пропорциональная току нейротрансмиттеров, выделяемых клеткой. Выражение для частоты срабатывания принимает следующий вид:
где,
- P0 — вероятность того, что нейрон «вооружен» и готов к выстрелу. Она определяется следующим дифференциальным уравнением:
P0 обычно можно вычислить рекурсивно с использованием метода Эйлера, но в случае импульса стимула это дает простое выражение в замкнутой форме. [72] [81]
- y ( t ) является входом модели и интерпретируется как концентрация нейротрансмиттера в окружающей клетке (в большинстве случаев глутамата). Для внешнего стимула ее можно оценить с помощью модели рецепторного слоя:
где представляет собой кратковременное среднее значение мощности стимула (выраженное в ваттах или другой энергии за единицу времени).
- R 0 соответствует собственной частоте спонтанной активации нейрона.
- R 1 — скорость восстановления нейрона из рефрактерного состояния.
Другие прогнозы этой модели включают:
1) Усредненный вызванный ответный потенциал (ERP), обусловленный популяцией множества нейронов в нефильтрованных измерениях, напоминает частоту срабатывания. [74]
2) Изменение напряжения активности, вызванное множественной нейронной активностью, напоминает частоту импульсации (также известную как мощность многоэлементной активности или MUA). [73] [74]
3) Распределение вероятностей между интервалами импульсов принимает форму функции, подобной гамма-распределению. [72] [81]
| Собственность модели Nossenson & Messer | Ссылки | Описание экспериментальных данных |
|---|---|---|
| Форма частоты импульсов в ответ на звуковой стимул | [82] [83] [84] [85] [86] | График скорости стрельбы имеет ту же форму, что и на рис. 5. |
| Форма частоты импульсов в ответ на визуальный стимульный импульс | [87] [88] [89] [90] | График скорости стрельбы имеет ту же форму, что и на рис. 5. |
| Форма частоты импульсации в ответ на импульс обонятельного стимула | [91] | График скорости стрельбы имеет ту же форму, что и на рис. 5. |
| Форма частоты импульсации в ответ на соматосенсорный стимул | [92] | График скорости стрельбы имеет ту же форму, что и на рис. 5. |
| Изменение частоты импульсов в ответ на применение нейромедиатора (в основном глутамата) | [93] [94] | Изменение частоты импульсов в ответ на применение нейромедиатора (глутамата) |
| Квадратичная зависимость между давлением слухового стимула и частотой импульсации | [95] | Квадратичная зависимость между давлением слухового стимула и частотой импульсации (- Линейная зависимость в квадрате давления (мощности)). |
| Квадратичная зависимость между электрическим полем зрительного стимула (вольт) и частотой импульсации | [88] | Квадратичная зависимость между электрическим полем зрительного стимула (вольт) - линейная зависимость между силой зрительного стимула и частотой импульсации. |
| Форма статистики межпикового интервала (ISI) | [96] | Форма ISI напоминает гамма-функцию |
| ERP напоминает частоту выстрелов в нефильтрованных измерениях | [97] | Форма усредненного вызванного ответного потенциала в ответ на стимул напоминает частоту импульсации (рис. 5). |
| Мощность MUA напоминает скорострельность | [74] [98] | Форма эмпирической дисперсии внеклеточных измерений в ответ на импульс стимула напоминает частоту импульсации (рис. 5). |
Модели нейронов фармакологического входного стимула
Модели этой категории позволяют делать прогнозы для экспериментов с фармакологической стимуляцией.
Синаптическая передача (Кох и Сегев)
Согласно модели Коха и Сегева [17], реакция нейрона на отдельные нейротрансмиттеры может быть смоделирована как расширение классической модели Ходжкина-Хаксли как со стандартными, так и нестандартными кинетическими токами. Четыре нейротрансмиттера в первую очередь влияют на ЦНС. Рецепторы AMPA/каинат являются быстрыми возбуждающими медиаторами, в то время как рецепторы NMDA опосредуют значительно более медленные токи. Быстрые тормозные токи проходят через рецепторы GABA A , в то время как рецепторы GABA B опосредуются вторичными калиевыми каналами, активируемыми G -белком. Этот диапазон опосредования создает следующую динамику тока:
где ḡ — максимальная [8] [17] проводимость (около 1 S ), а E — равновесный потенциал данного иона или трансмиттера (AMDA, NMDA, Cl или K ), тогда как [ O ] описывает долю открытых рецепторов. Для NMDA существует значительный эффект магниевого блока , который зависит сигмоидально от концентрации внутриклеточного магния по B ( V ) . Для GABA B [ G ] — концентрация G -белка, а K d описывает диссоциацию G при связывании с калиевыми воротами.
Динамика этой более сложной модели хорошо изучена экспериментально и дает важные результаты с точки зрения очень быстрой синаптической потенциации и депрессии , то есть быстрого краткосрочного обучения.
Стохастическая модель Носсенсона и Мессера переводит концентрацию нейротрансмиттера на входном этапе в вероятность высвобождения нейротрансмиттера на выходном этапе. [72] [73] [74] Более подробное описание этой модели см. выше в разделе «Двухуровневая марковская модель».
Модель нейрона HTM
Модель нейрона HTM была разработана Джеффом Хокинсом и исследователями из Numenta и основана на теории под названием «Иерархическая временная память» , первоначально описанной в книге «Об интеллекте» . Она основана на нейронауке , физиологии и взаимодействии пирамидальных нейронов в неокортексе человеческого мозга.
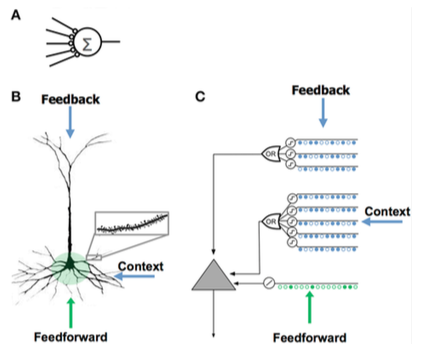
Искусственная нейронная сеть (ИНС) | Пирамидальный нейрон неокортекса (биологический нейрон) | Модель нейрона HTM |
| - Мало синапсов - Дендритов нет - Сумма входных данных x веса - Обучается, изменяя вес синапсов | - Тысячи синапсов на дендритах - Активные дендриты: клетка распознает сотни уникальных паттернов - Совместная активация набора синапсов на дендритном сегменте вызывает спайк NMDA и деполяризацию в соме - Источники поступления в ячейку:
- Обучается, выращивая новые синапсы | - Вдохновлено пирамидальными клетками в слоях неокортекса 2/3 и 5 - Тысячи синапсов - Активные дендриты: клетка распознает сотни уникальных паттернов - Моделирует дендриты и спайки NMDA с каждым массивом совпадающих детекторов, имеющим набор синапсов - Обучается, моделируя рост новых синапсов |
Приложения
Модели нейронных спайков используются в различных приложениях, где требуется кодирование или декодирование последовательностей нейронных спайков в контексте нейропротезов и интерфейсов мозг-компьютер, таких как протез сетчатки : [12] [99] [100] [101] или управление искусственными конечностями и ощущениями. [102] [103] [104] Приложения не являются частью этой статьи; для получения дополнительной информации по этой теме обратитесь к основной статье.
Связь между искусственными и биологическими моделями нейронов
Самая базовая модель нейрона состоит из входа с некоторым вектором синаптического веса и функцией активации или передаточной функцией внутри нейрона, определяющей выход. Это базовая структура, используемая для искусственных нейронов, которая в нейронной сети часто выглядит как
где y i — выход i- го нейрона, x j — входной сигнал j- го нейрона, w ij — синаптический вес (или сила связи) между нейронами i и j , а φ — функция активации . Хотя эта модель показала себя успешной в приложениях машинного обучения, она является плохой моделью для реальных (биологических) нейронов, поскольку в ней отсутствует зависимость от времени на входе и выходе.
Когда вход включается в момент времени t и затем поддерживается постоянным, биологические нейроны испускают серию спайков. Важно отметить, что эта серия спайков не является регулярной, а демонстрирует временную структуру, характеризующуюся адаптацией, всплеском или начальным всплеском, за которым следует регулярный спайк. Обобщенные модели интеграции и активации, такие как адаптивная экспоненциальная модель интеграции и активации, модель реакции на спайк или (линейная) адаптивная модель интеграции и активации, могут улавливать эти паттерны нейронной активации. [24] [25] [26]
Более того, нейронный вход в мозг зависит от времени. Зависящий от времени вход преобразуется сложными линейными и нелинейными фильтрами в серию спайков на выходе. Опять же, модель реакции на спайки или адаптивная модель интеграции и активации позволяет предсказывать серию спайков на выходе для произвольного зависящего от времени входа, [22] [23], тогда как искусственный нейрон или простая утечка интеграции и активации не позволяют.
Если взять модель Ходжкина-Хаксли в качестве отправной точки, то обобщенные модели «интегрировать и запустить» могут быть выведены систематически в пошаговой процедуре упрощения. Это было явно показано для экспоненциальной модели «интегрировать и запустить» [33] и модели спайкового ответа . [60]
В случае моделирования биологического нейрона вместо абстракций, таких как «вес» и «передаточная функция», используются физические аналоги. Нейрон заполнен и окружен ионами, содержащими воду, которые несут электрический заряд. Нейрон связан изолирующей клеточной мембраной и может поддерживать концентрацию заряженных ионов с обеих сторон, которая определяет емкость C m . Возбуждение нейрона включает перемещение ионов в клетку, что происходит, когда нейротрансмиттеры заставляют ионные каналы на клеточной мембране открываться. Мы описываем это физическим током, зависящим от времени I ( t ) . С этим происходит изменение напряжения или разности электрической потенциальной энергии между клеткой и ее окружением, что, как иногда наблюдается, приводит к скачку напряжения, называемому потенциалом действия , который проходит по всей длине клетки и вызывает высвобождение дополнительных нейротрансмиттеров. Напряжение, таким образом, является величиной, представляющей интерес, и задается как V m ( t ) . [19]
Если входной ток постоянен, большинство нейронов испускают после некоторого времени адаптации или первоначального залпа регулярную серию спайков. Частота регулярной активации в ответ на постоянный ток I описывается соотношением частота-ток, которое соответствует передаточной функции искусственных нейронных сетей. Аналогично, для всех моделей спайковых нейронов передаточная функция может быть рассчитана численно (или аналитически).
Теория кабелей и модели отсеков
Все вышеперечисленные детерминированные модели являются моделями точечных нейронов, поскольку они не учитывают пространственную структуру нейрона. Однако дендрит вносит вклад в преобразование входа в выход. [105] [65] Модели точечных нейронов являются допустимым описанием в трех случаях. (i) Если входной ток напрямую вводится в сому. (ii) Если синаптический вход поступает преимущественно в сому или близко к ней (близость определяется шкалой длины, введенной ниже. (iii) Если синапс поступает в любое место дендрита, но дендрит полностью линейный. В последнем случае кабель действует как линейный фильтр; эти свойства линейного фильтра могут быть включены в формулировку обобщенных моделей интеграции и активации, таких как модель реакции спайка .
Свойства фильтра можно рассчитать с помощью уравнения кабеля .
Рассмотрим клеточную мембрану в виде цилиндрического кабеля. Положение на кабеле обозначается как x, а напряжение на клеточной мембране как V. Кабель характеризуется продольным сопротивлением на единицу длины и мембранным сопротивлением . Если все линейно, то напряжение изменяется как функция времени
| 19 |
Вводим масштаб длины на левой стороне и постоянную времени на правой стороне. Теперь уравнение кабеля можно записать в его, возможно, наиболее известной форме:
| 20 |
Приведенное выше уравнение кабеля справедливо для одного цилиндрического кабеля.
Теория линейного кабеля описывает дендритное дерево нейрона как цилиндрическую структуру, подвергающуюся регулярному паттерну бифуркации , подобно ветвям дерева. Для одного цилиндра или целого дерева статическая входная проводимость у основания (где дерево встречается с телом клетки или любой такой границей) определяется как
- ,
где L — электротоническая длина цилиндра, которая зависит от его длины, диаметра и сопротивления. Простой рекурсивный алгоритм масштабируется линейно с числом ветвей и может быть использован для расчета эффективной проводимости дерева. Это определяется как
где A D = πld — общая площадь поверхности дерева общей длины l , а L D — его общая электротоническая длина. Для целого нейрона, в котором проводимость тела клетки равна G S , а проводимость мембраны на единицу площади равна G md = G m / A , мы находим общую проводимость нейрона G N для n деревьев дендритов, суммируя все проводимости дерева и сомы, определяемые как
где мы можем найти общий поправочный коэффициент F dga экспериментально, заметив G D = G md A D F dga .
Линейная кабельная модель делает несколько упрощений, чтобы дать замкнутые аналитические результаты, а именно, что дендритная древовидная структура должна разветвляться в уменьшающихся парах в фиксированном шаблоне и что дендриты являются линейными. Компартментальная модель [65] допускает любую желаемую топологию дерева с произвольными ветвями и длинами, а также произвольными нелинейностями. По сути, это дискретизированная вычислительная реализация нелинейных дендритов.
Каждая часть или отсек дендрита моделируется прямым цилиндром произвольной длины l и диаметра d , который соединяется с фиксированным сопротивлением с любым количеством разветвляющихся цилиндров. Мы определяем отношение проводимости i- го цилиндра как B i = G i / G ∞ , где и R i — сопротивление между текущим отсеком и следующим. Мы получаем ряд уравнений для отношений проводимости в отсеке и из него, внося поправки в нормальную динамику B out, i = B in, i+1 , как
где последнее уравнение имеет дело с родителями и дочерними клетками в ветвях, и . Мы можем итерировать эти уравнения по дереву, пока не получим точку, где дендриты соединяются с телом клетки (сомой), где отношение проводимости равно B in,stem . Тогда наша общая проводимость нейрона для статического входа определяется как
Важно, что статический вход — это очень особый случай. В биологии входы зависят от времени. Более того, дендриты не всегда линейны.
Компартментальные модели позволяют включать нелинейности через ионные каналы, расположенные в произвольных местах вдоль дендритов. [105] [106] Для статических входов иногда можно уменьшить количество компартментов (увеличить скорость вычислений) и при этом сохранить основные электрические характеристики. [107]
Предположения о роли нейрона в более широком контексте принципа работы мозга
Схема обнаружения энергии на основе нейротрансмиттеров
Схема обнаружения энергии на основе нейротрансмиттеров [74] [81] предполагает, что нервная ткань химически выполняет процедуру обнаружения, подобную радару.

Как показано на рис. 6, ключевая идея гипотезы заключается в том, чтобы учитывать концентрацию нейротрансмиттера, генерацию нейротрансмиттера и скорости удаления нейротрансмиттера как важные величины при выполнении задачи обнаружения, при этом ссылаясь на измеренные электрические потенциалы как на побочный эффект, который только в определенных условиях совпадает с функциональным назначением каждого шага. Схема обнаружения похожа на радарное «обнаружение энергии», поскольку включает в себя возведение сигнала в квадрат, временное суммирование и механизм порогового переключения, как и детектор энергии, но также включает в себя блок, который подчеркивает края стимула и переменную длину памяти (переменную память). Согласно этой гипотезе, физиологическим эквивалентом статистики энергетического теста является концентрация нейротрансмиттера, а скорость срабатывания соответствует току нейротрансмиттера. Преимущество этой интерпретации в том, что она приводит к объяснению, согласованному с единицей, которое позволяет навести мосты между электрофизиологическими измерениями, биохимическими измерениями и психофизическими результатами.
Доказательства, рассмотренные в [74] [81], предполагают следующую связь между функциональностью и гистологической классификацией:
- Квадратурирование стимула, скорее всего, осуществляется рецепторными клетками.
- Выделение границ стимула и передача сигнала осуществляются нейронами.
- Временное накопление нейротрансмиттеров осуществляется глиальными клетками. Кратковременное накопление нейротрансмиттеров, вероятно, происходит также в некоторых типах нейронов.
- Логическое переключение осуществляется глиальными клетками и происходит в результате превышения порогового уровня концентрации нейротрансмиттера. Преодоление этого порога также сопровождается изменением скорости утечки нейротрансмиттера.
- Физическое переключение по принципу «все или ничего» происходит благодаря мышечным клеткам и является результатом превышения определенного порога концентрации нейромедиатора в мышечной среде.
Обратите внимание, что хотя электрофизиологические сигналы на рис.6 часто похожи на функциональный сигнал (мощность сигнала/концентрация нейротрансмиттера/мышечная сила), есть некоторые этапы, на которых электрическое наблюдение отличается от функциональной цели соответствующего шага. В частности, Носсенсон и др. предположили, что пересечение порога глии имеет совершенно иную функциональную операцию по сравнению с излучаемым электрофизиологическим сигналом и что последний может быть лишь побочным эффектом разрыва глии.
Общие замечания относительно современной перспективы научных и инженерных моделей
- Модели выше все еще являются идеализациями. Необходимо внести поправки на увеличенную площадь поверхности мембраны, обусловленную многочисленными дендритными шипами, температуры, значительно более высокие, чем экспериментальные данные при комнатной температуре, и неоднородность внутренней структуры клетки. [17] Некоторые наблюдаемые эффекты не вписываются в некоторые из этих моделей. Например, температурный цикл (с минимальным чистым повышением температуры) клеточной мембраны во время распространения потенциала действия несовместим с моделями, которые полагаются на моделирование мембраны как сопротивления, которое должно рассеивать энергию, когда через нее протекает ток. Кратковременное утолщение клеточной мембраны во время распространения потенциала действия также не предсказывается этими моделями, равно как и изменение емкости и скачок напряжения, возникающие в результате этого утолщения, не включены в эти модели. Действие некоторых анестетиков, таких как инертные газы, также проблематично для этих моделей. Новые модели, такие как солитонная модель, пытаются объяснить эти явления, но они менее развиты, чем старые модели, и еще не получили широкого применения.
- Современные взгляды на роль научной модели предполагают, что «Все модели неверны, но некоторые полезны» (Бокс и Дрейпер, 1987, Гриббин, 2009; Панински и др., 2009).
- Недавняя гипотеза предполагает, что каждый нейрон может функционировать как совокупность независимых пороговых единиц. Предполагается, что нейрон может быть анизотропно активирован после происхождения его прибывающих сигналов к мембране через его дендритные деревья. Также предполагалось, что форма волны спайка зависит от происхождения стимула. [108]
Внешние ссылки
- Нейронная динамика: от отдельных нейронов к сетям и моделям познания (В. Герстнер, В. Кистлер, Р. Нод, Л. Панински, Cambridge University Press, 2014) . [27] В частности, главы 6–10, html онлайн-версия.
- Модели импульсных нейронов [1] (В. Герстнер и В. Кистлер, Cambridge University Press, 2002)
Смотрите также
- Связывающий нейрон
- Байесовский подход к функционированию мозга
- Интерфейсы мозг-компьютер
- Принцип свободной энергии
- Модели нейронных вычислений
- Нейронное кодирование
- Нейронные колебания
- Количественные модели потенциала действия
- Шипящая нейронная сеть
Ссылки
- ^ abcd Gerstner W, Kistler WM (2002). Модели спайковых нейронов: отдельные нейроны, популяции, пластичность. Кембридж, Великобритания: Cambridge University Press. ISBN 0-511-07817-X. OCLC 57417395.
- ^ ДеФелипе, Хавьер; Фаринас, Изабель (1992). «Пирамидальный нейрон коры головного мозга: морфологические и химические характеристики синаптических входов». Progress in Neurobiology . 39 (6): 563– 607. doi :10.1016/0301-0082(92)90015-7. PMID 1410442. S2CID 34889543.
- ^ Маркрам, Генри; Мюллер, Эйлиф; Рамасвами, Шрикант; Рейманн, Майкл; Абделла, Марван (2015). «Реконструкция и моделирование неокортикальной микросхемы». Cell . 163 (2): 456– 492. doi : 10.1016/j.cell.2015.09.029 . PMID 26451489. S2CID 14466831.
- ^ Вонг, Р.К.С.; Трауб, Р.Д. (2009-01-01), «СЕТИ | Клеточные свойства и синаптическая связность пирамидальных клеток CA3: механизмы эпилептической синхронизации и эпилептогенеза», в Schwartzkroin, Philip A. (ред.), Encyclopedia of Basic Epilepsy Research , Oxford: Academic Press, стр. 815–819 , doi :10.1016/b978-012373961-2.00215-0, ISBN 978-0-12-373961-2, получено 2020-11-18
- ^ Лапик, LM (1907). «Количественные исследования по электрическому возбуждению нервов». J Физиол Париж . 9 : 620–635 .
- ^ Эбботт, Ларри (1999). «Введение Лапика в модель нейрона «интегрировать и активировать» (1907)». Brain Research Bulletin . 50 (5): 303– 304. doi :10.1016/S0361-9230(99)00161-6. PMID 10643408. S2CID 46170924.
- ^ Голд, Кристоф; Брун, Седрик; Боро, Томас; Карлу, Мэллори; Депаннемекер, Дэмиен (14.01.2022). «Вычислительные модели в нейронауках между механистической и феноменологической характеристиками». doi : 10.20944/preprints202201.0206.v1 . S2CID 246059455.
- ^ abcdefg Hodgkin AL, Huxley AF (август 1952). «Количественное описание мембранного тока и его применение к проводимости и возбуждению в нерве». Журнал физиологии . 117 (4): 500– 44. doi :10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237 .
- ^ abcde Hodgkin AL, Huxley AF, Katz B (апрель 1952 г.). «Измерение отношений тока и напряжения в мембране гигантского аксона Лолиго». Журнал физиологии . 116 (4): 424– 48. doi :10.1113/jphysiol.1952.sp004716. PMC 1392219. PMID 14946712 .
- ^ abcde Hodgkin AL, Huxley AF (апрель 1952 г.). «Токи, переносимые ионами натрия и калия через мембрану гигантского аксона Лолиго». Журнал физиологии . 116 (4): 449–72 . doi :10.1113/jphysiol.1952.sp004717. PMC 1392213. PMID 14946713 .
- ^ abcde Hodgkin AL, Huxley AF (апрель 1952 г.). «Компоненты мембранной проводимости в гигантском аксоне Loligo». Журнал физиологии . 116 (4): 473–96 . doi :10.1113/jphysiol.1952.sp004718. PMC 1392209. PMID 14946714 .
- ^ ab Mathieson K, Loudin J, Goetz G, Huie P, Wang L, Kamins TI и др. (июнь 2012 г.). «Фотоэлектрический ретинальный протез с высокой плотностью пикселей». Nature Photonics . 6 (6): 391– 397. Bibcode :2012NaPho...6..391M. doi :10.1038/nphoton.2012.104. PMC 3462820 . PMID 23049619.
- ^ Ижикевич EM (2010). Динамические системы в нейронауке: геометрия возбудимости и взрывного действия . Кембридж, Массачусетс: MIT Press. ISBN 978-0-262-51420-0. OCLC 457159828.
- ^ Cressman JR, Ullah G, Ziburkus J, Schiff SJ, Barreto E (апрель 2009 г.). «Влияние динамики натрия и калия на возбудимость, судороги и стабильность персистирующих состояний: I. Динамика отдельных нейронов». Journal of Computational Neuroscience . 26 (2): 159– 70. doi :10.1007/s10827-008-0132-4. PMC 2704057 . PMID 19169801.
- ^ Depannemaecker D, Ivanov A, Lillo D, Spek L, Bernard C, Jirsa V (2021-02-17). «Единая физиологическая структура переходов между приступами, устойчивой иктальной активностью и деполяризационным блоком на уровне одного нейрона». bioRxiv : 2020.10.23.352021. doi : 10.1101/2020.10.23.352021 . S2CID 225962412.
- ^ ab Abbott LF (1999). "Введение Лапика в модель нейрона интегративно-активного типа (1907)" (PDF) . Brain Research Bulletin . 50 ( 5– 6): 303– 4. doi :10.1016/S0361-9230(99)00161-6. PMID 10643408. S2CID 46170924. Архивировано из оригинала (PDF) 2007-06-13.
- ^ abcde Кох С., Сегев И. (1999). Методы нейронного моделирования: от ионов к сетям (2-е изд.). Кембридж, Массачусетс: MIT Press. стр. 687. ISBN 978-0-262-11231-4. Архивировано из оригинала 2011-07-07 . Получено 2013-01-10 .
- ^ Брунель Н. (2000-05-01). «Динамика редко связанных сетей возбуждающих и тормозных импульсных нейронов». Журнал вычислительной нейронауки . 8 (3): 183–208 . doi :10.1023/A:1008925309027. PMID 10809012. S2CID 1849650.
- ^ ab Cejnar P, Vyšata O, Kukal J, Beránek M, Vališ M, Procházka A (апрель 2020 г.). "Простая модель конденсаторного переключателя возбуждающего и тормозного нейрона со всеми биологически объясненными частями допускает хаотические колебания, зависящие от паттерна входного сигнала". Scientific Reports . 10 (1): 7353. Bibcode :2020NatSR..10.7353C. doi :10.1038/s41598-020-63834-7. PMC 7192907 . PMID 32355185.
- ^ Fuortes MG, Mantegazzini F (июль 1962). «Интерпретация повторяющегося срабатывания нервных клеток». Журнал общей физиологии . 45 (6): 1163–79 . doi :10.1085/jgp.45.6.1163. PMC 2195242. PMID 13895926 .
- ^ La Camera G, Rauch A, Lüscher HR, Senn W, Fusi S (октябрь 2004 г.). «Минимальные модели адаптированного нейронного ответа на in vivo-подобные входные токи». Neural Computation . 16 (10): 2101– 24. doi :10.1162/0899766041732468. PMID 15333209. S2CID 1428381.
- ^ abcdefghijklmn Jolivet R, Rauch A, Lüscher HR, Gerstner W (август 2006 г.). «Предсказание времени спайка неокортикальных пирамидальных нейронов с помощью простых пороговых моделей». Journal of Computational Neuroscience . 21 (1): 35– 49. doi :10.1007/s10827-006-7074-5. PMID 16633938. S2CID 8911457.
- ^ abcdefghijklmn Pozzorini C, Naud R, Mensi S, Gerstner W (июль 2013 г.). «Временное отбеливание с помощью степенной адаптации в неокортикальных нейронах». Nature Neuroscience . 16 (7): 942– 8. doi :10.1038/nn.3431. PMID 23749146. S2CID 1873019.
- ^ abcd Gerstner W, van Hemmen JL, Cowan JD (ноябрь 1996 г.). «Что имеет значение в нейронной блокировке?». Neural Computation . 8 (8): 1653–76 . doi :10.1162/neco.1996.8.8.1653. PMID 8888612. S2CID 1301248.
- ^ abc Ижикевич EM (ноябрь 2003). "Простая модель импульсных нейронов". IEEE Transactions on Neural Networks . 14 (6): 1569– 72. doi :10.1109/TNN.2003.820440. PMID 18244602. S2CID 814743.
- ^ abcdef Naud R, Marcille N, Clopath C, Gerstner W (ноябрь 2008 г.). «Шаблоны срабатывания в адаптивной экспоненциальной модели интеграции и срабатывания». Biological Cybernetics . 99 ( 4– 5): 335– 47. doi :10.1007/s00422-008-0264-7. PMC 2798047 . PMID 19011922.
- ^ abcdefghijklmnopqr Wulfram Gerstner W, Kistler WM, Naud R, Paninski L (24 июля 2014 г.). Нейронная динамика: от отдельных нейронов к сетям и моделям познания. Кембридж, Великобритания. ISBN 978-1-107-06083-8. OCLC 861774542.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Ричардсон М.Дж., Брунель Н., Хаким В. (май 2003 г.). «От подпорогового до резонанса частоты импульсов». Журнал нейрофизиологии . 89 (5): 2538–54 . doi :10.1152/jn.00955.2002. PMID 12611957.
- ^ ab Lundstrom BN, Higgs MH, Spain WJ, Fairhall AL (ноябрь 2008 г.). «Дробная дифференциация неокортикальными пирамидальными нейронами». Nature Neuroscience . 11 (11): 1335– 42. doi :10.1038/nn.2212. PMC 2596753 . PMID 18931665.
- ^ ab Teka W, Marinov TM, Santamaria F (март 2014 г.). "Адаптация синхронизации нейронных спайков, описанная с помощью дробной модели интеграции и срабатывания с утечкой". PLOS Computational Biology . 10 (3): e1003526. Bibcode : 2014PLSCB..10E3526T. doi : 10.1371/journal.pcbi.1003526 . PMC 3967934. PMID 24675903 .
- ^ abcde Badel L, Lefort S, Brette R, Petersen CC, Gerstner W , Richardson MJ (февраль 2008 г.). «Динамические кривые IV являются надежными предикторами естественных следов напряжения пирамидальных нейронов». Журнал нейрофизиологии . 99 (2): 656– 66. CiteSeerX 10.1.1.129.504 . doi :10.1152/jn.01107.2007. PMID 18057107.
- ^ ab Brette R, Gerstner W (ноябрь 2005 г.). «Адаптивная экспоненциальная модель интеграции и активации как эффективное описание нейронной активности». Журнал нейрофизиологии . 94 (5): 3637– 42. doi :10.1152/jn.00686.2005. PMID 16014787.
- ^ ab Fourcaud-Trocmé N, Hansel D, van Vreeswijk C, Brunel N (декабрь 2003 г.). «Как механизмы генерации спайков определяют реакцию нейронов на флуктуирующие входные сигналы». The Journal of Neuroscience . 23 (37): 11628– 40. doi :10.1523/JNEUROSCI.23-37-11628.2003. PMC 6740955 . PMID 14684865.
- ^ Ostojic S, Brunel N, Hakim V (август 2009). «Как связность, фоновая активность и синаптические свойства формируют кросс-корреляцию между последовательностями спайков». The Journal of Neuroscience . 29 (33): 10234– 53. doi :10.1523/JNEUROSCI.1275-09.2009. PMC 6665800. PMID 19692598 .
- ^ Górski T, Depannemaecker D, Destexhe A (январь 2021 г.). «Адаптивная экспоненциальная модель интеграции и срабатывания на основе проводимости». Neural Computation . 33 (1): 41– 66. doi : 10.1162/neco_a_01342 . PMID 33253029.
- ^ "Нейрональная динамика - учебник по нейронауке Вульфрама Герстнера, Вернера М. Кистлера, Ричарда Науда и Лиама Панински". neuronaldynamics.epfl.ch . Получено 14.02.2024 .
- ^ Гангули, Читтотош; Безугам, Сай Сукрут; Абс, Элизабет; Пайванд, Мелика; Дей, Соунак; Сури, Манан (2024-02-01). "Адаптация частоты спайков: объединение нейронных моделей и нейроморфных приложений". Communications Engineering . 3 (1): 22. doi : 10.1038/s44172-024-00165-9 . ISSN 2731-3395. PMC 11053160 .
- ^ Беллек, Гийом Эммануэль Фернан; Салаж, Дарьян; Субрамони, Ананд; Легенштейн, Роберт; Маасс, Вольфганг (2018). «Долгая кратковременная память и обучение обучению в сетях импульсных нейронов». Достижения в области нейронных систем обработки информации . arXiv : 1803.09574 .
- ^ Шабан, Ахмед; Безугам, Сай Сукрут; Сури, Манан (2021-07-09). «Адаптивный пороговый нейрон для рекуррентных импульсных нейронных сетей с аппаратной реализацией наноустройства». Nature Communications . 12 (1): 4234. Bibcode :2021NatCo..12.4234S. doi :10.1038/s41467-021-24427-8. ISSN 2041-1723. PMC 8270926 . PMID 34244491.
- ^ Bezugam, Sai Sukruth; Shaban, Ahmed; Suri, Manan (2023-05-21). "Нейроморфные рекуррентные импульсные нейронные сети для классификации жестов ЭМГ и маломощная реализация на Loihi". 2023 IEEE Международный симпозиум по схемам и системам (ISCAS) . IEEE. стр. 1– 5. arXiv : 2206.02061 . doi : 10.1109/ISCAS46773.2023.10181510. ISBN 978-1-6654-5109-3. S2CID 260004324.
- ^ Кобаяси, Рёта; Цубо, Ясухиро; Шиномото, Сигеру (2009). «Созданная на заказ модель нейрона со спайками, оснащенная адаптивным порогом с несколькими временными масштабами». Frontiers in Computational Neuroscience . 3 : 9. doi : 10.3389/neuro.10.009.2009 . ISSN 1662-5188. PMC 2722979. PMID 19668702 .
- ^ Bryant HL, Segundo JP (сентябрь 1976 г.). «Инициация спайка трансмембранным током: анализ белого шума». Журнал физиологии . 260 (2): 279– 314. doi :10.1113/jphysiol.1976.sp011516. PMC 1309092. PMID 978519 .
- ^ Mainen ZF, Sejnowski TJ (июнь 1995). «Надежность синхронизации спайков в неокортикальных нейронах». Science . 268 (5216): 1503– 6. Bibcode :1995Sci...268.1503M. doi :10.1126/science.7770778. PMID 7770778.
- ^ Manwani A, Koch C (ноябрь 1999 г.). «Обнаружение и оценка сигналов в зашумленной кабельной структуре, I: источники нейронного шума». Neural Computation . 11 (8): 1797– 829. doi :10.1162/089976699300015972. PMID 10578033. S2CID 12298894. Архивировано из оригинала 2021-03-07 . Получено 2021-04-04 .
- ^ abcd Stein RB (март 1965). "Теоретический анализ нейронной изменчивости". Biophysical Journal . 5 (2): 173– 94. Bibcode :1965BpJ.....5..173S. doi :10.1016/s0006-3495(65)86709-1. PMC 1367716 . PMID 14268952.
- ^ abcdefghi Gerstner W, van Hemmen JL (январь 1992). «Ассоциативная память в сети „шипящих“ нейронов». Сеть: вычисления в нейронных системах . 3 (2): 139– 164. doi :10.1088/0954-898X_3_2_004. ISSN 0954-898X.
- ^ ab Дитлевсен С, Лански П (январь 2005 г.). «Оценка входных параметров в нейронной модели Орнштейна–Уленбека». Physical Review E. 71 ( 1 Pt 1): 011907. Bibcode : 2005PhRvE..71a1907D. doi : 10.1103/PhysRevE.71.011907. PMID 15697630.
- ^ Richardson MJ (август 2007 г.). "Ответ частоты импульсов линейных и нелинейных интегрирующих и импульсных нейронов на модулированный синаптический привод на основе тока и проводимости". Physical Review E. 76 ( 2 Pt 1): 021919. Bibcode : 2007PhRvE..76b1919R. doi : 10.1103/PhysRevE.76.021919. PMID 17930077.
- ^ Брунель Н. (2000-05-01). «Динамика редко связанных сетей возбуждающих и тормозных импульсных нейронов». Журнал вычислительной нейронауки . 8 (3): 183–208 . doi :10.1023/A:1008925309027. PMID 10809012. S2CID 1849650.
- ^ Йоханнесма ПИ (1968). «Модели диффузии для стохастической активности нейронов». В Caianelleo ER (ред.). Нейронные сети . Springer. стр. 116–144 . ISBN 9783642875960.
- ^ Gerstner W, van Hemmen JL (1992-01-01). «Ассоциативная память в сети „шипящих“ нейронов». Сеть: Вычисления в нейронных системах . 3 (2): 139– 164. doi :10.1088/0954-898X_3_2_004. ISSN 0954-898X.
- ^ Gerstner W (январь 1995). "Временная структура активности в моделях нейронных сетей" (PDF) . Physical Review E. 51 ( 1): 738– 758. Bibcode : 1995PhRvE..51..738G. doi : 10.1103/PhysRevE.51.738. PMID 9962697.
- ^ Truccolo W, Eden UT, Fellows MR, Donoghue JP, Brown EN (февраль 2005 г.). «Структура точечного процесса для соотнесения нейронной импульсной активности с историей импульсов, нейронным ансамблем и внешними ковариационными эффектами». Журнал нейрофизиологии . 93 (2): 1074– 89. doi :10.1152/jn.00697.2004. PMID 15356183.
- ^ abcd Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, Simoncelli EP (август 2008 г.). «Пространственно-временные корреляции и визуальная сигнализация в полной популяции нейронов». Nature . 454 (7207): 995– 9. Bibcode :2008Natur.454..995P. doi :10.1038/nature07140. PMC 2684455 . PMID 18650810.
- ^ Weiss TF (ноябрь 1966). «Модель периферической слуховой системы». Kybernetik . 3 (4): 153–75 . doi :10.1007/BF00290252. PMID 5982096. S2CID 30861035.
- ^ abcdefghi Gerstner W (январь 2000 г.). "Динамика популяции импульсных нейронов: быстрые переходы, асинхронные состояния и блокировка" (PDF) . Neural Computation . 12 (1): 43– 89. doi :10.1162/089976600300015899. PMID 10636933. S2CID 7832768.
- ^ Naud R, Gerstner W (2012-10-04). Sporns O (ред.). "Кодирование и декодирование с адаптирующимися нейронами: популяционный подход к гистограмме перистимульного времени". PLOS Computational Biology . 8 (10): e1002711. Bibcode : 2012PLSCB...8E2711N. doi : 10.1371/journal.pcbi.1002711 . PMC 3464223. PMID 23055914 .
- ^ Gerstner W, Ritz R, van Hemmen JL (октябрь 1993 г.). «Почему спайки? Хеббианское обучение и извлечение разрешенных во времени паттернов возбуждения». Biological Cybernetics . 69 ( 5– 6): 503– 15. doi :10.1007/BF00199450. PMID 7903867. S2CID 6195748.
- ^ ab Paninski L (ноябрь 2004 г.). "Оценка максимального правдоподобия каскадных точечных процессов нейронных моделей кодирования". Сеть: Вычисления в нейронных системах . 15 (4): 243– 62. doi : 10.1088/0954-898X_15_4_002 . PMID 15600233. S2CID 848548.
- ^ abcd Kistler WM, Gerstner W, Hemmen JL (1997-07-01). "Сведение уравнений Ходжкина-Хаксли к пороговой модели с одной переменной". Neural Computation . 9 (5): 1015– 1045. doi :10.1162/neco.1997.9.5.1015. ISSN 0899-7667. S2CID 9861477.
- ^ ab Gerstner W (январь 1995). «Временная структура активности в моделях нейронных сетей». Physical Review E. 51 ( 1): 738– 758. Bibcode :1995PhRvE..51..738G. doi :10.1103/PhysRevE.51.738. PMID 9962697.
- ^ Galves A, Löcherbach E (2013). «Бесконечные системы взаимодействующих цепей с памятью переменной длины — стохастическая модель для биологических нейронных сетей». Журнал статистической физики . 151 (5): 896–921 . arXiv : 1212.5505 . Bibcode : 2013JSP...151..896G. doi : 10.1007/s10955-013-0733-9. S2CID 119161279.
- ^ Фицхью Р. (июль 1961 г.). «Импульсы и физиологические состояния в теоретических моделях нервной мембраны». Biophysical Journal . 1 (6): 445–66 . Bibcode : 1961BpJ.....1..445F. doi : 10.1016/S0006-3495(61)86902-6. PMC 1366333. PMID 19431309 .
- ^ ФицХью Р., Ижикевич Э. (2006). "Модель ФицХью-Нагумо". Scholarpedia . 1 (9): 1349. Bibcode :2006SchpJ...1.1349I. doi : 10.4249/scholarpedia.1349 .
- ^ abcd Методы нейронного моделирования: от ионов к сетям (2-е изд.). [Место публикации не указано]: Mit Press. 2003. ISBN 0-262-51713-2. OCLC 947133821.
- ^ Rinzel J, Ermentrout B (август 1998). "Глава 7: Анализ нервной возбудимости и колебаний". В Segev I, Koch C (ред.). Методы нейронного моделирования . MIT Press. стр. 251. ISBN 978-0262517133.
- ^ ab Hindmarsh J, Cornelius P (2005-10-01). "Развитие модели хиндмарш-роуз для разрыва". Разрыв . WORLD SCIENTIFIC. стр. 3–18 . doi :10.1142/9789812703231_0001. ISBN 978-981-256-506-8.
- ^ ab Ermentrout G, Kopell N (1986). «Параболический всплеск в возбудимой системе, связанной с медленным колебанием». SIAM Journal on Applied Mathematics . 46 (2): 233– 253. doi :10.1137/0146017. ISSN 0036-1399.
- ^ ab Ermentrout B (июль 1996 г.). «Мембраны типа I, кривые сброса фазы и синхронность». Neural Computation . 8 (5): 979– 1001. doi :10.1162/neco.1996.8.5.979. PMID 8697231. S2CID 17168880.
- ^ ab Siebert WM (1970-05-01). "Частотная дискриминация в слуховой системе: механизмы места или периодичности?". Труды IEEE . 58 (5): 723– 730. doi :10.1109/PROC.1970.7727. ISSN 0018-9219.
- ^ ab Siebert WM (июнь 1965). «Некоторые следствия стохастического поведения первичных слуховых нейронов». Kybernetik . 2 (5): 206– 15. doi :10.1007/BF00306416. PMID 5839007. S2CID 9744183.
- ^ abcdefghij Носсенсон Н, Мессер Х (2010). "Моделирование паттерна срабатывания нейрона с использованием двухуровневой цепи Маркова". Семинар IEEE Sensor Array and Multichannel Signal Processing Workshop 2010. doi : 10.1109/SAM.2010.5606761. ISBN 978-1-4244-8978-7. S2CID 10973225.
- ^ abcdefg Носсенсон Н., Мессер Х. (апрель 2012 г.). «Оптимальное последовательное обнаружение стимулов из многоэлементных записей, полученных в густонаселенных регионах мозга». Neural Computation . 24 (4): 895–938 . doi :10.1162/NECO_a_00257. PMID 22168560. S2CID 16994688.
- ^ abcdefghijklmn Носсенсон Н, Магал Н, Мессер Х (2016). «Обнаружение стимулов от многонейронной активности: эмпирическое исследование и теоретические выводы». Neurocomputing . 174 : 822– 837. doi :10.1016/j.neucom.2015.10.007.
- ^ Berry MJ, Meister M (март 1998). «Рефрактерность и нейронная точность». Журнал нейронауки . 18 (6): 2200– 11. doi :10.1523/JNEUROSCI.18-06-02200.1998. PMC 6792934. PMID 9482804 .
- ^ ab Kass RE, Ventura V (август 2001 г.). «Модель вероятности спайк-поезда». Neural Computation . 13 (8): 1713– 20. doi :10.1162/08997660152469314. PMID 11506667. S2CID 9909632.
- ^ ab Gaumond RP, Molnar CE, Kim DO (сентябрь 1982 г.). «Зависимость вероятности разряда спайка кошачьего нервного волокна от стимула и восстановления». Журнал нейрофизиологии . 48 (3): 856–73 . doi :10.1152/jn.1982.48.3.856. PMID 6290620.
- ^ Миллер MI, Марк KE (июль 1992 г.). «Статистическое исследование паттернов разряда кохлеарного нерва в ответ на сложные речевые стимулы». Журнал акустического общества Америки . 92 (1): 202– 9. Bibcode : 1992ASAJ...92..202M. doi : 10.1121/1.404284. PMID 1324958.
- ^ ab Johnson DH, Swami A (август 1983). «Передача сигналов по образцам разряда волокон слухового нерва». Журнал акустического общества Америки . 74 (2): 493– 501. Bibcode : 1983ASAJ...74..493J. doi : 10.1121/1.389815. PMID 6311884.
- ^ Chichilnisky EJ (май 2001). "Простой анализ белого шума нейронных световых реакций". Network: Computation in Neural Systems . 12 (2): 199– 213. doi :10.1080/713663221. PMID 11405422.
- ^ abcde Nossenson N (2013). Model Based Detection of a Stimulus Presence from Neurophysiological Signals (PDF) (Ph.D. thesis). Библиотека точных наук и инженерии Неймана, Тель-Авивский университет: Университет Тель-Авива. Архивировано из оригинала (PDF) 2017-03-05 . Получено 2016-04-12 .
- ^ Koehler SD, Pradhan S, Manis PB, Shore SE (февраль 2011 г.). «Соматосенсорные входы изменяют время слуховых спайков в главных клетках дорсального кохлеарного ядра». The European Journal of Neuroscience . 33 (3): 409– 20. doi :10.1111/j.1460-9568.2010.07547.x. PMC 3059071 . PMID 21198989.
- ^ Reches A, Gutfreund Y (февраль 2008 г.). «Стимул-специфические адаптации в системе управления взглядом у сипухи». The Journal of Neuroscience . 28 (6): 1523– 33. doi :10.1523/JNEUROSCI.3785-07.2008. PMC 6671572. PMID 18256273 .
- ^ Ван X, Лу Т, Снайдер РК, Лян Л (май 2005). «Устойчивая активация слуховой коры, вызванная предпочтительными стимулами». Nature . 435 (7040): 341– 6. Bibcode :2005Natur.435..341W. doi :10.1038/nature03565. PMID 15902257. S2CID 4312195.
- ^ Taberner AM, Liberman MC (январь 2005 г.). «Свойства ответа отдельных волокон слухового нерва у мыши». Журнал нейрофизиологии . 93 (1): 557– 69. doi :10.1152/jn.00574.2004. PMID 15456804.
- ^ Хенневин Э., Харс Б., Махо К., Блох В. (1995-07-01). «Обработка усвоенной информации в парадоксальном сне: значимость для памяти». Поведенческие исследования мозга . Функция сна. 69 ( 1– 2): 125– 35. doi :10.1016/0166-4328(95)00013-J. PMID 7546303. S2CID 4034082.
- ^ Rodieck RW (декабрь 1965 г.). «Количественный анализ реакции ганглиозных клеток сетчатки кошки на зрительные стимулы». Vision Research . 5 (11): 583– 601. doi :10.1016/0042-6989(65)90033-7. PMID 5862581.
- ^ ab Enroth-Cugell C, Lennie P (июнь 1975). «Контроль разряда ганглиозных клеток сетчатки с помощью рецептивного поля окружения». Журнал физиологии . 247 (3): 551–78 . doi :10.1113/jphysiol.1975.sp010947. PMC 1309488. PMID 1142301 .
- ^ Enroth-Cugell C, Shapley RM (сентябрь 1973 г.). «Адаптация и динамика ганглиозных клеток сетчатки кошки». Журнал физиологии . 233 (2): 271– 309. doi :10.1113/jphysiol.1973.sp010308. PMC 1350567. PMID 4747229 .
- ^ Sagdullaev BT, McCall MA (2005-09-01). «Размер и интенсивность стимула изменяют фундаментальные свойства рецептивного поля ганглиозных клеток сетчатки мыши in vivo». Visual Neuroscience . 22 (5): 649–59 . doi :10.1017/S0952523805225142. PMID 16332276. S2CID 7699161.
- ^ Nagel KI, Wilson RI (февраль 2011 г.). «Биофизические механизмы, лежащие в основе динамики нейронов обонятельных рецепторов». Nature Neuroscience . 14 (2): 208– 16. doi :10.1038/nn.2725. PMC 3030680 . PMID 21217763.
- ^ Tommerdahl M, Delemos KA, Whitsel BL, Favorov OV, Metz CB (июль 1999). «Реакция передней теменной коры на кожный флаттер против вибрации». Журнал нейрофизиологии . 82 (1): 16– 33. doi :10.1152/jn.1999.82.1.16. PMID 10400931. S2CID 14729461.
- ^ Хадипур Никтараш А, Шахиди ГА (2004-03-01). "Влияние активности внутренней петли бледный шар-педункулопонтийный мост на передачу колебательной активности субталамического ядра-внешнего бледного шара-пейсмекера в кору". Журнал вычислительной нейронауки . 16 (2): 113–27 . doi :10.1023/B:JCNS.0000014105.87625.5f. PMID 14758061. S2CID 20728260.
- ^ Yamanaka Y, Kitamura N, Shinohara H, Takahashi K, Shibuya I (январь 2013 г.). «Глутамат вызывает срабатывание посредством активации каинатных рецепторов в нейронах добавочных долей курицы». Журнал сравнительной физиологии A: Neuroethology, Sensory, Neural & Behavioral Physiology . 199 (1): 35– 43. doi :10.1007/s00359-012-0766-6. PMID 23064516. S2CID 15527085.
- ^ Мюллер М., Робертсон Д., Йейтс Г.К. (сентябрь 1991 г.). «Функции скорости и уровня первичных слуховых нервных волокон: доказательства квадратичного поведения всех категорий волокон у морской свинки». Hearing Research . 55 (1): 50– 6. doi :10.1016/0378-5955(91)90091-M. PMID 1752794. S2CID 40343090.
- ^ Джонсон ДХ, Кианг, Нью-Йорк (июль 1976 г.). «Анализ разрядов, зарегистрированных одновременно из пар волокон слухового нерва». Biophysical Journal . 16 (7): 719– 34. Bibcode : 1976BpJ....16..719J. doi : 10.1016/s0006-3495(76)85724-4. PMC 1334896. PMID 938715 .
- ^ Bullock TH (1997-01-01). «Сравнительная физиология акустических и смежных центральных анализаторов». Acta Oto-Laryngologica. Supplementum . 532 (sup532): 13– 21. doi :10.3109/00016489709126139. PMID 9442839.
- ^ Holstein SB, Buchwald JS, Schwafel JA (ноябрь 1969). «Прогрессивные изменения в моделях слухового ответа на повторяющийся тон во время нормального бодрствования и паралича». Brain Research . 16 (1): 133– 48. doi :10.1016/0006-8993(69)90090-0. PMID 5348845.
- ^ Rizzo JF (июнь 2011 г.). «Обновление исследований в области протезирования сетчатки: проект по имплантации сетчатки в Бостоне». Журнал нейроофтальмологии . 31 (2): 160– 8. doi : 10.1097/wno.0b013e31821eb79e. PMID 21593628. S2CID 17213342.
- ^ Peterman MC, Mehenti NZ, Bilbao KV, Lee CJ, Leng T, Noolandi J и др. (ноябрь 2003 г.). «Искусственный синаптический чип: гибкий ретинальный интерфейс на основе направленного роста ретинальных клеток и стимуляции нейротрансмиттеров». Искусственные органы . 27 (11): 975–85 . doi :10.1046/j.1525-1594.2003.07307.x. PMID 14616516.
- ^ Iezzi R, Finlayson P, Xu Y, Katragadda R (6–9 сентября 2009 г.). Микрофлюидные нейротрансмиттерные нейронные интерфейсы для ретинального протезирования . Ежегодная международная конференция IEEE Engineering in Medicine and Biology Society 2009 г. Миннеаполис: IEEE Engineering in Medicine and Biology Society. стр. 4563–5 . doi :10.1109/IEMBS.2009.5332694. ISBN 978-1-4244-3296-7. PMID 19963838. S2CID 2751102.
- ^ Yoshida K, Farina D, Akay M, Jensen W (2010-03-01). «Многоканальные интраневральные и внутримышечные методы для многоблочной записи и использования в активных протезах». Труды IEEE . 98 (3): 432– 449. doi :10.1109/JPROC.2009.2038613. ISSN 0018-9219. S2CID 23631268.
- ^ Bruns TM, Wagenaar JB, Bauman MJ, Gaunt RA, Weber DJ (апрель 2013 г.). «Управление функциональной электрической стимуляцией задних конечностей в реальном времени с использованием обратной связи от записей ганглиев задних корешков». Journal of Neural Engineering . 10 (2): 026020. Bibcode :2013JNEng..10b6020B. doi :10.1088/1741-2560/10/2/026020. PMC 3640462 . PMID 23503062.
- ^ "BrainGate - Главная". braingate2.org . 2015-12-04 . Получено 2016-04-06 .
- ^ ab Hay E, Hill S, Schürmann F, Markram H, Segev I (июль 2011 г.). "Модели пирамидальных клеток неокортексного слоя 5b, захватывающих широкий спектр дендритных и перисоматических активных свойств". PLOS Computational Biology . 7 (7): e1002107. Bibcode :2011PLSCB...7E2107H. doi : 10.1371/journal.pcbi.1002107 . PMC 3145650 . PMID 21829333.
- ^ Markram H, Muller E, Ramaswamy S, Reimann MW, Abdellah M, Sanchez CA и др. (октябрь 2015 г.). «Реконструкция и моделирование неокортикальной микросхемы». Cell . 163 (2): 456–92 . doi : 10.1016/j.cell.2015.09.029 . PMID 26451489. S2CID 14466831.
- ^ Forrest MD (апрель 2015 г.). «Моделирование действия алкоголя на детальную модель нейрона Пуркинье и более простую суррогатную модель, которая работает >400 раз быстрее». BMC Neuroscience . 16 (27): 27. doi : 10.1186/s12868-015-0162-6 . PMC 4417229 . PMID 25928094.
- ^ Sardi S, Vardi R, Sheinin A, Goldental A, Kanter I (декабрь 2017 г.). «Новые типы экспериментов показывают, что нейрон функционирует как несколько независимых пороговых единиц». Scientific Reports . 7 (1): 18036. Bibcode :2017NatSR...718036S. doi :10.1038/s41598-017-18363-1. PMC 5740076 . PMID 29269849.









![{\displaystyle f(I)={\begin{cases}0,&I\leq I_{\mathrm {th} }\\\left[t_{\mathrm {ref} }-R_{\mathrm {m} }C_{\mathrm {m} }\log \left(1-{\tfrac {V_{\mathrm {th} }}{IR_{\mathrm {m} }}}\right)\right]^{-1},&I>I_{\mathrm {th} }\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d2b9ee97278ff7f139dc76afecd9d3336a35a5b)
![{\displaystyle \tau _{\mathrm {m} }{\frac {dV_{\mathrm {m} }(t)}{dt}}=RI(t)-[V_{\mathrm {m} }(t)-E_{\mathrm {m} }]-R\sum _{k}w_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8345759b126e0ae20788d2be0b5f74b89dd598)
![{\displaystyle \tau _ {k}{\frac {dw_ {k}(t)}{dt}} = -a_ {k}[V_ {\ mathrm {m} } (t) -E_ {\ mathrm {m} }] -w_ {k} + b_ {k} \ tau _ {k} \ sum _ {f} \ delta (tt^ {f})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8561a663fc284164af5004d49dda606de65f3153)



![{\displaystyle {\frac {dV}{dt}}-{\frac {R}{\tau _{m}}}I(t)={\frac {1}{\tau _{m}}}\left[E_{m}-V+\Delta _{T}\exp \left({\frac {V-V_{T}}{\Delta _{T}}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2681d0764425e62cdbe8563763546145ac871888)




![{\displaystyle \tau _{m}{\frac {dV}{dt}}=RI(t)+\left[E_{m}-V+\Delta _{T}\exp \left({\frac {V-V_{T}}{\Delta _{T}}}\right)\right]-Rw}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc57795f1765df722678bfca445163588b4898aa)
![{\displaystyle \tau {\frac {dw(t)}{dt}}=-a[V_{\mathrm {m} }(t)-E_{\mathrm {m} }]-w+b\tau \delta (tt^{f})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad1061c0bd8fa3f0894982dfd5913c5114471f9)





![{\displaystyle v_{th}(t)=v_{th0}+{\frac {\sum \theta (t-t_{f})}{f}}=v_{th0}+{\frac {\sum \theta _{0}\exp \left[-{\frac {(t-t_{f})}{\tau _{\theta }}}\right]}{f}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3092291632a18a195d5cb17f97c121cac909b46b)
![{\displaystyle \theta (t)=\theta _{0}\exp \left[-{\frac {t}{\tau _{\theta }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dcd1b31f7ffad6905bffe2135e8160cbab229a5)








![{\displaystyle p_{j1}=\exp \left[-{\frac {\delta t}{\tau _{b1}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5417632ba41e7bf5dd3f3698b17d3f4ca39c7d6e)
![{\displaystyle p_{j2}=\exp \left[-{\frac {\delta t}{\tau _{b2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1f4efbe00768358ce5e4ba3143407cbf3594a5)




![{\displaystyle \tau _{m}{\frac {dV}{dt}}=[E_{m}-V]+RI(t)+R\xi (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2471c95b51d6f1a179aaeacc81d4680cbc66d53f)
![{\displaystyle dV=[E_{m}-V+RI(t)]{\frac {dt}{\tau _{m}}}+\sigma \,dW}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c77157af02d1ea4ea0e312efa41ed7083ff17525)

![{\displaystyle \Delta V=[E_{m}-V+RI(t)]{\frac {\Delta t}{\tau _{m}}}+\sigma {\sqrt {\tau _{m}}}y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac593d7a28da8c87a36c135c66923293472f26df)






![{\displaystyle f(VV_{th})={\frac {1}{\tau _{0}}}\exp[\beta (VV_{th})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0e6a01b14e279fb530c4c37647a0f4dcf60b1b1)




![{\displaystyle P_{F}(t_{n})=F[V(t_{n})-V_{th}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ef050261c3ab3b90026f75a47810dc554c3fbec)

![{\displaystyle F(x)=0,5[1+\tanh(\gamma x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506d2b8f3cb095fc95e2993bea559a297013a5ed)

![{\displaystyle F(y_{n})\approx 1-\exp[y_{n}\Delta t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cafeec2276d1633d2d283c3ba07623c0b3f206d5)





![{\displaystyle f(V-\vartheta (t))={\frac {1}{\tau _{0}}}\exp[\beta (V-\vartheta (t))]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b0258498f0e91cf25539b60de5af5a5b24dcfcb)


















![{\displaystyle f(V-\vartheta)={\frac {1}{\tau _{0}}}\exp[\beta (VV_{th})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bd95a6edcc2e90476af83affbc51d150042d33b)















![{\displaystyle {\frac {d\theta (t)}{dt}}=(I-I_{0})[1+\cos(\theta )]+[1-\cos(\theta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecbba69c0c299fc9ba2a49a79be5d607200af4c3)
![{\displaystyle \tau _{\mathrm {m} }{\frac {dV_{\mathrm {m} }(t)}{dt}}=(I-I_{0})R+[V_{\mathrm {m} }(t)-E_{\mathrm {m} }][V_{\mathrm {m} }(t)-V_{\mathrm {T} }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8392a8de9357950491d89517ec59294d6ef35e5)
![{\displaystyle [t,t+\Delta _{t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a5f74c8e9f1b771d10e66322f05d9692676551b)
![{\displaystyle g[s(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f02d6c931d32be9a417598bb7164a38b18e7c7)

![{\displaystyle P_{\text{spike}}(t\in [t',t'+\Delta _{t}])=\Delta _{t}\cdot g[s(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c518881857d805263d6674a39ae79d3b830a06c)
![{\displaystyle g[s(t)]\propto s^{2}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/279ad33854b65b37667308913d562014bdb7f30a)


![{\displaystyle R_{\text{огонь}}(t)={\frac {P_{\text{шип}}(t;\Delta _{t})}{\Delta _{t}}}=[y(t)+R_{0}]\cdot P_{0}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1038693094674ba67b2e424be6eae51db081721e)
![{\displaystyle {\dot {P}}_{0}=-[y(t)+R_{0}+R_{1}]\cdot P_{0}(t)+R_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/830fe4d93362af37a7b4d97c1902b7db1826f9e1)


![{\ displaystyle I _ {\ mathrm {AMPA} } (t, V) = {\ bar {g}} _ {\ mathrm {AMPA} } \ cdot [O] \ cdot (V (t) -E _ {\ mathrm {AMPA} })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a00bcdac49e857cbf0e2440b47d7760a17d7bdc5)
![{\displaystyle I_{\mathrm {NMDA} }(t,V)={\bar {g}}_{\mathrm {NMDA} }\cdot B(V)\cdot [O]\cdot (V(t)-E_{\mathrm {NMDA} })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d0bedfd5fbcaada1bfb385795d52950e6429e10)
![{\ displaystyle I _ {\ mathrm {GABA_ {A}} } (t, V) = {\ bar {g}} _ {\ mathrm {GABA_ {A}} } \ cdot ([O_ {1}] + [O_ {2}]) \ cdot (V (t) -E _ {\ mathrm {Cl} })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0a4898469d8c0f8a2a1b4fd1620c3f69795f85b)
![{\displaystyle I_ {\ mathrm {GABA_ {B}} } (t, V) = {\ bar {g}} _ {\ mathrm {GABA_ {B}} } \ cdot {\ tfrac {[G] ^ {n}} {[G] ^ {n} + K _ {\ mathrm {d} }}} \ cdot (V (t) -E _ {\ mathrm {K} })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09fdce1c61e28bac586e48a928523772a0f4187f)

















