IEEE 754
| Форматы с плавающей точкой |
|---|
| IEEE 754 |
|
| Другой |
| Альтернативы |
Стандарт IEEE для арифметики с плавающей точкой ( IEEE 754 ) — это технический стандарт для арифметики с плавающей точкой, первоначально установленный в 1985 году Институтом инженеров по электротехнике и электронике (IEEE). Стандарт решает множество проблем, обнаруженных в различных реализациях с плавающей точкой, которые затрудняют их надежное и переносимое использование . Многие аппаратные устройства с плавающей точкой используют стандарт IEEE 754.
Стандарт определяет:
- арифметические форматы: наборы двоичных и десятичных данных с плавающей точкой, которые состоят из конечных чисел (включая нули со знаком и субнормальные числа ), бесконечностей и специальных значений «не число» ( NaN ).
- форматы обмена: кодировки (битовые строки), которые могут использоваться для обмена данными с плавающей точкой в эффективной и компактной форме
- правила округления: свойства, которые должны соблюдаться при округлении чисел во время арифметических действий и преобразований
- операции: арифметические и другие операции (например, тригонометрические функции ) в арифметических форматах
- обработка исключений: индикация исключительных ситуаций (таких как деление на ноль , переполнение и т. д.)
IEEE 754-2008 , опубликованный в августе 2008 года, включает в себя почти весь исходный стандарт IEEE 754-1985 , а также стандарт IEEE 854-1987 для арифметики чисел с плавающей точкой, независимой от основания системы счисления . Текущая версия, IEEE 754-2019, была опубликована в июле 2019 года. [1] Это незначительная переработка предыдущей версии, включающая в себя в основном пояснения, исправления дефектов и новые рекомендуемые операции.
История
Необходимость в стандарте с плавающей точкой возникла из-за хаоса в деловой и научной вычислительной индустрии в 1960-х и 1970-х годах. IBM использовала шестнадцатеричный формат с плавающей точкой с более длинной мантиссой и более короткой экспонентой [ требуется разъяснение ] . Компьютеры CDC и Cray использовали представление с дополнением по единицам , которое допускало значения +0 и −0. 60-битные компьютеры CDC не имели полных 60-битных сумматоров, поэтому целочисленная арифметика была ограничена 48 битами точности от блока с плавающей точкой. Обработка исключений из-за деления на ноль была разной на разных компьютерах. Перемещение данных между системами и даже повторение одних и тех же вычислений на разных системах часто было затруднительным.
Первый стандарт IEEE для арифметики с плавающей точкой, IEEE 754-1985 , был опубликован в 1985 году. Он охватывал только двоичную арифметику с плавающей точкой.
Новая версия IEEE 754-2008 была опубликована в августе 2008 года после семилетнего процесса пересмотра под председательством Дэна Зураса и редактором Майком Коулишоу . Она заменила как IEEE 754-1985 (двоичная арифметика с плавающей точкой), так и IEEE 854-1987 Standard for Radix-Independent Floating-Point Arithmetic . Двоичные форматы исходного стандарта включены в этот новый стандарт вместе с тремя новыми базовыми форматами, одним двоичным и двумя десятичными. Чтобы соответствовать текущему стандарту, реализация должна реализовать по крайней мере один из базовых форматов как арифметический формат и формат обмена.
Международный стандарт ISO/IEC/IEEE 60559:2011 (с содержанием, идентичным IEEE 754-2008) был одобрен для принятия через ISO / IEC JTC 1 /SC 25 в соответствии с Соглашением ISO/IEEE PSDO [2] [3] и опубликован. [4]
Текущая версия IEEE 754-2019, опубликованная в июле 2019 года, получена из IEEE 754-2008 и заменяет его после процесса пересмотра, начатого в сентябре 2015 года под председательством Дэвида Г. Хафа и под редакцией Майка Коулишоу. Она включает в себя в основном разъяснения (например, totalOrder ) и исправления дефектов (например, minNum ), но также включает некоторые новые рекомендуемые операции (например, augmentedAddition ). [5] [6]
Международный стандарт ISO/IEC 60559:2020 (с содержанием, идентичным IEEE 754-2019) был одобрен для принятия через ISO/IEC JTC 1 /SC 25 и опубликован. [7]
Следующая предполагаемая редакция стандарта состоится в 2029 году. [8]
Форматы
Формат IEEE 754 — это «набор представлений числовых значений и символов». Формат может также включать способ кодирования набора. [9]
Формат с плавающей точкой определяется как
- основание (также называемое основанием ) b , которое в IEEE 754 равно 2 (двоичное) или 10 (десятичное);
- точность p ;
- диапазон показателей от emin до emax , где emin = 1 − emax или, что эквивалентно, emin = − ( emax − 1) для всех форматов IEEE 754.
Формат включает в себя
- Конечные числа, которые можно описать тремя целыми числами: s = знак (ноль или единица), c = мантисса (или коэффициент ), имеющая не более p цифр при записи в основании b (т. е. целое число в диапазоне от 0 до b p − 1), и q = показатель степени , такой что emin ≤ q + p − 1 ≤ emax . Числовое значение такого конечного числа равно (−1) s × c × b q . [a] Более того, существуют два нулевых значения, называемые знаковыми нулями : бит знака определяет, является ли ноль +0 (положительным нулем) или −0 (отрицательным нулем).
- Две бесконечности: +∞ и −∞.
- Два вида NaN (не-числа): тихий NaN (qNaN) и сигнальный NaN (sNaN).
Например, если b = 10, p = 7 и emax = 96, то emin = −95, мантисса удовлетворяет условию 0 ≤ c ≤9 999 999 , а показатель степени удовлетворяет −101 ≤ q ≤ 90 . Следовательно, наименьшее ненулевое положительное число, которое может быть представлено, равно 1 × 10 −101 , а наибольшее равно 9999999 × 10 90 (9,999999 × 10 96 ), поэтому полный диапазон чисел равен −9,999999 × 10 96 до 9,999999 × 10 96 . Числа − b 1− emax и b 1− emax (здесь −1×10 −95 и 1×10 −95 ) являются наименьшими (по величине) нормальными числами ; ненулевые числа между этими наименьшими числами называются субнормальными числами .
Представление и кодирование в памяти
Некоторые числа могут иметь несколько возможных представлений с плавающей точкой. Например, если b = 10 и p = 7, то −12,345 может быть представлено как −12345×10 −3 , −123450×10 −4 и −1234500×10 −5 . Однако для большинства операций, таких как арифметические операции, результат (значение) не зависит от представления входных данных.
Для десятичных форматов допустимо любое представление, а набор этих представлений называется когортой . Когда результат может иметь несколько представлений, стандарт определяет, какой член когорты выбирается.
Для двоичных форматов представление делается уникальным путем выбора наименьшего представимого показателя, позволяющего точно представить значение. Кроме того, показатель не представляется напрямую, а добавляется смещение , так что наименьший представимый показатель представляется как 1, а 0 используется для субнормальных чисел. Для чисел с показателем в нормальном диапазоне (поле показателя не является ни одним из единиц, ни одним из нулей) ведущий бит мантиссы всегда будет равен 1. Следовательно, ведущий 1 может подразумеваться, а не явно присутствовать в кодировке памяти, и в соответствии со стандартом явно представленная часть мантиссы будет находиться между 0 и 1. Это правило называется соглашением о ведущих битах , неявным соглашением о битах или соглашением о скрытых битах . Это правило позволяет двоичному формату иметь дополнительный бит точности. Соглашение о ведущих битах не может использоваться для субнормальных чисел, поскольку у них показатель вне нормального диапазона показателя и масштабируется по наименьшему представленному показателю, как это используется для наименьших нормальных чисел.
Из-за возможности множественного кодирования (по крайней мере, в форматах, называемых форматами обмена ), NaN может нести другую информацию: знаковый бит (который не имеет значения, но может использоваться некоторыми операциями) и полезную нагрузку , которая предназначена для диагностической информации, указывающей на источник NaN (но полезная нагрузка может иметь и другие применения, такие как NaN-boxing [10] [11] [12] ).
Базовые и обменные форматы
Стандарт определяет пять основных форматов, названных по их числовой базе и количеству бит, используемых в их кодировке обмена. Существует три основных формата двоичных чисел с плавающей точкой (кодируемых 32, 64 или 128 битами) и два основных формата десятичных чисел с плавающей точкой (кодируемых 64 или 128 битами). Форматы binary32 и binary64 являются одинарным и двойным форматами IEEE 754-1985 соответственно. Соответствующая реализация должна полностью реализовывать по крайней мере один из основных форматов.
Стандарт также определяет форматы обмена , которые обобщают эти базовые форматы. [13] Для двоичных форматов требуется соглашение о ведущих битах. В следующей таблице обобщены некоторые возможные форматы обмена (включая базовые форматы).
| Значимая часть | Экспонента | Свойства [б] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | Общее название | Радикс | Цифры [c] | Десятичные цифры [d] | Мин. | Макс | МАКСВАЛ | log 10 МАКСЗНАЧ | MINVAL >0 (нормально) | MINVAL >0 (субнорма) | Примечания |
| двоичный16 | Половинная точность | 2 | 11 | 3.31 | −14 | 15 | 65504 | 4.816 | 6.10·10 −5 | 5,96·10 −8 | Обмен |
| двоичный32 | Одинарная точность | 2 | 24 | 7.22 | −126 | +127 | 3,40·10 38 | 38.532 | 1,18·10 −38 | 1,40·10 −45 | Базовый |
| двоичный64 | Двойная точность | 2 | 53 | 15.95 | −1022 | +1023 | 1,80·10 308 | 308.255 | 2,23·10 −308 | 4,94·10 −324 | Базовый |
| двоичный128 | Учетверённая точность | 2 | 113 | 34.02 | −16382 | +16383 | 1.19·10 4932 | 4932.075 | 3,36·10 −4932 | 6,48·10 −4966 | Базовый |
| двоичный256 | Восьмикратная точность | 2 | 237 | 71.34 | −262142 | +262143 | 1,61·10 78913 | 78913.207 | 2,48·10 −78913 | 2,25·10 −78984 | Обмен |
| decimal32 | 10 | 7 | 7 | −95 | +96 | 1,0·10 97 | 97 − 4,34·10 −8 | 1·10 −95 | 1·10 −101 | Обмен | |
| decimal64 | 10 | 16 | 16 | −383 | +384 | 1,0·10 385 | 385 − 4,34·10 −17 | 1·10 −383 | 1·10 −398 | Базовый | |
| десятичная128 | 10 | 34 | 34 | −6143 | +6144 | 1.0·10 6145 | 6145 − 4,34·10 −35 | 1·10 −6143 | 1·10 −6176 | Базовый | |
В таблице выше целые значения являются точными, тогда как значения в десятичной системе счисления (например, 1,0) являются округленными значениями. Минимальные показатели степени указаны для обычных чисел; специальное представление субнормальных чисел позволяет представлять даже меньшие (по величине) числа с некоторой потерей точности. Например, наименьшее положительное число, которое может быть представлено в двоичной системе счисления64, равно 2 −1074 ; вклад в число −1074 включает значение emin −1022 и все, кроме одного, из 53 значимых битов (2 −1022 − (53 − 1) = 2 −1074 ).
Десятичные цифры — это точность формата, выраженная в эквивалентном количестве десятичных цифр. Она вычисляется как цифры × логарифм 10 по основанию . Например, binary128 имеет примерно такую же точность, как и 34-значное десятичное число.
log 10 MAXVAL — это мера диапазона кодирования. Его целая часть — это наибольшая экспонента, показанная на выходе значения в научной нотации с одной ведущей цифрой в значащей части перед десятичной точкой (например, 1,698·10 38 — это близкое к наибольшему значение в binary32, 9,999999·10 96 — это наибольшее значение в decimal32).
Форматы binary32 (single) и binary64 (double) являются двумя наиболее распространенными форматами, используемыми сегодня. На рисунке ниже показана абсолютная точность для обоих форматов в диапазоне значений. Этот рисунок можно использовать для выбора подходящего формата с учетом ожидаемого значения числа и требуемой точности.
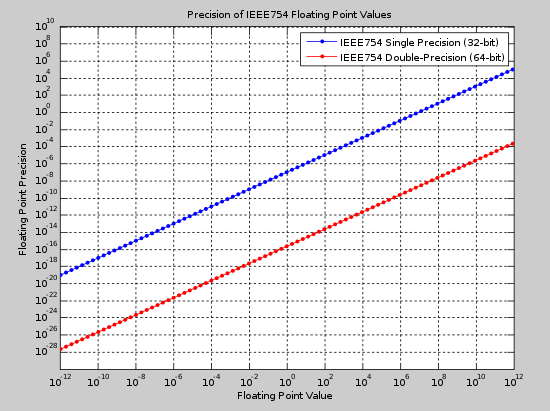
Пример макета для 32-битных чисел с плавающей точкой :

и 64-битная компоновка аналогична.
Расширенные и расширяемые форматы точности
Стандарт определяет необязательные расширенные и расширяемые форматы точности, которые обеспечивают большую точность, чем базовые форматы. [14] Расширенный формат точности расширяет базовый формат, используя большую точность и больший диапазон экспоненты. Расширяемый формат точности позволяет пользователю указывать точность и диапазон экспоненты. Реализация может использовать любое внутреннее представление, которое она выбирает для таких форматов; все, что нужно определить, это ее параметры ( b , p , и emax ). Эти параметры однозначно описывают набор конечных чисел (комбинации знака, мантиссы и экспоненты для заданного основания), которые она может представлять.
Стандарт рекомендует, чтобы стандарты языка предоставляли метод указания p и emax для каждого поддерживаемого основания b . [15] Стандарт рекомендует, чтобы стандарты языка и реализации поддерживали расширенный формат, который имеет большую точность, чем самый большой базовый формат, поддерживаемый для каждого основания b . [16] Для расширенного формата с точностью между двумя базовыми форматами диапазон экспоненты должен быть таким же большим, как и у следующего более широкого базового формата. Так, например, 64-битное двоичное число с расширенной точностью должно иметь 'emax' не менее 16383. 80-битный расширенный формат x87 соответствует этому требованию.
В оригинальном стандарте IEEE 754-1985 также была концепция расширенных форматов , но без обязательной связи между emin и emax . Например, 80-битный формат Motorola 68881 , [17] где emin = − emax , был соответствующим расширенным форматом, но стал несоответствующим в редакции 2008 года.
Форматы обмена
Форматы обмена предназначены для обмена данными с плавающей точкой с использованием битовой строки фиксированной длины для данного формата.
Двоичный
Для обмена двоичными числами с плавающей точкой определены форматы обмена длиной 16 бит, 32 бита, 64 бита и любые кратные 32 битам ≥ 128 [e] . 16-битный формат предназначен для обмена или хранения небольших чисел (например, для графики).
Схема кодирования для этих форматов двоичного обмена такая же, как и в IEEE 754-1985: бит знака, за которым следуют w битов экспоненты, которые описывают смещение экспоненты на смещение , и p − 1 битов, которые описывают мантисса. Ширина поля экспоненты для k -битного формата вычисляется как w = round(4 log 2 ( k )) − 13. Существующие 64- и 128-битные форматы следуют этому правилу, но 16- и 32-битные форматы имеют больше битов экспоненты (5 и 8 соответственно), чем эта формула могла бы предоставить (3 и 7 соответственно).
Как и в IEEE 754-1985, поле смещенной экспоненты заполнено всеми битами 1, чтобы указать либо бесконечность (поле конечной мантиссы = 0), либо NaN (поле конечной мантиссы ≠ 0). Для NaN, тихие NaN и сигнальные NaN различаются использованием самого старшего бита поля конечной мантиссы, [f] , а полезная нагрузка переносится в оставшихся битах.
Десятичная дробь
Для обмена десятичными числами с плавающей точкой определены форматы обмена любого кратного 32 битам. Как и в случае с двоичным обменом, схема кодирования для десятичных форматов обмена кодирует знак, экспоненту и мантиссу. Определены две различные кодировки на уровне битов, и обмен усложняется тем, что может потребоваться некоторый внешний индикатор используемой кодировки.
Два варианта позволяют кодировать мантисса как сжатую последовательность десятичных цифр с использованием плотно упакованной десятичной системы счисления или, в качестве альтернативы, как двоичное целое число . Первый вариант более удобен для прямой аппаратной реализации стандарта, тогда как второй больше подходит для программной эмуляции на двоичном компьютере. В любом случае набор чисел (комбинаций знака, мантиссы и экспоненты), которые могут быть закодированы, идентичен, а специальные значения (±ноль с минимальной экспонентой, ±бесконечность, тихие NaN и сигнальные NaN) имеют идентичные кодировки.
Правила округления
Стандарт определяет пять правил округления. Первые два правила округляют до ближайшего значения; остальные называются направленными округлениями :
Округление до ближайшего
- Округление до ближайшего, четное – округление до ближайшего значения; если число попадает посередине, оно округляется до ближайшего значения с четной наименее значащей цифрой.
- Округление до ближайшего, отклонение от нуля (или отклонение от нуля ) – округление до ближайшего значения; если число попадает на середину, оно округляется до ближайшего значения больше (для положительных чисел) или меньше (для отрицательных чисел).
В крайних случаях значение с величиной строго меньше будет округляться до минимального или максимального конечного числа (в зависимости от знака значения). Любые числа с точно такой величиной считаются связями; этот выбор связи может быть концептуализирован как середина между и , которые, если бы показатель степени не был ограничен, были бы следующими представимыми числами с плавающей точкой, большими по величине. Числа с величиной строго больше k округляются до соответствующей бесконечности. [18]
"Округлить до ближайшего, привязать к четному" — это значение по умолчанию для двоичных чисел с плавающей точкой и рекомендуемое значение по умолчанию для десятичных чисел. "Округлить до ближайшего, привязать к четному" требуется только для реализаций десятичных чисел. [19]
Направленные закругления
- Округление к 0 – направленное округление к нулю (также известное как усечение ).
- Округление в сторону +∞ – направленное округление в сторону положительной бесконечности (также известное как округление вверх или к потолку ).
- Округление в сторону −∞ – направленное округление в сторону отрицательной бесконечности (также известное как округление вниз или округление вниз ).
| Режим | Пример значения | |||
|---|---|---|---|---|
| +11.5 | +12.5 | −11,5 | −12,5 | |
| к ближайшему, связи с четным | +12.0 | +12.0 | −12.0 | −12.0 |
| к ближайшему, отстает от нуля | +12.0 | +13.0 | −12.0 | −13,0 |
| к 0 | +11.0 | +12.0 | −11.0 | −12.0 |
| к +∞ | +12.0 | +13.0 | −11.0 | −12.0 |
| к −∞ | +11.0 | +12.0 | −12.0 | −13,0 |
Если не указано иное, результат операции с плавающей точкой определяется путем применения функции округления к бесконечно точному (математическому) результату. Такая операция называется правильно округленной . Это требование называется правильным округлением . [20]
Требуемые операции
Необходимые операции для поддерживаемого арифметического формата (включая основные форматы) включают:
- Преобразования в целые числа и из них [21] [22]
- Предыдущие и последующие последовательные значения [21]
- Арифметические операции (сложение, вычитание, умножение, деление, квадратный корень, объединенное умножение-сложение , остаток, минимум, максимум) [21] [22]
- Преобразования (между форматами, в строки и из строк и т. д.) [23] [24]
- Масштабирование и (для десятичных чисел) квантование [25] [26]
- Копирование и манипулирование знаком (abs, negate и т.д.) [27]
- Сравнения и общее упорядочение [28] [29]
- Классификация чисел (субнормальные, конечные и т.д.) и проверка на NaN [30]
- Тестирование и установка флагов состояния [31]
Предикаты сравнения
Стандарт предоставляет предикаты сравнения для сравнения одного числа с плавающей точкой с другим в поддерживаемом арифметическом формате. [32] Любое сравнение с NaN рассматривается как неупорядоченное. −0 и +0 сравниваются как равные.
Предикат тотального порядка
Стандарт предоставляет предикат totalOrder , который определяет общее упорядочение канонических членов поддерживаемого арифметического формата. [33] Предикат согласуется с предикатами сравнения (см. раздел § Предикаты сравнения), когда одно число с плавающей точкой меньше другого. Основные отличия: [34]
- NaN можно сортировать.
- NaN рассматривается так, как если бы его абсолютное значение было больше, чем Infinity (или любые другие числа с плавающей точкой). (−NaN < −Infinity; +Infinity < +NaN.)
- qNaN и sNaN обрабатываются так, как если бы qNaN имел большее абсолютное значение, чем sNaN. (−qNaN < −sNaN; +sNaN < +qNaN.)
- Затем NaN сортируется в соответствии с полезной нагрузкой. В IEEE 754-2008 NaN с меньшей полезной нагрузкой рассматривается как имеющий меньшее абсолютное значение. В IEEE 754-2019 приемлем любой порядок, определяемый реализацией.
- Отрицательный ноль рассматривается как меньший, чем положительный ноль.
- Если обе стороны сравнения относятся к одному и тому же числу с плавающей точкой, то та часть, у которой показатель степени меньше, рассматривается как имеющая меньшее абсолютное значение. [33]
Предикат totalOrder не накладывает общего порядка на все кодировки в формате. В частности, он не различает разные кодировки одного и того же представления с плавающей точкой, как в случае, когда одна или обе кодировки неканонические. [33] IEEE 754-2019 включает разъяснения totalOrder .
Для форматов двоичного обмена, кодирование которых следует рекомендации IEEE 754-2008 по размещению сигнального бита NaN , сравнение идентично тому, которое преобразует числа с плавающей точкой в целое число со знаком и величиной (предполагая, что порядок полезной нагрузки соответствует этому сравнению), старый прием для сравнения FP без FPU. [35]
Обработка исключений
Стандарт определяет пять исключений, каждое из которых возвращает значение по умолчанию и имеет соответствующий флаг состояния, который поднимается при возникновении исключения. [g] Никакой другой обработки исключений не требуется, но рекомендуются дополнительные альтернативы, отличные от значений по умолчанию (см. § Альтернативная обработка исключений).
Пять возможных исключений:
- Недопустимая операция: математически неопределенная, например, квадратный корень отрицательного числа. По умолчанию возвращает qNaN.
- Деление на ноль: операция над конечными операндами дает точный бесконечный результат, например, 1/0 или log(0). По умолчанию возвращает ±бесконечность.
- Переполнение: конечный результат слишком велик для точного представления (т. е. его показатель степени с неограниченным диапазоном показателя будет больше emax ). По умолчанию возвращает ±бесконечность для округления до ближайшего значения (и следует правилам округления для направленных режимов округления).
- Underflow: результат очень мал (вне нормального диапазона). По умолчанию возвращает число, меньшее или равное минимальному положительному нормальному числу по величине (в соответствии с правилами округления); субнормальное число всегда подразумевает исключение Underflow, но по умолчанию, если оно точное, флаг не поднимается.
- Неточный: точный (т.е. неокругленный) результат не может быть представлен точно. По умолчанию возвращает правильно округленный результат.
Это те же пять исключений, которые были определены в IEEE 754-1985, но исключение деления на ноль было распространено на операции, отличные от деления.
Некоторые реализации десятичных чисел с плавающей точкой определяют дополнительные исключения, [36] [37], которые не являются частью IEEE 754:
- Clamped: показатель степени результата слишком велик для формата назначения. По умолчанию к коэффициенту будут добавлены конечные нули, чтобы уменьшить показатель до наибольшего используемого значения. Если это невозможно (потому что это приведет к тому, что количество необходимых цифр будет больше, чем формат назначения), то возникает исключение переполнения.
- Округлено: коэффициент результата требует больше цифр, чем предоставляет формат назначения. Неточное исключение сигнализируется, если отбрасываются любые ненулевые цифры.
Кроме того, такие операции, как квантование, когда один из операндов бесконечен или когда результат не соответствует формату назначения, также будут сигнализировать об исключении недопустимой операции. [38]
Особые ценности
Знаковый ноль
В стандарте IEEE 754 ноль имеет знак, что означает, что существуют как «положительный ноль» (+0), так и «отрицательный ноль» (−0). В большинстве сред выполнения положительный ноль обычно выводится как « 0», а отрицательный ноль как « -0». Эти два значения ведут себя как равные при числовых сравнениях, но некоторые операции возвращают разные результаты для +0 и −0. Например, 1/(−0) возвращает отрицательную бесконечность, в то время как 1/(+0) возвращает положительную бесконечность (так что сохраняется тождество 1/(1/±∞) = ±∞ ). Другие распространенные функции с разрывом при x = 0, которые могут по-разному обрабатывать +0 и −0, включают Γ ( x ) и главный квадратный корень из y + xi для любого отрицательного числа y . Как и в любой схеме приближения, операции с участием «отрицательного нуля» могут иногда вызывать путаницу. Например, в IEEE 754 x = y не всегда подразумевает 1/ x = 1/ y , так как 0 = −0, но 1/0 ≠ 1/(−0) . [39] Более того, для обратного квадратного корня rSqrt(±0) равен ±∞, в то время как математическая функция над действительными числами не имеет отрицательного значения.
Субнормальные числа
Субнормальные значения заполняют зазор под загрузкой значениями, где абсолютное расстояние между ними такое же, как и для соседних значений сразу за зазором под загрузкой. Это улучшение по сравнению со старой практикой, когда в зазоре под загрузкой был только ноль, и когда результаты под загрузкой заменялись нулем (сбрасывались на ноль). [40]
Современное оборудование для работы с числами с плавающей точкой обычно обрабатывает значения, не соответствующие норме (а также нормальные значения), и не требует программной эмуляции для значений, не соответствующих норме.
Бесконечности
Бесконечности расширенной действительной числовой строки могут быть представлены в типах данных с плавающей точкой IEEE, как и обычные значения с плавающей точкой, такие как 1, 1,5 и т. д. Они никоим образом не являются значениями ошибок, хотя они часто (в зависимости от округления) используются в качестве заменяющих значений при переполнении. При исключении деления на ноль положительная или отрицательная бесконечность возвращается как точный результат. Бесконечность также может быть представлена как число (например, макрос "INFINITY" в C или " ∞ ", если язык программирования допускает такой синтаксис).
IEEE 754 требует, чтобы бесконечностям уделялось разумное внимание, например:
- (+∞) + (+7) = (+∞)
- (+∞) × (−2) = (−∞)
- (+∞) × 0 = NaN – нет ничего осмысленного, что можно было бы сделать
NaN-ы
IEEE 754 определяет специальное значение, называемое «Не число» (NaN), которое должно быть возвращено в результате определенных «недопустимых» операций, таких как 0/0, ∞×0 или sqrt(−1). В общем случае NaN будут распространяться, т. е. большинство операций с участием NaN дадут результат NaN, хотя функции, которые дадут некоторый определенный результат для любого заданного значения с плавающей точкой, сделают это и для NaN, например NaN ^ 0 = 1. Существует два вида NaN: тихие NaN по умолчанию и, необязательно, сигнальные NaN. Сигнальный NaN в любой арифметической операции (включая числовые сравнения) вызовет сигнализацию исключения «недопустимая операция».
Представление NaN, указанное стандартом, имеет некоторые неопределенные биты, которые могут использоваться для кодирования типа или источника ошибки; но для этого кодирования нет стандарта. Теоретически, сигнализация NaN может использоваться системой выполнения для пометки неинициализированных переменных или расширения чисел с плавающей точкой другими специальными значениями без замедления вычислений с обычными значениями, хотя такие расширения не являются распространенными.
Обоснование дизайна

Распространено заблуждение, что более эзотерические особенности стандарта IEEE 754, обсуждаемые здесь, такие как расширенные форматы, NaN, бесконечности, субнормальные и т. д., представляют интерес только для численных аналитиков или для продвинутых числовых приложений. На самом деле верно обратное: эти особенности разработаны для предоставления безопасных надежных значений по умолчанию для неискушенных в числах программистов, в дополнение к поддержке сложных числовых библиотек экспертами. Главный разработчик IEEE 754 Уильям Кахан отмечает, что неправильно «... [считает] особенности стандарта IEEE 754 для двоичной арифметики с плавающей точкой, которые ... [не] оценены как особенности, пригодные для использования никем, кроме экспертов по числам. Факты совершенно противоположны. В 1977 году эти особенности были разработаны в Intel 8087 для обслуживания максимально широкого рынка... Анализ ошибок показывает нам, как разрабатывать арифметику с плавающей точкой, такую как стандарт IEEE 754, умеренно терпимую к благонамеренному невежеству среди программистов». [41]
- Специальные значения, такие как бесконечность и NaN, гарантируют, что арифметика с плавающей точкой является алгебраически полной: каждая операция с плавающей точкой дает четко определенный результат и не будет — по умолчанию — вызывать прерывание машины или ловушку. Более того, выбор специальных значений, возвращаемых в исключительных случаях, был разработан для того, чтобы во многих случаях давать правильный ответ. Например, в арифметике IEEE 754 непрерывные дроби, такие как R(z) := 7 − 3/[z − 2 − 1/(z − 7 + 10/[z − 2 − 2/(z − 3)])] дадут правильный ответ на всех входных данных, поскольку потенциальное деление на ноль, например, для z = 3 , правильно обрабатывается путем предоставления +infinity, и поэтому такие исключения можно смело игнорировать. [42] Как отметил Кахан, необработанная ловушка, последовавшая за переполнением при преобразовании числа с плавающей точкой в 16-битное целое число, которая привела к потере ракеты Ariane 5, не произошла бы при стандартной политике IEEE 754 для чисел с плавающей точкой. [41]
- Субнормальные числа гарантируют, что для конечных чисел с плавающей точкой x и y, x − y = 0 тогда и только тогда, когда x = y, как и ожидалось, но это не выполнялось в более ранних представлениях чисел с плавающей точкой. [43]
- В обосновании дизайна 80-битного формата x87 Кахан отмечает: «Этот расширенный формат предназначен для использования с незначительной потерей скорости для всех, кроме простейшей арифметики с float и double операндами. Например, его следует использовать для рабочих переменных в циклах, которые реализуют рекуррентные функции, такие как оценка полиномов, скалярные произведения, частичные и непрерывные дроби. Он часто предотвращает преждевременное переполнение/опустошение или серьезное локальное сокращение, которые могут испортить простые алгоритмы». [44] Вычисление промежуточных результатов в расширенном формате с высокой точностью и расширенной экспонентой имеет прецеденты в исторической практике научных вычислений и в разработке научных калькуляторов, например, финансовые калькуляторы Hewlett-Packard выполняли арифметические и финансовые функции с тремя значащими десятичными знаками больше, чем они хранили или отображали. [44] Реализация расширенной точности позволила легко разрабатывать стандартные элементарные библиотеки функций, которые обычно выдавали результаты двойной точности в пределах одной единицы на последнем месте (ULP) на высокой скорости.
- Правильное округление значений до ближайшего представимого значения позволяет избежать систематических смещений в расчетах и замедляет рост ошибок. Округление связей до четных устраняет статистическое смещение, которое может возникнуть при сложении похожих чисел.
- Направленное округление было задумано как помощь при проверке границ ошибок, например, в интервальной арифметике . Оно также используется при реализации некоторых функций.
- Математическая основа операций, в частности правильное округление, позволяет доказывать математические свойства и разрабатывать алгоритмы с плавающей точкой, такие как 2Sum, Fast2Sum и алгоритм суммирования Кахана , например, для повышения точности или сравнительно простой реализации арифметических подпрограмм с многократной точностью.
Свойством форматов одинарной и двойной точности является то, что их кодирование позволяет легко сортировать их без использования оборудования с плавающей точкой, как если бы биты представляли целые числа со знаком , хотя неясно, было ли это конструкционным соображением (кажется, стоит отметить, что более раннее шестнадцатеричное представление с плавающей точкой IBM также имело это свойство для нормализованных чисел). С преобладающим представлением в виде дополнения до двух интерпретация битов как целых чисел со знаком сортирует положительные числа правильно, но с обратными отрицательными; в качестве одного из возможных исправлений для этого, с помощью xor для переворота бита знака для положительных значений и всех битов для отрицательных значений, все значения становятся сортируемыми как целые числа без знака (с −0 < +0 ). [35]
Рекомендации
Альтернативная обработка исключений
Стандарт рекомендует необязательную обработку исключений в различных формах, включая предварительную подстановку определяемых пользователем значений по умолчанию, а также ловушки (исключения, которые каким-либо образом изменяют поток управления) и другие модели обработки исключений, которые прерывают поток, такие как try/catch. Ловушки и другие механизмы исключений остаются необязательными, как и в IEEE 754-1985.
Рекомендуемые операции
В пункте 9 стандарта рекомендуются дополнительные математические операции [45], которые должны определяться стандартами языка. [46] Для соответствия стандарту они не требуются.
Ниже приведены рекомендуемые арифметические операции, которые должны округляться правильно: [47]
- , ,
- , ,
- , ,
- , ,
- для (названного соединением и используемого для вычисления экспоненциального роста , скорость которого не может быть меньше −1) [48]
- ,
- , ,
- , , ,
- , , (см. также: Кратные числа π )
- , , , (см. также: Кратные числа π )
- , ,
- , ,
Функции , и не были частью стандарта IEEE 754-2008, поскольку они считались менее необходимыми. [49] и были упомянуты, но это было расценено как ошибка. [5] Все три были добавлены в редакцию 2019 года.
Рекомендуемые операции также включают установку и доступ к направлению округления динамического режима [50] и операции векторной редукции, определяемые реализацией, такие как сумма, масштабированное произведение и скалярное произведение , точность которых не указана стандартом. [51]
С 2019 года [update]также рекомендуются расширенные арифметические операции [52] для двоичных форматов. Эти операции, указанные для сложения, вычитания и умножения, производят пару значений, состоящих из результата, правильно округленного до ближайшего в формате, и погрешности, которая точно представлена в формате. На момент публикации стандарта не было известно ни одной аппаратной реализации, но очень похожие операции уже были реализованы в программном обеспечении с использованием известных алгоритмов. История и мотивация их стандартизации объясняются в справочном документе. [53] [54]
Начиная с 2019 года ранее требуемые minNum , maxNum , minNumMag и maxNumMag в IEEE 754-2008 теперь устарели из-за их неассоциативности . Вместо этого рекомендуются два набора новых минимальных и максимальных операций. [55] Первый набор содержит minimum , minimumNumber , maximum и maximumNumber . Второй набор содержит minimumMagnitude , minimumMagnitudeNumber , maximumMagnitude и maximumMagnitudeNumber . История и мотивация этого изменения объясняются в справочном документе. [56]
Оценка выражения
Стандарт рекомендует, как стандарты языка должны определять семантику последовательностей операций, и указывает на тонкости буквальных значений и оптимизаций, которые изменяют значение результата. Напротив, предыдущая версия стандарта 1985 года оставила аспекты языкового интерфейса неопределенными, что привело к непоследовательному поведению между компиляторами или различным уровням оптимизации в оптимизирующем компиляторе .
Языки программирования должны позволять пользователю указывать минимальную точность для промежуточных вычислений выражений для каждого основания. В стандарте это называется preferredWidth , и должна быть возможность устанавливать это на основе блока. Промежуточные вычисления в выражениях должны вычисляться, а любые временные значения сохраняться, используя максимальную ширину операндов и предпочтительную ширину, если она установлена. Таким образом, например, компилятор, ориентированный на оборудование с плавающей точкой x87, должен иметь средства указания того, что промежуточные вычисления должны использовать формат double-extended . Сохраненное значение переменной всегда должно использоваться при оценке последующих выражений, а не любой предшественник до округления и присвоения переменной.
Воспроизводимость
Версия стандарта IEEE 754-1985 допускала множество вариаций в реализациях (таких как кодирование некоторых значений и обнаружение определенных исключений). IEEE 754-2008 сократил эти допуски, но несколько вариаций все еще остаются (особенно для двоичных форматов). Пункт о воспроизводимости рекомендует, чтобы стандарты языка предоставляли средства для написания воспроизводимых программ (т. е. программ, которые будут выдавать тот же результат во всех реализациях языка) и описывает, что необходимо сделать для достижения воспроизводимых результатов.
Представление персонажа
Стандарт требует операций для преобразования между базовыми форматами и форматами внешней последовательности символов . [57] Преобразования в десятичный формат символов и из него требуются для всех форматов. Преобразование во внешнюю последовательность символов должно быть таким, чтобы обратное преобразование с округлением до ближайшего, с привязкой к четному восстановило исходное число. Нет требования сохранять полезную нагрузку тихого NaN или сигнального NaN, а преобразование из внешней последовательности символов может превратить сигнальный NaN в тихий NaN.
Исходное двоичное значение будет сохранено путем преобразования в десятичное и обратно с помощью: [58]
- 5 десятичных цифр для двоичного числа 16,
- 9 десятичных цифр для binary32,
- 17 десятичных цифр для binary64,
- 36 десятичных цифр для двоичного числа 128.
Для других двоичных форматов требуемое количество десятичных цифр равно [h]
где p — количество значащих бит в двоичном формате, например, 237 бит для двоичного формата 256.
При использовании десятичного формата с плавающей точкой десятичное представление будет сохранено с помощью:
- 7 десятичных цифр для decimal32,
- 16 десятичных цифр для decimal64,
- 34 десятичных знака для decimal128.
Алгоритмы с кодом для правильного округленного преобразования из двоичной системы в десятичную и из десятичной в двоичную обсуждаются Гаем [59] , а для тестирования – Паксоном и Каханом [60] .
Шестнадцатеричные литералы
Стандарт рекомендует предоставлять преобразования в и из внешних шестнадцатеричных-значимых последовательностей символов , основанных на шестнадцатеричных литералах с плавающей точкой C99 . Такой литерал состоит из необязательного знака ( +или -), индикатора "0x", шестнадцатеричного числа с точкой или без нее, индикатора экспоненты "p" и десятичной экспоненты с необязательным знаком. Синтаксис не чувствителен к регистру. [61] Десятичная экспонента масштабируется степенями 2, например, 0x0.1p-4это 1/256. [62]
Смотрите также
- формат с плавающей точкой bfloat16
- Бинаде
- Сопроцессор
- C99 для примеров кода, демонстрирующих доступ и использование функций IEEE 754
- Арифметика с плавающей точкой , для истории, обоснования конструкции и примеров использования функций IEEE 754
- Арифметика с фиксированной точкой , для альтернативного подхода к вычислениям с рациональными числами (особенно полезно, когда диапазон экспоненты известен, фиксирован или ограничен во время компиляции)
- IBM System z9 , первый процессор, реализовавший десятичную арифметику IEEE 754-2008 (с использованием аппаратного микрокода)
- IBM z10 , IBM z196 , IBM zEC12 и IBM z13 — процессоры, полностью реализующие десятичную арифметику IEEE 754-2008 на аппаратном уровне
- ISO/IEC 10967 , арифметика, не зависящая от языка (LIA)
- Minifloat , двоичные форматы с плавающей точкой низкой точности, соответствующие принципам IEEE 754
- Процессоры POWER6 , POWER7 и POWER8 , которые полностью реализуют десятичную арифметику IEEE 754-2008 на аппаратном уровне
- strictfp — устаревшее ключевое слово в языке программирования Java , которое ранее ограничивало арифметику одинарной и двойной точностью IEEE 754 для обеспечения воспроизводимости на распространенных аппаратных платформах (начиная с Java 17 такое поведение является обязательным)
- Дилемма составителя таблиц для получения дополнительной информации о правильном округлении функций
- Стандартная числовая среда Apple
- Конусная плавающая точка
- Posit , альтернативный числовой формат
Примечания
- ^ Например, если основание равно 10, знак равен 1 (указывает на отрицательность), мантисса равна 12345, а показатель степени равен −3, то значение числа равно (−1) 1 × 12345 × 10 −3 = −1 × 12345 × 0,001 = −12,345.
- ^ Приблизительные значения. Точные значения см. в отдельной статье Википедии для каждого формата.
- ^ Количество цифр в используемом основании системы счисления, включая любые неявные цифры, но не считая знакового бита.
- ^ Соответствующее количество десятичных цифр см. в тексте для получения более подробной информации.
- ^ В отличие от десятичной системы, двоичного формата обмена длиной 96 бит не существует. Однако такой формат все еще допускается как необменный формат.
- ^ Стандарт рекомендует использовать 0 для сигнальных NaN, 1 — для тихих NaN, так что сигнальный NaN можно заглушить, изменив только этот бит на 1, в то время как обратное может привести к кодированию бесконечности.
- ^ В некоторых случаях переполнения флаг не поднимается.
- ^ В качестве ограничения реализации правильное округление гарантируется только для требуемого количества десятичных цифр плюс 3 для наибольшего поддерживаемого двоичного формата. Например, если binary32 является наибольшим поддерживаемым двоичным форматом, то преобразование из десятичной внешней последовательности с 12 десятичными цифрами гарантированно будет правильно округлено при преобразовании в binary32; но преобразование последовательности из 13 десятичных цифр — нет; однако стандарт рекомендует, чтобы реализации не налагали такого ограничения.
Ссылки
- ^ IEEE 754 2019
- ^ Хаас, Джоди. "FW: ISO/IEC/IEEE 60559 (IEEE Std 754-2008)". IEEE . Архивировано из оригинала 2017-10-27 . Получено 2018-04-04 .
- ^ "Соглашение о сотрудничестве между организациями по разработке стандартов ISO/IEEE (PSDO)" (PDF) . ISO. 2007-12-19 . Получено 2021-12-27 .
- ^ ISO/IEC JTC 1/SC 25 2011.
- ^ ab Cowlishaw, Mike (2013-11-13). "IEEE 754-2008 errata". speleotrove.com . Получено 2020-01-24 .
- ^ "ANSI/IEEE Std 754-2019". ucbtest.org . Получено 2024-01-16 .
- ^ ISO/IEC JTC 1/SC 25 2020.
- ^ "Проблемы для следующей ревизии 754". IEEE . Получено 2024-08-12 .
- ^ IEEE 754 2008, §2.1.27.
- ^ "SpiderMonkey Internals". udn.realityripple.com . Получено 2018-03-11 .
- ^ Клеменс, Бен (сентябрь 2014 г.). 21-й век C: Советы по C от Новой Школы. O'Reilly Media, Incorporated. стр. 160. ISBN 9781491904442. Получено 11.03.2018 .
- ^ "zuiderkwast/nanbox: NaN-бокс в C" . Гитхаб . Проверено 11 марта 2018 г.
- ^ IEEE 754 2008, §3.6.
- ^ IEEE 754 2008, §3.7.
- ^ IEEE 754 2008, §3.7 гласит: «Стандарты языка должны определять механизмы, поддерживающие расширяемую точность для каждого поддерживаемого основания».
- ^ IEEE 754 2008, §3.7 гласит: «Стандарты или реализации языка должны поддерживать расширенный формат точности, который расширяет самый широкий базовый формат, поддерживаемый в этом основании».
- ^ Motorola MC68000 Family (PDF) . Справочное руководство программиста. NXP Semiconductors. 1992. С. 1–16, 1–18, 1–23.
- ^ IEEE 754 2008, §4.3.1. «В следующих двух атрибутах направления округления бесконечно точный результат с величиной не менее должен округляться до без изменения знака».
- ^ IEEE 754 2008, §4.3.3
- ^ IEEE 754 2019, §2.1
- ^ abc IEEE 754 2008, §5.3.1
- ^ Согласно IEEE 754 2008, §5.4.1
- ^ IEEE 754 2008, §5.4.2
- ^ IEEE 754 2008, §5.4.3
- ^ IEEE 754 2008, §5.3.2
- ^ IEEE 754 2008, §5.3.3
- ^ IEEE 754 2008, §5.5.1
- ^ IEEE 754 2008, §5.10
- ^ IEEE 754 2008, §5.11
- ^ IEEE 754 2008, §5.7.2
- ^ IEEE 754 2008, §5.7.4
- ^ IEEE 754 2019, §5.11
- ^ abc IEEE 754 2019, §5.10
- ^ "Реализация total_cmp для f32, f64 от golddranks · Запрос на извлечение № 72568 · rust-lang/rust". GitHub .– содержит соответствующие цитаты из IEEE 754-2008 и -2019. Содержит реализацию и объяснение каламбуров.
- ^ ab Herf, Michael (декабрь 2001 г.). "radix tricks". stereopsis: graphics .
- ^ "9.4. decimal — Десятичная арифметика с фиксированной и плавающей точкой — Документация Python 3.6.5". docs.python.org . Получено 2018-04-04 .
- ^ "Десятичная арифметика - Исключительные условия". speleotrove.com . Получено 2018-04-04 .
- ^ IEEE 754 2008, §7.2(h)
- ^ Голдберг 1991.
- ^ Мюллер, Жан-Мишель; Бризебар, Николя; де Динешен, Флоран; Жаннерод, Клод-Пьер; Лефевр, Винсент; Мелькионд, Гийом; Револь, Натали ; Стеле, Дэмиен; Торрес, Серж (2010). Справочник по арифметике с плавающей запятой (1-е изд.). Биркхойзер . дои : 10.1007/978-0-8176-4705-6. ISBN 978-0-8176-4704-9. LCCN 2009939668.
- ^ ab Kahan, William Morton ; Darcy, Joseph (2001) [1998-03-01]. "Как плавающая точка Java вредит всем и везде" (PDF) . Архивировано (PDF) из оригинала 2000-08-16 . Получено 2003-09-05 .
- ^ Кахан, Уильям Мортон (1981-02-12). "Зачем нам нужен стандарт арифметики с плавающей точкой?" (PDF) . стр. 26. Архивировано (PDF) из оригинала 2004-12-04.
- ↑ Северанс, Чарльз (20.02.1998). «Интервью со стариком плавающей точки».
- ^ ab Kahan, William Morton (1996-06-11). "Пагубное воздействие компьютерных тестов на прикладную математику, физику и химию" (PDF) . Архивировано (PDF) из оригинала 2013-10-13.
- ^ IEEE 754 2019, §9.2
- ^ IEEE 754 2008, Статья 9
- ^ IEEE 754 2019, §9.2.
- ^ "Слишком много мощности - pow против powr, powd, pown, rootn, composite". IEEE . Получено 2024-01-16 .
Поскольку темпы роста не могут быть меньше -1, такие темпы сигнализируют о недопустимых исключениях.
- ^ "Re: Отсутствуют функции tanPi, asinPi и acosPi". IEEE . Архивировано из оригинала 2017-07-06 . Получено 2018-04-04 .
- ^ IEEE 754 2008, §9.3.
- ^ IEEE 754 2008, §9.4.
- ^ IEEE 754 2019, §9.5
- ^ Риди, Джейсон; Деммел, Джеймс. «Расширенные арифметические операции, предложенные для IEEE-754 2018» (PDF) . 25-й симбозиум IEEE по компьютерной арифметике (ARITH 2018). стр. 49–56. Архивировано (PDF) из оригинала 23-07-2019 . Получено 23-07-2019 .
- ^ "ANSI/IEEE Std 754-2019 – Справочные документы". IEEE . Получено 2024-01-16 .
- ^ IEEE 754 2019, §9.6.
- ^ Чен, Дэвид. «Удаление/понижение операций MinNum и MaxNum из IEEE 754-2018» (PDF) . IEEE . Получено 16.01.2024 .
- ^ IEEE 754 2008, §5.12.
- ^ IEEE 754 2008, §5.12.2.
- ^ Гей, Дэвид М. (1990-11-30), Правильно округленные двоично-десятичные и десятично-двоичные преобразования, Numerical Analysis Manuscript, Murry Hill, NJ, US: AT&T Laboratories, 90-10
- ^ Paxson, Vern; Kahan, William (1991-05-22), Программа для тестирования преобразования десятичной системы счисления в двоичную , рукопись, CiteSeerX 10.1.1.144.5889
- ^ IEEE 754 2008, §5.12.3
- ^ "6.9.3. Шестнадцатеричные литералы с плавающей точкой — Руководство пользователя Glasgow Haskell Compiler 9.3.20220129". ghc.gitlab.haskell.org . Получено 29.01.2022 .
Стандарты
- Стандарт IEEE для двоичной арифметики с плавающей точкой . ANSI/IEEE STD 754-1985. IEEE. 1985-10-12. стр. 1–20. doi :10.1109/IEEESTD.1985.82928. ISBN 0-7381-1165-1.
- IEEE Computer Society (29.08.2008). Стандарт IEEE для арифметики с плавающей точкой . IEEE STD 754-2008. IEEE. стр. 1–70. doi :10.1109/IEEESTD.2008.4610935. ISBN 978-0-7381-5753-5. Стандарт IEEE 754-2008.
- IEEE Computer Society (2019-07-22). Стандарт IEEE для арифметики с плавающей точкой . IEEE STD 754-2019. IEEE. стр. 1–84. doi :10.1109/IEEESTD.2019.8766229. ISBN 978-1-5044-5924-2. Стандарт IEEE 754-2019.
- ISO/IEC JTC 1/SC 25 (июнь 2011 г.). ISO/IEC/IEEE 60559:2011 — Информационные технологии — Микропроцессорные системы — Арифметика с плавающей точкой. ISO. С. 1–58.
{{cite book}}: CS1 maint: numeric names: authors list (link) - ISO/IEC JTC 1/SC 25 (май 2020 г.). ISO/IEC 60559:2020 — Информационные технологии — Микропроцессорные системы — Арифметика с плавающей точкой . ISO. С. 1–74.
{{cite book}}: CS1 maint: numeric names: authors list (link)
Вторичные ссылки
- Десятичная арифметика с плавающей точкой, часто задаваемые вопросы, библиография и ссылки
- Сравнение двоичных чисел с плавающей точкой
- Справочный материал IEEE 754
- IEEE 854-1987 – История и протоколы
- Дополнительные материалы для чтения по IEEE 754. Включает исторические перспективы.
Дальнейшее чтение
- Голдберг, Дэвид (март 1991 г.). «Что каждый специалист по компьютерам должен знать об арифметике с плавающей точкой». ACM Computing Surveys . 23 (1): 5–48. doi : 10.1145/103162.103163 . S2CID 222008826.(С приложением «Различия между реализациями IEEE 754»: [1], [2])
- Хеккер, Крис (февраль 1996 г.). «Давайте перейдем к (плавающей) точке» (PDF) . Game Developer Magazine : 19–24. ISSN 1073-922X.
- Severance, Charles (март 1998 г.). «IEEE 754: интервью с Уильямом Кэханом» (PDF) . IEEE Computer . 31 (3): 114–115. doi :10.1109/MC.1998.660194. S2CID 33291145 . Получено 08.03.2019 .
- Cowlishaw, Mike (июнь 2003 г.). «Десятичные числа с плавающей точкой: алгоритмы для компьютеров». 16-й симпозиум IEEE по компьютерной арифметике, 2003 г. Труды (PDF) . Лос-Аламитос, Калифорния: IEEE Computer Society. стр. 104–111. doi :10.1109/ARITH.2003.1207666. ISBN 978-0-7695-1894-7. S2CID 18713046 . Получено 14.11.2014 .. (Примечание: Алгоризм — это не неправильное написание названия; см. также algorism .)
- Monniaux, David (май 2008). «Подводные камни проверки вычислений с плавающей точкой». ACM Transactions on Programming Languages and Systems . 30 (3): 1–41. arXiv : cs/0701192 . doi :10.1145/1353445.1353446. ISSN 0164-0925. S2CID 218578808.: Сборник неинтуитивных поведений вычислений с плавающей точкой на популярных архитектурах, имеющих значение для проверки и тестирования программ.
- Мюллер, Жан-Мишель; Бруни, Николас; де Динешен, Флоран; Жаннерод, Клод-Пьер; Джолдес, Миоара; Лефевр, Винсент; Мелькионд, Гийом; Револь, Натали ; Торрес, Серж (2018) [2010]. Справочник по арифметике с плавающей запятой (2-е изд.). Биркхойзер . дои : 10.1007/978-3-319-76526-6. ISBN 978-3-319-76525-9.
- Overton, Michael L. (2001). Написано в Courant Institute of Mathematical Sciences , New York University , Нью-Йорк, США. Numerical Computing with IEEE Floating Point Arithmetic (1-е изд.). Филадельфия, США: SIAM . doi :10.1137/1.9780898718072. ISBN 978-0-89871-482-1. 978-0-89871-571-2, 0-89871-571-7.
- Клив Молер о числах с плавающей точкой
- Beebe, Nelson HF (2017-08-22). Справочник по вычислению математических функций — программирование с использованием библиотеки переносимого программного обеспечения MathCW (1-е изд.). Солт-Лейк-Сити, Юта, США: Springer International Publishing AG . doi :10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721.
- Хаф, Дэвид Г. (декабрь 2019 г.). «Стандарт IEEE 754: один для исторических книг». Компьютер . 52 (12). IEEE : 109–112. doi : 10.1109/MC.2019.2926614. S2CID 208281213.
Внешние ссылки
- Кахан о создании стандарта IEEE с плавающей точкой. Клипы лауреатов премии Тьюринга . 2020-11-16. Архивировано из оригинала 2021-11-08.



![{\displaystyle 1{\big ][\sqrt {x{\vphantom {t}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c66dfb8a01ec56a4466acddaaec60a62381f1a1)













































