преобразование Хафа
| Обнаружение особенностей |
|---|
| Обнаружение краев |
| Обнаружение угла |
| Обнаружение пятен |
| Ridge detection |
| Hough transform |
|
| Structure tensor |
| Affine invariant feature detection |
| Feature description |
| Scale space |
Преобразование Хафа — это метод извлечения признаков, используемый в анализе изображений , компьютерном зрении , распознавании образов и цифровой обработке изображений . [1] [2] Целью метода является поиск несовершенных экземпляров объектов в пределах определенного класса форм с помощью процедуры голосования. Эта процедура голосования выполняется в пространстве параметров , из которого кандидаты на объекты получаются как локальные максимумы в так называемом пространстве аккумуляторов, которое явно строится алгоритмом для вычисления преобразования Хафа.
Классическое преобразование Хафа было связано с идентификацией линий на изображении, но позже преобразование Хафа было расширено для идентификации положений произвольных форм, чаще всего кругов или эллипсов . Преобразование Хафа, в том виде, в котором оно используется сегодня, было изобретено Ричардом Дудой и Питером Хартом в 1972 году, которые назвали его «обобщенным преобразованием Хафа» [3] в честь соответствующего патента 1962 года Пола Хафа. [4] [5] Преобразование было популяризировано в сообществе компьютерного зрения Даной Х. Баллардом через журнальную статью 1981 года под названием « Обобщение преобразования Хафа для обнаружения произвольных форм ».
История
Первоначально он был изобретен для машинного анализа фотографий, полученных с помощью пузырьковой камеры (Хаф, 1959).
Преобразование Хафа было запатентовано в качестве патента США 3,069,654 в 1962 году и передано Комиссии по атомной энергии США под названием «Метод и средства распознавания сложных шаблонов». Этот патент использует параметризацию наклона-пересечения для прямых линий, что неудобно приводит к неограниченному пространству преобразования, поскольку наклон может стремиться к бесконечности.
Параметризация rho–theta, которая сегодня используется повсеместно, была впервые описана в
- Дуда, РО; Харт, П.Е. (январь 1972 г.). «Использование преобразования Хафа для обнаружения линий и кривых на изображениях». Comm. ACM . 15 : 11– 15. doi : 10.1145/361237.361242 . S2CID 1105637.
хотя это было стандартом для преобразования Радона , по крайней мере, с 1930-х годов.
Вариант О'Гормана и Клоуза описан в
- О'Горман, Фрэнк; Клоуз, МБ (1976). «Нахождение краев изображения с помощью коллинеарности точек объектов». IEEE Trans. Comput . 25 (4): 449– 456. doi :10.1109/TC.1976.1674627. S2CID 10851078.
История изобретения современной формы преобразования Хафа изложена в
- Hart, PE (ноябрь 2009 г.). «Как было изобретено преобразование Хафа» (PDF) . Журнал обработки сигналов IEEE . 26 (6): 18– 22. doi :10.1109/msp.2009.934181. S2CID 16245096. Архивировано из оригинала (PDF) 2018-05-16.
Теория
При автоматическом анализе цифровых изображений часто возникает подзадача обнаружения простых форм, таких как прямые линии, окружности или эллипсы. Во многих случаях детектор краев может использоваться в качестве этапа предварительной обработки для получения точек изображения или пикселей изображения, которые находятся на желаемой кривой в пространстве изображения. Однако из-за несовершенств либо в данных изображения, либо в детекторе краев могут быть пропущенные точки или пиксели на желаемых кривых, а также пространственные отклонения между идеальной линией/окружностью/эллипсом и зашумленными точками края, полученными от детектора краев. По этим причинам часто бывает нетривиально сгруппировать извлеченные характеристики края в соответствующий набор линий, окружностей или эллипсов. Целью преобразования Хафа является решение этой проблемы, позволяя выполнять группировки точек края в кандидатов на объекты путем выполнения явной процедуры голосования по набору параметризованных объектов изображения (Шапиро и Стокман, 304).
Обнаружение линий
Простейшим случаем преобразования Хафа является обнаружение прямых линий. В общем случае прямая линия y = mx + b может быть представлена как точка ( b , m ) в пространстве параметров. Однако вертикальные линии представляют собой проблему. Они могут привести к неограниченным значениям параметра наклона m . Таким образом, по вычислительным причинам Дуда и Харт [6] предложили использовать нормальную форму Гессе
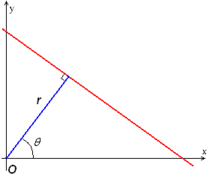
где — расстояние от начала координат до ближайшей точки на прямой, а — угол между осью и линией, соединяющей начало координат с этой ближайшей точкой.
Интуиция для этой формы, подобно уравнению плоскости, заключается в том, что каждый вектор на линии должен быть перпендикулярен (ортогонален) прямой линии длины , которая исходит из начала координат. Можно видеть, что точка пересечения функциональной линии и перпендикулярной линии, которая исходит из начала координат, находится в . Таким образом, для любой точки на линии вектор должен быть ортогонален вектору . Следовательно, мы получаем, что для любой точки на функциональной линии уравнение должно быть удовлетворено. Следовательно, . Поскольку и , мы получаем . Поскольку , мы получаем окончательную форму .
Поэтому можно связать с каждой линией изображения пару . Плоскость иногда называют пространством Хафа для множества прямых линий в двух измерениях. Такое представление делает преобразование Хафа концептуально очень близким к двумерному преобразованию Радона . Фактически, преобразование Хафа математически эквивалентно преобразованию Радона, но эти два преобразования имеют различные вычислительные интерпретации, традиционно связанные с ними. [7]
Если задана одна точка на плоскости, то набор всех прямых линий, проходящих через эту точку, соответствует синусоидальной кривой в плоскости ( r , θ ), которая уникальна для этой точки. Набор из двух или более точек, образующих прямую линию, создаст синусоиды, пересекающиеся в точке ( r , θ ) для этой линии. Таким образом, задача обнаружения коллинеарных точек может быть преобразована в задачу поиска конкурирующих кривых .
Вероятностная интерпретация
При наличии формы, параметризованной с помощью , принимающей значения в наборе , называемом пространством формы, можно интерпретировать преобразование Хафа как обратное преобразование распределения вероятностей в пространстве изображения в пространство формы и интерпретировать обнаружение формы как оценку максимального правдоподобия .
Явно преобразование Хафа выполняет приближенный наивный байесовский вывод. Мы начинаем с однородного априорного значения в пространстве форм. Мы рассматриваем только положительные свидетельства и игнорируем все отрицательные свидетельства, чтобы мы могли обнаружить частично закрытые формы.
Мы суммируем логарифмическое правдоподобие в пространстве формы до аддитивной константы. Предположение наивного Байеса означает, что все пиксели в пространстве изображения предоставляют независимые свидетельства, так что их правдоподобия умножаются, то есть их логарифмические правдоподобия складываются. Свобода в аддитивной константе позволяет нам не выполнять никаких операций над «фоновыми пикселями» в пространстве формы.
Наконец, мы выполняем оценку максимального правдоподобия, выбирая пики в логарифмическом правдоподобии на пространстве форм. [8]
Производные
Выполнение
Алгоритм линейного преобразования Хафа оценивает два параметра, которые определяют прямую линию. Пространство преобразования имеет два измерения, и каждая точка в пространстве преобразования используется как аккумулятор для обнаружения или идентификации линии, описанной . Каждая точка в обнаруженных краях на изображении вносит вклад в аккумуляторы.
Размерность аккумулятора равна числу неизвестных параметров, т. е. двум, учитывая квантованные значения и в паре . Для каждого пикселя в и его окрестности алгоритм преобразования Хафа определяет, достаточно ли доказательств прямой линии в этом пикселе. Если да, он вычисляет параметры этой линии, затем ищет ячейку аккумулятора, в которую попадают параметры, и увеличивает значение этой ячейки.
Находя ячейки с наивысшими значениями, как правило, путем поиска локальных максимумов в пространстве аккумулятора, можно извлечь наиболее вероятные линии и считать их (приблизительные) геометрические определения (Шапиро и Стокман, 304). Самый простой способ найти эти пики — применить некоторую форму порога, но другие методы могут дать лучшие результаты в других обстоятельствах — определить, какие линии найдены, а также сколько. Поскольку возвращаемые линии не содержат никакой информации о длине, часто необходимо на следующем этапе найти, какие части изображения соответствуют каким линиям. Более того, из-за ошибок несовершенства на этапе обнаружения краев, как правило, будут ошибки в пространстве аккумулятора, что может сделать нетривиальным поиск соответствующих пиков и, следовательно, соответствующих линий.
Конечный результат линейного преобразования Хафа — двумерный массив (матрица), аналогичный аккумулятору — одно измерение этой матрицы — квантованный угол , а другое измерение — квантованное расстояние . Каждый элемент матрицы имеет значение, равное сумме точек или пикселей, которые расположены на линии, представленной квантованными параметрами . Таким образом, элемент с наибольшим значением указывает на прямую линию, которая наиболее представлена во входном изображении. [9]
Примеры
Пример 1
Рассмотрим три точки данных, показанные здесь черными точками.

- Для каждой точки данных строится ряд линий, проходящих через нее, все под разными углами. Они показаны здесь разными цветами.
- Преобразование Хафа накапливает вклады от всех пикселей в обнаруженном крае. Для каждой линии существует опорная линия, которая перпендикулярна ей и пересекает начало координат . В каждом случае одна из них показана в виде стрелки.
- Рассчитывается длина (т.е. перпендикулярное расстояние до начала координат) и угол каждой опорной линии. Длины и углы приведены в таблицах под диаграммами.
Из расчетов видно, что в обоих случаях опорная линия в 60° имеет схожую длину. Отсюда следует, что соответствующие линии (синие на рисунке выше) очень похожи. Таким образом, можно предположить, что все точки лежат близко к синей линии.
Пример 2
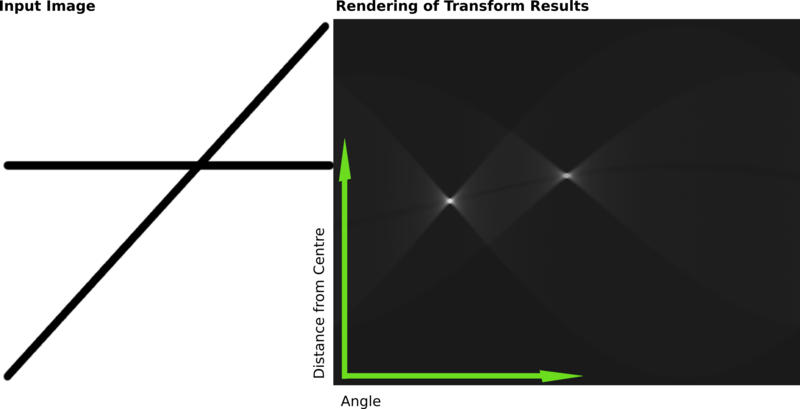
Ниже приведен другой пример, демонстрирующий результаты преобразования Хафа на растровом изображении, содержащем две толстые линии.
Результаты этого преобразования были сохранены в матрице. Значение ячейки представляет собой количество кривых, проходящих через любую точку. Более высокие значения ячейки отображаются ярче. Два отчетливо ярких пятна являются параметрами Хафа двух линий. Из положений этих пятен можно определить угол и расстояние от центра изображения двух линий на входном изображении.
Вариации и расширения
Использование направления градиента для уменьшения количества голосов
Улучшение, предложенное О'Горманом и Клоузом, может быть использовано для обнаружения линий, если принять во внимание, что локальный градиент интенсивности изображения обязательно будет ортогонален краю. Поскольку обнаружение края обычно включает вычисление величины градиента интенсивности, направление градиента часто находится как побочный эффект. Если заданная точка координат ( x,y ) действительно находится на линии, то локальное направление градиента дает параметр θ , соответствующий указанной линии, и затем немедленно получается параметр r . (Шапиро и Стокман, 305) Направление градиента можно оценить с точностью до 20°, что сокращает след синусоиды с полных 180° до примерно 45°. Это сокращает время вычислений и имеет интересный эффект сокращения количества бесполезных голосов, тем самым улучшая видимость пиков, соответствующих реальным линиям на изображении.
Преобразование Хафа на основе ядра (KHT)
Фернандес и Оливейра [10] предложили улучшенную схему голосования для преобразования Хафа, которая позволяет программной реализации достигать производительности в реальном времени даже на относительно больших изображениях (например, 1280×960). Преобразование Хафа на основе ядра использует ту же параметризацию, предложенную Дудой и Хартом, но работает с кластерами приблизительно коллинеарных пикселей. Для каждого кластера голоса подаются с использованием ориентированного эллиптического гауссовского ядра, которое моделирует неопределенность, связанную с наиболее подходящей линией относительно соответствующего кластера. Такой подход не только значительно улучшает производительность схемы голосования, но и создает гораздо более чистый аккумулятор и делает преобразование более устойчивым к обнаружению ложных линий.
Трехмерное преобразование Хафа на основе ядра для обнаружения плоскости (3DKHT)
Лимбергер и Оливейра [11] предложили детерминированный метод обнаружения плоскости в неорганизованных облаках точек, стоимость которого определяется числом образцов, достигая производительности в реальном времени для относительно больших наборов данных (до точек на процессоре 3,4 ГГц). Он основан на быстрой стратегии голосования преобразования Хафа для плоских областей, вдохновленной преобразованием Хафа на основе ядра (KHT). Это трехмерное преобразование Хафа на основе ядра (3DKHT) использует быстрый и надежный алгоритм для сегментации кластеров приблизительно копланарных образцов и отдает голоса за отдельные кластеры (вместо отдельных образцов) на ( ) сферическом аккумуляторе с использованием трехмерного гауссова ядра. Этот подход на несколько порядков быстрее существующих (недетерминированных) методов обнаружения плоскости в облаках точек, таких как RHT и RANSAC , и лучше масштабируется с размером наборов данных. Его можно использовать с любым приложением, требующим быстрого обнаружения плоских объектов в больших наборах данных.
Преобразование Хафа кривых и его обобщение для аналитических и неаналитических форм
Хотя версия преобразования, описанная выше, применима только для поиска прямых линий, аналогичное преобразование можно использовать для поиска любой формы, которая может быть представлена набором параметров. Например, окружность можно преобразовать в набор из трех параметров, представляющих ее центр и радиус, так что пространство Хафа становится трехмерным. Произвольные эллипсы и кривые также можно найти таким образом, как и любую форму, легко выраженную в виде набора параметров.
Обобщение преобразования Хафа для обнаружения аналитических фигур в пространствах любой размерности было предложено Фернандесом и Оливейрой. [12] В отличие от других подходов, основанных на преобразовании Хафа для аналитических фигур, метод Фернандеса не зависит от формы, которую нужно обнаружить, или от типа входных данных. Обнаружение может быть приведено к типу аналитической фигуры путем изменения предполагаемой модели геометрии, в которой были закодированы данные (например, евклидово пространство , проективное пространство , конформная геометрия и т. д.), в то время как предложенная формулировка остается неизменной. Кроме того, она гарантирует, что предполагаемые фигуры представлены с наименьшим возможным числом параметров, и позволяет одновременно обнаруживать различные виды фигур, которые наилучшим образом соответствуют входному набору записей с различной размерностью и различными геометрическими определениями (например, одновременное обнаружение плоскостей и сфер, которые наилучшим образом соответствуют набору точек, прямых линий и окружностей).
Для более сложных фигур на плоскости (т. е. фигур, которые не могут быть представлены аналитически в каком-либо двумерном пространстве) используется обобщенное преобразование Хафа [13] , которое позволяет объекту голосовать за определенное положение, ориентацию и/или масштабирование фигуры с использованием предопределенной таблицы соответствия. Преобразование Хафа накапливает вклады всех пикселей в обнаруженном крае.
Процесс обнаружения круга
Изменить алгоритм для обнаружения круговых фигур вместо линий сравнительно просто.
- Сначала мы создаем пространство аккумулятора, которое состоит из ячейки для каждого пикселя. Изначально каждая ячейка установлена на 0.
- Для каждой точки края (i, j) на изображении прирастить все ячейки, которые согласно уравнению окружности могли бы быть центром окружности. Эти ячейки представлены буквой в уравнении.
- Для каждого возможного значения , найденного на предыдущем шаге, найдите все возможные значения , которые удовлетворяют уравнению.
- Поиск локальных максимумов в пространстве аккумулятора. Эти ячейки представляют собой круги, обнаруженные алгоритмом.
Если мы заранее не знаем радиус окружности, которую пытаемся найти, мы можем использовать трехмерное пространство аккумуляторов для поиска окружностей с произвольным радиусом. Естественно, это более затратно с точки зрения вычислений.
Этот метод также позволяет обнаруживать круги, которые частично находятся за пределами пространства аккумулятора, при условии, что внутри него все еще находится достаточная часть площади круга.
Обнаружение 3D-объектов (плоскостей и цилиндров)
Преобразование Хафа также может использоваться для обнаружения 3D-объектов в данных диапазона или 3D- облаках точек . Расширение классического преобразования Хафа для обнаружения плоскости довольно простое. Плоскость представлена ее явным уравнением , для которого мы можем использовать 3D-пространство Хафа, соответствующее , и . Это расширение страдает от тех же проблем, что и его 2D-аналог, т. е. почти горизонтальные плоскости могут быть надежно обнаружены, в то время как производительность ухудшается, когда плоскостное направление становится вертикальным (большие значения и усиливают шум в данных). Эта формулировка плоскости использовалась для обнаружения плоскостей в облаках точек, полученных с помощью воздушного лазерного сканирования [14], и работает очень хорошо, потому что в этой области все плоскости почти горизонтальны.
Для обобщенного обнаружения плоскости с использованием преобразования Хафа плоскость может быть параметризована ее нормальным вектором (с использованием сферических координат) и ее расстоянием от начала координат, что приводит к трехмерному пространству Хафа. Это приводит к тому, что каждая точка во входных данных голосует за синусоидальную поверхность в пространстве Хафа. Пересечение этих синусоидальных поверхностей указывает на наличие плоскости. [15] Более общий подход для более чем 3 измерений требует эвристики поиска, чтобы оставаться осуществимым. [16]
Преобразование Хафа также использовалось для поиска цилиндрических объектов в облаках точек с использованием двухэтапного подхода. Первый шаг находит ориентацию цилиндра, а второй шаг находит положение и радиус. [17]
Использование взвешенных характеристик
Одна общая деталь вариации. То есть, нахождение ячеек с наибольшим количеством на одном этапе может быть использовано для ограничения диапазона значений, искомых на следующем этапе.
Тщательно выбранное пространство параметров
Пространство параметров высокой размерности для преобразования Хафа не только медленное, но и при необдуманной реализации может легко переполнить доступную память. Даже если среда программирования позволяет выделять массив, больший, чем доступное пространство памяти, через виртуальную память, количество страниц , необходимых для этого, будет очень большим, поскольку массив накопителя используется в режиме случайного доступа, редко останавливаясь в смежной памяти, поскольку он переходит от индекса к индексу.
Рассмотрим задачу поиска эллипсов на изображении 800x600. Предполагая, что радиусы эллипсов ориентированы вдоль главных осей, пространство параметров является четырехмерным. ( x , y ) определяет центр эллипса, а a и b обозначают два радиуса. Допуская, что центр может находиться в любом месте изображения, добавляем ограничение 0 < x < 800 и 0 < y < 600. Если радиусам задать те же значения, что и ограничениям, то останется разреженно заполненный массив аккумуляторов из более чем 230 миллиардов значений.
Программа, задуманная таким образом, вряд ли сможет выделить достаточно памяти. Это не значит, что проблема не может быть решена, а лишь то, что должны быть найдены новые способы ограничения размера массива аккумуляторов, что делает это осуществимым. Например:
- Если разумно предположить, что каждый из эллипсов полностью содержится в изображении, диапазон радиусов может быть уменьшен. Наибольший радиус может быть, если центр эллипса находится в центре изображения, позволяя краям эллипса растягиваться до краев. В этом экстремальном случае радиусы могут быть только в два раза меньше размера изображения, ориентированного в одном направлении. Уменьшение диапазона a и b таким образом уменьшает массив аккумулятора до 57 миллиардов значений.
- Пожертвуйте точностью ради пространства при оценке центра: если прогнозируется, что центр сместится на 3 единицы как по оси x, так и по оси y, это уменьшит размер массива аккумулятора примерно до 6 миллиардов значений.
- Точность в обмен на пространство при оценке радиусов: если радиусы оцениваются с ошибкой в 5, происходит дальнейшее уменьшение размера массива аккумуляторов примерно на 256 миллионов значений.
- Обрежьте изображение до интересующих областей. Это зависит от изображения и, следовательно, непредсказуемо, но представьте себе случай, когда все интересующие края изображения находятся в верхнем левом квадранте этого изображения. Массив аккумуляторов в этом случае можно уменьшить еще больше, ограничив все 4 параметра коэффициентом 2, что даст общий коэффициент уменьшения 16.
Применив только первые три из этих ограничений к приведенному примеру, размер массива аккумуляторов сокращается почти в 1000 раз, что позволяет уменьшить его до размера, который с гораздо большей вероятностью поместится в памяти современного компьютера.
Эффективный алгоритм обнаружения эллипса
Юнхун Се и Цян Цзи предлагают эффективный способ реализации преобразования Хафа для обнаружения эллипсов, преодолевая проблемы с памятью. [18] Как обсуждалось в алгоритме (на странице 2 статьи), этот подход использует только одномерный аккумулятор (для малой оси) для обнаружения эллипсов на изображении. Сложность составляет O(N 3 ) по количеству ненулевых точек на изображении.
Ограничения
Преобразование Хафа эффективно только в том случае, если большое количество голосов попадает в правую ячейку, так что ячейку можно легко обнаружить на фоне фонового шума. Это означает, что ячейка не должна быть слишком маленькой, иначе некоторые голоса попадут в соседние ячейки, тем самым уменьшая видимость основной ячейки. [19]
Кроме того, когда число параметров велико (то есть когда мы используем преобразование Хафа с обычно более чем тремя параметрами), среднее число голосов, поданных в одном бине, очень мало, и те бины, которые соответствуют реальной фигуре на изображении, не обязательно имеют гораздо большее число голосов, чем их соседи. Сложность увеличивается со скоростью с каждым дополнительным параметром, где — размер пространства изображения, а — число параметров. (Шапиро и Стокман, 310) Таким образом, преобразование Хафа должно использоваться с большой осторожностью, чтобы обнаружить что-либо, кроме линий или кругов.
Наконец, большая часть эффективности преобразования Хафа зависит от качества входных данных: края должны быть хорошо обнаружены, чтобы преобразование Хафа было эффективным. Использование преобразования Хафа на зашумленных изображениях — очень деликатный вопрос, и, как правило, перед этим необходимо использовать этап шумоподавления. В случае, когда изображение искажено спеклами, как в случае с радиолокационными изображениями, преобразование Радона иногда предпочтительнее для обнаружения линий, поскольку оно ослабляет шум посредством суммирования.
Смотрите также
- Обобщенное преобразование Хафа
- Рандомизированное преобразование Хафа
- Радоновое преобразование
- преобразование Фурье
Ссылки
- ^ Шапиро, Линда и Стокман, Джордж. «Компьютерное зрение», Prentice-Hall, Inc. 2001
- ^ Романенго, Кьяра; Фальчидиено, Бьянка; Биасотти, Сильвия (2024-09-01). «Расширение преобразования Хафа для распознавания и аппроксимации пространственных кривых в 3D-моделях». Computer Aided Geometric Design . 113 : 102377. doi : 10.1016/j.cagd.2024.102377 . ISSN 0167-8396.
- ↑ Дуда, РО и П.Е. Харт, «Использование преобразования Хафа для обнаружения линий и кривых на изображениях», Comm. ACM , т. 15, стр. 11–15 (январь 1972 г.).
- ^ Хаф, ПВХ Метод и средства распознавания сложных узоров , Патент США 3,069,654, 18 декабря 1962 г.
- ^ ПВХ Хаф, Машинный анализ изображений пузырьковой камеры , Труды Международной конференции по ускорителям и приборам высоких энергий, 1959.
- ^ Ричард О. Дуда ; Питер Э. Харт (апрель 1971 г.). «Использование преобразования Хафа для обнаружения линий и кривых на изображениях» (PDF) . Центр искусственного интеллекта .
- ^ Краткое введение в преобразования Радона и Хафа и их взаимосвязь. CiteSeerX.
- ^ Стивенс, RS (1990). «Вероятностный подход к преобразованию Хафа». Труды Британской конференции по машинному зрению 1990 г. Британская ассоциация машинного зрения. стр. 12.1 – 12.6 . doi :10.5244/c.4.12.
- ^ Йенсен, Йеппе. "Преобразование Хафа для прямых линий" (PDF) . Архивировано из оригинала (PDF) 26 апреля 2012 г. . Получено 16 декабря 2011 г. .
- ^ Фернандес, LAF; Оливейра, MM (2008). «Обнаружение линий в реальном времени с помощью улучшенной схемы голосования преобразования Хафа». Распознавание образов . 41 (1): 299– 314. Bibcode : 2008PatRe..41..299F. doi : 10.1016/j.patcog.2007.04.003. S2CID 5996185.
- ^ Лимбергер, Ф. А.; Оливейра, М. М. (2015). «Обнаружение в реальном времени плоских областей в неорганизованных облаках точек» (PDF) . Распознавание образов . 48 (6): 2043–2053 . Bibcode :2015PatRe..48.2043L. doi :10.1016/j.patcog.2014.12.020. hdl : 10183/97001 .
- ^ Фернандес, LAF; Оливейра, MM (2012). «Общая структура для обнаружения подпространства в неупорядоченных многомерных данных». Распознавание образов . 45 (9): 3566– 3579. Bibcode : 2012PatRe..45.3566F. doi : 10.1016/j.patcog.2012.02.033.
- ^ Баллард, Д. Х. (1981). «Обобщение преобразования Хафа для обнаружения произвольных форм». Распознавание образов . 13 (2): 111– 122. Bibcode :1981PatRe..13..111B. doi :10.1016/0031-3203(81)90009-1. hdl : 1802/13802 .
- ^ Воссельман, Г., Дейкман, С.: «Реконструкция 3D-модели здания по облакам точек и планам местности», Международный архив фотограмметрии, дистанционного зондирования и пространственной информации, том 34, часть 3/W4, 22–24 октября 2001 г., Аннаполис, Массачусетс, США, стр. 37–44.
- ^ Тахир Раббани: «Автоматическая реконструкция промышленных установок – Использование облаков точек и изображений». Архивировано 01.12.2008 в Wayback Machine , страницы 43–44, Publications on Geodesy 62, Делфт, 2006. ISBN 978-90-6132-297-9 .
- ^ Ахтерт, Эльке; Бём, Кристиан; Дэвид, Йорн; Крёгер, Пир; Зимек, Артур (2008). «Глобальная корреляционная кластеризация на основе преобразования Хафа». Статистический анализ и интеллектуальный анализ данных . 1 (3): 111– 127. CiteSeerX 10.1.1.716.6006 . doi :10.1002/sam.10012. S2CID 5111283.
- ^ Тахир Раббани и Франк ван ден Хойвел, «Эффективное преобразование Хафа для автоматического обнаружения цилиндров в облаках точек» в Трудах 11-й ежегодной конференции Высшей школы вычислений и обработки изображений (ASCI '05), Нидерланды, июнь 2005 г.
- ^ Yonghong Xie; Qiang Ji (2002). "Новый эффективный метод обнаружения эллипса". Распознавание объектов, поддерживаемое взаимодействием пользователя для сервисных роботов . Том 2. С. 957–960 . CiteSeerX 10.1.1.1.8792 . doi :10.1109/ICPR.2002.1048464. ISBN 978-0-7695-1695-0. S2CID 9276255.
- ^ "Преобразования изображений - Преобразование Хафа". Homepages.inf.ed.ac.uk . Получено 17 августа 2009 г.
Внешние ссылки
- hough_transform.cpp – код C++ – пример библиотеки CImg ( библиотека с открытым исходным кодом , исходный код C++ , изображения в оттенках серого )
- Интерактивная демонстрация основ преобразования Хафа
- https://web.archive.org/web/20070827233423/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/Hough.html – Java-апплет + источник для изучения преобразования Хафа в форме наклона-пересечения
- https://web.archive.org/web/20070827191440/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/HNF.html – Java Applet + Source для изучения преобразования Хафа в нормальной форме
- http://www.sydlogan.com/deskew.html Архивировано 09.02.2010 на Wayback Machine – Исправление перекоса изображений с помощью преобразования Хафа ( изображения в оттенках серого , исходный код C++ )
- https://web.archive.org/web/20070922090216/http://imaging.gmse.net/articledeskew.html – Исправление перекоса изображений с помощью преобразования Хафа ( исходный код Visual Basic )
- http://www.mitov.com/products/visionlab – бесплатная библиотека для Delphi , C++ и .NET, предназначенная для образовательных целей, содержащая компоненты преобразования Хафа «Линия», «Окружность» и «Отрезок линии».
- Tarsha-Kurdi, F., Landes, T., Grussenmeyer, P., 2007a. Алгоритмы преобразования Хафа и расширенного RANSAC для автоматического обнаружения 3D-плоскостей крыш зданий по данным лидара. Труды ISPRS. Семинар по лазерному сканированию. Эспоо, Финляндия, 12–14 сентября 2007 г.
- Into содержит реализации линейного и кругового преобразования Хафа с открытым исходным кодом на языке C++.
- http://www.vision.ime.usp.br/~edelgado/defesa/code/hough.html Архивировано 05.12.2012 на archive.today Преобразование Хафа для обнаружения эллипса, реализованное на языке C.
- scikit-image Преобразование Хафа для линии, окружности и эллипса, реализованное на Python .
- [1] Преобразование Хафа, основанное на вейвлет-фильтрации, для обнаружения окружности определенного радиуса. ( Код Matlab .)
- Преобразование Хафа для линий с использованием MATLAB Архивировано 13.04.2014 на Wayback Machine
- Преобразование Хафа для окружностей в MATLAB
- KHT – исходный код C++.
- 3DKHT – исходный код C++ и наборы данных.
- Преобразование Хафа по прямой в Python