Формат чисел с плавающей точкой половинной точности
16-битный формат компьютерного числа

В вычислительной технике половинная точность (иногда называемая FP16 или float16 ) — это двоичный формат числа с плавающей точкой , который занимает 16 бит (два байта в современных компьютерах) в памяти компьютера . Он предназначен для хранения значений с плавающей точкой в ​​приложениях, где более высокая точность не является существенной, в частности, в обработке изображений и нейронных сетях .

Почти все современные применения следуют стандарту IEEE 754-2008 , где 16-битный формат с основанием 2 называется binary16 , а показатель степени использует 5 бит. Это может выражать значения в диапазоне ±65 504, при этом минимальное значение выше 1 составляет 1 + 1/1024.

В зависимости от компьютера половинная точность может быть на порядок быстрее двойной точности, например, 550 PFLOPS для половинной точности против 37 PFLOPS для двойной точности у одного облачного провайдера. [1]

Форматы с плавающей точкой
IEEE 754
Другой
Альтернативы
Конусная плавающая точка

История

Существовало несколько более ранних 16-битных форматов с плавающей точкой, включая формат DSP HD61810 компании Hitachi 1982 года (4-битная экспонента и 12-битная мантисса), [2] WIF Томаса Дж. Скотта 1991 года (5 бит экспоненты, 10 бит мантиссы) [3] и процессор 3dfx Voodoo Graphics 1995 года (такой же, как у Hitachi). [4]

ILM искала формат изображения, который мог бы обрабатывать широкий динамический диапазон , но без затрат на жесткий диск и память одинарной или двойной точности с плавающей точкой. [5] Группа программируемого затенения с аппаратным ускорением под руководством Джона Эйри из SGI (Silicon Graphics) использовала тип данных s10e5 в 1997 году как часть усилий по проектированию «bali». Это описано в статье SIGGRAPH 2000 [6] (см. раздел 4.3) и далее задокументировано в патенте США 7518615. [7] Он был популяризирован благодаря использованию в формате изображения OpenEXR с открытым исходным кодом .

Nvidia и Microsoft определили тип данных half в языке Cg , выпущенном в начале 2002 года, и реализовали его в кристалле GeForce FX , выпущенном в конце 2002 года. [8] Однако аппаратная поддержка ускоренных 16-битных операций с плавающей точкой была позднее прекращена Nvidia, прежде чем была вновь введена в мобильном графическом процессоре Tegra X1 в 2015 году.

Расширение F16C в 2012 году позволяет процессорам x86 преобразовывать числа с плавающей точкой половинной точности в числа с плавающей точкой одинарной точности и обратно с помощью машинной инструкции.

Двоичный формат с плавающей точкой половинной точности IEEE 754: binary16

Стандарт IEEE 754 [9] определяет двоичный файл16 как имеющий следующий формат:

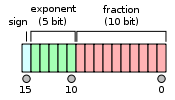
Формат выглядит следующим образом:

Предполагается, что формат имеет неявный ведущий бит со значением 1, если только поле экспоненты не хранится со всеми нулями. Таким образом, в формате памяти появляются только 10 бит мантиссы , но общая точность составляет 11 бит. На языке IEEE 754 имеется 10 бит мантиссы, но имеется 11 бит точности мантиссы (log 10 (2 11 ) ≈ 3,311 десятичных цифр или 4 цифры ± немного меньше 5 единиц в последней позиции ).

Кодирование экспоненты

Двоичная экспонента с плавающей точкой половинной точности кодируется с использованием двоичного представления смещения , при этом нулевое смещение равно 15; также известное как смещение экспоненты в стандарте IEEE 754. [9]

Таким образом, как определено в двоичном представлении смещения, для получения истинной экспоненты необходимо вычесть смещение 15 из сохраненной экспоненты.

Сохраненные показатели 00000 2 и 11111 2 интерпретируются особым образом.

ЭкспонентаЗначащая часть = нольЗначащая часть ≠ нольУравнение
00000 2ноль , −0субнормальные числа(−1) знаковый бит × 2 −14 × 0.значащие биты 2
00001 2 , ..., 11110 2нормализованное значение(−1) знаковый бит × 2 показатель степени−15 × 1.значащие биты 2
11111 2± бесконечностьNaN (тихий, сигнальный)

Минимальное строго положительное (субнормальное) значение равно 2 −24 ≈ 5,96 × 10 −8 . Минимальное положительное нормальное значение равно 2 −14 ≈ 6,10 × 10 −5 . Максимальное представимое значение равно (2−2 −10 ) × 2 15 = 65504.

Примеры половинной точности

Эти примеры даны в битовом представлении значения с плавающей точкой. Это включает бит знака, (смещенную) экспоненту и мантиссу.

ДвоичныйШестигранникЦенитьПримечания
0 00000 000000000000000
0 00000 000000000100012 −14 × (0 + ⁠1/1024⁠ ) ​​≈ 0,000000059604645наименьшее положительное субнормальное число
0 00000 111111111103ff2 −14 × (0 + ⁠1023/1024⁠ ) ​​≈ 0,000060975552наибольшее субнормальное число
0 00001 000000000004002 −14 × (1 + ⁠0/1024⁠ ) ​​≈ 0,00006103515625наименьшее положительное нормальное число
0 01101 010101010135552 −2 × (1 + ⁠341/1024⁠ ) ​​≈ 0,33325195ближайшее значение к 1/3
0 01110 11111111113лучшие друзья2 −1 × (1 + ⁠1023/1024⁠ ) ​​≈ 0,99951172наибольшее число меньше единицы
0 01111 00000000003c002 0 × (1 + ⁠0/1024⁠ ) ​​= 1один
0 01111 00000000013c012 0 × (1 + ⁠1/1024⁠ ) ​​≈ 1,00097656наименьшее число больше единицы
0 11110 11111111117лучшихдрузей2 15 × (1 + ⁠1023/1024⁠ ) ​​= 65504наибольшее нормальное число
0 11111 00000000007c00∞бесконечность
1 00000 00000000008000−0
1 10000 0000000000с000(−1) 1 × 2 1 × (1 + ⁠0/1024⁠ ) ​​= −2
1 11111 0000000000fc00−∞отрицательная бесконечность

По умолчанию 1/3 округляет вниз, как для двойной точности , из-за нечетного количества бит в значащей части. Биты за точкой округления — 0101 ... что меньше 1/2 единицы в последнем разряде .

Ограничения точности

Мин.Максинтервал
02 −132 −24
2 −132 −122 −23
2 −122 −112 −22
2 −112 −102 −21
2 −102 −92 −20
2 −92 −82 −19
2 −82 −72 −18
2 −72 −62 −17
2 −62 −52 −16
2 −52 −42 −15
2 −4⁠1/8⁠2 −14
⁠1/8⁠⁠1/4⁠2 −13
⁠1/4⁠⁠1/2⁠2 −12
⁠1/2⁠12 −11
122 −10
242 −9
482 −8
8162 −7
16322 −6
32642 −5
641282 −4
128256⁠1/8⁠
256512⁠1/4⁠
5121024⁠1/2⁠
102420481
204840962
409681924
8192163848
163843276816
327686552032
65520∞∞

65520 и более крупные числа округляются до бесконечности. Это для округления до четного; другие стратегии округления изменят это ограничение.

ARM альтернатива половинной точности

Процессоры ARM поддерживают (через бит регистра управления с плавающей точкой ) «альтернативный формат половинной точности», который устраняет особый случай для значения показателя степени 31 (11111 2 ). [10] Он почти идентичен формату IEEE, но в нем нет кодировки для бесконечности или NaN; вместо этого показатель степени 31 кодирует нормализованные числа в диапазоне от 65536 до 131008.

Использование половинной точности

Половинная точность используется в нескольких средах компьютерной графики для хранения пикселей, включая MATLAB , OpenEXR , JPEG XR , GIMP , OpenGL , Vulkan , [11] Cg , Direct3D и D3DX . Преимущество перед 8-битными или 16-битными целыми числами заключается в том, что увеличенный динамический диапазон позволяет сохранять больше деталей в светах и ​​тенях изображений и избегать гамма-коррекции. Преимущество перед 32-битной одинарной точностью с плавающей точкой заключается в том, что она требует вдвое меньше памяти и полосы пропускания (за счет точности и диапазона). [5]

Половинная точность может быть полезна для квантования сетки . Данные сетки обычно хранятся с использованием 32-битных чисел одинарной точности с плавающей точкой для вершин, однако в некоторых ситуациях допустимо уменьшить точность до 16-битной половинной точности, что потребует только половины памяти за счет некоторой точности. Квантование сетки также может быть выполнено с 8-битной или 16-битной фиксированной точностью в зависимости от требований. [12]

Аппаратное и программное обеспечение для машинного обучения или нейронных сетей , как правило, использует половинную точность: такие приложения обычно выполняют большой объем вычислений, но не требуют высокого уровня точности. Поскольку оборудование обычно не поддерживает 16-битные числа с плавающей точкой половинной точности, нейронные сети часто используют формат bfloat16 , который представляет собой формат чисел с плавающей точкой одинарной точности, усеченный до 16 бит.

Если оборудование имеет инструкции для вычисления математики с половинной точностью, это часто быстрее, чем одинарная или двойная точность. Если система имеет инструкции SIMD , которые могут обрабатывать несколько чисел с плавающей точкой в ​​одной инструкции, половинная точность может быть в два раза быстрее, работая с вдвое большим количеством чисел одновременно. [13]

Поддержка языков программирования

Zig обеспечивает поддержку половинной точности с его f16типом. [14]

.NET 5 представила числа с плавающей точкой половинной точности в System.Halfстандартном библиотечном типе. [15] [16] По состоянию на январь 2024 года [update]ни один язык .NET ( C# , F# , Visual Basic , C++/CLI и C++/CX ) не имеет литералов (например, в C#, 1.0fhas type System.Singleили 1.0mhas type System.Decimal) или ключевого слова для типа. [17] [18] [19]

Swift представил числа с плавающей точкой половинной точности в Swift 5.3 с типом Float16. [20]

OpenCL также поддерживает числа с плавающей точкой половинной точности с типом данных half в формате хранения половинной точности IEEE 754-2008. [21]

По состоянию на 2024 год [update]Rust работает над добавлением нового f16типа для 16-битных чисел с плавающей точкой половинной точности IEEE. [22]

Julia обеспечивает поддержку чисел с плавающей точкой половинной точности с этим Float16типом. [23]

C++ ввел половинную точность с C++23 вместе с std::float16_tтипом. [24] GCC уже реализует ее поддержку. [25]

Поддержка оборудования

Несколько версий архитектуры ARM поддерживают половинную точность. [26]

Поддержка половинной точности в наборе инструкций x86 указана в расширении набора инструкций F16C , впервые представленном в 2009 году компанией AMD и довольно широко принятом процессорами AMD и Intel к 2012 году. Это было дополнительно расширено до расширения набора инструкций AVX-512_FP16 , реализованного в процессоре Intel Sapphire Rapids . [27]

На RISC-V расширения Zfhи обеспечивают аппаратную поддержку 16-битных чисел с плавающей точкой половинной точности. Расширение является минимальной альтернативой . [28 Zfhmin ]ZfhminZfh

В Power ISA VSX и пока не одобренное расширение SVP64 обеспечивают аппаратную поддержку 16-битных чисел с плавающей точкой половинной точности, начиная с PowerISA v3.1B и более поздних версий. [29] [30]

Поддержка половинной точности в IBM Z является частью функции Neural-network-processing-assist, которую IBM представила с Telum . IBM называет данные с плавающей точкой половинной точности NNP-Data-Type 1 (16 бит).

Смотрите также

Ссылки

  1. ^ "О ABCI - О ABCI | ABCI". abci.ai . Получено 2019-10-06 .
  2. ^ "hitachi :: dataBooks :: HD61810 Цифровой сигнальный процессор Руководство пользователя". Archive.org . Получено 2017-07-14 .
  3. ^ Скотт, Томас Дж. (март 1991 г.). «Математика и информатика в разногласиях по поводу действительных чисел». Труды двадцать второго технического симпозиума SIGCSE по образованию в области компьютерных наук - SIGCSE '91 . Том 23. С.  130–139 . doi : 10.1145/107004.107029 . ISBN 0897913779. S2CID  16648394.
  4. ^ "/home/usr/bk/glide/docs2.3.1/GLIDEPGM.DOC". Gamers.org . Получено 2017-07-14 .
  5. ^ ab "OpenEXR". OpenEXR. Архивировано из оригинала 2013-05-08 . Получено 2017-07-14 .
  6. ^ Марк С. Пирси; Марк Олано; Джон Эйри; П. Джеффри Унгар. «Интерактивное многопроходное программируемое затенение» (PDF) . People.csail.mit.edu . Получено 14 июля 2017 г.
  7. ^ "Патент US7518615 - Система отображения с растеризацией с плавающей точкой и плавающей точкой ... - Google Patents". Google.com . Получено 2017-07-14 .
  8. ^ "vs_2_sw". Документация по инструментарию Cg 3.1 . Nvidia . Получено 17 августа 2016 г.
  9. ^ ab Стандарт IEEE для арифметики с плавающей точкой. IEEE STD 754-2019 (пересмотр IEEE 754-2008). Июль 2019. стр.  1–84 . doi :10.1109/ieeestd.2019.8766229. ISBN 978-1-5044-5924-2.
  10. ^ "Поддержка чисел с плавающей точкой половинной точности". Руководство пользователя компилятора RealView Compilation Tools . 10 декабря 2010 г. Получено 05.05.2015 .
  11. ^ Гаррард, Эндрю. "10.1. 16-битные числа с плавающей точкой". Спецификация формата данных Khronos v1.2 rev 1 . Khronos . Получено 2023-08-05 .
  12. ^ "KHR_mesh_quantization". GitHub . Khronos Group . Получено 2023-07-02 .
  13. ^ Хо, Нхут-Мин; Вонг, Венг-Фай (1 сентября 2017 г.). «Использование арифметики половинной точности в графических процессорах Nvidia» (PDF) . Кафедра компьютерных наук Национального университета Сингапура . Получено 13 июля 2020 г. . Недавно Nvidia представила собственную поддержку чисел с плавающей точкой половинной точности (FP16) в своих графических процессорах Pascal. Это было в основном мотивировано возможностью ускорения ресурсоемких и устойчивых к ошибкам приложений в графических процессорах.
  14. ^ "Floats". ziglang.org . Получено 7 января 2024 г. .
  15. ^ "Half Struct (System)". learn.microsoft.com . Получено 2024-02-01 .
  16. ^ Говиндараджан, Прашант (2020-08-31). "Представляем тип Half!". .NET Blog . Получено 2024-02-01 .
  17. ^ "Числовые типы с плавающей точкой ― Справочник по C#". learn.microsoft.com . 2022-09-29 . Получено 2024-02-01 .
  18. ^ "Литералы ― Справочник по языку F#". learn.microsoft.com . 2022-06-15 . Получено 2024-02-01 .
  19. ^ «Сводка типов данных — Справочник по языку Visual Basic». learn.microsoft.com . 2021-09-15 . Получено 2024-02-01 .
  20. ^ "swift-evolution/proposals/0277-float16.md на главной · apple/swift-evolution". github.com . Получено 13 мая 2024 г. .
  21. ^ "cl_khr_fp16 extension". registry.khronos.org . Получено 31 мая 2024 г. .
  22. ^ Кросс, Трэвис. "Отслеживание проблемы для типов float f16 и f128". GitHub . Получено 2024-07-05 .
  23. ^ "Целые числа и числа с плавающей точкой · Язык Julia". docs.julialang.org . Получено 2024-07-11 .
  24. ^ "P1467R9: Расширенные типы с плавающей точкой и стандартные имена". www.open-std.org . Получено 2024-10-18 .
  25. ^ "106652 – [C++23] P1467 - Расширенные типы с плавающей точкой и стандартные имена". gcc.gnu.org . Получено 2024-10-18 .
  26. ^ "Формат чисел с плавающей точкой половинной точности". Справочное руководство по компилятору ARM armclang версии 6.7 . Разработчик ARM . Получено 13 мая 2022 г. .
  27. ^ Таунер, Дэниел. "Intel® Advanced Vector Extensions 512 - FP16 Instruction Set for Intel® Xeon® Processor Based Products" (PDF) . Программы Intel® Builders . Получено 13 мая 2022 г. .
  28. ^ "RISC-V Instruction Set Manual, Volume I: RISC-V User-Level ISA". Five EmbedDev . Получено 2023-07-02 .
  29. ^ "OPF_PowerISA_v3.1B.pdf". Файлы OpenPOWER . OpenPOWER Foundation . Получено 2023-07-02 .
  30. ^ "ls005.xlen.mdwn". libre-soc.org Git . Получено 2023-07-02 .

Дальнейшее чтение

  • Khronos Vulkan подписал 16-битный формат с плавающей точкой
  • Мини-флоаты (в Обзоре форматов с плавающей точкой )
  • Сайт OpenEXR
  • Константы половинной точности из D3DX
  • Обработка OpenGL половинной точности
  • Быстрые преобразования Half Float
  • Вариант Analog Devices (четырехбитная экспонента)
  • Исходный код C для преобразования между двойной, одинарной и половинной точностью IEEE можно найти здесь.
  • Исходный код Java для преобразования чисел с плавающей точкой половинной точности
  • С плавающей точкой половинной точности для одной из расширенных функций GCC
Retrieved from "https://en.wikipedia.org/w/index.php?title=Half-precision_floating-point_format&oldid=1264780372"