Градиентная оптика
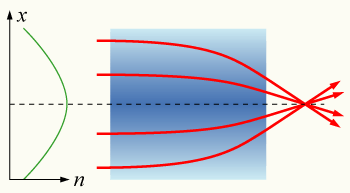
Линза с градиентным показателем преломления с параболическим изменением показателя преломления ( n ) с радиальным расстоянием ( x ). Линза фокусирует свет так же, как и обычная линза.

Градиентная оптика ( GRIN ) — раздел оптики, изучающий оптические эффекты, создаваемые градиентом показателя преломления материала . Такое постепенное изменение может использоваться для создания линз с плоскими поверхностями или линз, не имеющих аберраций, характерных для традиционных сферических линз. Градиентные линзы могут иметь градиент преломления, который является сферическим, осевым или радиальным.

В природе

Хрусталик глаза является наиболее очевидным примером оптики с градиентным показателем преломления в природе. В человеческом глазу показатель преломления хрусталика варьируется от приблизительно 1,406 в центральных слоях до 1,386 в менее плотных слоях хрусталика. [1] Это позволяет глазу получать изображение с хорошим разрешением и низкой аберрацией как на коротких, так и на длинных расстояниях. [2]

Другим примером оптики градиентного показателя преломления в природе является обычный мираж лужи воды, появляющейся на дороге в жаркий день. Лужа на самом деле является изображением неба, по-видимому, расположенного на дороге, поскольку световые лучи преломляются ( отклоняются) от своего обычного прямого пути. Это происходит из-за изменения показателя преломления между горячим, менее плотным воздухом у поверхности дороги и более плотным холодным воздухом над ней. Изменение температуры (и, следовательно, плотности) воздуха вызывает градиент его показателя преломления, заставляя его увеличиваться с высотой. [3] Этот градиент показателя преломления вызывает преломление световых лучей (под небольшим углом к ​​дороге) от неба, изгибая их в глаз наблюдателя, при этом их видимым местоположением является поверхность дороги.

Атмосфера Земли действует как линза GRIN, позволяя наблюдателям видеть солнце в течение нескольких минут после того, как оно фактически скроется за горизонтом, а также наблюдать звезды, находящиеся за горизонтом. [3] Этот эффект также позволяет наблюдать электромагнитные сигналы со спутников после того, как они опустятся за горизонт, как при радиозатменных измерениях.

Приложения

Способность линз GRIN иметь плоские поверхности упрощает монтаж линзы, что делает их полезными там, где необходимо монтировать много очень маленьких линз вместе, например, в фотокопировальных аппаратах и ​​сканерах . [4] Плоская поверхность также позволяет линзе GRIN легко оптически совмещаться с волокном для получения коллимированного выходного сигнала, что делает ее применимой для эндоскопии , а также для визуализации кальция in vivo и оптогенетической стимуляции в мозге. [5]

В приложениях для обработки изображений линзы GRIN в основном используются для уменьшения аберраций. Разработка таких линз включает в себя детальные расчеты аберраций, а также эффективное производство линз. Для линз GRIN использовались различные материалы, включая оптические стекла, пластики, германий , селенид цинка и хлорид натрия . [4]

Некоторые оптические волокна ( волокна с градиентным показателем преломления ) изготавливаются с радиально-изменяющимся профилем показателя преломления; эта конструкция значительно снижает модовую дисперсию многомодового оптического волокна . Радиальное изменение показателя преломления обеспечивает синусоидальное распределение высоты лучей внутри волокна, предотвращая выход лучей из сердцевины . Это отличается от традиционных оптических волокон, которые полагаются на полное внутреннее отражение , тем, что все моды волокон GRIN распространяются с одинаковой скоростью, что обеспечивает более высокую временную полосу пропускания для волокна. [6]

Антибликовые покрытия обычно эффективны для узких диапазонов частоты или угла падения. Градиентные материалы менее ограничены. [7]

Линза с осевым градиентом использовалась для концентрации солнечного света на солнечных элементах, захватывая до 90% падающего света, когда солнце находится не под оптимальным углом. [8]

Производство

Линзы GRIN изготавливаются несколькими способами:

  • Нейтронное облучение – стекло, богатое бором, бомбардируется нейтронами, чтобы вызвать изменение концентрации бора и, следовательно, показателя преломления линзы. [6] [9]
  • Химическое осаждение из паровой фазы – процесс, включающий осаждение различных стекол с различными показателями преломления на поверхность для получения кумулятивного изменения преломления. [6] [10]
  • Частичная полимеризация – органический мономер частично полимеризуется с использованием ультрафиолетового света различной интенсивности, чтобы получить градиент преломления. [6] [11]
  • Ионный обмен – Стекло погружается в жидкий расплав с ионами лития . В результате диффузии ионы натрия в стекле частично обмениваются с ионами лития, причем большая часть обмена происходит на краю. Таким образом, образец приобретает градиентную структуру материала и соответствующий градиент показателя преломления. [6] [12]
  • Ионная набивка – Фазовое разделение определенного стекла приводит к образованию пор, которые впоследствии можно заполнить с помощью различных солей или концентраций солей, чтобы получить различный градиент. [6] [13]
  • Прямая лазерная запись – при поточечном экспонировании предварительно разработанной структуры доза экспонирования варьируется (скорость сканирования, мощность лазера и т.д.). Это соответствует пространственно настраиваемой степени преобразования мономера в полимер, что приводит к разному показателю преломления. Метод применим к микрооптическим элементам свободной формы и многокомпонентной оптике. [14]

История

В 1854 году Дж. К. Максвелл предложил линзу, распределение показателя преломления которой позволило бы четко отображать каждую область пространства. Известная как линза Максвелла «рыбий глаз» , она включает сферическую функцию показателя преломления и, как ожидается, также будет иметь сферическую форму. [15] Однако эта линза непрактична в изготовлении и малополезна, поскольку только точки на поверхности и внутри линзы отображаются четко, а протяженные объекты страдают от экстремальных аберраций. В 1905 году Р. У. Вуд использовал технику погружения, создав желатиновый цилиндр с градиентом показателя преломления, который изменялся симметрично с радиальным расстоянием от оси. Позднее было показано, что дискообразные срезы цилиндра имеют плоские грани с радиальным распределением показателя преломления. Он показал, что, хотя грани линзы были плоскими, они действовали как собирательная и рассеивающая линзы в зависимости от того, уменьшался или увеличивался показатель относительно радиального расстояния. [16] В 1964 году была опубликована посмертная книга Р. К. Люнебурга , в которой он описал линзу , фокусирующую падающие параллельные лучи света в точку на противоположной поверхности линзы. [17] Это также ограничивало применение линзы, поскольку ее было трудно использовать для фокусировки видимого света; однако она была полезна в микроволновых приложениях. Несколько лет спустя было разработано несколько новых методов изготовления линз типа Вуда. С тех пор, по крайней мере, более тонкие линзы GRIN могут обладать удивительно хорошими свойствами изображения, учитывая их очень простую механическую конструкцию, в то время как более толстые линзы GRIN нашли применение, например, в стержнях Selfoc . [18]

Теория

Неоднородная градиентная линза обладает показателем преломления, изменение которого следует функции координат интересующей области в среде. Согласно принципу Ферма , интеграл пути света ( L ), взятый вдоль луча света, соединяющего любые две точки среды , является стационарным относительно своего значения для любой близлежащей кривой, соединяющей две точки. Интеграл пути света задается уравнением н = ф ( х , у , з ) {\displaystyle n=f(x,y,z)}

Л = ∫ С о С н г с {\displaystyle L=\int _{S_{o}}^{S}n\,ds} , где n — показатель преломления, а S — длина дуги кривой. Если используются декартовы координаты , это уравнение модифицируется, чтобы включить изменение длины дуги для сферического градиента в каждое физическое измерение:
Л = ∫ С о С н ( х , у , з ) х ′ 2 + у ′ 2 + з ′ 2 г с {\displaystyle L=\int _{S_{o}}^{S}n(x,y,z){\sqrt {x'^{2}+y'^{2}+z'^{2}}}\,ds}

где штрих соответствует d/d s. [19] Интеграл пути света способен качественно охарактеризовать путь света через линзу, так что линзу можно будет легко воспроизвести в будущем.

Градиент показателя преломления линз GRIN может быть математически смоделирован в соответствии с используемым методом производства. Например, линзы GRIN, изготовленные из материала с радиальным градиентом показателя преломления, такого как SELFOC Microlens , [20] имеют показатель преломления, который изменяется в зависимости от:

н г = н о ( 1 − А г 2 2 ) {\displaystyle n_{r}=n_{o}\left(1-{\frac {Ar^{2}}{2}}\right)} , где n r — показатель преломления на расстоянии r от оптической оси ; n o — расчетный показатель преломления на оптической оси, а A — положительная константа.

Смотрите также

Ссылки

  1. ^ Хехт, Юджин; Зайонц, Альфред (1987). Оптика (2-е изд.). Рединг, Массачусетс: Addison-Wesley. стр. 178. ISBN 978-0201116090. OCLC  13761389.
  2. ^ Ширк Дж. С., Сэндрок М., Скрибнер Д., Флит Э., Строман Р., Баер Э., Хилтнер А. (2006) Обзор NRL , стр. 53–61
  3. ^ ab Tsiboulia, AB (2003). "Линзы с градиентным показателем преломления (GRIN)". В Ronald G. Driggers. Encyclopedia of Optical Engineering , Volume 1. New York, NY: Marcel Dekker. 675-683. ISBN 9780824742508 . 
  4. ^ ab "Руководство по выбору линз с градиентным индексом: типы, характеристики, применение". Engineering360 . Получено 11 июля 2021 г.
  5. ^ "In Vivo Calcium Imaging: The Ultimate Guide". Mightex. 2019. Получено 11 июля 2021 г.
  6. ^ abcdef Мур, Дункан Т. (1980). "Градиентная оптика: обзор". Прикладная оптика . 19 (7): 1035– 1038. doi :10.1364/AO.19.001035.
  7. ^ Чжан, Цзюнь-Чао; Сюн, Ли-Мин; Фан, Мин; Хэ, Хун-Бо (2013). "Широкоугольные и широкополосные градиентные антиотражающие покрытия" (PDF) . Chinese Physics B . 22 (4): 044201. Bibcode :2013ChPhB..22d4201Z. doi :10.1088/1674-1056/22/4/044201 . Получено 13 мая 2016 .
  8. ^ Ирвинг, Майкл (28.06.2022). «Пирамидальные линзы улавливают свет под любым углом, повышая эффективность солнечных элементов». Новый Атлас . Получено 28.06.2022 .
  9. ^ Синай П. (1970). Прикладная оптика . 10, 99-104
  10. ^ Кек Д.Б. и Ольшанский Р., «Оптический волновод с оптимальным градиентом индекса», патент США 3,904,268 (9 сентября 1975 г.).
  11. ^ Мур Р.С., «Пластиковый оптический элемент с градиентом показателя преломления», патент США 3,718,383 (февраль 1973 г.).
  12. ^ Хенслер Дж. Р., «Способ создания градиента показателя преломления в стекле», патент США 3,873,408 (25 марта 1975 г.).
  13. ^ Mohr, RK; Wilder, JA; Macedo, PB; Gupta, PK (1979). "Линзы с градиентным индексом, полученные с помощью процесса молекулярной набивки". Сборник технических докладов, представленных на Тематической встрече по системам оптической визуализации с градиентным индексом, 15-16 мая 1979 г., Рочестер, Нью-Йорк . статья WA1. Вашингтон, округ Колумбия: Оптическое общество Америки. OCLC  489755284.
  14. ^ Зукаускас, Альбертас; Матулатиене, Иева; Пайпулас, Домас; Ниаура, Гединимас; Малинаускас, Мангирдас; Гадонас, Роальдас (2015). «Настройка показателя преломления в 3D-литографии с прямой лазерной записью: на пути к микрооптике GRIN». Обзоры лазеров и фотоники . 9 (6): 706–712 . Бибкод : 2015ЛПРв....9..706З. дои : 10.1002/lpor.201500170.
  15. ^ Максвелл, Джеймс Клерк (1854). «Решения задач: (проб. 3, т. VIII. стр. 188)». Кембриджский и Дублинский математический журнал . 9 : 9–11 .(перепечатано: Нивин, Уильям Дэвидсон, ред. (1890). Научные труды Джеймса Клерка Максвелла. Нью-Йорк: Dover Publications. стр.  76–79 .)
  16. ^ Вуд , Роберт Уильямс (1905). Физическая оптика. Нью-Йорк; Лондон: Macmillan. стр. 71.
  17. ^ Люнебург, Рудольф Карл (1964). Математическая теория оптики . Беркли: Издательство Калифорнийского университета. ISBN 978-0-5203-2826-6. OCLC  1149437946.
  18. ^ Маршан, Э. У. (1976). «Аберрации третьего порядка фотографического Вуда». Журнал оптического общества Америки . 66 (12): 1326– 1330. doi :10.1364/JOSA.66.001326.
  19. ^ Маршан, Эрих В. (1978). Градиентная индексная оптика . Нью-Йорк: Academic Press. ISBN 978-0124707504. OCLC  4497777.
  20. ^ Флорес-Ариас, М.Т.; Бао, К.; Кастело, А.; Перес, М.В.; Гомес-Рейно, К. (15.10.2006). «Кроссоверные соединения в планарной оптике с градиентным показателем преломления». Optics Communications . 266 (2): 490– 494. Bibcode : 2006OptCo.266..490F. doi : 10.1016/j.optcom.2006.05.049. ISSN  0030-4018.
Взято с "https://en.wikipedia.org/w/index.php?title=Градиент-индексная_оптика&oldid=1188825547"