Мыло
В этой статье есть несколько проблем. Помогите улучшить ее или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти сообщения )
|
.jpg/440px-The_top_of_foamy_drink_(Unsplash).jpg)


Пены представляют собой двухфазные материальные системы, в которых газ диспергирован во втором, негазообразном материале, в частности, в которых газовые ячейки заключены в отдельный жидкий или твердый материал. [1] : 6 [2] : 4 [3] Пена «может содержать больше или меньше жидкости [или твердого вещества] в зависимости от обстоятельств», [1] : 6 хотя в случае газожидкостных пен газ занимает большую часть объема. [2] : 4 Слово происходит от средневекового немецкого и в остальном устаревшего veim , в отношении «пенной шапки, образующейся в стакане после того, как пиво было только что налито» (ср. ausgefeimt ). [1] : 1
Теории, касающиеся образования пены, структуры и свойств — в физике и физической химии — несколько различаются между жидкими и твердыми пенами тем, что первые являются динамичными (например, тем, что они «непрерывно деформируются»), в результате диффузии газа между ячейками, стекания жидкости из пены в объемную жидкость и т. д. [1] : 1–2 Теории, касающиеся жидких пен, имеют в качестве прямых аналогов теории, касающиеся эмульсий , [1] : 3 двухфазных материальных систем, в которых одна жидкость заключена в другую. [4]
В большинстве пен объем газа большой, а области газа разделены тонкими пленками жидкости или твердого вещества. [ необходима ссылка ] Примерами пены являются губка для мытья и голова на стакане пива; мыльные пены также известны как мыльная пена . [ не проверено в body ]
Твердые пены могут быть с закрытыми или открытыми ячейками . [ требуется ссылка ] В пене с закрытыми ячейками газ образует дискретные карманы, каждый из которых полностью окружен твердым материалом. В пене с открытыми ячейками газовые карманы соединяются друг с другом. Банная губка является примером пены с открытыми ячейками: [ не проверено в организме ] вода легко протекает через всю структуру, вытесняя воздух. Коврик для сна является примером продукта, состоящего из пены с закрытыми ячейками. [ не проверено в организме ]
Пены являются примерами дисперсных сред . [ не проверено в тексте ] В общем случае присутствует газ, поэтому он делится на пузырьки газа разных размеров (т. е. материал является полидисперсным [ не проверено в тексте ] ) — разделенные жидкими областями, которые могут образовывать пленки, все более тонкие, когда жидкая фаза стекает из системных пленок . [5] [ необходима страница ] Когда основной масштаб мал, т. е. для очень мелкой пены, эту дисперсную среду можно считать типом коллоида . [ не проверено в тексте ]
Пена также может относиться к чему-то, что аналогично пене, например, квантовая пена . [ не проверено в тексте ]
Структура
This section has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Пена во многих случаях представляет собой многомасштабную систему. [ необходима цитата ]

Один масштаб — пузырь: пены материалов обычно неупорядочены и имеют пузырьки разных размеров. [ требуется ссылка ] При больших размерах изучение идеализированных пен тесно связано с математическими проблемами минимальных поверхностей и трехмерных мозаик , также называемых сотами . [ требуется ссылка ] В одном из основных философских источников сообщается, что структура Уэйра –Фелана является наилучшей возможной (оптимальной) элементарной ячейкой идеально упорядоченной пены, [6] [ требуется ссылка ] в то время как законы Плато описывают, как мыльные пленки образуют структуры в пенах. [ требуется ссылка ]
В более низком масштабе, чем пузырь, находится толщина пленки для метастабильных пен, которые можно рассматривать как сеть взаимосвязанных пленок, называемых ламелями . [ требуется ссылка ] В идеале ламели соединяются в триады и расходятся на 120° наружу от точек соединения, [ согласно кому? ] известных как границы плато . [ требуется ссылка ]
Еще более низкий масштаб представляет собой интерфейс жидкость-воздух на поверхности пленки. [ необходима ссылка ] Большую часть времени этот интерфейс стабилизирован слоем амфифильной структуры, часто состоящей из поверхностно-активных веществ , частиц ( эмульсия Пикеринга ) или более сложных ассоциаций. [ необходима ссылка ]
Формирование
This section needs additional citations for verification. (August 2024) |
Для образования пены необходимо несколько условий: наличие механической работы, поверхностно-активных веществ (ПАВ), снижающих поверхностное натяжение , и образование пены быстрее, чем ее разрушение. Для образования пены необходима работа (W) по увеличению площади поверхности (ΔA):
где γ — поверхностное натяжение.
Одним из способов создания пены является дисперсия, когда большое количество газа смешивается с жидкостью. Более специфический метод дисперсии заключается в впрыскивании газа через отверстие в твердом теле в жидкость. Если этот процесс происходит очень медленно, то из отверстия может выходить по одному пузырьку за раз, как показано на рисунке ниже.
Ниже представлена одна из теорий определения времени разделения. Однако, хотя эта теория и дает теоретические данные, соответствующие экспериментальным, отрыв вследствие капиллярности принимается как лучшее объяснение.

Под действием выталкивающей силы пузырек поднимается, что
где - объем пузырька, - ускорение силы тяжести, а ρ 1 - плотность газа, ρ 2 - плотность жидкости. Сила, действующая против силы плавучести, - это сила поверхностного натяжения , которая равна
- ,
где γ — поверхностное натяжение, а — радиус отверстия. По мере того, как в пузырек вдавливается больше воздуха, сила плавучести растет быстрее, чем сила поверхностного натяжения. Таким образом, отрыв происходит, когда сила плавучести достаточно велика, чтобы преодолеть силу поверхностного натяжения.
Кроме того, если рассматривать пузырек как сферу с радиусом и подставить объем в уравнение выше, то разделение происходит в тот момент, когда
Рассматривая это явление с точки зрения капиллярности для пузырька, который формируется очень медленно, можно предположить, что давление внутри везде постоянно. Гидростатическое давление в жидкости обозначается как . Изменение давления на границе раздела газ-жидкость равно капиллярному давлению; следовательно,
где R 1 и R 2 — радиусы кривизны, которые считаются положительными. На ножке пузырька R 3 и R 4 — радиусы кривизны, которые также считаются положительными. Здесь гидростатическое давление в жидкости должно учитывать z, расстояние от вершины до ножки пузырька. Новое гидростатическое давление на ножке пузырька равно p 0 ( ρ 1 − ρ 2 ) z . Гидростатическое давление уравновешивает капиллярное давление, что показано ниже:
Наконец, разница в верхнем и нижнем давлении равна изменению гидростатического давления:
В ножке пузырька форма пузырька почти цилиндрическая; следовательно, либо R 3 , либо R 4 большой, а другой радиус кривизны маленький. По мере того, как ножка пузырька растет в длину, она становится более неустойчивой, поскольку один из радиусов увеличивается, а другой уменьшается. В определенный момент вертикальная длина ножки превышает окружность ножки, и из-за сил плавучести пузырек отделяется, и процесс повторяется. [7]
Стабильность
This section needs additional citations for verification. (August 2024) |
Стабилизация
Стабилизация пены обусловлена силами Ван-дер-Ваальса между молекулами в пене, двойными электрическими слоями, создаваемыми диполярными поверхностно-активными веществами, и эффектом Марангони , который действует как восстанавливающая сила на пластинки.
Эффект Марангони зависит от того, является ли пенящаяся жидкость нечистой. Обычно поверхностно-активные вещества в растворе снижают поверхностное натяжение. Поверхностно-активные вещества также слипаются на поверхности и образуют слой, как показано ниже.
Для возникновения эффекта Марангони пена должна быть вдавлена, как показано на первой картинке. Это вдавливание увеличивает локальную площадь поверхности. Поверхностно-активные вещества имеют большее время диффузии, чем основная часть раствора, поэтому поверхностно-активные вещества менее сконцентрированы в вдавливании.
Кроме того, поверхностное растяжение делает поверхностное натяжение вдавленного пятна больше, чем в окружающей области. Следовательно, поскольку время диффузии для поверхностно-активных веществ велико, эффект Марангони успевает проявиться. Разница в поверхностном натяжении создает градиент, который вызывает поток жидкости из областей с более низким поверхностным натяжением в области с более высоким поверхностным натяжением. На втором рисунке показана пленка в равновесии после того, как эффект Марангони проявился. [8]
Отверждение пены приводит к ее затвердеванию, что делает ее бесконечно стабильной при нормальных условиях. [9]
Дестабилизация
Витольд Рыбчинский и Жак Адамар разработали уравнение для расчета скорости пузырьков, поднимающихся в пене, предполагая, что пузырьки имеют сферическую форму с радиусом .
со скоростью в единицах сантиметров в секунду. ρ 1 и ρ 2 — плотность газа и жидкости соответственно в единицах г/см 3 , а ῃ 1 и ῃ 2 — динамическая вязкость газа и жидкости соответственно в единицах г/см·с, а g — ускорение свободного падения в единицах см/с 2 .
Однако, поскольку плотность и вязкость жидкости намного больше, чем у газа, плотностью и вязкостью газа можно пренебречь, что дает новое уравнение для скорости подъема пузырьков:
Однако эксперименты показали, что более точной моделью возникновения пузырьков является:
Отклонения обусловлены эффектом Марангони и капиллярным давлением, которые влияют на предположение о сферичности пузырьков. Для давления Лапласа изогнутого интерфейса газ-жидкость два главных радиуса кривизны в точке равны R 1 и R 2 . [10] При изогнутом интерфейсе давление в одной фазе больше, чем давление в другой фазе. Капиллярное давление P c определяется уравнением:
- ,
где поверхностное натяжение. Пузырь, показанный ниже, представляет собой газ (фаза 1) в жидкости (фаза 2), точка A обозначает верх пузырька, а точка B обозначает низ пузырька.
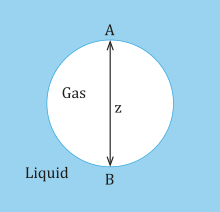
В верхней части пузырька в точке A давление в жидкости предполагается равным p 0, как и в газе. В нижней части пузырька в точке B гидростатическое давление равно:
где ρ 1 и ρ 2 — плотность газа и жидкости соответственно. Разница в гидростатическом давлении в верхней части пузырька равна 0, в то время как разница в гидростатическом давлении в нижней части пузырька через границу раздела равна gz ( ρ 2 − ρ 1 ). Предполагая, что радиусы кривизны в точке A равны и обозначены как R A , а радиусы кривизны в точке B равны и обозначены как R B , тогда разница в капиллярном давлении между точкой A и точкой B равна:
При равновесии разница в капиллярном давлении должна быть уравновешена разницей в гидростатическом давлении. Следовательно,
Так как плотность газа меньше плотности жидкости, левая часть уравнения всегда положительна. Следовательно, обратная величина R A должна быть больше, чем R B . Это означает, что от верха пузырька к низу пузырька радиус кривизны увеличивается. Следовательно, не пренебрегая гравитацией, пузырьки не могут быть сферическими. Кроме того, по мере увеличения z это также вызывает разницу в R A и R B , что означает, что пузырек отклоняется от своей формы тем больше, чем больше он становится. [7]
Дестабилизация пены происходит по нескольким причинам. Во-первых, гравитация вызывает дренаж жидкости к основанию пены, что Рыбчинский и Хадамар включают в свою теорию; однако пена также дестабилизируется из-за осмотического давления , которое вызывает дренаж из ламелей к границам Плато из-за внутренних различий в концентрации в пене, а давление Лапласа вызывает диффузию газа из мелких пузырьков в крупные из-за разницы давлений. Кроме того, пленки могут разрываться под расклинивающим давлением , эти эффекты могут приводить к перестройке структуры пены в масштабах, больших, чем пузырьки, которые могут быть индивидуальными ( процесс T1 ) или коллективными (даже типа «лавины»).
Механические свойства
Жидкие пены
This section needs expansion with: as thorough a treatment as is included in the solid foam subsection. You can help by adding to it. (August 2024) |
Твердые пены
Твердые пены, как с открытыми, так и с закрытыми ячейками, рассматриваются как подкласс ячеистых структур. Они часто имеют более низкую узловую связность [ жаргон ] по сравнению с другими ячеистыми структурами, такими как соты и ферменные решетки, и, таким образом, их механизм разрушения доминирует за счет изгиба элементов. Низкая узловая связность и результирующий механизм разрушения в конечном итоге приводят к их более низкой механической прочности и жесткости по сравнению с сотами и ферменными решетками. [11] [12]
На прочность пенопластов могут влиять плотность, используемый материал и расположение ячеистой структуры (открытая или закрытая, а также изотропия пор). [ требуется ссылка ] Для характеристики механических свойств пенопластов используются кривые зависимости деформации от сжатия для измерения их прочности и способности поглощать энергию, поскольку это важный фактор в технологиях на основе пенопластов. [ требуется ссылка ]
Эластомерная пена
Для эластомерных ячеистых твердых тел, когда пена сжимается, сначала она ведет себя упруго, так как стенки ячеек изгибаются, затем, когда стенки ячеек прогибаются, происходит текучесть и разрушение материала, пока, наконец, стенки ячеек не сомкнутся и материал не разорвется. [13] Это видно на кривой напряжение-деформация как крутой линейный упругий режим, линейный режим с пологим наклоном после текучести (напряжение плато) и экспоненциально возрастающий режим. Жесткость материала можно рассчитать из линейного упругого режима [14] , где модуль для открытоячеистых пен может быть определен уравнением:

где - модуль твердого компонента, - модуль сотовой структуры, - константа, имеющая значение, близкое к единице, - плотность сотовой структуры, - плотность твердого вещества. Модуль упругости для пен с закрытыми ячейками можно описать аналогично:
где единственное отличие — показатель степени в зависимости от плотности. Однако в реальных материалах пена с закрытыми ячейками имеет больше материала на краях ячеек, что делает ее более близкой к уравнению для пен с открытыми ячейками. [15] Соотношение плотности сотовой структуры по сравнению с твердотельной структурой оказывает большое влияние на модуль материала. В целом прочность пены увеличивается с плотностью ячеек и жесткостью материала матрицы.
Энергия деформации
Другим важным свойством, которое можно вывести из кривой деформации напряжения, является энергия, которую пена способна поглотить. Площадь под кривой (указанная как область до быстрого уплотнения при пиковом напряжении) представляет энергию в пене в единицах энергии на единицу объема. Максимальная энергия, запасенная пеной до разрыва, описывается уравнением: [13]
Это уравнение получено из предположения об идеализированной пене с инженерными приближениями из экспериментальных результатов. Большая часть поглощения энергии происходит в области плато напряжения после крутого линейно-упругого режима. [ необходима цитата ]
Зависимость направления
Изотропия ячеистой структуры и поглощение жидкостей также могут оказывать влияние на механические свойства пены. Если присутствует анизотропия, то реакция материалов на напряжение будет направленно-зависимой, и, таким образом, кривая напряжения-деформации, модуль и поглощение энергии будут меняться в зависимости от направления приложенной силы. [ 16] Кроме того, структуры с открытыми ячейками, которые имеют соединенные поры, могут позволять воде или другим жидкостям течь через структуру, что также может влиять на жесткость и способность поглощения энергии. [17]
Приложения
Жидкие пены
Жидкие пены могут использоваться в огнезащитных пенах , таких как те, которые используются при тушении пожаров, особенно нефтяных . [ необходима ссылка ]
Тесто для дрожжевого хлеба традиционно понималось как пена с закрытыми ячейками — дрожжи заставляют хлеб подниматься за счет крошечных пузырьков газа, которые становятся порами хлеба — где клетки не соединяются друг с другом. Разрезание теста высвобождает газ в разрезаемых пузырьках, но газ из остальной части теста не может выйти. [ необходима цитата ] Когда тесту дают подняться слишком сильно, оно становится пеной с открытыми ячейками, в которой газовые карманы соединены; разрезание поверхности теста в этой точке приведет к выходу большого объема газа, и тесто рухнет. [ необходима цитата ] [18] Недавние исследования показали, что структура пор в хлебе на 99% взаимосвязана в одну большую вакуоль, таким образом, пена с закрытыми ячейками влажного теста трансформируется в твердую пену с открытыми ячейками в хлебе. [19] [ необходима неосновная информация ]
Уникальное свойство газожидкостных пен, имеющих очень высокую удельную площадь поверхности, используется в химических процессах пенной флотации и пенного фракционирования . [ необходима ссылка ]
Депопуляция
Пенная депопуляция или вспенивание — это способ массового умерщвления сельскохозяйственных животных путем распыления пены на большой площади, чтобы затруднить дыхание и в конечном итоге вызвать удушье. [20] [21] Обычно его используют, чтобы попытаться остановить распространение болезней. [22]
Твердые пены
This section has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Твердые пены представляют собой класс легких ячеистых инженерных материалов. Эти пены обычно подразделяются на два типа в зависимости от их структуры пор: пены с открытыми ячейками (также известные как сетчатые пены ) и пены с закрытыми ячейками. При достаточно высоком разрешении ячеек любой тип можно рассматривать как непрерывный или «континуальный» материал и называть ячеистыми твердыми телами [23] с предсказуемыми механическими свойствами.

Пены с открытыми ячейками могут использоваться для фильтрации воздуха. Например, было показано, что пена, в которую встроен катализатор, каталитически преобразует формальдегид в безвредные вещества, когда загрязненный формальдегидом воздух проходит через структуру с открытыми ячейками. [24]
Пены с открытыми ячейками содержат поры, которые соединены друг с другом и образуют взаимосвязанную сеть, которая является относительно мягкой. Пены с открытыми ячейками заполняются любым газом, который их окружает. Если они заполнены воздухом, получается относительно хороший изолятор, но если открытые ячейки заполнены водой, изоляционные свойства будут снижены. Недавние исследования сосредоточились на изучении свойств пен с открытыми ячейками как изоляционного материала. Были получены биопены из пшеничного глютена/TEOS , демонстрирующие схожие изоляционные свойства с пенами, полученными из ресурсов на основе нефти. [25] Вспененный каучук является типом пены с открытыми ячейками.

Пенопласты с закрытыми ячейками не имеют взаимосвязанных пор. Пенопласты с закрытыми ячейками обычно имеют более высокую прочность на сжатие из-за своей структуры. Однако пенопласты с закрытыми ячейками также, как правило, более плотные, требуют больше материала и, как следствие, более дороги в производстве. Закрытые ячейки могут быть заполнены специальным газом для обеспечения улучшенной изоляции. Пенопласты с закрытыми ячейками имеют более высокую размерную стабильность, низкие коэффициенты влагопоглощения и более высокую прочность по сравнению с пенопластами с открытыми ячейками. Все типы пенопластов широко используются в качестве основного материала в композитных материалах сэндвич-структуры .
Самое раннее известное инженерное применение ячеистых твердых материалов связано с древесиной, которая в сухом виде представляет собой пену с закрытыми ячейками, состоящую из лигнина, целлюлозы и воздуха. С начала 20-го века стали использоваться различные типы специально изготовленных твердых пен. Низкая плотность этих пен делает их превосходными в качестве теплоизоляторов и флотационных устройств, а их легкость и сжимаемость делают их идеальными в качестве упаковочных материалов и набивок.
Примером использования азодикарбонамида [26] в качестве вспенивающего агента является производство виниловых (ПВХ) и ЭВА-ПЭ пен , где он играет роль в образовании пузырьков воздуха, распадаясь на газ при высокой температуре. [27] [28] [29]
Случайная или «стохастическая» геометрия этих пен делает их также хорошими для поглощения энергии. В конце 20-го века и начале 21-го века новые технологии производства позволили создать геометрию, которая обеспечивает превосходную прочность и жесткость на единицу веса. Эти новые материалы обычно называют сконструированными ячеистыми твердыми телами. [23]
Синтаксическая пена
Интегральная пена для кожи
Интегральная пена для кожи , также известная как пена для самостоятельной кожи , представляет собой тип пены с высокоплотной оболочкой и низкоплотным ядром. Она может быть сформирована в процессе открытой или закрытой формы . В процессе открытой формы два реактивных компонента смешиваются и заливаются в открытую форму. Затем форма закрывается, и смесь расширяется и затвердевает. Примерами изделий, изготовленных с использованием этого процесса, являются подлокотники , детские сиденья , подошвы для обуви и матрасы . Процесс закрытой формы, более известный как реакционное литье под давлением (RIM), впрыскивает смешанные компоненты в закрытую форму под высоким давлением. [30]
Галерея
- Микрофотография закаленной пены (с эффектом памяти)
- Промышленное КТ-сканирование пенопластового шара [ требуется разъяснение ]
- Амортизация из пенополистирола
Масштабы и свойства пены
Смотрите также
- Сэндвич из алюминиевой пены
- Баллистическая пена
- Хаотический пузырь
- Пеногаситель
- Пеностекло
- Металлическая пена
- Нанопена
- Морская пена
- Обратимо собираемые ячеистые композитные материалы
- Пенная вечеринка
- Мягкая материя
Ссылки
- ^ abcde Weaire, D & Hutzler, S (1999). Физика пены. Оксфорд, Англия: Oxford University Press. ISBN 0198510977. Получено 30 августа 2024 г. .
{{cite book}}: CS1 maint: multiple names: authors list (link) Обратите внимание, что этот источник посвящен только жидким пенам. - ^ аб Кантат, я ; Коэн-Аддад, С; Элиас, Ф; Гранер, Ф; Хёлер, Р; Питуа, О; Руйе, Ф., и Сен-Жальм, А. (2013). Пены: структура и динамика. Оксфорд, Англия: Издательство Оксфордского университета. ISBN 978-0199662890. Получено 30 августа 2024 г. .
{{cite book}}: CS1 maint: multiple names: authors list (link) Обратите внимание, что этот источник также фокусируется на жидких пенах. - ^ Общее использование термина, включающее как существительные, так и глагольные формы, является и более узким, и более широким, чем то, которое используется в материаловедении, описанном здесь. В общем использовании оно уже, поскольку чаще всего относится к жидким пенам; оно шире, поскольку включает все виды таких пен и действия по их производству, поэтому, согласно Merriam-Webster , термин относится к «легкой пенистой массе мелких пузырьков, образующихся в жидкости или на ее поверхности или из жидкости», приводя примеры тех, которые производятся «слюноотделением или потоотделением», тех, которые стабильно производятся для тушения пожаров, тех, которые являются продуктом газовых пузырьков, введенных во время производства, а затем дальнейшие общие примеры морской пены, а затем все, что напоминает вышеизложенное. Наконец, общее определение включает действия по производству всего вышеперечисленного. См. «Пена». Merriam-Webster . Архивировано из оригинала 9 декабря 2014 г.
- ^ IUPAC (1997). "Эмульсия". Компендиум химической терминологии (Золотая книга) . Оксфорд: Blackwell Scientific Publications . doi :10.1351/goldbook.E02065. ISBN 978-0-9678550-9-7. Архивировано из оригинала 10 марта 2012 года.
{{cite book}}: CS1 maint: bot: original URL status unknown (link) - ^ Лукассен, Дж. (1981). Лукассен-Рейндерс, Э.Х. (ред.). Анионные ПАВ – Физическая химия действия ПАВ . Нью-Йорк, США: Марсель Деккер.[ нужна страница ]
- ^ Морган, Ф. (2008). «Существование разбиений наименьшего периметра». Philosophical Magazine Letters . 88 ( 9– 10): 647– 650. arXiv : 0711.4228 . Bibcode :2008PMagL..88..647M. doi :10.1080/09500830801992849.
- ^ ab Bikerman, JJ "Формирование и структура" в Foams New York, Springer-Verlag, 1973. ch 2. sec 24–25
- ^ "The Foam" (PDF) . IHC News . Январь 2009. Архивировано из оригинала (PDF) 12 декабря 2013 года . Получено 9 декабря 2013 года .
- ^ Стивенсон, Пол (3 января 2012 г.). Технология пенопласта: основы и применение. John Wiley & Sons. ISBN 9781119961093.
- ^ Уилсон, А. Дж., «Принципы образования и стабильности пены». Пены: физика, химия и структура . Нью-Йорк, Springer-Verlag, 1989, гл. 1
- ^ Queheillat, Дуглас Т.; Уодли, Гайдн Н.Г. (январь 2005 г.). «Ячеистые металлические решетки с полыми фермами». Акта Материалия . 53 (2): 303–313 . Бибкод : 2005AcMat..53..303Q. doi :10.1016/j.actamat.2004.09.024.
- ^ Куистра, Грегори В.; Дешпанде, Викрам С.; Уодли, Гайдн Н.Г. (август 2004 г.). «Поведение при сжатии упрочняемых возрастом ферменных конструкций тетраэдрической решетки из алюминия». Акта Материалия . 52 (14): 4229–4237 . Бибкод : 2004AcMat..52.4229K. doi :10.1016/j.actamat.2004.05.039. S2CID 13958881.
- ^ ab Courtney, Thomas H. (2005). Механическое поведение материалов . Waveland Press, Inc. стр. 686–713 . ISBN 1-57766-425-6.
- ^ М. Лю и др. Многомасштабное моделирование эффективных упругих свойств пористых материалов, заполненных жидкостью Международный журнал твердых тел и структур (2019) 162, 36-44
- ^ Эшби, МФ (1983). «Механические свойства ячеистых твердых тел». Metallurgical Transactions . 14A (9): 1755– 1769. Bibcode : 1983MTA....14.1755A. doi : 10.1007/bf02645546. S2CID 135765088.
- ^ Ли, Пей; Го, YB; Шим, VPW (2020). «Чувствительная к скорости конститутивная модель для анизотропных ячеистых материалов — применение к поперечно-изотропной полиуретановой пене». International Journal of Solids and Structures . 206 : 43–58 . doi :10.1016/j.ijsolstr.2020.08.007. S2CID 225310568 – через Elsevier.
- ^ Ю, YJ; Хирон, K.; Уилсон, TS; Мейтленд, DJ (2011). "Влияние поглощения влаги на физические свойства полиуретановых полимерных пен с эффектом памяти формы". Smart Materials and Structures . 20 (8). Bibcode : 2011SMaS ... 20h5010Y. doi : 10.1088/0964-1726/20/8/085010. PMC 3176498. PMID 21949469.
- ^ Открытую структуру переподнявшегося теста легко наблюдать: вместо того, чтобы состоять из отдельных пузырьков газа, тесто состоит из газового пространства, заполненного нитями мучно-водной пасты. [ оригинальное исследование? ] [ необходима цитата ]
- ^ Ван, Шуо; Остин, Питер; Чакрабати-Белл, Сумана (2011). «Это лабиринт: пористая структура хлебных крошек». Журнал зерновых наук . 54 (2): 203–210 . doi :10.1016/j.jcs.2011.05.004.
- ^ «Новое оружие в войне с птичьим гриппом: крошечные пузырьки». NBC News . 10 июня 2007 г. Получено 21 января 2024 г.
- ^ Бенсон, Э.Р.; Альфин, Р.Л.; Доусон, М.Д.; Мэлоун, Г.В. (май 2009 г.). «Использование пены на водной основе для депопуляции уток и других видов». Poultry Science . 88 (5): 904–910 . doi :10.3382/ps.2008-00268. PMID 19359675.
- ^ Болотникова, Марина (8 марта 2022 г.). «„Они готовят их заживо“: призывы запретить „жестокие“ методы убийства на фермах США». The Guardian . ISSN 0261-3077 . Получено 21 января 2024 г. .
- ^ ab Gibson, Ashby (1999). Cellular Solids: Structure and Properties . Кембридж, Великобритания: Cambridge University Press. ISBN 9781316025420.
- ^ Кэрролл, Грегори Т.; Киршман, Дэвид Л. (23 января 2023 г.). «Устройство каталитической фильтрации хирургического дыма снижает уровень формальдегида в имитируемой операционной среде». ACS Chemical Health & Safety . 30 (1): 21– 28. doi :10.1021/acs.chas.2c00071. ISSN 1871-5532. S2CID 255047115.
- ^ Wu, Qiong; Andersson, Richard L.; Holgate, Tim; Johansson, Eva; Gedde, Ulf W.; Olsson, Richard T.; Hedenqvist, Mikael S. (2014). «Высокопористая огнестойкая и устойчивая биопена на основе пшеничного глютена и полимеризованного на месте диоксида кремния». Journal of Materials Chemistry A. 2 ( 48). 20996–21009. doi : 10.1039/C4TA04787G .
- ^ Рейес-Лабарта, JA; Марцилла, A. (2008). «Кинетическое исследование разложений, вовлеченных в термическую деградацию коммерческого азодикарбонамида». Журнал прикладной полимерной науки . 107 (1): 339– 346. doi :10.1002/app.26922. hdl : 10045/24682 .
- ^ Рейес-Лабарта, JA; Марцилла, A. (2012). «Термическая обработка и деградация сшитых пен этиленвинилацетата-полиэтилена-азодикарбонамида-ZnO. Полное кинетическое моделирование и анализ». Industrial & Engineering Chemistry Research . 51 (28): 9515– 9530. doi :10.1021/ie3006935.
- ^ Рейес-Лабарта, JA; Марцилла, A. (2008). «Анализ дифференциальной сканирующей калориметрии термической обработки тройных смесей этиленвинилацетата, полиэтилена и азодикарбонамида». Журнал прикладной полимерной науки . 110 (5): 3217– 3224. doi :10.1002/app.28802. hdl : 10045/13312 .
- ^ Рейес-Лабарта, JA; Олайя, MM; Марцилла, A. (2006). «DSC-исследование переходов, вовлеченных в термическую обработку вспениваемых смесей сополимера ПЭ и ЭВА с азодикарбонамидом». Журнал прикладной полимерной науки . 102 (3): 2015–2025 . doi :10.1002/app.23969. hdl : 10045/24680 .
- ^ Ашида, Канеёши (2006). Полиуретан и родственные пены: химия и технология. CRC Press. С. 79–81 . ISBN 978-1-58716-159-9. Архивировано из оригинала 17 февраля 2017 года.
Дальнейшее чтение
- Weaire, D & Hutzler, S (1999). Физика пены. Оксфорд, Англия: Oxford University Press. ISBN 0198510977. Получено 30 августа 2024 г. .
{{cite book}}: CS1 maint: multiple names: authors list (link)Современный трактат, посвященный почти исключительно жидким пенам. - Гибсон, Л. Дж. и Эшби, М. Ф. (1997). Клеточные твердые тела: структура и свойства. Cambridge Solid State Science. Кембридж, Англия: Cambridge University Press. ISBN 0521499119. Получено 30 августа 2024 г. .
{{cite book}}: CS1 maint: multiple names: authors list (link)Трактат, названный классикой Уайром и Хатцлером (1999), о твердых пенах и о причинах, по которым они ограничивают свое внимание жидкими пенами. - Кантат, я ; Коэн-Аддад, С; Элиас, Ф; Гранер, Ф; Хёлер, Р; Питуа, О; Руйе, Ф., и Сен-Жальм, А. (2013). Пены: структура и динамика. Оксфорд, Англия: Издательство Оксфордского университета. ISBN 978-0199662890. Получено 30 августа 2024 г. .
{{cite book}}: CS1 maint: multiple names: authors list (link) Обратите внимание, что этот источник также фокусируется на жидких пенах. - Томас Хипке, Гюнтер Ланге, Рене Посс: Taschenbuch für Aluminiumschäume. Aluminium-Verlag, Дюссельдорф, 2007 г., ISBN 978-3-87017-285-5 .
- Ханнелоре Диттмар-Ильген: Metalle lernen schwimmen. В: Dies.: Wie der Kork-Krümel ans Weinglas kommt. Хирцель, Штутгарт 2006, ISBN 978-3-7776-1440-3 , S. 74.
Внешние ссылки
- Эндрю М. Крайник, Дуглас А. Рейнельт, Франк ван Свол Структура случайной монодисперсной пены
- Мориарти, Филип (2010). «Физика пены». Шестьдесят символов . Брэди Харан для Ноттингемского университета .


























![[icon]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/44px-Wiki_letter_w_cropped.svg.png)







![{\displaystyle {\frac {W_{max}}{E_{s}}}=0,05\left({\frac {\rho ^{*}}{\rho _{s}}}\right)^{2}\left[0,975-1,4\left({\frac {\rho ^{*}}{\rho _{s}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/037551eb3a9f7c6a5595941b2b2336f792664d2f)

![Уплотнение для проникновения силиконовой пены [требуется разъяснение]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/f6/Silikonschaum_riesenblase_verfuellungsversuch.jpg/440px-Silikonschaum_riesenblase_verfuellungsversuch.jpg)
![Промышленное КТ-сканирование пенопластового шара [требуется разъяснение]](http://upload.wikimedia.org/wikipedia/commons/thumb/9/9d/Foam_ball.png/120px-Foam_ball.png)

![Вспененный алюминий [требуется разъяснение]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/fc/Aluminium_foam.jpg/440px-Aluminium_foam.jpg)

