Статистика Ферми-Дирака

Статистическая механика
Термодинамика Кинетическая теория
Статистика частиц Теорема о спиновой статистике Неразличимые частицы Максвелл–Больцман Бозе–Эйнштейн Ферми–Дирак Парастатистика Статистика Anyonic Статистика кос
Термодинамические ансамбли NVE Микроканонический NVT Канонический µVT Гранд канонический NPH Изоэнтальпийно-изобарический NPT Изотермический–изобарический
Модели Дебай Эйнштейн Изинг Поттс
Потенциалы Внутренняя энергия Энтальпия Свободная энергия Гельмгольца Свободная энергия Гиббса Большой потенциал / Свободная энергия Ландау
Ученые Максвелл Больцман Гельмгольц Бозе Гиббс Эйнштейн Дирак Эренфест фон Нейман Толман Дебай Ферми Синг Изинг Ландо
в т е

Статистика Ферми–Дирака — это тип квантовой статистики , которая применяется к физике системы , состоящей из множества невзаимодействующих, идентичных частиц , которые подчиняются принципу исключения Паули . Результатом является распределение Ферми–Дирака частиц по энергетическим состояниям . Оно названо в честь Энрико Ферми и Поля Дирака , каждый из которых вывел это распределение независимо в 1926 году. ^{[1] [2]} Статистика Ферми–Дирака является частью области статистической механики и использует принципы квантовой механики .

Статистика Ферми–Дирака применяется к идентичным и неразличимым частицам с полуцелым спином (1/2, 3/2 и т. д.), называемым фермионами , в термодинамическом равновесии . В случае пренебрежимо малого взаимодействия между частицами система может быть описана в терминах одночастичных энергетических состояний . Результатом является распределение Ферми–Дирака частиц по этим состояниям, где никакие две частицы не могут занимать одно и то же состояние, что оказывает значительное влияние на свойства системы. Статистика Ферми–Дирака чаще всего применяется к электронам , типу фермионов со спином 1/2 .

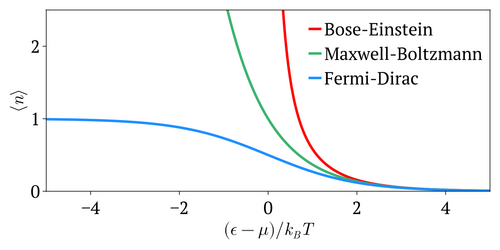
Аналогом статистики Ферми–Дирака является статистика Бозе–Эйнштейна , которая применяется к идентичным и неразличимым частицам с целым спином (0, 1, 2 и т. д.), называемым бозонами . В классической физике статистика Максвелла–Больцмана используется для описания частиц, которые идентичны и рассматриваются как различимые. Как для статистики Бозе–Эйнштейна, так и для статистики Максвелла–Больцмана, в отличие от статистики Ферми–Дирака, более одной частицы могут занимать одно и то же состояние.

До введения статистики Ферми-Дирака в 1926 году понимание некоторых аспектов поведения электронов было затруднено из-за, казалось бы, противоречивых явлений. Например, электронная теплоемкость металла при комнатной температуре , казалось, исходила от в 100 раз меньшего количества электронов , чем было в электрическом токе . ^[3] Также было трудно понять, почему токи эмиссии, генерируемые приложением сильных электрических полей к металлам при комнатной температуре, почти не зависели от температуры.

Трудность, с которой столкнулась модель Друде , электронная теория металлов того времени, была вызвана тем, что считалось, что все электроны (согласно классической статистической теории) эквивалентны. Другими словами, считалось, что каждый электрон вносит в удельную теплоту величину порядка постоянной Больцмана  k _B . Эта проблема оставалась нерешенной до развития статистики Ферми–Дирака.

Статистика Ферми–Дирака была впервые опубликована в 1926 году Энрико Ферми ^[1] и Полем Дираком . ^[2] По словам Макса Борна , Паскуаль Джордан разработал в 1925 году ту же самую статистику, которую он назвал статистикой Паули , но она не была опубликована своевременно. ^{[4] [5] [6]} По словам Дирака, она была впервые изучена Ферми, и Дирак назвал ее «статистикой Ферми», а соответствующие частицы «фермионами». ^[7]

Статистика Ферми–Дирака была применена в 1926 году Ральфом Фаулером для описания коллапса звезды в белый карлик . ^[8] В 1927 году Арнольд Зоммерфельд применил ее к электронам в металлах и разработал модель свободных электронов , ^[9] а в 1928 году Фаулер и Лотар Нордхейм применили ее к полевой электронной эмиссии из металлов. ^[10] Статистика Ферми–Дирака продолжает оставаться важной частью физики.

Для системы идентичных фермионов в термодинамическом равновесии среднее число фермионов в одночастичном состоянии i задается распределением Ферми–Дирака (Ф–Д) : ^{[11] [nb 1]}

где k _B — постоянная Больцмана , T — абсолютная температура , ε _i — энергия одночастичного состояния i , а μ — полный химический потенциал . Распределение нормируется условием

${\displaystyle \sum _{i}{\bar {n}}_{i}=N}$

, который может быть использован для выражения в , который может принимать как положительное, так и отрицательное значение. ^[12]${\displaystyle \mu =\mu (T,N)}$${\displaystyle \mu }$

При нулевой абсолютной температуре μ равно энергии Ферми плюс потенциальная энергия на фермион, при условии, что он находится в окрестности положительной спектральной плотности. В случае спектральной щели, например, для электронов в полупроводнике, точка симметрии μ обычно называется уровнем Ферми или — для электронов — электрохимическим потенциалом и будет расположена в середине щели. ^{[13] [14]}

Распределение Ферми-Дирака справедливо только в том случае, если число фермионов в системе достаточно велико, так что добавление еще одного фермиона в систему оказывает незначительное влияние на μ . ^[15] Поскольку распределение Ферми-Дирака было получено с использованием принципа исключения Паули , который позволяет максимум одному фермиону занимать каждое возможное состояние, результатом является то, что . ^{[nb 2]}${\displaystyle 0<{\bar {n}}_{i}<1}$

• Распределение Ферми-Дирака
• 
  Зависимость от энергии. Более постепенная при более высоких T . когда . Не показано, что уменьшается при более высоких T . ^[16]${\displaystyle {\bar {n}}=0.5}$${\displaystyle \varepsilon =\mu }$${\displaystyle \mu }$
• 
  Температурная зависимость для .${\displaystyle \varepsilon >\mu }$

Дисперсию числа частиц в состоянии i можно рассчитать из приведенного выше выражения для : ^[17] [ ^18]${\displaystyle {\bar {n}}_{i}}$

${\displaystyle V(n_{i})=k_{\text{B}}T{\frac {\partial }{\partial \mu }}{\bar {n}}_{i}={\bar {n}}_{i}(1-{\bar {n}}_{i}).}$

Из распределения Ферми-Дирака частиц по состояниям можно найти распределение частиц по энергии. ^{[nb 3]} Среднее число фермионов с энергией можно найти, умножив распределение Ферми-Дирака на вырождение (т.е. число состояний с энергией ), ^[19]${\displaystyle \varepsilon _{i}}$${\displaystyle {\bar {n}}_{i}}$ ${\displaystyle g_{i}}$${\displaystyle \varepsilon _{i}}$

${\displaystyle {\begin{aligned}{\bar {n}}(\varepsilon _{i})&=g_{i}{\bar {n}}_{i}\\&={\frac {g_{i}}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}+1}}.\end{aligned}}}$

Когда , возможно, что , поскольку существует более одного состояния, которое могут занимать фермионы с одинаковой энергией .${\displaystyle g_{i}\geq 2}$${\displaystyle {\bar {n}}(\varepsilon _{i})>1}$${\displaystyle \varepsilon _{i}}$

Когда квазиконтинуум энергий имеет связанную с ним плотность состояний (т.е. число состояний на единицу диапазона энергии на единицу объема ^[20] ), среднее число фермионов на единицу диапазона энергии на единицу объема равно${\displaystyle \varepsilon }$ ${\displaystyle g(\varepsilon )}$

${\displaystyle {\bar {\mathcal {N}}}(\varepsilon )=g(\varepsilon )F(\varepsilon ),}$

где называется функцией Ферми и является той же функцией , которая используется для распределения Ферми–Дирака : ^[21]${\displaystyle F(\varepsilon )}$${\displaystyle {\bar {n}}_{i}}$

${\displaystyle F(\varepsilon )={\frac {1}{e^{(\varepsilon -\mu )/k_{\text{B}}T}+1}},}$

так что

${\displaystyle {\bar {\mathcal {N}}}(\varepsilon )={\frac {g(\varepsilon )}{e^{(\varepsilon -\mu )/k_{\text{B}}T}+1}}.}$

Распределение Ферми–Дирака приближается к распределению Максвелла–Больцмана в пределе высокой температуры и низкой плотности частиц, без необходимости каких-либо специальных предположений:

• В пределе низкой плотности частиц, , следовательно, или, что эквивалентно , . В этом случае, , что является результатом статистики Максвелла-Больцмана.${\displaystyle {\bar {n}}_{i}={\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\rm {B}}T}+1}}\ll 1}$${\displaystyle e^{(\varepsilon _{i}-\mu )/k_{\rm {B}}T}+1\gg 1}$${\displaystyle e^{(\varepsilon _{i}-\mu )/k_{\rm {B}}T}\gg 1}$${\displaystyle {\bar {n}}_{i}\approx {\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\rm {B}}T}}}={\frac {N}{Z}}e^{-\varepsilon _{i}/k_{\rm {B}}T}}$
• В пределе высокой температуры частицы распределены по большому диапазону значений энергии, поэтому заселенность каждого состояния (особенно высокоэнергетических с ) снова очень мала, . Это снова сводится к статистике Максвелла-Больцмана.${\displaystyle \varepsilon _{i}-\mu \gg k_{\rm {B}}T}$${\displaystyle {\bar {n}}_{i}={\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\rm {B}}T}+1}}\ll 1}$

Классический режим, в котором статистика Максвелла-Больцмана может быть использована в качестве приближения к статистике Ферми-Дирака, находится путем рассмотрения ситуации, которая далека от предела, налагаемого принципом неопределенности Гейзенберга для положения и импульса частицы . Например, в физике полупроводников, когда плотность состояний зоны проводимости намного выше концентрации легирования, энергетический зазор между зоной проводимости и уровнем Ферми может быть рассчитан с использованием статистики Максвелла-Больцмана. В противном случае, если концентрация легирования не является пренебрежимо малой по сравнению с плотностью состояний зоны проводимости, вместо этого для точного расчета следует использовать распределение Ферми-Дирака. Затем можно показать, что классическая ситуация преобладает, когда концентрация частиц соответствует среднему межчастичному расстоянию , которое намного больше средней длины волны де Бройля частиц: ^[22]${\displaystyle {\bar {R}}}$ ${\displaystyle {\bar {\lambda }}}$

${\displaystyle {\bar {R}}\gg {\bar {\lambda }}\approx {\frac {h}{\sqrt {3mk_{\rm {B}}T}}},}$

где h — постоянная Планка , а m — масса частицы .

Для случая электронов проводимости в типичном металле при T = 300  K (т.е. примерно комнатной температуре) система далека от классического режима, поскольку . Это связано с малой массой электрона и высокой концентрацией (т.е. малым ) электронов проводимости в металле. Таким образом, для электронов проводимости в типичном металле необходима статистика Ферми–Дирака. ^[22]${\displaystyle {\bar {R}}\approx {\bar {\lambda }}/25}$${\displaystyle {\bar {R}}}$

Другим примером системы, которая не находится в классическом режиме, является система, состоящая из электронов звезды, которая коллапсировала в белый карлик. Хотя температура белого карлика высока (обычно T =10 000  К на его поверхности ^[23] ), его высокая концентрация электронов и малая масса каждого электрона исключают возможность использования классического приближения, и снова требуется статистика Ферми-Дирака. ^[8]

Распределение Ферми–Дирака, которое применимо только к квантовой системе невзаимодействующих фермионов, легко выводится из большого канонического ансамбля . ^[24] В этом ансамбле система способна обмениваться энергией и обмениваться частицами с резервуаром (температура T и химический потенциал μ фиксируются резервуаром).

Благодаря невзаимодействующему качеству каждый доступный одночастичный уровень (с уровнем энергии ϵ ) образует отдельную термодинамическую систему в контакте с резервуаром. Другими словами, каждый одночастичный уровень является отдельным, крошечным большим каноническим ансамблем. Согласно принципу исключения Паули, существует только два возможных микросостояния для одночастичного уровня: ни одной частицы (энергия E = 0) или одна частица (энергия E = ε ). Таким образом, результирующая функция распределения для этого одночастичного уровня имеет всего два члена:

${\displaystyle {\begin{aligned}{\mathcal {Z}}&=\exp {\big (}0(\mu -\varepsilon )/k_{\rm {B}}T{\big )}+\exp {\big (}1(\mu -\varepsilon )/k_{\rm {B}}T{\big )}\\&=1+\exp {\big (}(\mu -\varepsilon )/k_{\rm {B}}T{\big )},\end{aligned}}}$

и среднее число частиц для этого одночастичного уровня подсостояния определяется как

${\displaystyle \langle N\rangle =k_{\rm {B}}T{\frac {1}{\mathcal {Z}}}\left({\frac {\partial {\mathcal {Z}}}{\partial \mu }}\right)_{V,T}={\frac {1}{\exp {\big (}(\varepsilon -\mu )/k_{\rm {B}}T{\big )}+1}}.}$

Этот результат применим к каждому одночастичному уровню и, таким образом, дает распределение Ферми–Дирака для всего состояния системы. ^[24]

Также можно вывести дисперсию числа частиц (из-за тепловых флуктуаций ) (число частиц имеет простое распределение Бернулли ):

${\displaystyle {\big \langle }(\Delta N)^{2}{\big \rangle }=k_{\rm {B}}T\left({\frac {d\langle N\rangle }{d\mu }}\right)_{V,T}=\langle N\rangle {\big (}1-\langle N\rangle {\big )}.}$

Эта величина важна в явлениях переноса, таких как соотношения Мотта для электропроводности и коэффициента термоЭДС для электронного газа ^[25] , где способность энергетического уровня вносить вклад в явления переноса пропорциональна .${\displaystyle {\big \langle }(\Delta N)^{2}{\big \rangle }}$

Также возможно вывести статистику Ферми–Дирака в каноническом ансамбле . Рассмотрим многочастичную систему, состоящую из N идентичных фермионов, которые имеют пренебрежимо малое взаимодействие друг с другом и находятся в тепловом равновесии. ^[15] Поскольку взаимодействие между фермионами пренебрежимо мало, энергия состояния многочастичной системы может быть выражена как сумма одночастичных энергий:${\displaystyle E_{R}}$${\displaystyle R}$

${\displaystyle E_{R}=\sum _{r}n_{r}\varepsilon _{r},}$

где называется числом заполнения и представляет собой число частиц в одночастичном состоянии с энергией . Суммирование ведется по всем возможным одночастичным состояниям .${\displaystyle n_{r}}$${\displaystyle r}$${\displaystyle \varepsilon _{r}}$${\displaystyle r}$

Вероятность того, что многочастичная система находится в состоянии, определяется нормализованным каноническим распределением : ^[26]${\displaystyle R}$

${\displaystyle P_{R}={\frac {e^{-\beta E_{R}}}{\displaystyle \sum _{R'}e^{-\beta E_{R'}}}},}$

где , называется фактором Больцмана , а суммирование ведется по всем возможным состояниям многочастичной системы. Среднее значение для числа заполнения равно ^[26]${\displaystyle \beta =1/k_{\text{B}}T}$${\displaystyle e^{-\beta E_{R}}}$${\displaystyle R'}$${\displaystyle n_{i}}$

${\displaystyle {\bar {n}}_{i}=\sum _{R}n_{i}P_{R}.}$

Обратите внимание, что состояние многочастичной системы можно определить с помощью заполнения частицами одночастичных состояний, т.е. указав так, что${\displaystyle R}$${\displaystyle n_{1},n_{2},\ldots ,}$

${\displaystyle P_{R}=P_{n_{1},n_{2},\ldots }={\frac {e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+\cdots )}}{\displaystyle \sum _{{n_{1}}',{n_{2}}',\ldots }e^{-\beta (n_{1}'\varepsilon _{1}+n_{2}'\varepsilon _{2}+\cdots )}}},}$

и уравнение для становится${\displaystyle {\bar {n}}_{i}}$

${\displaystyle {\begin{aligned}{\bar {n}}_{i}&=\sum _{n_{1},n_{2},\dots }n_{i}P_{n_{1},n_{2},\dots }\\&={\frac {\displaystyle \sum _{n_{1},n_{2},\dots }n_{i}e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+\cdots +n_{i}\varepsilon _{i}+\cdots )}}{\displaystyle \sum _{n_{1},n_{2},\dots }e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+\cdots +n_{i}\varepsilon _{i}+\cdots )}}},\end{aligned}}}$

где суммирование ведется по всем комбинациям значений, которые подчиняются принципу исключения Паули, и = 0 или для каждого . Кроме того, каждая комбинация значений удовлетворяет ограничению, что общее число частиц равно :${\displaystyle n_{1},n_{2},\ldots }$${\displaystyle n_{r}=0}$${\displaystyle 1}$${\displaystyle r}$${\displaystyle n_{1},n_{2},\ldots }$${\displaystyle N}$

${\displaystyle \sum _{r}n_{r}=N.}$

Переставляя суммы,

${\displaystyle {\bar {n}}_{i}={\frac {\displaystyle \sum _{n_{i}=0}^{1}n_{i}e^{-\beta (n_{i}\varepsilon _{i})}\sideset {}{^{(i)}}\sum _{n_{1},n_{2},\dots }e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+\cdots )}}{\displaystyle \sum _{n_{i}=0}^{1}e^{-\beta (n_{i}\varepsilon _{i})}\sideset {}{^{(i)}}\sum _{n_{1},n_{2},\dots }e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+\cdots )}}},}$

где верхний индекс на знаке суммы указывает, что сумма не закончена и подчиняется ограничению, что общее число частиц, связанных с суммированием, равно . Обратите внимание, что все еще зависит от через ограничение, так как в одном случае и оценивается с помощью в то время как в другом случае и оценивается с помощью Чтобы упростить обозначения и четко указать, что все еще зависит от через определить${\displaystyle (i)}$${\displaystyle n_{i}}$${\displaystyle N_{i}=N-n_{i}}$${\displaystyle \textstyle \sum ^{(i)}}$${\displaystyle n_{i}}$${\displaystyle N_{i}}$${\displaystyle n_{i}=0}$${\displaystyle \textstyle \sum ^{(i)}}$${\displaystyle N_{i}=N,}$${\displaystyle n_{i}=1,}$${\displaystyle \textstyle \sum ^{(i)}}$${\displaystyle N_{i}=N-1.}$${\displaystyle \textstyle \sum ^{(i)}}$${\displaystyle n_{i}}$${\displaystyle N-n_{i},}$

${\displaystyle Z_{i}(N-n_{i})\equiv \sideset {}{^{(i)}}\sum _{n_{1},n_{2},\ldots }e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+\cdots )},}$

так что предыдущее выражение для можно переписать и оценить в терминах :${\displaystyle {\bar {n}}_{i}}$${\displaystyle Z_{i}}$

${\displaystyle {\begin{aligned}{\bar {n}}_{i}&={\frac {\displaystyle \sum _{n_{i}=0}^{1}n_{i}e^{-\beta (n_{i}\varepsilon _{i})}\,Z_{i}(N-n_{i})}{\displaystyle \sum _{n_{i}=0}^{1}e^{-\beta (n_{i}\varepsilon _{i})}\,Z_{i}(N-n_{i})}}\\&={\frac {0+e^{-\beta \varepsilon _{i}}\,Z_{i}(N-1)}{Z_{i}(N)+e^{-\beta \varepsilon _{i}}\,Z_{i}(N-1)}}\\&={\frac {1}{[Z_{i}(N)/Z_{i}(N-1)]\,e^{\beta \varepsilon _{i}}+1}}.\end{aligned}}}$

Для нахождения выражения для замены будет использовано следующее приближение ^[27] :${\displaystyle Z_{i}(N)/Z_{i}(N-1)}$

${\displaystyle {\begin{aligned}\ln Z_{i}(N-1)&\simeq \ln Z_{i}(N)-{\frac {\partial \ln Z_{i}(N)}{\partial N}}\\&=\ln Z_{i}(N)-\alpha _{i},\end{aligned}}}$

где${\displaystyle \alpha _{i}\equiv {\frac {\partial \ln Z_{i}(N)}{\partial N}}.}$

Если число частиц достаточно велико, так что изменение химического потенциала при добавлении частицы в систему очень мало, то ^[28] Применяем экспоненциальную функцию к обеим сторонам, заменяя и переставляя,${\displaystyle N}$${\displaystyle \mu }$${\displaystyle \alpha _{i}\simeq -\mu /k_{\text{B}}T.}$${\displaystyle \alpha _{i}}$

${\displaystyle Z_{i}(N)/Z_{i}(N-1)=e^{-\mu /k_{\text{B}}T}.}$

Подставляя вышеприведенное в уравнение для и используя предыдущее определение для замены , получаем распределение Ферми–Дирака:${\displaystyle {\bar {n}}_{i}}$${\displaystyle \beta }$${\displaystyle 1/k_{\text{B}}T}$${\displaystyle \beta }$

${\displaystyle {\bar {n}}_{i}={\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}+1}}.}$

Подобно распределению Максвелла–Больцмана и распределению Бозе–Эйнштейна , распределение Ферми–Дирака также может быть получено методом средних значений Дарвина–Фаулера . ^[29]

Результат может быть достигнут путем прямого анализа множественностей системы и использования множителей Лагранжа . ^[30]

Предположим, что у нас есть несколько уровней энергии, помеченных индексом i , каждый уровень имеет энергию ε _i и содержит в общей сложности n _i частиц. Предположим, что каждый уровень содержит g _i различных подуровней, все из которых имеют одинаковую энергию и которые различимы. Например, две частицы могут иметь разные импульсы (т. е. их импульсы могут быть вдоль разных направлений), в этом случае они различимы друг от друга, но при этом они могут иметь одинаковую энергию. Значение g _i , связанное с уровнем i , называется «вырождением» этого уровня энергии. Принцип исключения Паули гласит, что только один фермион может занимать любой такой подуровень.

Число способов распределения n _i неразличимых частиц по g _i подуровням энергетического уровня, с максимумом в одну частицу на подуровень, определяется биномиальным коэффициентом , используя его комбинаторную интерпретацию :

${\displaystyle w(n_{i},g_{i})={\frac {g_{i}!}{n_{i}!(g_{i}-n_{i})!}}.}$

Например, распределение двух частиц по трем подуровням даст численность популяции 110, 101 или 011 для всех трех способов, что равно 3!/(2!1!).

Число способов, которыми может быть реализован набор чисел заполнения n _{i ,} является произведением способов, которыми может быть заселен каждый отдельный энергетический уровень:

${\displaystyle W=\prod _{i}w(n_{i},g_{i})=\prod _{i}{\frac {g_{i}!}{n_{i}!(g_{i}-n_{i})!}}.}$

Следуя той же процедуре, которая использовалась при выводе статистики Максвелла–Больцмана , мы хотим найти набор n _{i ,} для которого W максимизируется, при условии, что есть фиксированное число частиц и фиксированная энергия. Мы ограничиваем наше решение, используя множители Лагранжа, образующие функцию:

${\displaystyle f(n_{i})=\ln W+\alpha \left(N-\sum n_{i}\right)+\beta \left(E-\sum n_{i}\varepsilon _{i}\right).}$

Используя приближение Стирлинга для факториалов, взяв производную по n _i , приравняв результат к нулю и решив относительно n _{i ,} получаем числа популяции Ферми–Дирака:

${\displaystyle n_{i}={\frac {g_{i}}{e^{\alpha +\beta \varepsilon _{i}}+1}}.}$

Используя процесс, аналогичный описанному в статье о статистике Максвелла–Больцмана , можно термодинамически показать, что и , так что в конечном итоге вероятность того, что состояние будет занято, равна${\displaystyle \beta ={\tfrac {1}{k_{\text{B}}T}}}$${\displaystyle \alpha =-{\tfrac {\mu }{k_{\text{B}}T}}}$

${\displaystyle {\bar {n}}_{i}={\frac {n_{i}}{g_{i}}}={\frac {1}{e^{(\varepsilon _{i}-\mu )/k_{\text{B}}T}+1}}.}$

На Викискладе есть медиафайлы по теме «Распределение Ферми-Дирака» .

• Рейф, Ф. (1965). Основы статистической и тепловой физики . McGraw–Hill. ISBN 978-0-07-051800-1.
• Блейкмор, Дж. С. (2002). Статистика полупроводников. Довер. ISBN 978-0-486-49502-6.
• Киттель, Чарльз (1971). Введение в физику твердого тела (4-е изд.). Нью-Йорк: John Wiley & Sons. ISBN 978-0-471-14286-7. OCLC  300039591.