Спираль Ферма

Спираль, охватывающая одинаковую площадь за один оборот

{\displaystyle r=+a{\sqrt {\varphi }}} — Спираль Ферма: a>0, одна ветвь $r=+a{\sqrt {\varphi }}$

Спираль Ферма или параболическая спираль — это плоская кривая , обладающая свойством, что площадь между любыми двумя последовательными полными витками вокруг спирали инвариантна. В результате расстояние между витками растёт обратно пропорционально их расстоянию от центра спирали, в отличие от архимедовой спирали (для которой это расстояние инвариантно) и логарифмической спирали (для которой расстояние между витками пропорционально расстоянию от центра). Спирали Ферма названы в честь Пьера де Ферма . ^[1]

Их применение включает в себя непрерывное смешивание кривых, ^[1] моделирование роста растений и форм некоторых спиральных галактик , а также проектирование переменных конденсаторов , массивов отражателей солнечной энергии и циклотронов .

Координатное представление

Полярный

Представление спирали Ферма в полярных координатах $(r, φ)$ задается уравнением для $φ$ $\geq 0$ . $r=\pm a{\sqrt {\varphi }}$

Параметр представляет собой масштабный коэффициент, влияющий на размер спирали, но не на ее форму. $а$

Два выбора знака дают две ветви спирали, которые плавно сходятся в начале координат. Если бы те же самые переменные были переинтерпретированы как декартовы координаты , это было бы уравнение параболы с горизонтальной осью, которая снова имеет две ветви выше и ниже оси, сходящиеся в начале координат.

Декартов

Спираль Ферма с полярным уравнением может быть преобразована в декартовы координаты $($ $x$ $,$ $y$ $)$ с помощью стандартных формул преобразования $x$ $=$ $r$ $cos$ $φ$ и $y$ $=$ $r$ $sin$ $φ$ . Использование полярного уравнения для спирали для исключения $r$ из этих преобразований дает параметрические уравнения для одной ветви кривой: $r=\pm a{\sqrt {\varphi }}$

{\begin{cases}x(\varphi)=+a{\sqrt {\varphi }}\cos(\varphi )\\y(\varphi )=+a{\sqrt {\varphi }}\ грех(\varphi)\end{cases}}

и второй

{\begin{cases}x(\varphi )=-a{\sqrt {\varphi }}\cos(\varphi )\\y(\varphi )=-a{\sqrt {\varphi }}\sin(\varphi )\end{cases}}

Они генерируют точки ветвей кривой, когда параметр $φ$ изменяется в диапазоне положительных действительных чисел.

Для любого $(x, y),$ полученного таким образом, деление $x$ на $y$ отменяет части $a \sqrt φ$ параметрических уравнений, оставляя более простое уравнение $⁠ х / у ⁠ = cot φ$ . Из этого уравнения, заменив $φ$ на $φ = ⁠ г 2 / а 2 ⁠$ (переставленная форма полярного уравнения для спирали) и затем замена $r$ на $r = \sqrt x 2 + y 2$ (преобразование из декартовой системы в полярную) оставляет уравнение для спирали Ферма только с точки зрения $x$ и $y$ : Поскольку знак $a$ теряется при возведении в квадрат, это уравнение охватывает обе ветви кривой. ${\frac {x}{y}}=\cot \left({\frac {x^{2}+y^{2}}{a^{2}}}\right).$

Геометрические свойства

Спираль Ферма делит плоскость на две связанные и конгруэнтные области (схема: черная и белая)

Разделение самолета

Полная спираль Ферма (обе ветви) — это гладкая кривая без двойной точки , в отличие от архимедовой и гиперболической спирали . Подобно линии, окружности или параболе, она делит плоскость на две связанные области.

Определение сектора (светло-голубого) и угла наклона полюса $α$

Полярный склон

Из векторного исчисления в полярных координатах получается формула

\tan \alpha ={\frac {r'}{r}}

для полярного наклона и его угла $α$ между касательной кривой и соответствующей полярной окружностью (см. диаграмму).

Для спирали Ферма $r = a \sqrt φ$ получаем

\tan \alpha ={\frac {1}{2\varphi }}.

Следовательно, угол наклона монотонно уменьшается.

Кривизна

Из формулы

\kappa ={\frac {r^{2}+2(r')^{2}-r\,r''}{\left(r^{2}+(r')^{2}\right)^{\frac {3}{2}}}}

для кривизны кривой с полярным уравнением $r = r (φ)$ и его производными

{\begin{aligned}r'&={\frac {a}{2{\sqrt {\varphi }}}}={\frac {a^{2}}{2r}}\\r''&=-{\frac {a}{4{\sqrt {\varphi }}^{3}}}=-{\frac {a^{4}}{4r^{3}}}\end{aligned}}

получаем кривизну спирали Ферма: $\kappa (r)={\frac {2r\left(4r^{4}+3a^{4}\right)}{\left(4r^{4}+a^{4}\right)^{\frac {3}{2}}}}.$

В начале координат кривизна равна 0. Следовательно, полная кривая имеет в начале координат точку перегиба , а ось $x$ является ее касательной в этой точке.

Площадь между дугами

Площадь сектора спирали Ферма между двумя точками $(r (φ 1), φ 1)$ и $(r (φ 2), φ 2)$ равна

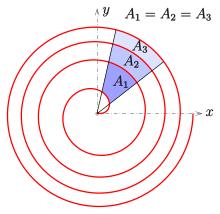
{\begin{aligned}{\underline {A}}&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\,d\varphi \\&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}a^{2}\varphi \,d\varphi \\&={\frac {a^{2}}{4}}\left(\varphi _{2}^{2}-\varphi _{1}^{2}\right)\\&={\frac {a^{2}}{4}}\left(\varphi _{2}+\varphi _{1}\right)\left(\varphi _{2}-\varphi _{1}\right).\end{aligned}}

Спираль Ферма: площадь между соседними дугами

$После$ увеличения обоих углов на $2π$ получаем

{\overline {A}}={\frac {a^{2}}{4}}\left(\varphi _{2}+\varphi _{1}+4\pi \right)\left(\varphi _{2}-\varphi _{1}\right)={\underline {A}}+a^{2}\pi \left(\varphi _{2}-\varphi _{1}\right).

Следовательно, площадь $A$ области между двумя соседними дугами зависит $только$ от разности двух углов, а не от самих углов. $A=a^{2}\pi \left(\varphi _{2}-\varphi _{1}\right).$

Для примера, показанного на схеме, все соседние полосы имеют одинаковую площадь: $A 1 = A 2 = A 3$ .

Это свойство используется в электротехнике для создания переменных конденсаторов . ^[2]

Частный случай, связанный с Ферма

В 1636 году Ферма написал письмо ^[3] Марину Мерсенну , в котором содержался следующий частный случай:

Пусть $φ 1 = 0, φ 2 = 2 π$ ; тогда площадь черной области (см. диаграмму) равна $A 0 = a 2 π 2$ , что составляет половину площади круга $K 0$ с радиусом $r (2 π)$ . Области между соседними кривыми (белая, синяя, желтая) имеют одинаковую площадь $A = 2 a 2 π 2$ . Следовательно:

Площадь между двумя дугами спирали после полного оборота равна площади круга $K 0$ .

Длина дуги

Длину дуги спирали Ферма между двумя точками $($ $r (φi), φi) можно$ вычислить с помощью интеграла :

${\begin{aligned}L&=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}}\,d\varphi \\&={\frac {a}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {{\frac {1}{\varphi }}+4\varphi }}\,d\varphi .\end{aligned}}$

Этот интеграл приводит к эллиптическому интегралу , который можно решить численно.

Длина дуги положительной ветви спирали Ферма от начала координат может быть также определена гипергеометрическими функциями $2 F 1 (a, b; c; z)$ и неполной бета-функцией $B(z; a, b)$ : ^[4]

${\begin{aligned}L&=a\cdot {\sqrt {\varphi }}\cdot \operatorname {_{2}F_{1}} \left(-{\tfrac {1}{2}},\,{\tfrac {1}{4}};\,{\tfrac {5}{4}};\,-4\cdot \varphi ^{2}\right)\\&=a\cdot {\frac {1-i}{8}}\cdot \operatorname {B} \left(-4\cdot \varphi ^{2};\,{\tfrac {1}{4}},\,{\tfrac {3}{2}}\right)\\\end{aligned}}$

Инверсия спирали Ферма (зеленая) представляет собой литуус (синий).

Инверсия круга

Инверсия на единичной окружности имеет в полярных координатах простое описание $(r, φ) \mapsto (⁠ 1 / г ⁠, φ)$ .

Образ спирали Ферма $r = a \sqrt φ$ при инверсии на единичной окружности представляет собой спираль литууса с полярным уравнением. Когда $φ$ $=$ $⁠$ $r={\frac {1}{a{\sqrt {\varphi }}}}.$ $1 / а 2 ⁠$ , обе кривые пересекаются в фиксированной точке на единичной окружности.
Касательная ( ось $x$ ) в точке перегиба (начале координат) спирали Ферма отображается сама на себя и является асимптотической линией спирали литууса.

Золотое сечение и золотой угол

В дисковом филлотаксисе , как в подсолнечнике и маргаритке, сетка спиралей происходит в числах Фибоначчи, потому что расхождение (угол последовательности в одиночной спиральной компоновке) приближается к золотому сечению . Форма спиралей зависит от роста элементов, генерируемых последовательно. В зрелом дисковом филлотаксисе , когда все элементы имеют одинаковый размер, форма спиралей в идеале соответствует форме спиралей Ферма. Это происходит потому, что спираль Ферма пересекает равные кольца за равные обороты. Полная модель, предложенная Х. Фогелем в 1979 году ^[5] , выглядит следующим образом:

${\begin{aligned}r&=c{\sqrt {n}},\\\theta &=n\times 137.508^{\circ },\end{aligned}}$

где $θ$ — угол, $r$ — радиус или расстояние от центра, $n$ — индекс цветка, а $c$ — постоянный масштабный коэффициент. Угол 137,508° — это золотой угол , который аппроксимируется отношениями чисел Фибоначчи . ^[6]

Рисунок цветочков, созданный моделью Фогеля (центральное изображение). На двух других изображениях показаны рисунки для немного отличающихся значений угла.

Полученный спиральный узор из единичных дисков следует отличать от спиралей Дойла — узоров, образованных касательными дисками геометрически увеличивающихся радиусов, размещенными на логарифмических спиралях .

Солнечные электростанции

Спираль Ферма также оказалась эффективной схемой для зеркал концентрированных солнечных электростанций . ^[7]

Смотрите также

Ссылки

^ ab Lekkas, Anastasios M.; Dahl, Andreas R.; Breivik, Morten; Fossen, Thor I. (2013). "Continuous-Curvature Path Generation Using Fermat's Spiral" (PDF) . Моделирование, идентификация и управление . 34 (4): 183–198. ISSN 1890-1328. Архивировано из оригинала (PDF) 28.10.2020.
^ Вике, Фриц (2013). Einführung in die höhere Mathematik . Спрингер-Верлаг. п. 414. ИСБН 978-3-662-36804-6.
^ Таннери, Пол (ред.). «Письмо Ферма в Мерсенне от 3 июня 1636 года». Творения Ферма . Том. 3. п. 277.
^ Weisstein, Eric W. "Спираль Ферма". MathWorld . Получено 2023-02-04 .
^ Фогель, Х. (1979). «Лучший способ построить головку подсолнечника». Математические биологические науки . 44 ( 3–4 ): 179–189 . doi :10.1016/0025-5564(79)90080-4.
^ Прусинкевич, Пшемыслав ; Линденмайер, Аристид (1990). Алгоритмическая красота растений. Springer-Verlag. С. 101–107. ISBN 978-0-387-97297-8.
^ Нун, Кори Дж.; Торрилхон, Мануэль; Мицос, Александр (декабрь 2011 г.). «Оптимизация поля гелиостата: новая вычислительно эффективная модель и биомиметическая компоновка». Солнечная энергия . 86 (2): 792– 803. doi :10.1016/j.solener.2011.12.007.

Дальнейшее чтение

Лоуренс, Дж. Деннис (1972). Каталог специальных плоских кривых . Dover Publications. стр. 31, 186. ISBN 0-486-60288-5.

Внешние ссылки

«Спираль Ферма». Энциклопедия математики . EMS Press . 2001 [1994].
Онлайн-исследование с использованием JSXGraph (JavaScript)
Естественные спирали Ферма, на сайте sciencenews.org

[Lekkas-1] Lekkas, Anastasios M.; Dahl, Andreas R.; Breivik, Morten; Fossen, Thor I. (2013). "Continuous-Curvature Path Generation Using Fermat's Spiral" (PDF) . Моделирование, идентификация и управление . 34 (4): 183–198. ISSN 1890-1328. Архивировано из оригинала (PDF) 28.10.2020.

[2] Вике, Фриц (2013). Einführung in die höhere Mathematik . Спрингер-Верлаг. п. 414. ИСБН 978-3-662-36804-6.

[Fermat-3] Таннери, Пол (ред.). «Письмо Ферма в Мерсенне от 3 июня 1636 года». Творения Ферма . Том. 3. п. 277.

[4] Weisstein, Eric W. "Спираль Ферма". MathWorld . Получено 2023-02-04 .

[5] Фогель, Х. (1979). «Лучший способ построить головку подсолнечника». Математические биологические науки . 44 ( 3–4 ): 179–189 . doi :10.1016/0025-5564(79)90080-4.

[6] Прусинкевич, Пшемыслав ; Линденмайер, Аристид (1990). Алгоритмическая красота растений. Springer-Verlag. С. 101–107. ISBN 978-0-387-97297-8.

[7] Нун, Кори Дж.; Торрилхон, Мануэль; Мицос, Александр (декабрь 2011 г.). «Оптимизация поля гелиостата: новая вычислительно эффективная модель и биомиметическая компоновка». Солнечная энергия . 86 (2): 792– 803. doi :10.1016/j.solener.2011.12.007.