Внешняя баллистика
Внешняя баллистика или внешняя баллистика — это часть баллистики , которая занимается поведением снаряда в полете. Снаряд может быть с двигателем или без, управляемым или неуправляемым, стабилизированным вращением или плавником, летящим в атмосфере или в вакууме космоса, но, безусловно, летящим под воздействием гравитационного поля. [1]
Снаряды, запускаемые из пушки, могут быть неактивными, получая всю свою скорость от воспламенения метательного заряда до тех пор, пока снаряд не покинет ствол пушки . [2] Однако анализ внешней баллистики также имеет дело с траекториями снарядов, запускаемых с помощью ракеты, и ракет, запускаемых из пушки; и ракет, которые приобретают всю свою скорость на траектории от внутренней баллистики их бортовой двигательной системы, будь то ракетный двигатель или воздушно-реактивный двигатель, как во время фазы разгона, так и после выгорания двигателя. Внешняя баллистика также касается свободного полета других снарядов, таких как мячи , стрелы и т. д.
Силы, действующие на снаряд
В полете основными или основными силами, действующими на снаряд, являются сила тяжести , сопротивление и, если присутствует, ветер ; в полете с работающим двигателем — тяга; а в управляемом полете — силы, сообщаемые управляющими поверхностями.
В приложениях внешней баллистики стрелкового оружия гравитация придает снаряду ускорение вниз, заставляя его падать с линии прицеливания . Сопротивление или сопротивление воздуха замедляет снаряд с силой, пропорциональной квадрату скорости. Ветер заставляет снаряд отклоняться от своей траектории. Во время полета гравитация, сопротивление и ветер оказывают большое влияние на траекторию снаряда и должны учитываться при прогнозировании того, как будет двигаться снаряд.
Для средних и больших расстояний и времени полета, помимо силы тяжести, сопротивления воздуха и ветра, необходимо учитывать несколько промежуточных или мезопеременных, описанных в параграфе внешних факторов для стрелкового оружия. Мезопеременные могут стать значимыми для пользователей огнестрельного оружия, которым приходится иметь дело со сценариями стрельбы под углом или на больших расстояниях, но редко имеют значение на обычных дистанциях охоты и стрельбы по мишеням.
Для дальних и очень дальних дистанций стрельбы из стрелкового оружия и времени полета второстепенные эффекты и силы, такие как описанные в параграфе о факторах большой дальности, становятся важными и должны быть приняты во внимание. Практические эффекты этих второстепенных переменных, как правило, не имеют значения для большинства пользователей огнестрельного оружия, поскольку нормальный разброс групп на коротких и средних дистанциях преобладает над влиянием, которое эти эффекты оказывают на траектории снарядов .
На очень больших расстояниях артиллерия должна стрелять снарядами по траекториям, которые даже приблизительно не являются прямыми; они ближе к параболическим , хотя сопротивление воздуха влияет на это. Снаряды очень большой дальности подвержены значительным отклонениям, в зависимости от обстоятельств, от линии к цели; и все внешние факторы и факторы большой дальности должны быть приняты во внимание при прицеливании. В случаях артиллерии очень большого калибра , как, например, Paris Gun , очень тонкие эффекты, которые не рассматриваются в этой статье, могут дополнительно уточнить решения по прицеливанию.
В случае баллистических ракет высота полета также имеет существенное значение, поскольку часть полета происходит в почти вакуумной среде над вращающейся Землей, постоянно перемещая цель относительно того места, где она находилась во время запуска.
Стабилизация несферических снарядов во время полета
Для стабилизации несферических снарядов во время полета можно использовать два метода:
- Снаряды, такие как стрелы или стреловидные подкалиберные снаряды , такие как бронебойный, оперенный, отделяющийся подкалиберный снаряд M829 (APFSDS), достигают устойчивости, перемещая свой центр давления (ЦД) за центр масс (ЦМ) с помощью хвостовых поверхностей. Условие ЦД за ЦМ обеспечивает стабильный полет снаряда, то есть снаряд не перевернется во время полета через атмосферу из-за аэродинамических сил.
- Снаряды, такие как пули стрелкового оружия и артиллерийские снаряды, должны иметь дело с тем, что их CP находится перед их CM, что дестабилизирует эти снаряды во время полета. Для стабилизации таких снарядов снаряд вращается вокруг своей продольной (ведущей к отстающей) оси. Вращающаяся масса создает гироскопические силы, которые удерживают ось длины пули устойчивой к дестабилизирующему опрокидывающему моменту CP, находящегося перед CM.
Основные эффекты внешней баллистики
Падение и траектория полета снаряда/пули

Влияние гравитации на снаряд в полете часто называют падением снаряда или падением пули. Важно понимать влияние гравитации при обнулении прицельных компонентов оружия. Чтобы правильно спланировать падение снаряда и компенсировать его, необходимо понимать параболические траектории .
Падение снаряда/пули
Для того чтобы снаряд поразил какую-либо удаленную цель, ствол должен быть наклонен под положительным углом возвышения относительно цели. Это связано с тем, что снаряд начнет реагировать на воздействие гравитации в тот момент, когда он освободится от механических ограничений канала ствола. Воображаемая линия, проходящая вниз по центральной оси канала ствола и уходящая в бесконечность, называется линией вылета и является линией, по которой снаряд покидает ствол. Из-за воздействия гравитации снаряд никогда не может поразить цель, расположенную выше линии вылета. Когда положительно наклоненный снаряд движется вниз по дальности, он описывает дугу ниже линии вылета, поскольку отклоняется от своего первоначального пути под действием силы тяжести. Падение снаряда/пули определяется как вертикальное расстояние снаряда ниже линии вылета из канала ствола. Даже когда линия вылета наклонена вверх или вниз, падение снаряда все равно определяется как расстояние между пулей и линией вылета в любой точке вдоль траектории. Падение снаряда не описывает фактическую траекторию снаряда. Однако знание падения снаряда полезно при проведении прямого сравнения двух различных снарядов относительно формы их траекторий, сравнивая влияние таких переменных, как скорость и сопротивление.
Траектория полета снаряда/пули
Для поражения удаленной цели требуется соответствующий положительный угол возвышения, который достигается путем наклона линии прицеливания от глаза стрелка через осевую линию прицельной системы вниз к линии вылета. Этого можно добиться простой механической регулировкой прицела вниз или путем закрепления всей прицельной системы на наклонном креплении с известным наклоном вниз, или комбинацией того и другого. Эта процедура имеет эффект подъема дула, когда ствол должен быть впоследствии поднят для выравнивания прицела с целью. Снаряд, покидающий дуло под заданным углом возвышения, следует по баллистической траектории , характеристики которой зависят от различных факторов, таких как начальная скорость, сила тяжести и аэродинамическое сопротивление. Эта баллистическая траектория называется траекторией пули. Если снаряд стабилизирован вращением, аэродинамические силы также предсказуемо слегка отклонят траекторию вправо, если нарезка использует «правую закрутку». Некоторые стволы нарезаны с левым поворотом, и в результате пуля будет лететь по дуге влево. Поэтому, чтобы компенсировать это отклонение траектории, прицелы также должны быть скорректированы влево или вправо соответственно. Постоянный ветер также предсказуемо влияет на траекторию пули, слегка смещая ее влево или вправо и немного вверх и вниз, в зависимости от направления ветра. Величина этих отклонений также зависит от того, находится ли пуля на восходящем или нисходящем склоне траектории, из-за явления, называемого «рысканием покоя», когда вращающаяся пуля имеет тенденцию устойчиво и предсказуемо выравниваться немного не по центру от траектории своей точечной массы. Тем не менее, каждое из этих возмущений траектории можно предсказать, как только будут установлены аэродинамические коэффициенты снаряда, посредством комбинации подробного аналитического моделирования и измерений на испытательном полигоне.
Анализ траектории снаряда/пули очень полезен для стрелков, поскольку он позволяет им составлять баллистические таблицы , которые предсказывают, сколько поправок на вертикальную высоту и горизонтальное отклонение необходимо применить к линии прицеливания для выстрелов на различных известных расстояниях. Самые подробные баллистические таблицы разработаны для дальнобойной артиллерии и основаны на анализе траектории с шестью степенями свободы, который учитывает аэродинамическое поведение вдоль трех осевых направлений — возвышение, дальность и отклонение — и трех направлений вращения — тангаж, рыскание и вращение. Для приложений со стрелковым оружием моделирование траектории часто можно упростить до расчетов, включающих только четыре из этих степеней свободы, объединяя эффекты тангажа, рыскания и вращения в эффект рыскания покоя для учета отклонения траектории. После составления подробных таблиц дальности стрелки могут относительно быстро настраивать прицелы на основе дальности до цели, ветра, температуры и влажности воздуха и других геометрических соображений, таких как разница высот местности.
Значения траектории снаряда определяются как высотой прицела, или расстоянием линии прицеливания над осевой линией канала ствола, так и расстоянием, на котором прицелы обнуляются, что, в свою очередь, определяет угол возвышения. Снаряд, летящий по баллистической траектории, имеет как прямое, так и вертикальное движение. Прямое движение замедляется из-за сопротивления воздуха, а в моделировании точечной массы вертикальное движение зависит от комбинации угла возвышения и силы тяжести. Первоначально снаряд поднимается относительно линии прицеливания или горизонтальной плоскости прицеливания. В конечном итоге снаряд достигает своей вершины (высшей точки параболы траектории), где вертикальная составляющая скорости спадает до нуля под действием силы тяжести, а затем начинает снижаться, в конечном итоге ударяясь о землю. Чем больше расстояние до предполагаемой цели, тем больше угол возвышения и выше вершина.
Траектория снаряда пересекает горизонтальную плоскость прицеливания два раза. Точка, ближайшая к оружию, возникает, когда пуля поднимается по линии прицеливания, и называется ближним нулем. Вторая точка возникает, когда снаряд опускается по линии прицеливания. Она называется дальним нулем и определяет текущее расстояние прицеливания для оружия. Траектория снаряда численно описывается как расстояния выше или ниже горизонтальной плоскости прицеливания в различных точках вдоль траектории. Это отличается от падения снаряда, которое относится к плоскости, содержащей линию вылета, независимо от угла возвышения. Поскольку каждый из этих двух параметров использует разные опорные данные, может возникнуть значительная путаница, поскольку даже если снаряд отслеживается значительно ниже линии вылета, он все равно может набирать фактическую и значительную высоту по отношению к линии прицеливания, а также к поверхности Земли в случае горизонтального или почти горизонтального выстрела, сделанного над ровной местностью.
Максимальная дальность прямого выстрела и нулевой бой
Знание траектории падения и траектории снаряда имеет некоторые практические преимущества для стрелков, даже если оно не описывает фактическую траекторию снаряда. Например, если вертикальное положение снаряда на определенном расстоянии досягаемости находится в пределах вертикальной высоты целевой области, которую стрелок хочет поразить, точка прицеливания не обязательно должна быть скорректирована на этом расстоянии; снаряд считается имеющим достаточно плоскую траекторию прямого выстрела для этой конкретной цели. [3] Также известная как «боевой ноль», максимальная дальность прямого выстрела также важна для военных. Солдатам предписывается стрелять по любой цели в пределах этого диапазона, просто помещая прицел своего оружия на центр масс вражеской цели. Любые ошибки в оценке дальности тактически не имеют значения, поскольку хорошо прицельный выстрел поразит торс вражеского солдата. Текущая тенденция к приподнятым прицелам и высокоскоростным патронам в штурмовых винтовках отчасти обусловлена желанием увеличить максимальную дальность прямого выстрела, что делает винтовку более простой в использовании. [4] [5] [6]
Сопротивление движению

Математические модели , такие как вычислительная гидродинамика, используются для расчета эффектов сопротивления воздуха; они довольно сложны и пока не вполне надежны, но исследования продолжаются. [7] Поэтому наиболее надежным методом установления необходимых аэродинамических свойств снаряда для надлежащего описания траекторий полета является эмпирическое измерение.
Исправлены модели кривых сопротивления, созданные для снарядов стандартной формы.

Использование баллистических таблиц или программного обеспечения для баллистики, основанного на методе Маевского/Сиаччи и модели сопротивления G1 , представленной в 1881 году, является наиболее распространенным методом, используемым для работы с внешней баллистикой. Снаряды описываются баллистическим коэффициентом , или BC, который объединяет сопротивление воздуха формы пули ( коэффициент сопротивления ) и ее плотность сечения (функция массы и диаметра пули).
Замедление из-за сопротивления , которое испытает снаряд с массой m , скоростью v и диаметром d, пропорционально 1/BC, 1/ m , v² и d² . BC дает отношение баллистической эффективности по сравнению со стандартным снарядом G1, который является фиктивным снарядом с плоским основанием, длиной 3,28 калибра/диаметра и касательной радиусом 2 калибра/диаметра для точки. Стандартный снаряд G1 происходит от стандартного эталонного снаряда "C", определенного немецким производителем стали, боеприпасов и вооружения Krupp в 1881 году. Стандартный снаряд модели G1 имеет BC, равный 1. [8] Французская Гаврская комиссия решила использовать этот снаряд в качестве своего первого эталонного снаряда, дав ему название G1. [9] [10]
Спортивные пули калибра d от 0,177 до 0,50 дюймов (от 4,50 до 12,7 мм ) имеют G1 BC в диапазоне от 0,12 до чуть более 1,00, где 1,00 является наиболее аэродинамичным, а 0,12 — наименее. Пули с очень низким сопротивлением с BC ≥ 1,10 могут быть спроектированы и изготовлены на прецизионных токарных станках с ЧПУ из монометаллических стержней, но их часто приходится стрелять из изготовленных на заказ полнокалиберных винтовок со специальными стволами. [11]
Плотность сечения является очень важным аспектом снаряда или пули, и для круглого снаряда, такого как пуля, это отношение площади лобной поверхности (половина диаметра пули в квадрате, умноженная на пи ) к массе пули. Поскольку для заданной формы пули лобная поверхность увеличивается как квадрат калибра, а масса увеличивается как куб диаметра, то плотность сечения растет линейно с диаметром канала ствола. Поскольку BC объединяет форму и плотность сечения, модель снаряда G1 в половинном масштабе будет иметь BC 0,5, а модель в четверть масштаба будет иметь BC 0,25.
Поскольку снаряды разной формы будут по-разному реагировать на изменения скорости (особенно между сверхзвуковыми и дозвуковыми скоростями), BC, предоставляемый производителем пули, будет средним BC, который представляет общий диапазон скоростей для этой пули. Для винтовочных пуль это, вероятно, будет сверхзвуковая скорость, для пистолетных пуль это, вероятно, будет дозвуковая. Для снарядов, которые проходят через сверхзвуковые , трансзвуковые и дозвуковые режимы полета, BC не очень хорошо аппроксимируется одной константой, но считается функцией BC (M) числа Маха M; здесь M равно скорости снаряда, деленной на скорость звука . Во время полета снаряда M будет уменьшаться, и поэтому (в большинстве случаев) BC также будет уменьшаться.
Большинство баллистических таблиц или программного обеспечения принимают как должное, что одна конкретная функция сопротивления правильно описывает сопротивление и, следовательно, летные характеристики пули, связанные с ее баллистическим коэффициентом. Эти модели не различают типы или формы пуль wadcutter , flat-base, spitzer, boat-tail, very-low-drag и т. д. Они предполагают одну неизменную функцию сопротивления, как указано в опубликованном BC.
Однако доступны несколько моделей кривых сопротивления, оптимизированных для нескольких стандартных форм снарядов. Полученные фиксированные модели кривых сопротивления для нескольких стандартных форм или типов снарядов называются:

- G1 или Ingalls (плоское основание с тупым носом 2 калибра — безусловно, самый популярный)
- G2 (снаряд Aberdeen J)
- G5 (короткая 7,5° боатт-тейл, 6,19 калибра, длинная касательная оживалка )
- G6 (плоское основание, длинная секущая стрела 6 калибров )
- G7 (длинная 7,5° хвостовая часть, тангенциальная оживальная часть длиной 10 калибров, предпочитаемая некоторыми производителями для пуль с очень низким сопротивлением [12] )
- G8 (плоское основание, 10 калибров, длинный секущий оживальный ствол)
- GL (тупой свинцовый носик)
Как различные скоростные режимы влияют на винтовочные пули калибра .338, можно увидеть в брошюре продукта .338 Lapua Magnum, в которой указаны данные G1 BC, установленные доплеровским радаром. [13] [14] Причина публикации данных, подобных этой брошюре, заключается в том, что модель Siacci/Mayevski G1 не может быть настроена на поведение сопротивления конкретного снаряда, форма которого значительно отличается от формы используемого эталонного снаряда. Некоторые разработчики баллистического программного обеспечения, которые основывали свои программы на модели Siacci/Mayevski G1, предоставляют пользователю возможность вводить несколько различных констант G1 BC для различных скоростных режимов для расчета баллистических прогнозов, которые лучше соответствуют поведению полета пули на больших расстояниях по сравнению с расчетами, которые используют только одну константу BC.
Приведенный выше пример иллюстрирует центральную проблему моделей с фиксированной кривой сопротивления. Эти модели будут давать удовлетворительные точные прогнозы только в том случае, если интересующий снаряд имеет ту же форму, что и эталонный снаряд, или форму, которая очень похожа на эталонный снаряд. Любое отклонение от формы эталонного снаряда приведет к менее точным прогнозам. [15] [16] Насколько снаряд отклоняется от примененного эталонного снаряда, математически выражается форм-фактором ( i ). [17] Форм-фактор можно использовать для сравнения сопротивления, испытываемого интересующим снарядом, с сопротивлением, испытываемым используемым эталонным снарядом на заданной скорости (диапазоне). Проблема того, что фактическая кривая сопротивления снаряда может значительно отклоняться от фиксированной кривой сопротивления любого используемого эталонного снаряда, систематически ограничивает традиционный подход к моделированию сопротивления сопротивлению. Однако относительная простота делает его понятным и понятным для широкой публики стрелков, и, следовательно, он также популярен среди разработчиков баллистического программного обеспечения для прогнозирования и производителей пуль, которые хотят продавать свою продукцию.
Более продвинутые модели сопротивления
Модель Пейса
Еще одной попыткой создания баллистического калькулятора является модель, представленная в 1980 году доктором Артуром Дж. Пейсой. [18] Доктор Пейсой утверждает на своем веб-сайте, что его метод последовательно способен предсказывать траектории (сверхзвуковых) винтовочных пуль в пределах 2,5 мм (0,1 дюйма) и скорости пуль в пределах 0,3 м/с (1 фут/с) до 914 м (1000 ярдов) в теории. [19] Модель Пейсой представляет собой решение в замкнутой форме .
Модель Pejsa может предсказать снаряд в заданном режиме полета (например, сверхзвуковой режим полета) всего с двумя измерениями скорости, расстоянием между указанными измерениями скорости и наклоном или постоянным фактором замедления. [20] Модель позволяет кривой сопротивления изменять наклоны (истинный/калиброванный) или кривизну в трех различных точках. [21] Данные измерения скорости на ближнем расстоянии могут быть предоставлены вокруг ключевых точек перегиба, что позволяет более точно рассчитать скорость замедления снаряда, очень похожую на таблицу Маха против CD. Модель Pejsa позволяет настраивать фактор наклона для учета тонких различий в скорости замедления различных форм и размеров пуль. Он варьируется от 0,1 (пули с плоским носом) до 0,9 ( пули с очень низким сопротивлением ). Если этот фактор наклона или постоянного фактора замедления неизвестен, используется значение по умолчанию 0,5. С помощью измерений тестовых стрельб можно определить постоянную наклона для конкретной комбинации пули/винтовочной системы/стрелка. Эти испытательные стрельбы предпочтительно проводить на 60%, а для баллистических прогнозов на экстремально дальние расстояния также на 80–90% сверхзвукового диапазона интересующих снарядов, избегая при этом нерегулярных трансзвуковых эффектов. При этом модель Пейсы можно легко настроить. Практическим недостатком модели Пейсы является то, что точные измерения скорости снаряда на ближней дистанции для обеспечения этих лучших прогнозов не могут быть легко выполнены подавляющим большинством любителей стрельбы.
Средний коэффициент замедления может быть вычислен для любого заданного постоянного коэффициента наклона, если известны точки данных о скорости и расстояние между указанными измерениями скорости. Очевидно, что это верно только в пределах одного и того же режима полета. Под скоростью подразумевается фактическая скорость , поскольку скорость является векторной величиной, а скорость является величиной вектора скорости. Поскольку степенная функция не имеет постоянной кривизны , нельзя использовать простое среднее значение хорды . Модель Пейсы использует взвешенный средний коэффициент замедления, взвешенный на расстоянии 0,25. Более близкая скорость имеет больший вес. Коэффициент замедления измеряется в футах, тогда как расстояние измеряется в ярдах, поэтому 0,25 × 3,0 = 0,75, в некоторых местах используется 0,8, а не 0,75. 0,8 получается округлением, чтобы обеспечить легкий ввод на ручных калькуляторах. Поскольку модель Pejsa не использует простое взвешенное среднее значение хорды, два измерения скорости используются для нахождения коэффициента замедления среднего значения хорды на середине диапазона между двумя точками измерения скорости, ограничивая его точностью на коротком расстоянии. Чтобы найти начальный коэффициент замедления, доктор Pejsa приводит два отдельных уравнения в своих двух книгах. Первое включает степенную функцию. [22] Второе уравнение идентично тому, которое используется для нахождения взвешенного среднего значения при R / 4; добавьте N × (R / 2), где R - диапазон в футах, к коэффициенту замедления среднего значения хорды на середине диапазона, а N - постоянный фактор наклона. [23] После того, как найден начальный коэффициент замедления, используется обратная процедура для нахождения взвешенного среднего значения при R / 4; начальный коэффициент замедления минус N × (R / 4). Другими словами, N используется в качестве наклона линии хорды. Доктор Пейса утверждает, что он разложил свою формулу капли в степенной ряд , чтобы доказать, что средневзвешенный коэффициент запаздывания при R / 4 является хорошим приближением. Для этого доктор Пейса сравнил разложение в степенной ряд своей формулы капли с разложением в степенной ряд какой-то другой неназванной формулы капли, чтобы прийти к своим выводам. Четвертый член в обоих степенных рядах совпал, когда коэффициент запаздывания в диапазоне 0,25 использовался в формуле капли Пейсы. Четвертый член также был первым членом, в котором использовалось N. Более высокие члены, включающие N, были незначительными и исчезали при N = 0,36, что, по словам доктора Пейсы, было счастливым совпадением, обеспечивающим чрезвычайно точное линейное приближение, особенно для N около 0,36. Если используется функция коэффициента запаздывания, то можно получить точные средние значения для любого N, поскольку из исчисления тривиально найти среднее значение любой интегрируемой функции . [24] Доктор Пейса утверждает, что коэффициент запаздывания можно смоделировать с помощью C × V Nгде C — подгоночный коэффициент, который исчезает при выводе формулы падения, а N — коэффициент постоянной наклона. [25]
Коэффициент замедления равен квадрату скорости, делённому на скорость замедления A. Использование среднего коэффициента замедления позволяет представить модель Пейсы в виде замкнутого выражения в заданном режиме полета.

Для того чтобы разрешить использование баллистического коэффициента G1 вместо данных о скорости, доктор Пейса предоставил две эталонные кривые сопротивления. Первая эталонная кривая сопротивления основана исключительно на функции скорости замедления Сиаччи/Маевского. Вторая эталонная кривая сопротивления скорректирована так, чтобы она была равна функции скорости замедления Сиаччи/Маевского при скорости снаряда 2600 футов в секунду (792,5 м/с) с использованием винтовочной пули Spitzer .30-06 Springfield Cartridge, Ball, Caliber .30 M2 152 грана (9,8 г) с коэффициентом наклона или постоянной замедления 0,5 в сверхзвуковом режиме полета. В других режимах полета вторая эталонная модель кривой сопротивления Пейсы использует коэффициенты постоянной наклона 0,0 или -4,0. Эти постоянные факторы замедления можно проверить, выполнив формулы Пейсы (сегменты кривой сопротивления соответствуют форме V (2 - N) / C, а сегменты кривой коэффициента замедления соответствуют форме V 2 / (V (2 - N) / C) = C × V N , где C - подгоночный коэффициент). Эмпирические тестовые данные, которые Пейса использовал для определения точной формы своей выбранной эталонной кривой сопротивления и предопределенной математической функции, которая возвращает коэффициент замедления при заданном числе Маха, были предоставлены военными США для пули Cartridge, Ball, Caliber .30 M2. Расчет функции коэффициента замедления также включает плотность воздуха, о которой Пейса явно не упомянул. Модель Siacci/Mayevski G1 использует следующую параметризацию замедления (60 °F, 30 дюймов рт. ст. и влажность 67%, плотность воздуха ρ = 1,2209 кг/м 3 ). [26] Доктор Пейса предлагает использовать вторую кривую сопротивления, поскольку кривая сопротивления Siacci/Mayevski G1 не обеспечивает хорошего соответствия для современных пуль Spitzer. [27] Чтобы получить соответствующие коэффициенты замедления для оптимального моделирования на больших расстояниях, доктор Пейса предложил использовать точные данные измерений скорости снаряда на ближней дистанции для конкретного снаряда, чтобы эмпирически вывести средний коэффициент замедления, а не использовать средний коэффициент замедления, полученный из эталонной кривой сопротивления. Кроме того, он предложил использовать боеприпасы с уменьшенными зарядами метательного заряда, чтобы эмпирически проверить фактическое поведение полета снаряда на более низких скоростях. При работе с уменьшенными зарядами метательного заряда необходимо проявлять максимальную осторожность, чтобы избежать опасных или катастрофических условий (детонаций), которые могут возникнуть при стрельбе экспериментальными зарядами в огнестрельном оружии. [21]
Модель Мангеса
Хотя и не так хорошо известна, как модель Пейсы, дополнительная альтернативная баллистическая модель была представлена в 1989 году полковником Даффом Мангесом (армия США в отставке) на 11-м Международном баллистическом симпозиуме по готовности к обороне (ADPA), состоявшемся в Брюссельском конгресс-центре, Брюссель, Бельгия, 9–11 мая 1989 года. Доклад под названием «Замкнутые траекторные решения для систем оружия прямого огня» появился в трудах, том 1, Динамика движения, Динамика запуска, Динамика полета, страницы 665–674. Первоначально задуманная для моделирования сопротивления снаряда для боеприпасов 120-мм танковой пушки , новая формула коэффициента сопротивления впоследствии была применена к баллистическим траекториям винтовочных боеприпасов центрального выстрела с результатами, сопоставимыми с заявленными для модели Пейсы.
Модель Мангеса использует теоретический подход первых принципов, который избегает кривых "G" и "баллистических коэффициентов", основанных на стандартной кривых G1 и других кривых подобия. Теоретическое описание состоит из трех основных частей. Первая заключается в разработке и решении формулировки двумерных дифференциальных уравнений движения, управляющих плоскими траекториями точечных массовых снарядов, путем математического определения набора квадратур, которые допускают замкнутые решения для дифференциальных уравнений движения траектории. Генерируется последовательность последовательных приближенных функций коэффициента сопротивления, которые быстро сходятся к фактическим наблюдаемым данным сопротивления. Модели вакуумной траектории, упрощенной аэродинамики, закона сопротивления Д'Антонио и Эйлера являются особыми случаями. Таким образом, закон сопротивления Мангеса обеспечивает объединяющее влияние по отношению к более ранним моделям, используемым для получения двумерных замкнутых решений уравнений движения точечной массы. Третья цель этой статьи заключается в описании процедуры подгонки наименьших квадратов для получения новых функций сопротивления из наблюдаемых экспериментальных данных. Автор утверждает, что результаты демонстрируют превосходное соответствие с числовыми расчетами с шестью степенями свободы для современных танковых боеприпасов и имеющимися опубликованными таблицами стрельбы для винтовочных боеприпасов центрального воспламенения, имеющих большое разнообразие форм и размеров.
Приложение Microsoft Excel было создано, которое использует наименьшие квадраты коэффициентов сопротивления, полученных в аэродинамической трубе. В качестве альтернативы, предоставленные производителем данные баллистической траектории или полученные данные скорости Доплера могут быть также подобраны для калибровки модели. Затем приложение Excel использует пользовательские макрокоманды для расчета интересующих переменных траектории. Используется модифицированный алгоритм интеграции Рунге-Кутты 4-го порядка . Как и Пейса, полковник Мангес заявляет о точности винтовки с центральным выстрелом до ближайшей десятой доли дюйма для положения пули и ближайшего фута в секунду для скорости снаряда.
Труды 11-го Международного баллистического симпозиума доступны на веб-сайте Национальной оборонно-промышленной ассоциации (NDIA) http://www.ndia.org/Resources/Pages/Publication_Catalog.aspx Архивировано 26 января 2012 г. на Wayback Machine .
Модель шести степеней свободы
Также доступны продвинутые профессиональные баллистические модели, такие как PRODAS. Они основаны на расчетах с шестью степенями свободы (6 DoF). Моделирование с 6 DoF учитывает положение x, y и z в пространстве вместе со скоростями тангажа, рыскания и крена снарядов. Моделирование с 6 DoF требует такого сложного ввода данных, знания используемых снарядов и дорогостоящих методов сбора и проверки данных, что это непрактично для непрофессиональных баллистиков [28] , но не невозможно для любознательных, компьютерно грамотных и математически склонных людей. Были разработаны полуэмпирические модели аэропрогнозирования, которые сократили обширные данные по испытательному диапазону для самых разных форм снарядов, нормализовали размерные входные геометрии до калибров; учитывали длину и радиус носа, длину корпуса и размер хвостовой части и позволяли оценить полный набор аэродинамических коэффициентов с 6 степенями свободы. Ранние исследования программного обеспечения для аэропрогнозирования со стабилизацией вращением привели к созданию компьютерной программы SPINNER. [29] Код аэропрогноза FINNER вычисляет входные данные с 6 степенями свободы для снарядов со стабилизацией плавником. [30] Программное обеспечение для моделирования твердых тел, которое определяет параметры снаряда массы, центра тяжести, осевого и поперечного моментов инерции, необходимые для анализа устойчивости, также легко доступно и просто для компьютерной программы. [31] Наконец, алгоритмы для численного интегрирования с 6 степенями свободы, подходящие для Рунге-Кутты 4-го порядка, легко доступны. [32] Все, что требуется баллистику-любителю для исследования более тонких аналитических деталей траекторий снарядов, а также поведения нутации и прецессии пули , — это определение с помощью компьютерного программирования. Тем не менее, для энтузиаста стрелкового оружия, помимо академического любопытства, можно обнаружить, что возможность предсказывать траектории с точностью с 6 степенями свободы, вероятно, не имеет практического значения по сравнению с более упрощенными траекториями точечной массы, основанными на опубликованных баллистических коэффициентах пуль. 6 DoF обычно используется в аэрокосмической и оборонной промышленности, а также военными организациями, которые изучают баллистическое поведение ограниченного числа (предполагаемых) снарядов военного назначения. Рассчитанные тенденции 6 DoF могут быть включены в качестве таблиц коррекции в более традиционные баллистические программные приложения.
Хотя 6 DoF-моделирование и программные приложения используются профессиональными хорошо оснащенными организациями в течение десятилетий, ограничения вычислительной мощности мобильных вычислительных устройств, таких как (защищенные) персональные цифровые помощники , планшетные компьютеры или смартфоны, затрудняют использование в полевых условиях, поскольку расчеты, как правило, приходится выполнять на лету. В 2016 году скандинавский производитель боеприпасов Nammo Lapua Oy выпустил бесплатное программное обеспечение для расчета 6 DoF, основанное на баллистической модели, под названием Lapua Ballistics. Программное обеспечение распространяется только в виде мобильного приложения и доступно для устройств Android и iOS. [33] Однако используемая 6 DoF-модель ограничена пулями Lapua, поскольку решателю 6 DoF требуются данные о коэффициенте сопротивления пули (Cd)/доплеровском радаре и геометрические размеры интересующего(их) снаряда(ов). Для других пуль решатель Lapua Ballistics ограничен и основан на баллистических коэффициентах G1 или G7 и методе Маевского/Сиаччи.
Программные комплексы для артиллерии
Военные организации разработали баллистические модели, такие как NATO Armament Ballistic Kernel (NABK) для систем управления огнем артиллерии, таких как SG2 Shareable (Fire Control) Software Suite (S4) от NATO Army Armaments Group (NAAG). NATO Armament Ballistic Kernel — это модифицированная точечная массовая модель с 4 степенями свободы. Это компромисс между простой точечной массовой моделью и вычислительно интенсивной 6-степенной моделью. [34] В рабочих группах НАТО также был разработан стандарт с шестью и семью степенями свободы под названием BALCO. BALCO — это программа моделирования траектории, основанная на математической модели, определенной в Рекомендации НАТО по стандартизации 4618. Основной целью BALCO является вычисление высокоточных траекторий как для обычных осесимметричных, так и для высокоточных управляемых снарядов с управляющими поверхностями. Траекторная модель BALCO — это программа на языке FORTRAN 2003, которая реализует следующие функции:
- Уравнения движения с 6/7 степенями свободы
- Интегрирование Рунге-Кутта-Фельберга 7-го порядка.
- Модели Земли
- Модели атмосферы
- Аэродинамические модели
- Модели тяги и базового сгорания
- Модели приводов [35]
Прогнозы, которые дают эти модели, подлежат сравнительному изучению. [36]
Измерения с помощью доплеровского радара
Для точного определения эффектов сопротивления воздуха или сопротивления воздуха на снарядах требуются измерения с помощью доплеровского радара . Доплеровские радары Weibel 1000e или Infinition BR-1001 используются правительствами, профессиональными баллистиками, силами обороны и несколькими производителями боеприпасов для получения реальных данных о поведении интересующих их снарядов в полете. Правильно установленные современные измерения с помощью доплеровского радара могут определять поведение полета снарядов размером с пулю пневматического оружия в трехмерном пространстве с точностью до нескольких миллиметров. Собранные данные о замедлении снаряда могут быть получены и выражены несколькими способами, такими как баллистические коэффициенты (BC) или коэффициенты сопротивления (C d ). Поскольку вращающийся снаряд испытывает как прецессию, так и нутацию вокруг своего центра тяжести во время полета, требуется дальнейшее сокращение данных измерений с помощью доплеровского радара для отделения коэффициентов сопротивления и подъемной силы рыскания от коэффициента сопротивления нулевого рыскания, чтобы сделать измерения полностью применимыми к анализу траектории с 6 степенями свободы.
Результаты измерений с помощью доплеровского радара для выточенной на токарном станке монолитной сплошной пули .50 BMG с очень низким сопротивлением (монолитная сплошная пуля Lost River J40 .510-773 гран / скорость вращения 1:15 дюйма) выглядят следующим образом:
| Диапазон (м) | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | 1300 | 1400 | 1500 | 1600 | 1700 | 1800 | 1900 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Баллистический коэффициент | 1.040 | 1.051 | 1.057 | 1.063 | 1.064 | 1.067 | 1.068 | 1.068 | 1.068 | 1.066 | 1.064 | 1.060 | 1.056 | 1.050 | 1.042 | 1.032 |
Первоначальный рост значения BC объясняется постоянным рысканием снаряда и прецессией из канала ствола. Результаты испытаний были получены из множества выстрелов, а не только из одного. Производитель пули Lost River Ballistic Technologies присвоил пуле номер BC 1,062.
Результаты измерений с помощью доплеровского радара для пули Lapua GB528 Scenar весом 19,44 г (300 гран) и калибром 8,59 мм (0,338 дюйма) с очень низким сопротивлением выглядят следующим образом:
| число Маха | 0.000 | 0.400 | 0.500 | 0.600 | 0.700 | 0.800 | 0,825 | 0,850 | 0,875 | 0.900 | 0,925 | 0.950 | 0,975 | 1.000 | 1.025 | 1.050 | 1.075 | 1.100 | 1.150 | 1.200 | 1.300 | 1.400 | 1.500 | 1.600 | 1.800 | 2.000 | 2.200 | 2.400 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Коэффициент лобового сопротивления | 0.230 | 0,229 | 0.200 | 0,171 | 0,164 | 0,144 | 0,141 | 0,137 | 0,137 | 0,142 | 0,154 | 0,177 | 0,236 | 0,306 | 0.334 | 0,341 | 0,345 | 0,347 | 0,348 | 0,348 | 0,343 | 0,336 | 0,328 | 0,321 | 0,304 | 0,292 | 0,282 | 0.270 |
Максимальный коэффициент лобового сопротивления у этой испытанной пули достигается при выходе на трансзвуковой режим полета со скоростью около 1200 Маха.
С помощью измерений доплеровского радара можно установить модели сопротивления снаряда, которые наиболее полезны при стрельбе на больших расстояниях, где скорость пули замедляется до околозвуковой области скоростей вблизи скорости звука. Именно здесь сопротивление снаряда, предсказанное математическим моделированием, может значительно отличаться от фактического сопротивления, испытываемого снарядом. Дальнейшие измерения доплеровского радара используются для изучения тонких эффектов в полете различных конструкций пуль. [37]
Правительства, профессиональные баллистики, силы обороны и производители боеприпасов могут дополнять измерения доплеровского радара измерениями, полученными с помощью телеметрических зондов, установленных на более крупных снарядах.
Общие тенденции в коэффициенте лобового сопротивления или баллистическом коэффициенте

В общем, заостренный снаряд будет иметь лучший коэффициент сопротивления (C d ) или баллистический коэффициент (BC), чем пуля с круглым носом, а пуля с круглым носом будет иметь лучший C d или BC, чем пуля с плоским носом. Большие радиусы кривизны, приводящие к меньшему углу острия, будут производить меньшее сопротивление, особенно на сверхзвуковых скоростях. Пули с полым носом ведут себя во многом как плоская точка того же диаметра острия. Снаряды, предназначенные для сверхзвукового использования, часто имеют слегка сужающееся основание сзади, называемое хвостовой частью лодки , что снижает сопротивление воздуха в полете. [38] Полезность «сужающейся задней части» для стрельбы на большие расстояния была хорошо известна уже к началу 1870-х годов, [39] но технологические трудности помешали их широкому применению вплоть до начала 20-го века. Каннелюры , которые представляют собой утопленные кольца вокруг снаряда, используемые для надежного обжима снаряда в гильзе, вызовут увеличение сопротивления.
Аналитическое программное обеспечение было разработано Лабораторией баллистических исследований (позже названной Армейской исследовательской лабораторией ), которая свела фактические данные по испытательному диапазону к параметрическим соотношениям для прогнозирования коэффициента сопротивления снаряда. [40] Крупнокалиберная артиллерия также использует механизмы снижения сопротивления в дополнение к обтекаемой геометрии. Ракетные снаряды используют небольшой ракетный двигатель, который воспламеняется при выходе из дула, обеспечивая дополнительную тягу для преодоления аэродинамического сопротивления. Ракетная помощь наиболее эффективна для дозвуковых артиллерийских снарядов. Для сверхзвуковой дальнобойной артиллерии, где доминирует базовое сопротивление, используется донно-выпускное отверстие . Базовое выпускное отверстие представляет собой форму газогенератора, который не обеспечивает значительной тяги, а вместо этого заполняет область низкого давления позади снаряда газом, эффективно снижая базовое сопротивление и общий коэффициент сопротивления снаряда.
Трансзвуковая проблема
Снаряд, выпущенный со сверхзвуковой начальной скоростью, в какой-то момент замедлится, чтобы приблизиться к скорости звука. В околозвуковой области (около 1,2–0,8 Маха ) центр давления (ЦД) большинства несферических снарядов смещается вперед по мере замедления снаряда. Это смещение ЦД влияет на (динамическую) устойчивость снаряда. Если снаряд недостаточно стабилизирован, он не может оставаться направленным вперед через околозвуковую область (снаряд начинает демонстрировать нежелательную прецессию или конусообразное движение, называемое рысканием предельного цикла, которое, если его не демпфировать, может в конечном итоге привести к неконтролируемому кувырку вдоль продольной оси). Однако даже если снаряд имеет достаточную устойчивость (статическую и динамическую), чтобы иметь возможность пролететь через околозвуковую область и оставаться направленным вперед, он все равно подвержен влиянию. Неустойчивое и внезапное смещение ЦД и (временное) снижение динамической устойчивости могут вызвать значительную дисперсию (и, следовательно, значительное снижение точности), даже если полет снаряда снова становится хорошо себя вести, когда он входит в дозвуковую область. Это существенно затрудняет точное прогнозирование баллистического поведения снарядов в околозвуковой области.
Из-за этого стрелки обычно ограничиваются поражением целей, находящихся достаточно близко, чтобы снаряд все еще был сверхзвуковым. [примечание 1] В 2015 году американский баллистик Брайан Литц ввел концепцию «Extended Long Range» для определения стрельбы из винтовки на дистанциях, где сверхзвуковые (винтовочные) пули входят в трансзвуковую область. По словам Литца, «Extended Long Range начинается всякий раз, когда пуля замедляется до своей трансзвуковой области. По мере того, как пуля замедляется до скорости 1 Маха, она начинает сталкиваться с трансзвуковыми эффектами, которые являются более сложными и трудно поддающимися учету по сравнению со сверхзвуковой областью, где пуля ведет себя относительно хорошо». [41]
Плотность окружающего воздуха оказывает значительное влияние на динамическую устойчивость во время трансзвукового перехода. Хотя плотность окружающего воздуха является переменным фактором окружающей среды, неблагоприятные эффекты трансзвукового перехода могут быть лучше нейтрализованы снарядом, движущимся в менее плотном воздухе, чем при движении в более плотном воздухе. Длина снаряда или пули также влияет на рыскание предельного цикла. Более длинные снаряды испытывают большее рыскание предельного цикла, чем более короткие снаряды того же диаметра. Еще одной особенностью конструкции снаряда, которая была идентифицирована как имеющая влияние на нежелательное движение рыскания предельного цикла, является фаска у основания снаряда. У самого основания, или пятки снаряда или пули, имеется фаска от 0,25 до 0,50 мм (от 0,01 до 0,02 дюйма) или радиус. Наличие этого радиуса заставляет снаряд лететь с большими углами рыскания предельного цикла. [42] Нарезка также может оказывать тонкое влияние на рыскание предельного цикла. [43] В целом, более быстрые вращающиеся снаряды испытывают меньшее рыскание предельного цикла.
Исследования в области управляемых снарядов
Чтобы обойти трансзвуковые проблемы, с которыми сталкиваются снаряды со стабилизацией вращением, теоретически снаряды можно направлять во время полета. В январе 2012 года Национальные лаборатории Сандиа объявили, что они исследовали и испытали 4-дюймовые (102 мм) прототипные самонаводящиеся пули, похожие на дротики, для мелкокалиберного гладкоствольного огнестрельного оружия, которые могут поражать цели, обозначенные лазером, на расстоянии более мили (около 1610 метров или 1760 ярдов). Эти снаряды не стабилизированы вращением, и траектория полета может управляться в определенных пределах с помощью электромагнитного привода 30 раз в секунду. Исследователи также утверждают, что у них есть видеозапись того, как пуля радикально отклоняется при выходе из ствола и отклоняется меньше при полете на дальность, спорный феномен, известный экспертам по оружию дальнего действия как «засыпание». Поскольку движения пули успокаиваются с течением времени полета, точность улучшается на больших расстояниях, сказал исследователь Сандиа Ред Джонс. «Никто никогда этого не видел, но у нас есть высокоскоростная видеосъемка, которая показывает, что это правда», — сказал он. [44] Недавние испытания показывают, что он, возможно, приближается или уже достиг начальной эксплуатационной готовности. [45]
Тестирование предсказательных качеств программного обеспечения
Из-за практической невозможности знать заранее и компенсировать все переменные полета, никакое программное моделирование, каким бы продвинутым оно ни было, не даст прогнозов, которые всегда будут идеально соответствовать реальным траекториям. Однако возможно получить прогнозы, которые очень близки к реальному поведению полета.
Эмпирический метод измерения
Программы компьютерного баллистического прогнозирования, предназначенные для (экстремально) больших дальностей, можно оценить, проведя полевые испытания на сверхзвуковом переходном диапазоне (последние 10–20% сверхзвукового диапазона комбинации винтовка/патрон/пуля). Например, для типичной винтовки .338 Lapua Magnum, стреляющей стандартными пулями Lapua Scenar GB488 весом 16,2 грамма (250 гран) с начальной скоростью 905 м/с (2969 футов/с), полевые испытания программного обеспечения должны проводиться на расстоянии ≈ 1200–1300 метров (1312–1422 ярда) в условиях Международной стандартной атмосферы на уровне моря ( плотность воздуха ρ = 1,225 кг/м³). Чтобы проверить, насколько хорошо программное обеспечение предсказывает траекторию на коротких и средних дистанциях, необходимо провести полевые испытания на 20, 40 и 60% сверхзвукового диапазона. На этих более коротких и средних дистанциях трансзвуковые проблемы и, следовательно, неконтролируемый полет пули не должны возникать, а BC менее вероятно будет временным. Тестирование предсказательных качеств программного обеспечения на (экстремально) больших дистанциях обходится дорого, поскольку оно потребляет боеприпасы; фактическая начальная скорость всех произведенных выстрелов должна быть измерена, чтобы иметь возможность делать статистически надежные заявления. Группы выборки менее 24 выстрелов могут не получить желаемый статистически значимый доверительный интервал .
Метод измерения с помощью доплеровского радара
Правительства, профессиональные баллистики, силы обороны и несколько производителей боеприпасов используют доплеровские радары и/или телеметрические зонды, установленные на более крупных снарядах, чтобы получить точные данные о реальном мире относительно поведения полета конкретных интересующих их снарядов, а затем сравнить собранные данные о реальном мире с прогнозами, рассчитанными баллистическими компьютерными программами. Однако обычный энтузиаст стрельбы или аэродинамики не имеет доступа к таким дорогим профессиональным измерительным приборам. Органы власти и производители снарядов, как правило, неохотно делятся результатами испытаний доплеровских радаров и полученными в ходе испытаний коэффициентами сопротивления (C d ) снарядов с широкой публикой. Около 2020 года для широкой публики стало доступно более доступное, но менее эффективное (любительское) доплеровское радарное оборудование для определения коэффициентов сопротивления свободного полета. [46]
В январе 2009 года скандинавский производитель боеприпасов Nammo/Lapua опубликовал данные о коэффициенте сопротивления, полученные с помощью доплеровского радара, для большинства своих винтовочных снарядов. [47] [48] В 2015 году американский производитель боеприпасов Berger Bullets объявил об использовании доплеровского радара совместно с программным обеспечением PRODAS 6 DoF для генерации решений по траектории. [49] В 2016 году американский производитель боеприпасов Hornady объявил об использовании данных о сопротивлении, полученных с помощью доплеровского радара, в программном обеспечении, использующем модифицированную модель точечной массы для генерации решений по траектории. [50] [51] [52] [53] С помощью полученных с помощью измерений данных C d инженеры могут создавать алгоритмы, которые используют как известные математические баллистические модели, так и специальные табличные данные для испытаний одновременно. При использовании прогностического программного обеспечения, такого как QuickTARGET Unlimited , Lapua Edition, [54] Lapua Ballistics [55] или Hornady 4DOF, данные о коэффициенте сопротивления, полученные с помощью доплеровского радара, можно использовать для более точных внешнебаллистических прогнозов.
Некоторые из предоставленных Lapua данных о коэффициенте сопротивления показывают резкое увеличение измеренного сопротивления около или ниже области скорости полета Маха 1. Такое поведение наблюдалось для большинства измеренных пуль малого калибра и не так сильно для пуль большего калибра. Это означает, что некоторые (в основном меньшего калибра) винтовочные пули демонстрировали большее рыскание предельного цикла (конусность и/или кувыркание) в режиме околозвуковой/дозвуковой скорости полета. Информация о неблагоприятном поведении околозвукового/дозвукового полета для некоторых из испытанных снарядов важна. Это ограничивающий фактор для использования стрельбы на большие дальности, поскольку эффекты рыскания предельного цикла нелегко предсказать и потенциально катастрофичны для лучших моделей и программного обеспечения баллистического прогнозирования.
Представленные данные C d не могут быть просто использованы для каждой комбинации оружия и боеприпасов, поскольку они были измерены для стволов, скоростей вращения (спин) и партий боеприпасов, которые испытатели Lapua использовали во время своих испытательных стрельб. Такие переменные, как различия в нарезах (количество канавок, глубина, ширина и другие размерные свойства), скорости закручивания и/или начальные скорости придают снарядам разные скорости вращения (спин) и следы нарезов. Изменения таких переменных и вариации партий производства снарядов могут привести к различному взаимодействию на дальности с воздухом, через который проходит снаряд, что может привести к (незначительным) изменениям в поведении полета. Эта конкретная область внешней баллистики в настоящее время (2009) не изучена подробно и не понята. [56]
Прогнозы нескольких методов моделирования и измерения сопротивления движению
Метод, используемый для моделирования и прогнозирования внешнего баллистического поведения, может давать разные результаты с увеличением дальности и времени полета. Чтобы проиллюстрировать это, несколько методов прогнозирования внешнего баллистического поведения для винтовочной пули Lapua Scenar GB528 19,44 г (300 г) калибра 8,59 мм (0,338 дюйма) с очень низким сопротивлением с заявленным производителем баллистическим коэффициентом G1 (BC) 0,785, выпущенной с начальной скоростью 830 м/с (2723 фута/с) в условиях международной стандартной атмосферы на уровне моря ( плотность воздуха ρ = 1,225 кг/м³), Маха 1 = 340,3 м/с, Маха 1,2 = 408,4 м/с), предсказали это для скорости снаряда и времени полета от 0 до 3000 м (от 0 до 3281 ярда): [примечание 2]
| Диапазон (м) | 0 | 300 | 600 | 900 | 1200 | 1500 | 1,800 | 2,100 | 2400 | 2,700 | 3000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Метод определения коэффициентов сопротивления, полученных с помощью радиолокационного испытания V (м/с) | 830 | 711 | 604 | 507 | 422 | 349 | 311 | 288 | 267 | 247 | 227 |
| Время полета (с) | 0.0000 | 0,3918 | 0,8507 | 1.3937 | 2.0435 | 2.8276 | 3.7480 | 4.7522 | 5.8354 | 7.0095 | 8.2909 |
| Общее падение (м) | 0.000 | 0,715 | 3.203 | 8.146 | 16.571 | 30.035 | 50.715 | 80.529 | 121.023 | 173.998 | 241.735 |
| 6 Метод моделирования DoF V (м/с) | 830 | 711 | 604 | 506 | 420 | 347 | 310 | 287 | 266 | 244 | 222 |
| Время полета (с) | 0.0000 | 0,3919 | 0,8511 | 1.3949 | 2.0467 | 2.8343 | 3.7575 | 4.7641 | 5.8508 | 7.0332 | 8.3346 |
| Общее падение (м) | 0.000 | 0,714 | 3.195 | 8.132 | 16.561 | 30.060 | 50.836 | 80.794 | 121.498 | 174.796 | 243.191 |
| Метод модели сопротивления G1 V (м/с) | 830 | 718 | 615 | 522 | 440 | 374 | 328 | 299 | 278 | 261 | 248 |
| Время полета (с) | 0.0000 | 0,3897 | 0,8423 | 1.3732 | 2.0009 | 2.7427 | 3.6029 | 4.5642 | 5.6086 | 6.7276 | 7.9183 |
| Общее падение (м) | 0.000 | 0,710 | 3.157 | 7.971 | 16.073 | 28.779 | 47.810 | 75.205 | 112.136 | 160.739 | 222.430 |
| Метод модели сопротивления Пейсы V (м/с) | 830 | 712 | 603 | 504 | 413 | 339 | 297 | 270 | 247 | 227 | 208 |
| Время полета (с) | 0.0000 | 0,3902 | 0,8479 | 1.3921 | 2.0501 | 2.8556 | 3.8057 | 4.8682 | 6.0294 | 7.2958 | 8.6769 |
| Общее падение (м) | 0.000 | 0,719 | 3.198 | 8.129 | 16.580 | 30.271 | 51.582 | 82.873 | 126.870 | 185.318 | 260.968 |
| Метод модели сопротивления G7 V (м/с) | 830 | 713 | 606 | 508 | 418 | 339 | 303 | 283 | 265 | 249 | 235 |
| Время полета (с) | 0.0000 | 0,3912 | 0,8487 | 1.3901 | 2.0415 | 2.8404 | 3.7850 | 4.8110 | 5.9099 | 7.0838 | 8.3369 |
| Общее падение (м) | 0.000 | 0,714 | 3.191 | 8.109 | 16.503 | 30.039 | 51.165 | 81.863 | 123.639 | 178.082 | 246.968 |
Таблица показывает, что метод прогнозирования коэффициентов сопротивления, полученных с помощью доплеровского радара (C d ), и прогнозы приложения Lapua Ballistics 6 DoF App 2017 года дают схожие результаты. Моделирование 6 DoF оценивает устойчивость пули ((S d ) и (S g )), которая тяготеет к чрезмерной стабилизации на дальностях более 2400 м (2625 ярдов) для этой пули. На расстоянии 2400 м (2625 ярдов) общие прогнозы падения отклоняются на 47,5 см (19,7 дюйма) или 0,20 мил (0,68 моа ) на широте 50°, а до 2700 м (2953 ярда) общие прогнозы падения находятся в пределах 0,30 мил (1 моа) на широте 50°. Прогнозы версии приложения Lapua Ballistics 6 DoF 2016 года оказались еще ближе к прогнозам, полученным в ходе испытаний радара Доплера.
Традиционный метод прогнозирования кривой сопротивления Siacci/Mayevski G1 обычно дает более оптимистичные результаты по сравнению с современным методом прогнозирования коэффициентов сопротивления (C d ), полученных с помощью доплеровского радара. [примечание 3] На расстоянии 300 м (328 ярдов) различия будут едва заметны, но на расстоянии 600 м (656 ярдов) и далее различия увеличиваются более чем на 10 м/с (32,8 фут/с) скорости снаряда и постепенно становятся значительными. На расстоянии 1500 м (1640 ярдов) прогнозы скорости снаряда отклоняются на 25 м/с (82,0 фут/с), что соответствует прогнозируемой разнице общего падения в 125,6 см (49,4 дюйма) или 0,83 мил (2,87 МОА) на широте 50°.
Метод прогнозирования решения замкнутой формы модели сопротивления Пейсы без тонкой настройки постоянного коэффициента наклона дает очень похожие результаты в сверхзвуковом режиме полета по сравнению с методом прогнозирования коэффициентов сопротивления, полученных с помощью теста Доплеровского радара (C d ). На расстоянии 1500 м (1640 ярдов) прогнозы скорости снаряда отклоняются на 10 м/с (32,8 фута/с), что соответствует прогнозируемой разнице общего падения в 23,6 см (9,3 дюйма) или 0,16 мил (0,54 моа) на широте 50°.
Метод прогнозирования модели кривой сопротивления G7 (рекомендуемый некоторыми производителями для винтовочных пуль с очень низким сопротивлением) при использовании баллистического коэффициента G7 (BC) 0,377 дает очень похожие результаты в сверхзвуковом режиме полета по сравнению с методом прогнозирования коэффициентов сопротивления, полученных с помощью доплеровского радара (C d ). На расстоянии 1500 м (1640 ярдов) прогнозы скорости снаряда имеют максимальное отклонение 10 м/с (32,8 фута/с). Прогнозируемая общая разница падения на 1500 м (1640 ярдов) составляет 0,4 см (0,16 дюйма) на широте 50°. Прогнозируемая общая разница падения на 1800 м (1969 ярдов) составляет 45,0 см (17,7 дюйма), что соответствует 0,25 мил (0,86 moa).
Ожидается, что достойные модели прогнозирования дадут схожие результаты в сверхзвуковом режиме полета. Пять примеров моделей до 1200 м (1312 ярдов) все предсказывают сверхзвуковые скорости снаряда 1,2 Маха + и общую разницу падения в пределах полосы пропускания 51 см (20,1 дюйма). В околозвуковом режиме полета на высоте 1500 м (1640 ярдов) модели предсказывают скорости снаряда около 1,0 Маха до 1,1 Маха и общую разницу падения в пределах гораздо большей полосы пропускания 150 см (59 дюймов).
Внешние факторы
Ветер
Ветер имеет ряд эффектов, первый из которых заключается в отклонении снаряда в сторону (горизонтальное отклонение). С научной точки зрения, «ветер, толкающий снаряд в сторону» не является причиной горизонтального ветрового сноса. Причиной ветрового сноса является сопротивление. Сопротивление заставляет снаряд поворачиваться по ветру, подобно флюгеру, удерживая центр давления воздуха на его носу. С точки зрения стрелка, это заставляет нос снаряда поворачиваться по ветру, а хвост — от ветра. Результатом этого эффекта поворота является то, что сопротивление толкает снаряд по ветру в направлении от носа к хвосту.
Ветер также вызывает аэродинамический скачок, который является вертикальной составляющей отклонения поперечного ветра, вызванного боковыми (ветровыми) импульсами, активируемыми во время свободного полета снаряда или на дульном срезе или очень близко к нему, что приводит к динамическому дисбалансу. [57] Величина аэродинамического скачка зависит от скорости поперечного ветра, гироскопической устойчивости пули на дульном срезе и от того, закручен ствол по часовой стрелке или против часовой стрелки. Подобно направлению ветра, изменение направления закрученности изменит направление аэродинамического скачка.
Несколько менее очевидный эффект вызывает встречный или попутный ветер. Встречный ветер немного увеличит относительную скорость снаряда и увеличит сопротивление и соответствующее падение. Попутный ветер уменьшит сопротивление и падение снаряда/пули. В реальном мире чистый встречный или попутный ветер встречается редко, поскольку ветер редко бывает постоянным по силе и направлению и обычно взаимодействует с местностью, над которой он дует. Это часто затрудняет стрельбу на сверхдальние дистанции в условиях встречного или попутного ветра.
Вертикальные углы
Вертикальный угол (или возвышение ) выстрела также повлияет на траекторию выстрела. Баллистические таблицы для малокалиберных снарядов (выстреливаемых из пистолетов или винтовок) предполагают горизонтальную линию визирования между стрелком и целью с силой тяжести, действующей перпендикулярно земле. Следовательно, если угол между стрелком и целью направлен вверх или вниз (направление компонента силы тяжести не меняется с направлением наклона), то ускорение искривления траектории под действием силы тяжести будет фактически меньше, пропорционально косинусу угла наклона. В результате снаряд, выпущенный вверх или вниз, на так называемой «наклонной дальности», пролетит мимо той же целевой дистанции на ровной поверхности. Эффект достаточно велик, чтобы охотники должны соответствующим образом корректировать удержание цели в горной местности. Хорошо известная формула для корректировки наклонной дальности до горизонтальной дальности известна как правило стрелка . Правило стрелка и немного более сложные и менее известные модели улучшенного правила стрелка дают достаточно точные прогнозы для многих применений стрелкового оружия. Однако простые модели прогнозирования игнорируют незначительные эффекты гравитации при стрельбе вверх или вниз по склону. Единственный практический способ компенсировать это — использовать баллистическую компьютерную программу. Помимо гравитации под очень крутыми углами на больших расстояниях, влияние изменения плотности воздуха, с которым сталкивается снаряд во время полета, становится проблематичным. [58] Математические модели прогнозирования, доступные для сценариев наклонного огня, в зависимости от величины и направления (вверх или вниз) угла наклона и дальности, дают различные уровни ожиданий точности. [59] Менее продвинутые баллистические компьютерные программы предсказывают одну и ту же траекторию для выстрелов вверх и вниз по склону при одном и том же вертикальном угле и дальности. Более продвинутые программы учитывают небольшое влияние гравитации на выстрелы вверх и вниз по склону, что приводит к немного отличающимся траекториям при одном и том же вертикальном угле и дальности. В настоящее время (2017 г.) ни одна общедоступная баллистическая компьютерная программа не учитывает сложные явления различной плотности воздуха, с которыми сталкивается снаряд во время полета.
Плотность окружающего воздуха
Давление воздуха , температура и колебания влажности составляют плотность окружающего воздуха . Влажность оказывает противоестественное воздействие. Поскольку плотность водяного пара составляет 0,8 грамма на литр, а средняя плотность сухого воздуха составляет около 1,225 грамма на литр, более высокая влажность фактически снижает плотность воздуха и, следовательно, уменьшает сопротивление.
Осадки
Осадки могут вызвать значительное рыскание и сопутствующее отклонение, когда пуля сталкивается с каплей дождя. Чем дальше вниз по дальности происходит такое случайное столкновение, тем меньше будет отклонение на цели. Вес капли дождя и пули также влияет на то, насколько сильно рыскание будет вызвано во время такого столкновения. Большая тяжелая капля дождя и легкая пуля дадут максимальный эффект рыскания. Тяжелая пуля, сталкивающаяся с такой же каплей дождя, испытает значительно меньший эффект рыскания. [60]
Факторы дальнего действия
Гироскопический дрейф (спиновый дрейф)
Гироскопический дрейф — это взаимодействие массы и аэродинамики пули с атмосферой, в которой она летит. Даже в совершенно спокойном воздухе, при полном отсутствии бокового движения воздуха, стабилизированный вращением снаряд будет испытывать вызванную вращением боковую составляющую из-за гироскопического явления, известного как «рыскание покоя». Для правого (по часовой стрелке) направления вращения этот компонент всегда будет справа. Для левого (против часовой стрелки) направления вращения этот компонент всегда будет слева. Это происходит потому, что продольная ось снаряда (его ось вращения) и направление вектора скорости центра тяжести (ЦТ) отклоняются на небольшой угол, который называется равновесным рысканием или рысканием покоя. Величина угла рыскания покоя обычно меньше 0,5 градуса. [61] Поскольку вращающиеся объекты реагируют с вектором угловой скорости, составляющим 90 градусов от приложенного вектора крутящего момента, ось симметрии пули движется с компонентой в вертикальной плоскости и компонентой в горизонтальной плоскости; для правосторонних (по часовой стрелке) вращающихся пуль ось симметрии пули отклоняется вправо и немного вверх относительно направления вектора скорости, когда снаряд движется по своей баллистической дуге. В результате этого небольшого наклона возникает непрерывный поток воздуха, который стремится отклонить пулю вправо. Таким образом, возникновение рыскания покоя является причиной дрейфа пули вправо (для правостороннего вращения) или влево (для левостороннего вращения). Это означает, что пуля «скользит» вбок в любой момент и, таким образом, испытывает боковую составляющую. [62] [63]
На величину гироскопического дрейфа влияют следующие переменные:
- Длина снаряда или пули: более длинные снаряды испытывают больший гироскопический дрейф, поскольку они создают большую боковую «подъемную силу» для заданного угла рыскания.
- Скорость вращения: более высокая скорость вращения приведет к большему гироскопическому дрейфу, поскольку нос будет направлен дальше в сторону.
- Дальность, время полета и высота траектории: гироскопический дрейф увеличивается с увеличением всех этих переменных.
- Плотность атмосферы: более плотный воздух увеличит гироскопический дрейф.
Результаты измерений с помощью доплеровского радара гироскопического дрейфа нескольких американских пуль военного и другого назначения с очень низким сопротивлением на расстоянии 1000 ярдов (914,4 м) выглядят следующим образом:
| Тип пули | Американский военный M193 Ball (5,56×45 мм НАТО) | Американский военный M118 Special Ball (7,62×51 мм НАТО) | Пальма Сьерра MatchKing | LRBT J40 матч | Sierra MatchKing | Sierra MatchKing | LRBT J40 матч | LRBT J40 матч |
|---|---|---|---|---|---|---|---|---|
| Масса снаряда (в гранах и г) | 55 гран (3,56 г) | 173 грана (11,21 г) | 155 гран (10,04 г) | 190 гран (12,31 г) | 220 гран (14,26 г) | 300 гран (19,44 г) | 350 гран (22,68 г) | 419 гран (27,15 г) |
| Диаметр снаряда (в дюймах и мм) | .224 дюйма (5,69 мм) | .308 дюйма (7,82 мм) | .308 дюйма (7,82 мм) | .308 дюйма (7,82 мм) | .308 дюйма (7,82 мм) | .338 дюйма (8,59 мм) | .375 дюйма (9,53 мм) | .408 дюйма (10,36 мм) |
| Гироскопический дрейф (в дюймах и мм) | 23,00 дюйма (584,20 мм) | 11,50 дюймов (292,10 мм) | 12,75 дюйма (323,85 мм) | 3,00 дюйма (76,20 мм) | 7,75 дюйма (196,85 мм) | 6,50 дюймов (165,10 мм) | 0,87 дюйма (22,10 мм) | 1,90 дюйма (48,26 мм) |
Таблица показывает, что гироскопический дрейф нельзя предсказать только по весу и диаметру. Для того чтобы сделать точные прогнозы по гироскопическому дрейфу, необходимо учитывать несколько деталей как внешней, так и внутренней баллистики. Такие факторы, как скорость поворота ствола, скорость снаряда при выходе из дула, гармоники ствола и атмосферные условия, влияют на траекторию снаряда.
эффект Магнуса
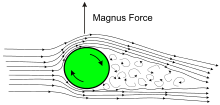
Снаряды, стабилизированные вращением, подвержены эффекту Магнуса , при котором вращение пули создает силу, действующую либо вверх, либо вниз, перпендикулярно боковому вектору ветра. В простом случае горизонтального ветра и правого (по часовой стрелке) направления вращения эффект Магнуса, вызванный разницей давления вокруг пули, вызывает направленную вниз (ветер справа) или вверх (ветер слева) силу, рассматриваемую с точки выстрела, чтобы воздействовать на снаряд, влияя на его точку попадания. [64] Значение вертикального отклонения, как правило, мало по сравнению с компонентом отклонения, вызванным горизонтальным ветром, но тем не менее оно может быть значительным при ветре, превышающем 4 м/с (14,4 км/ч или 9 миль/ч).
Эффект Магнуса и стабильность пули
Эффект Магнуса играет важную роль в устойчивости пули, поскольку сила Магнуса действует не на центр тяжести пули, а на центр давления, влияющий на рыскание пули. Эффект Магнуса будет действовать как дестабилизирующая сила на любую пулю с центром давления, расположенным впереди центра тяжести, и наоборот, как стабилизирующая сила на любую пулю с центром давления, расположенным позади центра тяжести. Расположение центра давления зависит от структуры поля потока, другими словами, от того, летит ли пуля сверхзвуковым, околозвуковым или дозвуковым способом. Что это означает на практике, зависит от формы и других характеристик пули, в любом случае сила Магнуса сильно влияет на устойчивость, поскольку она пытается «закрутить» пулю вдоль ее траектории полета. [65] [66]
Парадоксально, но пули с очень низким сопротивлением из -за своей длины имеют тенденцию демонстрировать большие ошибки дестабилизации Магнуса, поскольку они имеют большую площадь поверхности, чтобы представить набегающему воздуху, через который они летят, тем самым снижая свою аэродинамическую эффективность. Этот тонкий эффект является одной из причин, по которой вычисленный C d или BC на основе формы и плотности сечения имеет ограниченное применение.
эффект Пуассона
Другая второстепенная причина дрейфа, которая зависит от того, что нос снаряда находится выше траектории, — это эффект Пуассона. Он, если он вообще имеет место, действует в том же направлении, что и гироскопический дрейф, и даже менее важен, чем эффект Магнуса. Он предполагает, что загнутый вверх нос снаряда заставляет под собой образовываться воздушную подушку. Он также предполагает, что между этой подушкой и снарядом увеличивается трение, так что последний, вращаясь, будет стремиться скатиться с подушки и двигаться вбок.
Это простое объяснение довольно популярно. Однако нет никаких доказательств того, что повышенное давление означает повышенное трение, и если это не так, то не может быть никакого эффекта. Даже если он существует, он должен быть совершенно незначительным по сравнению с гироскопическим и кориолисовым дрейфами.
Оба эффекта Пуассона и Магнуса изменят направление дрейфа, если нос опустится ниже траектории. Когда нос смещен в сторону, как при равновесном рыскании, эти эффекты будут вносить незначительные изменения в диапазон.
Кориолисов дрейф
Эффект Кориолиса вызывает дрейф Кориолиса в направлении, перпендикулярном оси Земли; для большинства местоположений на Земле и направлений стрельбы это отклонение включает горизонтальные и вертикальные компоненты. Отклонение происходит справа от траектории в северном полушарии, слева в южном полушарии, вверх для выстрелов в восточном направлении и вниз для выстрелов в западном направлении. Вертикальное отклонение Кориолиса также известно как эффект Этвеша . Дрейф Кориолиса не является аэродинамическим эффектом; он является следствием вращения Земли.
Величина эффекта Кориолиса мала. Для стрелкового оружия величина эффекта Кориолиса, как правило, незначительна (для мощных винтовок порядка 10 см (3,9 дюйма) на 1000 м (1094 ярда)), но для баллистических снарядов с большим временем полета, таких как сверхдальние винтовочные снаряды, артиллерия и ракеты, такие как межконтинентальные баллистические ракеты , это существенный фактор при расчете траектории. Величина дрейфа зависит от места стрельбы и цели, азимута стрельбы, скорости снаряда и времени полета.
Горизонтальный эффект
Если смотреть из невращающейся системы отсчета (т. е. не вращающейся вместе с Землей) и игнорировать силы гравитации и сопротивления воздуха, снаряд движется по прямой линии. Если смотреть из системы отсчета, зафиксированной относительно Земли, эта прямая траектория кажется искривленной вбок. Направление этой горизонтальной кривизны направлено вправо в северном полушарии и влево в южном полушарии и не зависит от азимута выстрела. Горизонтальная кривизна имеет наибольшую величину на полюсах и уменьшается до нуля на экваторе. [67]
Вертикальный (Этвешский) эффект
Эффект Этвеша изменяет воспринимаемое гравитационное притяжение движущегося объекта на основе взаимосвязи между направлением и скоростью движения и направлением вращения Земли. [68] [69]
Эффект Этвеша сильнее всего на экваторе и уменьшается до нуля на полюсах. Он заставляет движущиеся на восток снаряды отклоняться вверх, а движущиеся на запад снаряды отклоняться вниз. Эффект менее выражен для траекторий в других направлениях и равен нулю для траекторий, направленных строго на север или юг. В случае больших изменений импульса, таких как запуск космического корабля на орбиту Земли, эффект становится значительным. Он способствует самому быстрому и экономичному пути к орбите: запуск с экватора, который изгибается в направлении прямо на восток.
Факторы оборудования
Хотя это и не силы, действующие на траектории снарядов, есть некоторые факторы, связанные с оборудованием, которые влияют на траектории. Поскольку эти факторы могут вызывать иначе необъяснимое внешнее баллистическое поведение полета, их следует кратко упомянуть.
Боковой прыжок
Боковой скачок вызван небольшим боковым и вращательным движением ствола оружия в момент выстрела. Он имеет эффект небольшой ошибки пеленга. Эффект игнорируется, так как он мал и меняется от выстрела к выстрелу.
Боковой бросок
Боковой выброс вызван дисбалансом масс в применяемых стабилизированных вращением снарядах или дисбалансом давления во время переходной фазы полета , когда снаряд покидает ствол орудия вне оси, что приводит к статическому дисбалансу. Если он присутствует, он вызывает рассеивание. Эффект непредсказуем, так как он, как правило, невелик и варьируется от снаряда к снаряду, от снаряда к снаряду и/или от ствола к стволу.
Максимальная эффективная дальность стрельбы из стрелкового оружия
Максимальная практическая дальность [примечание 4] всего стрелкового оружия и особенно мощных снайперских винтовок зависит в основном от аэродинамической или баллистической эффективности используемых стабилизированных вращением снарядов. Стрелки на дальние дистанции также должны собирать соответствующую информацию для расчета поправок на возвышение и ветер, чтобы иметь возможность поражать точечные цели с первого выстрела. Данные для расчета этих поправок на управление огнем имеют длинный список переменных, включая: [70]
- баллистический коэффициент или коэффициент сопротивления, полученный в результате испытаний (Cd)/поведение используемых пуль
- высота прицельных приспособлений над осью канала ствола
- нулевая дальность, на которой пристреливались прицельные элементы и винтовочная комбинация
- масса пули
- фактическая начальная скорость пули (температура пороха влияет на начальную скорость пули, воспламенение капсюля также зависит от температуры)
- диапазон до цели
- сверхзвуковая дальность стрельбы используемой комбинации оружия, патрона и пули
- Угол наклона при стрельбе вверх/вниз
- целевая скорость и направление
- Скорость и направление ветра (основная причина горизонтального отклонения снаряда и, как правило, самая сложная баллистическая переменная для правильного измерения и оценки. Влияние ветра также может вызывать вертикальное отклонение.)
- изменения давления воздуха , температуры , высоты и влажности (они составляют плотность окружающего воздуха )
- Гравитация Земли (немного меняется в зависимости от широты и высоты )
- гироскопический дрейф (гироскопический эффект в горизонтальной и вертикальной плоскости — часто называемый спиновым дрейфом — вызванный направлением и скоростью закручивания ствола)
- Дрейф под действием эффекта Кориолиса ( данные о широте , направлении огня и северном или южном полушарии определяют этот эффект)
- Эффект Этвеша (взаимосвязан с эффектом Кориолиса, этот эффект определяется широтой и направлением огня)
- аэродинамический скачок (вертикальная составляющая отклонения поперечного ветра, вызванная боковыми (ветровыми) импульсами, активируемыми во время свободного полета или на уровне или очень близко к дульному срезу, что приводит к динамическому дисбалансу) [57]
- боковой разброс (рассеивание, вызванное дисбалансом массы в применяемом снаряде или его отклонением от оси ствола, что приводит к статическому дисбалансу)
- потенциальная точность и диапазон регулировки прицельных элементов
- присущая винтовке потенциальная точность
- присущая потенциальная точность боеприпасов
- внутренняя потенциальная точность компьютерной программы и других компонентов управления стрельбой, используемых для расчета траектории
Плотность окружающего воздуха максимальна в условиях арктического уровня моря. Холодный порох также создает более низкое давление и, следовательно, более низкую начальную скорость, чем теплый порох. Это означает, что максимальная практическая дальность стрельбы винтовок будет наименьшей в условиях арктического уровня моря.
Способность поражать точечную цель на большом расстоянии во многом зависит от способности справляться с экологическими и метеорологическими факторами, а также от хорошего понимания внешней баллистики и ограничений оборудования. Без (компьютерной) поддержки и высокоточных лазерных дальномеров и метеорологического измерительного оборудования в качестве вспомогательных средств для определения баллистических решений стрельба на большие расстояния за пределами 1000 м (1100 ярдов) на неизвестных расстояниях становится догадкой даже для самых опытных дальнобойщиков. [примечание 5]
Интересное дополнительное чтение: Вики-книга по меткой стрельбе
Использование баллистических данных
Вот пример баллистической таблицы для пули Speer калибра .30 с заостренным хвостом и лодочным сужением массой 169 гран (11 г) с БК 0,480. Она предполагает, что прицел находится на расстоянии 1,5 дюйма (38 мм) над линией канала ствола, а прицел отрегулирован так, чтобы точка прицеливания и точка попадания совпадали на расстоянии 200 ярдов (183 м) и 300 ярдов (274 м) соответственно.
| Диапазон | 0 | 100 ярдов 91 м | 200 ярдов 183 м | 300 ярдов 274 м | 400 ярдов 366 м | 500 ярдов 457 м | |
|---|---|---|---|---|---|---|---|
| Скорость | ( фут/с ) | 2,700 | 2,512 | 2,331 | 2,158 | 1,992 | 1,834 |
| ( РС ) | 823 | 766 | 710 | 658 | 607 | 559 | |
| Пристрелян на 200 ярдов/184 м | |||||||
| Высота | (в) | −1,5 | 2.0 | 0 | −8,4 | −24,3 | −49,0 |
| (мм) | −38 | 51 | 0 | −213 | −617 | −1245 | |
| Пристрелян на 300 ярдов/274 м | |||||||
| Высота | (в) | −1,5 | 4.8 | 5.6 | 0 | −13,1 | −35,0 |
| (мм) | −38 | 122 | 142 | 0 | −333 | −889 | |
Эта таблица показывает, что даже при довольно аэродинамической пуле, выпущенной с высокой скоростью, «падение пули» или изменение точки попадания является значительным. Это изменение точки попадания имеет два важных последствия. Во-первых, оценка расстояния до цели имеет решающее значение на больших дистанциях, потому что разница в точке попадания между 400 и 500 ярдами (460 м) составляет 25–32 дюйма (в зависимости от нуля), другими словами, если стрелок оценивает, что цель находится на расстоянии 400 ярдов, когда на самом деле она находится на расстоянии 500 ярдов, выстрел попадет на 25–32 дюйма (635–813 мм) ниже того места, куда он был нацелен, возможно, полностью промахнувшись мимо цели. Во-вторых, винтовка должна быть обнулена на расстоянии, соответствующем типичному диапазону целей, потому что стрелку, возможно, придется целиться настолько выше цели, чтобы компенсировать большое падение пули, что он может полностью потерять цель из виду (например, находясь вне поля зрения оптического прицела). В примере с винтовкой, пристрелянной на 200 ярдов (180 м), стрелку придется целиться на 49 дюймов или более чем на 4 фута (1,2 м) выше точки попадания для цели на расстоянии 500 ярдов.
Смотрите также
- Внутренняя баллистика — поведение снаряда и пороха до того, как они покинут ствол.
- Переходная баллистика — поведение снаряда с момента вылета из дула до выравнивания давления позади снаряда.
- Терминальная баллистика — поведение снаряда при ударе о цель.
- Траектория снаряда - Основные математические формулы внешней баллистики.
- Правило стрелка — процедуры или «правила» для стрелка по прицеливанию по целям на расстоянии, как вверх, так и вниз по склону.
- Франклин Уэр Манн — Ранние научные исследования внешней баллистики.
- Таблица патронов для пистолетов и винтовок
- Прицеливание — калибровка прицела на дальнобойном оружии таким образом, чтобы точка прицеливания пересекалась с траекторией на заданном расстоянии, что позволяет пользователю стабильно поражать цель, на которую направлен выстрел.
Примечания
- ^ Большинство стабилизируемых вращением снарядов, страдающих от недостатка динамической устойчивости, имеют проблему вблизи скорости звука, где аэродинамические силы и моменты демонстрируют большие изменения. Менее распространено (но возможно) для пуль проявлять значительный недостаток динамической устойчивости на сверхзвуковых скоростях. Поскольку динамическая устойчивость в основном регулируется трансзвуковой аэродинамикой, очень трудно предсказать, когда снаряд будет иметь достаточную динамическую устойчивость (это самые сложные аэродинамические коэффициенты для точного расчета в самом сложном для прогнозирования скоростном режиме (трансзвуковом)). Аэродинамические коэффициенты, которые управляют динамической устойчивостью: момент тангажа, момент Магнуса и сумма коэффициента динамического момента тангажа и угла атаки (очень сложная для прогнозирования величина). В конце концов, моделирование и имитация мало что могут сделать для точного прогнозирования уровня динамической устойчивости, который будет иметь пуля на дальности. Если снаряд имеет очень высокий или низкий уровень динамической устойчивости, моделирование может дать правильный ответ. Однако, если ситуация пограничная (динамическая устойчивость около 0 или 2), моделирование не может быть использовано для получения правильного ответа. Это одна из тех вещей, которые должны быть проверены в полевых условиях и тщательно документированы.
- ^ Метод прогнозирования коэффициентов сопротивления (C d ), полученных с помощью тестов G1, G7 и доплеровского радара, рассчитан с помощью QuickTARGET Unlimited, Lapua Edition. Прогнозы Pejsa, рассчитанные с помощью баллистического программного обеспечения Lex Talus Corporation Pejsa с постоянным коэффициентом наклона, установленным на значение по умолчанию 0,5. Прогнозы моделирования 6 DoF, рассчитанные с помощью приложения Lapua Ballistics 1.0 для Android.
- ^ Данные C d используются инженерами для создания алгоритмов, которые используют как известные математические баллистические модели, так и специальные табличные данные для тестирования в унисон, чтобы получать прогнозы, очень близкие к реальному поведению в полете.
- ^ Снайперская стрельба Архивировано 2007-11-07 на сайте Wayback Machine определяет эффективную дальность как: дальность, на которой компетентный и обученный человек, использующий огнестрельное оружие, имеет возможность поразить цель в шестидесяти-восьмидесяти процентах случаев. В действительности, большинство огнестрельного оружия имеют истинную дальность, намного большую, чем эта, но вероятность поражения цели невелика на дальности, большей эффективной. Кажется, не существует хорошей формулы для эффективной дальности для различных видов огнестрельного оружия.
- ^ Пример того, насколько точно стрелок на дальние дистанции должен установить параметры прицеливания для расчета правильного баллистического решения, объясняется этими результатами тестовых выстрелов. Винтовка .338 Lapua Magnum, пристрелянная на 300 м, стреляла пулями Lapua Scenar весом 250 гран (16,2 г) с измеренной начальной скоростью 905 м/с. Плотность воздуха ρ во время тестового выстрела составляла 1,2588 кг/м³ . Тестовой винтовке требовалась поправка на превышение 13,2 мил (45,38 МОА ) от нулевой дальности 300 м на широте 61 градус ( сила тяжести немного меняется с широтой), чтобы поразить цель размером с человеческий торс в мертвой точке на 1400 м. График баллистической кривой показал, что между 1392 м и 1408 м пули поразили бы цель высотой 60 см (2 фута). Это означает, что если бы была допущена ошибка в дальности всего в 0,6%, то цель высотой 60 см на расстоянии 1400 м была бы полностью пропущена. Когда та же цель была установлена на менее сложной дистанции 1000 м, ее можно было бы поразить на расстоянии от 987 м до 1013 м, то есть ошибка в дальности в 1,3% была бы приемлемой для поражения цели высотой 2 МОА снайперским патроном .338 Lapua Magnum. Это делает очевидным, что с увеличением расстояния, казалось бы, незначительные ошибки измерения и суждения становятся серьезной проблемой.
Ссылки
- ↑ Проектирование управления характеристиками полета снаряда, AMCP 706–242, Командование материально-технического обеспечения армии США, 1966 г.
- ↑ Армия (февраль 1965 г.), Внутренняя баллистика орудий (PDF) , Справочник по инженерному проектированию: Серия баллистики, Командование материально-технического обеспечения армии США, стр. 1–2, AMCP 706-150, архивировано из оригинала (PDF) 8 января 2016 г.
- ^ "Максимальная дальность стрельбы в упор и Battlesight Zero". 30 апреля 2010 г. Получено 24 декабря 2022 г.
- ^ "Улучшенный прицел Battlesight Zero для карабина M4 и винтовки M16A2" . Получено 11 сентября 2007 г.
- ^ "TM 9-1005-319-10 (2010) - Руководство оператора для винтовки, 5.56 MM, M16A2/M16A3/M4 (Battlesight Zero страницы 48-55)" (PDF) . Получено 2014-06-03 .
- ^ "Использование нуля на 400 метров с 5,45×39" . Получено 16 ноября 2014 г.
- ^ "Прогнозирование характеристик снаряда, устойчивости и свободного полета с использованием вычислительной гидродинамики, Вайнахт, Исследовательская лаборатория армии США, 2003" (PDF) . Архивировано из оригинала (PDF) 2021-01-21 . Получено 2022-06-02 .
- ^ "Баллистических коэффициентов не существует!" . Получено 12 января 2017 г.
- ^ "Weite Schüsse - drei (немецкий)" . Архивировано из оригинала 24 мая 2008 года . Проверено 24 декабря 2022 г.
- ^ "exterior ballistics". Архивировано из оригинала 8 августа 2003 года . Получено 12 января 2017 года .
- ^ "Пули класса LM, пули с очень высоким BC для стрельбы на большие дистанции в ветреную погоду". Архивировано из оригинала 19 февраля 2008 года . Получено 24 декабря 2022 года .
- ^ Литц, Брайан (8 марта 2021 г.) [Первоначально опубликовано 17 июня 2009 г., значительно расширено позже]. "Лучший баллистический коэффициент". Архивировано из оригинала 2 августа 2009 г.
- ^ ".338 Lapua Magnum product brochure from Lapua" (PDF) . Получено 24 декабря 2022 г. .[ постоянная мертвая ссылка ]
- ^ "300 grs Scenar HPBT brochure from Lapua" (PDF) . Получено 24 декабря 2022 .[ постоянная мертвая ссылка ]
- ^ "Ballistic Coefficients - Explained" (PDF) . Архивировано из оригинала (PDF) 29 октября 2013 года . Получено 12 января 2017 года .
- ^ "Математическое моделирование траекторий снарядов под влиянием эффектов окружающей среды, Райан Ф. Хук,∗Университет Нового Южного Уэльса в Канберре при Академии австралийских сил обороны, 2612, Австралия". Архивировано из оригинала 2018-02-04 . Получено 2018-02-02 .
- ^ "Форм-факторы: полезный инструмент анализа - блог Berger Bullets". 16 мая 2011 г. Получено 12 января 2017 г.
- ^ О Арте Пейсе Архивировано 29 августа 2008 г. на Wayback Machine
- ^ Pejsa, Arthur. "Pejsa Rifle Ballistics: программное обеспечение и книги Art Pejsa's Rifle ballistics". Pejsa Ballistics . Pejsa Ballistics. Архивировано из оригинала 8 февраля 2012 г. Получено 31 июля 2018 г.
- ^ Артур Дж. Пейса (2002). Справочник Пейсы по новой, точной баллистике . Kenwood Publishing. стр. 3.
- ^ ab Артур Дж. Пейса (2008). Новая точная баллистика стрелкового оружия . Kenwood Publishing. С. 65–76.
- ^ Артур Дж. Пейса (2008). Новая точная баллистика стрелкового оружия . Kenwood Publishing. стр. 63.
- ^ Артур Дж. Пейса (2002). Справочник Пейсы по новой, точной баллистике . Kenwood Publishing. стр. 34.
- ^ Артур Дж. Пейса (2002). Справочник Пейсы по новой, точной баллистике . Kenwood Publishing. стр. 4.
- ^ Артур Дж. Пейса (2008). Новая точная баллистика стрелкового оружия . Kenwood Publishing. С. 131–134.
- ^ Мейер, Роберт. «Пейса и обычные функции перетаскивания» . Проверено 12 января 2017 г.
- ^ Артур Дж. Пейса (2008). Новая точная баллистика стрелкового оружия . Kenwood Publishing. С. 33–35.
- ^ "Параметры испытаний и методы анализа: аэродинамические коэффициенты: что важно и как их измерить? Джефф Сиверт, системный инженер Arrow Tech Associates, Inc. 2012 NDIA Joint Armaments" (PDF) . Архивировано из оригинала (PDF) 2016-12-13 . Получено 2016-10-15 .
- ^ SPIN-73 Обновленная версия компьютерной программы Spinner, Уайт, 1973
- ^ Руководство по аэродинамическому проектированию тактического оружия, NSWC 1981
- ^ Улучшенное моделирование твердых тел для проектирования осесимметричных снарядов, 1988
- ^ "Цифровая имитационная модель с шестью степенями свободы для неуправляемых ракет со стабилизаторами" (PDF) . Архивировано из оригинала (PDF) 2017-02-21 . Получено 24 декабря 2022 .
- ^ "Lapua Ballistics App - Resources - Nammo Lapua". Архивировано из оригинала 20 декабря 2016 года . Получено 12 января 2017 года .
- ^ «НАБОР ИНСТРУМЕНТОВ ДЛЯ БАЛЛИСТИЧЕСКИХ ТАБЛИЦ НОВОГО ПОКОЛЕНИЯ НА ОСНОВЕ НАБК, Севсай Айтар Ортак, Умут Дурак, Умит Кутлуай, Корай Кучук, майор Кан Кандан, 23-й МЕЖДУНАРОДНЫЙ СИМПОЗИУМ ПО БАЛЛИСТИКЕ, ТАРРАГОНА, ИСПАНИЯ, 16-20 АПРЕЛЯ 2007 ГОДА» . Проверено 24 декабря 2022 г.
- ^ «Модель траектории BALCO 6/7-DoF, Пьер Вей, Дэниел Корриво, Томас А. Сайц, Вим де Рюйтер, Питер Стрёмбек, 29-й Международный симпозиум по баллистике, Эдинбург, Шотландия, 9–13 мая 2016 г.» . Проверено 24 декабря 2022 г.
- ^ Корриво, Д. (2017). «Валидация баллистического ядра вооружений НАТО для использования в системах управления огнем стрелкового оружия». Defence Technology . 13 (3): 188–199. doi : 10.1016/j.dt.2017.04.006 .
- ^ "Техническое обсуждение пуль ELD-X™ (Extremely Low Drag – eXpanding) и ELD™ Match (Extremely Low Drag Match) с наконечником Heat Shield™, Дэйв Эмари, октябрь 2015 г." (PDF) . Архивировано из оригинала (PDF) 2015-11-06 . Получено 2015-11-01 .
- ^ Чак Хоукс. «8x50R Lebel (8 мм Lebel)».
- ↑ Ричардсон против Соединенных Штатов, 72 Ct. Cl. 51 (1930)
- ^ MC DRAG — компьютерная программа для оценки коэффициентов сопротивления снарядов, Маккой, Лаборатория баллистических исследований армии США, 1981 г.
- ^ "Новая серия видео от Applied Ballistics « Daily Bulletin". Архивировано из оригинала 21 октября 2016 года . Получено 12 января 2017 года .
- ^ "Влияние геометрии боаттэйла на предельный цикл рыскания снарядов малого калибра, Брэдли Э. Хауэлл, Data Matrix Solutions, Абердинский испытательный полигон, MD 21005-5066 и Сидра И. Силтон и Пол Вайнахт, Исследовательский директорат по оружию и материалам, ARL, Абердинский испытательный полигон, MD 21005-5066, 27-я конференция AIAA по прикладной аэродинамике, 22–25 июня 2009 г., Сан-Антонио, Техас" (PDF) . Архивировано из оригинала (PDF) 2016-04-06 . Получено 2015-01-11 .
- ^ "ВЛИЯНИЕ НАРЕЗОК НАРЕЗКИ НА ХАРАКТЕРИСТИКИ БОЕПРИПАСОВ МАЛОГО КАЛИБРА Сидра И. Силтон и Пол Вайнахт Исследовательская лаборатория армии США Абердинский испытательный полигон, Мэриленд 21005-5066". Архивировано из оригинала 2015-01-11 . Получено 24 декабря 2022 .
- ^ "Национальные лаборатории Сандия: Пресс-релизы: Прототип самонаводящейся пули Сандия может поразить цель на расстоянии мили". Архивировано из оригинала 5 февраля 2012 года . Получено 12 января 2017 года .
- ^ "Управляемый снаряд калибра .50 — управляемая пуля DARPA" . Получено 27.09.2020 .
- ^ Кортни, Элия, Колин Моррис и Майкл Кортни. «Точные измерения коэффициентов сопротивления свободного полета с помощью любительского доплеровского радара». Библиотека Корнеллского университета (2016). arXiv :1608.06500
- ^ "Данные о коэффициенте сопротивления пуль Lapua для QuickTARGET Unlimited" (PDF) . Архивировано из оригинала (PDF) 2010-12-29 . Получено 24 декабря 2022 .
- ^ "Данные о компакт-дисках пуль Lapua (zip-файл)" . Получено 24 декабря 2022 г. .[ постоянная мертвая ссылка ]
- ^ "Использование доплеровского радара для генерации траекторных решений" (PDF) . Архивировано из оригинала (PDF) 2015-09-23 . Получено 2015-07-22 .
- ^ "Обзор баллистического калькулятора Hornady® 4DOF". Архивировано из оригинала 2016-08-23 . Получено 12 января 2017 .
- ^ "4DOF Ballistic Calculator" . Получено 12 января 2017 г. .
- ^ "Изменчивость сопротивления и использование "осевого форм-фактора" в калькуляторе траектории Hornady 4DOF™" (PDF) . Архивировано из оригинала (PDF) 19 октября 2016 г. . Получено 14 октября 2016 г. .
- ^ "Технический документ баллистического калькулятора Hornady® 4DOF™ (четыре степени свободы)" (PDF) . Архивировано из оригинала (PDF) 2016-10-19 . Получено 2016-10-14 .
- ^ "QuickTARGET Unlimited, Lapua Edition". Архивировано из оригинала 1 июля 2012 года . Получено 24 декабря 2022 года .
- ^ "Lapua Ballistics freeware external ballistic software for mobile phones". Архивировано из оригинала 1 июля 2012 года . Получено 24 декабря 2022 года .
- ^ "ВЛИЯНИЕ НАРЕЗОК НАРЕЗКИ НА ХАРАКТЕРИСТИКИ БОЕПРИПАСОВ МАЛОГО КАЛИБРА Сидра И. Силтон* и Пол Вайнахт Исследовательская лаборатория армии США Абердинский испытательный полигон, Мэриленд 21005-5066". Архивировано из оригинала 2012-10-06 . Получено 24 декабря 2022 .
- ^ ab Эффекты аэродинамического прыжка, вызванного равномерной последовательностью боковых импульсов - Джин Р. Купер, июль 2004 г.
- ^ «Понимание бросков вверх и вниз по склону при стрельбе на дальние дистанции: практическое руководство». backcountrymaven.com. 16 мая 2013 г. Архивировано из оригинала 25 ноября 2014 г. Получено 28 марта 2017 г.
- ^ Уильям Т. Макдональд (июнь 2003 г.). "INCLINED FIRE". Exterior Ballistics.com. Архивировано из оригинала 25 ноября 2014 г. Получено 12 января 2017 г.
- ^ Бекстранд, Том (6 февраля 2020 г.). «Влияние дождя на траекторию пули». Оружие и боеприпасы . Получено 24 декабря 2022 г.
- ^ Ненстиль Угол естественного откоса пули М80 (7,62 x 51 Nato), выпущенной под углом 32°
- ^ Неннстиль, Рупрехт. "длиннее" . Проверено 12 января 2017 г.
- ^ "Статьи - Applied Ballistics LLC". Архивировано из оригинала 7 января 2016 года . Получено 12 января 2017 года .
- ^ Ненстиэль Эффект Магнуса
- ^ Ненстиэль Сила Магнуса
- ^ Ненстиэль Момент Магнуса
- ^ "Гироскопический дрейф и ускорение Кореолиса" Брайана Литца. Архивировано из оригинала 2007-11-14 . Получено 2008-06-24 .
- ^ «Эффект Этвёша». www.cleonis.nl . Проверено 24 декабря 2022 г.
- ^ Лоури, Уильям (1997). Основы геофизики (иллюстрированное издание). Cambridge University Press. стр. 45. ISBN 0-521-46728-4.Выдержка из страницы 45
- ^ Исследовательская лаборатория армии США провела исследование в 1999 году по практическим ограничениям нескольких систем снайперского оружия и различных методов управления огнем. Анализ бюджета ошибок управления огнем снайперского оружия - Рэймонд фон Вальде, Деннис Метц, август 1999 г.
Внешние ссылки
Общая внешняя баллистика
- Tan, A.; Frick, CH & Castillo, O. (1987). «Траектория летящего мяча: пересмотр старого подхода». American Journal of Physics . 55 (1): 37. Bibcode :1987AmJPh..55...37T. doi :10.1119/1.14968.(Упрощенный расчет движения снаряда под действием силы сопротивления, пропорциональной квадрату скорости)
- "Идеальный баскетбольный бросок" (PDF) . (PDF) . Архивировано из оригинала (PDF) 5 марта 2006 г. . Получено 26 сентября 2005 г. .- баскетбольная баллистика.
Внешняя баллистика стрелкового оружия
- Программное обеспечение для расчета баллистики мяча
- Как летят пули? Рупрехт Неннстиль, Висбаден, Германия
- Статьи Exterior Ballistics.com Архивировано 06.03.2013 на Wayback Machine
- Краткий курс внешней баллистики
- Статьи о стрельбе на дальние дистанции Брайана Литца
- Анализ вероятностной зоны применения оружия (WEZ). Концептуальный обзор Брайана Литца. Архивировано 23 сентября 2015 г. на Wayback Machine.
- Weite Schüsse - часть 4, Базовое объяснение модели Пейсы Лутца Мёллера (на немецком языке)
- Программный движок баллистического математического обеспечения Patagonia Ballistics
- JBM Small Arms Ballistics с онлайн-калькуляторами баллистики
- Онлайн-калькулятор баллистической точки Bison Ballistics. Архивировано 15.05.2011 на Wayback Machine.
- Виртуальные эксперименты в аэродинамической трубе для определения аэродинамических характеристик боеприпасов малого калибра - Пол Вайнахт, Исследовательская лаборатория армии США, Абердинский испытательный полигон, штат Мэриленд
Внешняя баллистика артиллерии
- Управление огнем британской артиллерии - баллистика и данные
- Полевая артиллерия, том 6, Баллистика и боеприпасы
- Производство таблиц стрельбы для пушечной артиллерии, отчет BRL № 1371 Элизабет Р. Дикинсон, Лаборатории баллистических исследований Командования материально-технического обеспечения армии США, ноябрь 1967 г.
- NABK (баллистическое ядро НАТО) на основе баллистических таблиц следующего поколения, 23-й Международный симпозиум по баллистике, Таррагона, Испания, 16–20 апреля 2007 г.
- Калькулятор траектории на языке C++, который может вывести функцию перетаскивания из таблиц стрельбы
Бесплатное программное обеспечение для внешней баллистики стрелкового оружия
- Приложение Hawke X-ACT Pro БЕСПЛАТНОЕ для баллистики. iOS, Android, OSX и Windows.
- Бесплатная баллистика ChairGun Pro для винтовок с кольцевым воспламенением и пневматического оружия.
- Ballistic_XLR. (Электронная таблица MS Excel)] - существенное улучшение и модификация электронной таблицы Pejsa (ниже).
- GNU Exterior Ballistics Computer (GEBC) — открытый исходный код 3DOF баллистического компьютера для Windows, Linux и Mac — поддерживает модели сопротивления G1, G2, G5, G6, G7 и G8. Создано и поддерживается Дереком Йейтсом.
- Раздел баллистики 6mmbr.com содержит ссылки на 4 бесплатные внешние баллистические компьютерные программы.
- 2DOF и 3DOF RL McCoy - внешняя баллистика Gavre (zip-файл) - поддерживает модели сопротивления G1, G2, G5, G6, G7, G8, GS, GL, GI, GB и RA4
- PointBlank Ballistics (zip-файл) - модель сопротивления Siacci/Mayevski G1.
- Remington Shoot! Баллистический калькулятор для заводских боеприпасов Remington (на основе программного обеспечения Pinsoft Shoot!). - Модель сопротивления Siacci/Mayevski G1.
- Калькуляторы баллистики стрелкового оружия JBM Онлайн-калькуляторы траектории - Поддерживает модели сопротивления G1, G2, G5, G6, G7 (для некоторых снарядов экспериментально измеренные баллистические коэффициенты G7), G8, GI, GL и для некоторых снарядов, полученные с помощью доплеровского радара (C d ). [1]
- Баллистика Пейсы (таблица MS Excel) - модель Пейсы.
- Sharpshooter Friend (программное обеспечение Palm PDA) - модель Pejsa.
- Quick Target Unlimited, Lapua Edition — версия баллистического программного обеспечения QuickTARGET Unlimited (для загрузки требуется бесплатная регистрация) — поддерживает модели G1, G2, G5, G6, G7, G8, GL, GS Spherical 9/16"SAAMI, GS Spherical Don Miller, RA4, Soviet 1943, British 1909 Hatches Notebook и для некоторых снарядов Lapua модели сопротивления, полученные с помощью доплеровского радара (Cd).
- Программное обеспечение Lapua Ballistics Exterior для баллистики на Java или Android. Основано на моделях сопротивления, полученных с помощью доплеровского радара (Cd) для снарядов и патронов Lapua.
- Модель 6 DoF приложения Lapua Ballistics ограничена пулями Lapua для Android и iOS.
- BfX - Ballistics for Excel Набор функций надстроек MS Excel - Поддерживает модели сопротивления G1, G2, G5, G6, G7 G8 и RA4 и Pejsa, а также одну для пневматических винтовочных пуль. Возможность обработки пользовательских моделей, например, полученных с помощью доплеровского радара (Cd) для снарядов Lapua.
- GunSim «GunSim» — бесплатная браузерная программа-симулятор баллистики для Windows и Mac.
- BallisticSimulator «Ballistic Simulator» — бесплатная программа-симулятор баллистики для Windows.
- 5H0T Бесплатный онлайн-баллистический калькулятор с возможностью экспорта данных и построения графиков.
- SAKO Ballistics Архивировано 2016-03-15 в Wayback Machine Бесплатный онлайн-баллистический калькулятор от SAKO. Калькулятор также доступен в виде приложения для Android (возможно, и для iOS, я не знаю) под названием "SAKO Ballistics".
- py-ballisticcalc Библиотека Python LGPL для баллистических расчетов точечных масс.
- ^ "JBM Bullet Library". Архивировано из оригинала 3 мая 2010 года . Получено 24 декабря 2022 года .