Эфемерное поле
В электромагнетизме , затухающее поле или затухающая волна — это колеблющееся электрическое и/или магнитное поле, которое не распространяется как электромагнитная волна , но энергия которого пространственно сконцентрирована вблизи источника (колеблющиеся заряды и токи). Даже когда есть распространяющаяся электромагнитная волна, созданная (например, передающей антенной ), все равно можно идентифицировать как затухающее поле компонент электрического или магнитного поля, который не может быть приписан распространяющейся волне, наблюдаемой на расстоянии многих длин волн (например, дальнее поле передающей антенны).
Отличительной чертой исчезающего поля является отсутствие чистого потока энергии в этой области. Поскольку чистый поток электромагнитной энергии задается средним вектором Пойнтинга , это означает, что вектор Пойнтинга в этих областях, усредненный по полному циклу колебаний, равен нулю. [a]
Использование термина
Во многих случаях нельзя просто сказать, что поле является или не является «эванесцентным» – имея вектор Пойнтинга, средний к нулю в некотором направлении (или во всех направлениях). В большинстве случаев, где они существуют, эванесцентные поля просто рассматриваются и упоминаются так же, как и все другие электрические или магнитные поля, без какого-либо специального признания эванесцентности этих полей. Использование термина в основном ограничивается выделением части поля или решения в тех случаях, когда можно было бы ожидать только поля распространяющейся волны.
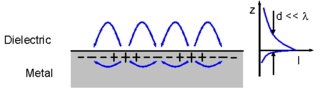
Например, на иллюстрации в верхней части статьи энергия действительно переносится в горизонтальном направлении. Однако в вертикальном направлении напряженность поля экспоненциально падает с увеличением расстояния над поверхностью. Это оставляет большую часть поля сосредоточенной в тонком пограничном слое очень близко к интерфейсу; по этой причине ее называют поверхностной волной . [1] Однако, несмотря на то, что энергия течет горизонтально, вдоль вертикали нет чистого распространения энергии от (или к) поверхности, так что можно было бы правильно описать поле как «затухающее в вертикальном направлении». Это один из примеров зависимости термина от контекста.
Повседневные электронные устройства и электроприборы окружены большими полями, которые являются мимолетными; их работа включает в себя переменные напряжения (создающие электрическое поле между ними) и переменные токи (создающие магнитное поле вокруг них), которые, как ожидается, будут переносить энергию только по внутренним проводам, но не наружу устройств. Несмотря на то, что термин «незаметный» не упоминается в этом обычном контексте, разработчики приборов все равно могут быть обеспокоены сохранением мимолетности, чтобы предотвратить или ограничить производство распространяющейся электромагнитной волны, которая может привести к потерям излучения , поскольку распространяющаяся волна «крадет» ее мощность у схемы или передает нежелательные помехи .
Термин «затухающее поле» действительно возникает в различных контекстах, где задействована распространяющаяся электромагнитная волна (даже если она ограничена). Затем этот термин различает компоненты электромагнитного поля, которые сопровождают распространяющуюся волну, но которые сами по себе не распространяются. В других, похожих случаях, где обычно ожидается распространяющаяся электромагнитная волна (например, свет, преломленный на границе раздела между стеклом и воздухом), этот термин используется для описания той части поля, где волна подавляется (например, свет, проходящий через стекло, падающий на границу раздела стекло-воздух, но за пределами критического угла ).
Хотя все электромагнитные поля классически управляются уравнениями Максвелла , различные технологии или проблемы имеют определенные типы ожидаемых решений, и когда первичные решения подразумевают распространение волн, термин «затухающий» часто применяется к компонентам поля или решениям, которые не обладают этим свойством.
Например, постоянная распространения полого металлического волновода является сильной функцией частоты ( дисперсионное соотношение ). Ниже определенной частоты ( частоты отсечки ) постоянная распространения становится мнимым числом. Решение волнового уравнения, имеющее мнимое волновое число, не распространяется как волна, а спадает экспоненциально, поэтому поле, возбужденное на этой более низкой частоте, считается затухающим. Можно также просто сказать, что распространение «запрещено» для этой частоты.
Формальное решение волнового уравнения может описывать моды, имеющие идентичную форму, но изменение постоянной распространения с действительной на мнимую, когда частота падает ниже частоты отсечки, полностью меняет физическую природу результата. Решение может быть описано как «режим отсечки» или «эванесцентный режим»; [2] [3] : 360 , в то время как другой автор просто скажет, что такого режима не существует. Поскольку эванесцентное поле, соответствующее моде, было вычислено как решение волнового уравнения, его часто обсуждают как «эванесцентную волну», даже если его свойства (такие как отсутствие переноса энергии) несовместимы с определением волны .
Хотя эта статья посвящена электромагнетизму, термин «эванесцентный» используется аналогичным образом в таких областях, как акустика и квантовая механика , где волновое уравнение возникает из вовлеченной физики. В этих случаях решения волнового уравнения, приводящие к мнимым постоянным распространения, также называются «эванесцентными» и обладают существенным свойством, заключающимся в том, что чистая энергия не передается, даже если есть ненулевое поле.
Применение затухающих волн
В оптике и акустике затухающие волны образуются, когда волны, распространяющиеся в среде, испытывают полное внутреннее отражение на ее границе, поскольку они падают на нее под углом, большим критического . [4] [5] Физическое объяснение существования затухающей волны состоит в том, что электрические и магнитные поля (или градиенты давления , в случае акустических волн) не могут быть разрывными на границе, как это было бы в случае отсутствия затухающего волнового поля. В квантовой механике физическое объяснение в точности аналогично — волновая функция Шредингера, представляющая движение частицы по нормали к границе, не может быть разрывной на границе.
Электромагнитные затухающие волны использовались для создания оптического давления излучения на малые частицы, чтобы захватить их для экспериментов или охладить до очень низких температур, а также для освещения очень малых объектов, таких как биологические клетки или отдельные молекулы белка и ДНК для микроскопии (как в флуоресцентном микроскопе полного внутреннего отражения ). Затухающая волна от оптического волокна может использоваться в газовом датчике, а затухающие волны фигурируют в технике инфракрасной спектроскопии, известной как ослабленное полное внутреннее отражение .
В электротехнике затухающие волны находятся в ближней зоне в пределах одной трети длины волны любой радиоантенны. Во время нормальной работы антенна излучает электромагнитные поля в окружающую ближнюю зону, и часть энергии поля поглощается, а остальная часть излучается в виде электромагнитных волн.
Недавно была изготовлена решетка Брэгга на основе графена (одномерный фотонный кристалл ), которая продемонстрировала свою пригодность для возбуждения поверхностных электромагнитных волн в периодической структуре с использованием метода призматической связи . [6]
В квантовой механике решения уравнения Шредингера в виде затухающих волн приводят к явлению волнового туннелирования .
В микроскопии системы, которые захватывают информацию, содержащуюся в затухающих волнах, могут использоваться для создания изображений со сверхвысоким разрешением . Материя излучает как распространяющиеся, так и затухающие электромагнитные волны. Обычные оптические системы захватывают только информацию в распространяющихся волнах и, следовательно, подвержены дифракционному пределу . Системы, которые захватывают информацию, содержащуюся в затухающих волнах, такие как суперлинза и сканирующая оптическая микроскопия ближнего поля , могут преодолеть дифракционный предел; однако эти системы затем ограничиваются способностью системы точно захватывать затухающие волны. [7] Ограничение на их разрешение задается выражением
где — максимальный волновой вектор , который можно разрешить, — расстояние между объектом и датчиком, — мера качества датчика .
В более общем смысле практические применения затухающих волн можно классифицировать как (1) те, в которых энергия, связанная с волной, используется для возбуждения какого-либо другого явления в области пространства, где исходная бегущая волна становится затухающей (например, как в флуоресцентном микроскопе полного внутреннего отражения ) или (2) те, в которых затухающая волна связывает две среды, в которых разрешены бегущие волны, и, следовательно, допускает передачу энергии или частицы между средами (в зависимости от используемого волнового уравнения), даже если в области пространства между двумя средами не разрешены решения для бегущей волны. Примером этого является волновое механическое туннелирование , и оно известно как затухающая волновая связь .
Полное внутреннее отражение света


Например, рассмотрим полное внутреннее отражение в двух измерениях с границей раздела между средами, лежащей на оси x, нормалью вдоль оси y и поляризацией вдоль оси z. Можно было бы ожидать, что для углов, приводящих к полному внутреннему отражению, решение будет состоять из падающей волны и отраженной волны, без прошедшей волны вообще, но такого решения, которое подчиняется уравнениям Максвелла, не существует . Уравнения Максвелла в диэлектрической среде налагают граничное условие непрерывности для компонент полей E || , H || , D y и B y . Для поляризации, рассматриваемой в этом примере, условия на E || и B y выполняются, если отраженная волна имеет ту же амплитуду, что и падающая, поскольку эти компоненты падающей и отраженной волн накладываются деструктивно. Однако их компоненты H x накладываются конструктивно, поэтому не может быть решения без неисчезающей прошедшей волны. Однако прошедшая волна не может быть синусоидальной, поскольку она тогда переносила бы энергию от границы, но поскольку падающая и отраженная волны имеют одинаковую энергию, это нарушило бы закон сохранения энергии . Поэтому мы приходим к выводу, что прошедшая волна должна быть неисчезающим решением уравнений Максвелла, которое не является бегущей волной, и единственными такими решениями в диэлектрике являются те, которые затухают экспоненциально: затухающие волны.
Математически, затухающие волны можно охарактеризовать волновым вектором , где один или несколько компонентов вектора имеют мнимое значение. Поскольку вектор имеет мнимые компоненты, он может иметь величину, которая меньше его действительных компонентов.
Если взять плоскость падения как плоскость при и границу раздела двух сред как плоскость при , то волновой вектор прошедшей волны имеет вид [8]
с и , где — величина волнового вектора прошедшей волны (то есть волновое число ), — угол преломления, а и — единичные векторы вдоль направления оси и направления оси соответственно.
Используя закон Снеллиуса , где , и — показатель преломления среды, в которой падает и отражается волна, показатель преломления среды, в которой проходит прошедшая волна, и угол падения соответственно,
- .
с .
Если часть условия полного внутреннего отражения как , выполняется, то
- .
Если поляризация перпендикулярна плоскости падения (вдоль направления), то электрическое поле любой из волн (падающей, отраженной или прошедшей) можно выразить как
где — единичный вектор в направлении оси.
Предполагая, что плоские волны равны , и подставляя переданный волновой вектор в , находим для переданной волны:
где — постоянная затухания , а — фазовая постоянная . игнорируется, поскольку не имеет физического смысла ( в данном случае — усиление волны вдоль направления y ).
Связь с затухающими волнами

В частности , в оптике связь затухающих волн относится к связи между двумя волнами из-за физического перекрытия того, что в противном случае было бы описано как затухающие поля, соответствующие распространяющимся волнам. [9]
Одним из классических примеров является нарушенное полное внутреннее отражение (FTIR) , в котором затухающее поле, очень близкое (см. график) к поверхности плотной среды, на которой волна обычно претерпевает полное внутреннее отражение, перекрывает другую плотную среду поблизости. Это нарушает полноту отражения, отводя часть мощности во вторую среду.
Связь между двумя оптическими волноводами может быть достигнута путем размещения волоконных сердечников близко друг к другу, так что затухающее поле, создаваемое одним элементом, возбуждает волну в другом волокне. Это используется для создания волоконно-оптических разветвителей и в ответвлении волокна . На радиочастотах (и даже оптических) такое устройство называется направленным ответвителем. Устройство обычно называют делителем мощности в случае микроволновой передачи и модуляции.
Связь затухающих волн является синонимом взаимодействия в ближнем поле в теории электромагнитного поля. В зависимости от природы исходного элемента, вовлеченное затухающее поле является либо преимущественно электрическим (емкостным), либо магнитным (индуктивным), в отличие от (распространяющихся) волн в дальнем поле, где эти компоненты связаны (идентичная фаза, в соотношении импеданса свободного пространства ). Связь затухающих волн происходит в неизлучающем поле вблизи каждой среды и, как таковая, всегда связана с материей; т. е. с индуцированными токами и зарядами внутри частично отражающей поверхности. В квантовой механике взаимодействие волновой функции может обсуждаться в терминах частиц и описываться как квантовое туннелирование .
Приложения
Связь затухающих волн обычно используется в фотонных и нанофотонных устройствах в качестве волноводных датчиков или соединителей (см., например, призматический соединитель ). [10]
Связь затухающих волн используется, например, для возбуждения диэлектрических микросферических резонаторов.
Эванесцентная связь, как взаимодействие в ближнем поле, является одной из проблем электромагнитной совместимости .
Соединение оптических волокон без потерь для ответвления волокна .
Связь затухающих волн играет важную роль в теоретическом объяснении необычайной оптической передачи . [11]
Связь с затухающими волнами используется для беспроводного питания устройств. [12] [13] [14]
Флуоресцентный микроскоп полного внутреннего отражения использует затухающую волну, создаваемую полным внутренним отражением, для возбуждения флуорофоров вблизи поверхности. Это полезно, когда необходимо изучить поверхностные свойства биологических образцов. [15]
Смотрите также
Примечания
- ^ Или, выражая поля E и H как фазоры , комплексный вектор Пойнтинга имеет нулевую действительную часть.
Ссылки
- ^ Такаяма, О.; Богданов, А.А.; Лавриненко, А.В. (2017). «Фотонные поверхностные волны на интерфейсах метаматериалов». Journal of Physics: Condensed Matter . 29 (46): 463001. Bibcode : 2017JPCM...29T3001T. doi : 10.1088/1361-648X/aa8bdd. PMID 29053474. S2CID 1528860.
- ^ IEEE Standard Dictionary of Electrical and Electronics Terms . Нью-Йорк, Нью-Йорк: Институт инженеров по электротехнике и электронике . 1992. С. 458. ISBN 978-1-55937-240-4. IEEE STD 100-1992.
- ^ Джексон, Джон Дэвид (1999). Классическая электродинамика (3-е изд.). John-Wiley. ISBN 047130932X.
- ^ Тинеке Тио (2006). «Яркое будущее для источников света субволновой длины». American Scientist . 94 (1): 40–47. doi :10.1511/2006.1.40.
- ^ Марстон, Филип Л.; Матула, Т. Дж. (май 2002 г.). «Рассеяние акустических затухающих волн». Журнал Акустического общества Америки . 111 (5): 2378. Bibcode : 2002ASAJ..111.2378M. doi : 10.1121/1.4778056.
- ^ Sreekanth, Kandammathe Valiyaveedu; Zeng, Shuwen; Shang, Jingzhi; Yong, Ken-Tye; Yu, Ting (2012). "Возбуждение поверхностных электромагнитных волн в решетке Брэгга на основе графена". Scientific Reports . 2 : 737. Bibcode :2012NatSR...2E.737S. doi :10.1038/srep00737. PMC 3471096 . PMID 23071901.
- ^ Нис, А., «Методы и ограничения субволновой визуализации», Успехи в визуализации и электронной физике, т. 163, июль 2010 г.
- ^ Хехт, Юджин (2017). Оптика (5-е глобальное издание). Пирсон. С. 135–137. ISBN 978-1-292-09693-3.
- ^ Zeng, Shuwen; Yu, Xia; Law, Wing-Cheung; Zhang, Yating; Hu, Rui; Dinh, Xuan-Quyen; Ho, Ho-Pui; Yong, Ken-Tye (2013). «Зависимость размера резонанса поверхностного плазмона, усиленного Au NP, на основе дифференциального фазового измерения». Датчики и приводы B: Химические . 176 : 1128–1133. Bibcode : 2013SeAcB.176.1128Z. doi : 10.1016/j.snb.2012.09.073.
- ^ Лова, Паола; Манфреди, Джованни; Коморетто, Давиде (2018). «Достижения в области обработки планарных 1D-фотонных кристаллов функциональным раствором». Advanced Optical Materials . 6 (24): 1800730. doi : 10.1002/adom.201800730 . hdl : 11567/928329 . ISSN 2195-1071.
- ^ Фань, Чжиюань; Чжань, Ли; Ху, Сяо; Ся, Юйсин (2008). «Критический процесс необычайной оптической передачи через периодический массив субволновых отверстий: связь затухающего поля с помощью отверстий». Optics Communications . 281 (21): 5467. Bibcode : 2008OptCo.281.5467F. doi : 10.1016/j.optcom.2008.07.077.
- ^ Karalis, Aristeidis; JD Joannopoulos; Marin Soljačić (февраль 2007 г.). "Эффективная беспроводная безызлучательная передача энергии на среднем расстоянии". Annals of Physics . 323 (1): 34. arXiv : physics/0611063 . Bibcode : 2008AnPhy.323...34K. doi : 10.1016/j.aop.2007.04.017. S2CID 1887505.
- ^ ««Эфемерная связь» может питать гаджеты без проводов», Селеста Бивер, NewScientist.com, 15 ноября 2006 г.
- ^ Беспроводная энергия может питать бытовую и промышленную электронику – пресс-релиз Массачусетского технологического института
- ^ Аксельрод, Д. (1 апреля 1981 г.). «Контакты клетка-субстрат, освещенные флуоресценцией полного внутреннего отражения». Журнал клеточной биологии . 89 (1): 141–145. doi :10.1083/jcb.89.1.141. PMC 2111781. PMID 7014571 .
Внешние ссылки
- Мимолетная волна s
- Анимация затухающих и распространяющихся волн на Youtube.com



































