Удлиненный додекаэдр
| Удлиненный додекаэдр | |
|---|---|
 | |
| Тип | Параллелоэдр |
| Лица | 8 ромбов 4 шестиугольника |
| Края | 28 |
| Вершины | 18 |
| Конфигурация вершины | (8) 4.6.6 (8) 4.4.6 (2) 4.4.4.4 |
| Группа симметрии | Двугранный (D 4h ), [4,2], (*422), порядок 16 |
| Группа вращения | D 4 , [4,2] + , (422), порядок 8 |
| Характеристики | Выпуклый |
| Сеть | |
 | |

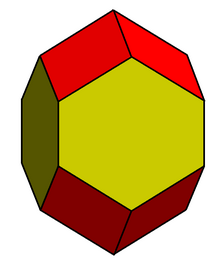
В геометрии удлиненный додекаэдр , [ 1] удлиненный ромбический додекаэдр , ромбогексагональный додекаэдр [2] или гексаромбический додекаэдр [3] — это выпуклый додекаэдр с 8 ромбическими и 4 шестиугольными гранями. Шестиугольники могут быть сделаны равносторонними или правильными в зависимости от формы ромбов. Его можно рассматривать как построенный из ромбического додекаэдра, удлиненного квадратной призмой .
Параллелоэдр
Наряду с ромбододекаэдром, это заполняющий пространство многогранник , один из пяти типов параллелоэдров, определенных Евграфом Федоровым, которые замостили пространство лицом к лицу с помощью трансляций. Он имеет 5 наборов параллельных ребер, называемых зонами или поясами.
Тесселяция
- Он может разбить все пространство на мозаику с помощью трансляций.
- Это ячейка Вигнера–Зейтца для некоторых объемно-центрированных тетрагональных решеток .
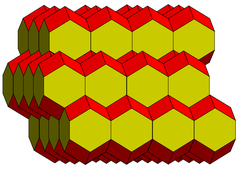 |
Это связано с ромбическими додекаэдрическими сотами с удлинением нулевым. Проецируемые перпендикулярно направлению удлинения, соты выглядят как квадратная мозаика с ромбами , спроецированными в квадраты .
Вариации
Расширенные додекаэдры можно деформировать в кубические объемы, используя соты как полусмещенную укладку кубов. Их также можно сделать вогнутыми, сместив 8 углов вниз на ту же величину, на которую смещаются центры.
 Копланарный многогранник |  Сеть |  Соты |
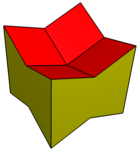 Вогнутый | 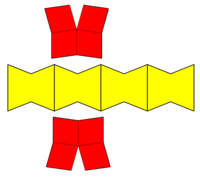 Сеть | 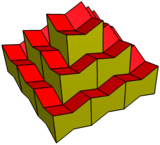 Соты |
Удлиненный додекаэдр может быть построен как сокращение однородного усеченного октаэдра , где квадратные грани сводятся к одиночным ребрам, а правильные шестиугольные грани сводятся к ромбическим граням с углом 60 градусов (или парам равносторонних треугольников). Эта конструкция чередует квадраты и ромбы на вершинах с 4 валентностями и имеет половину симметрии, симметрию D 2h , порядок 8.
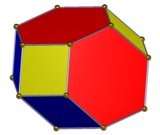 Сжатый усеченный октаэдр | 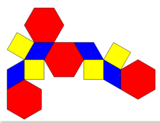 Сеть | 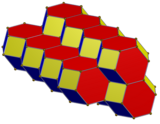 Соты |
Смотрите также
- Трапециевидно-ромбический додекаэдр
- Удлиненный октаэдр
- Удлиненный гиробифастигиум
Ссылки
- ^ Коксетер (1973) стр.257
- ^ Уильямсон (1979) стр. 169
- ^ Пять параллелоэдров Федорова в R³
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . Dover Publications, Inc. ISBN 0-486-23729-X. ромбо-гексагональный додекаэдр , стр. 169
- HSM Coxeter , Правильные многогранники , Третье издание, (1973), издание Dover, ISBN 0-486-61480-8 стр. 257
Внешние ссылки
- Вайсштейн, Эрик В. «Многогранник, заполняющий пространство». MathWorld .
- Вайсштейн, Эрик В. "Удлиненный додекаэдр". MathWorld .
- Равномерное заполнение пространства с использованием только ромбо-гексагональных додекаэдров
- Модель VRML удлиненного додекаэдра
