Кривая сопротивления

Кривая сопротивления или полярная кривая сопротивления — это соотношение между сопротивлением самолета и другими переменными, такими как подъемная сила, коэффициент подъемной силы, угол атаки или скорость. Она может быть описана уравнением или отображена в виде графика (иногда называемого «полярным графиком»). ^[1] Сопротивление может быть выражено как фактическое сопротивление или коэффициент сопротивления.

Кривые сопротивления тесно связаны с другими кривыми, которые не показывают сопротивление, такими как кривая требуемой мощности/скорости или кривая скорости снижения/скорости.

Значимые аэродинамические свойства крыльев самолета суммируются двумя безразмерными величинами , коэффициентами подъемной силы и сопротивления C _L и C _D . Как и другие подобные аэродинамические величины, они являются функциями только угла атаки α , числа Рейнольдса R _e и числа Маха M . C _L и C _D можно построить в зависимости от α или друг от друга. ^{[2] [3]}

Подъемная сила и сила сопротивления, L и D , масштабируются с одинаковым коэффициентом, чтобы получить CL и CD, поэтому L / D = CL / CD. L и D расположены _под прямым углом , причем D параллельна скорости _{свободного} потока ( относительной скорости окружающего удаленного воздуха _{) ,} поэтому результирующая сила R лежит под тем же углом к _​​D , что и линия от начала графика до соответствующей _точки CL , CD к оси _CD .

Если аэродинамическая поверхность удерживается под фиксированным углом атаки в аэродинамической трубе , и измеряются величина и направление результирующей силы, их можно построить с использованием полярных координат . Когда это измерение повторяется при разных углах атаки, получается кривая сопротивления. Данные о подъемной силе и сопротивлении были собраны таким образом в 1880-х годах Отто Лилиенталем и около 1910 года Густавом Эйфелем , хотя они не были представлены в терминах более поздних коэффициентов. Эйфель был первым, кто использовал название «полярное сопротивление», ^[4] однако кривые сопротивления редко строятся сегодня с использованием полярных координат.

В зависимости от типа самолета может потребоваться построить кривые сопротивления при разных числах Рейнольдса и Маха. Конструкция истребителя потребует кривых сопротивления при разных числах Маха, тогда как планеры, которые проводят свое время либо медленно летая в термических потоках, либо быстро между ними, могут потребовать кривых при разных числах Рейнольдса, но не подвержены эффектам сжимаемости. В ходе эволюции конструкции кривая сопротивления будет уточняться. Конкретный самолет может иметь разные кривые даже при одинаковых значениях R _e и M , в зависимости, например, от того, выпущены ли шасси и закрылки . ^[2]

Прилагаемая диаграмма показывает C _L против C _D для типичного легкого самолета . Минимальная точка C _D находится в крайней левой точке на графике. Одним из компонентов сопротивления является индуцированное сопротивление (неизбежный побочный эффект создания подъемной силы, который может быть уменьшен путем увеличения указанной скорости полета ). Оно пропорционально C _L ² . Другие механизмы сопротивления, паразитное и волновое сопротивление , имеют как постоянные компоненты, составляющие в сумме C _D0 , так и зависящие от подъемной силы вклады, которые увеличиваются пропорционально C _L ² . В общей сложности, тогда

CD = _CD0 + K. ₍ CL - _CL0 ) ² _.

Эффект C _L0 заключается в смещении кривой вверх по графику; физически это вызвано некоторой вертикальной асимметрией, такой как изогнутое крыло или конечный угол атаки , что обеспечивает минимальное сопротивление, создает подъемную силу и увеличивает максимальное аэродинамическое качество . ^{[2] [5]}

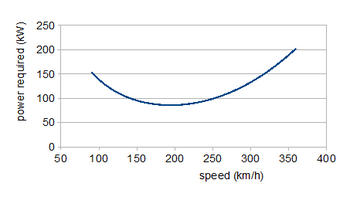
Одним из примеров использования кривой в процессе проектирования является расчет кривой требуемой мощности ( P _R ), которая отображает мощность, необходимую для устойчивого горизонтального полета в диапазоне рабочих скоростей. Вовлеченные силы получаются из коэффициентов путем умножения на (ρ/2).S V ² , где ρ — плотность атмосферы на высоте полета, S — площадь крыла, а V — скорость. В горизонтальном полете подъемная сила равна весу W , а тяга равна сопротивлению, поэтому

W = (ρ/2).S. V ² . C _L и

P _R = (ρ/2η).S. V ³ . C _D .

Дополнительный фактор V / η, где η — эффективность винта , во втором уравнении появляется, потому что P _R = (требуемая тяга) × V / η. Мощность, а не тяга, подходит для винтового самолета, так как она примерно не зависит от скорости; реактивные двигатели создают постоянную тягу. Поскольку вес постоянен, первое из этих уравнений определяет, как падает C _L с увеличением скорости. Подстановка этих значений C _L во второе уравнение с C _D из кривой сопротивления дает кривую мощности. Область низкой скорости показывает падение сопротивления, вызванного подъемной силой, через минимум, за которым следует увеличение сопротивления профиля на более высоких скоростях. Минимальная требуемая мощность на скорости 195 км/ч (121 миль/ч) составляет около 86 кВт (115 л. с.); для максимальной скорости 300 км/ч (186 миль/ч) требуется 135 кВт (181 л. с.). Полет на минимальной мощности обеспечит максимальную выносливость ; скорость для наибольшей дальности полета соответствует точке, где касательная к кривой мощности проходит через начало координат, около 240 км/ч (150 миль/ч). ^[6] )

Если доступно аналитическое выражение для кривой, полезные соотношения могут быть разработаны путем дифференцирования . Например, форма выше, слегка упрощенная путем подстановки C _L0 = 0, имеет максимум C _L / C _D при C _L ² = C _D0 /K . Для винтового самолета это максимальное условие выносливости и дает скорость 185 км/ч (115 миль/ч). Соответствующее максимальное условие дальности полета - это максимум C _L ^3/2 / C _D при C _L ² = 3.C _D0 /K , и поэтому оптимальная скорость составляет 244 км/ч (152 мили/ч). Эффекты приближения C _L0 = 0 составляют менее 5%; конечно, при конечном C _L0 = 0,1 аналитические и графические методы дают одинаковые результаты. ^[6]

Область полета с низкой скоростью известна как «задняя часть кривой мощности» или «за кривой мощности» ^{[7] [8]} (иногда «задняя часть кривой сопротивления»), где требуется больше тяги для поддержания полета на более низких скоростях. Это неэффективная область полета, поскольку уменьшение скорости требует увеличения тяги и, как следствие, увеличения расхода топлива. Она рассматривается как область полета «нестабильной скорости», поскольку в отличие от обычных обстоятельств, уменьшение скорости из-за увеличения угла атаки от ввода управления тангажем носа не исправится само собой, когда ввод управления прекратится. Вместо этого скорость останется низкой, а сопротивление будет постепенно накапливаться по мере того, как скорость продолжает уменьшаться, заставляя скорость снижения увеличиваться или скорость набора высоты уменьшаться, и это состояние будет сохраняться до тех пор, пока тяга не увеличится, угол атаки не уменьшится (что приведет к потере высоты) или сопротивление не уменьшится иным образом (например, путем уборки шасси ). Устойчивый полет за кривой мощности требует бдительного пилотирования, поскольку недостаточная тяга приведет к постоянному снижению скорости и соответствующему постоянному увеличению скорости снижения, что может остаться незамеченным и может быть трудно поддающимся корректировке на малой высоте. Нередким результатом является «болтание» самолета и его крушение недалеко от предполагаемого места посадки из-за того, что пилот не уменьшил угол атаки или не увеличил тягу вовремя, или из-за отсутствия достаточной тяги; последнее представляет особую опасность во время вынужденной посадки после отказа двигателя. ^{[8] [9]}

Неспособность контролировать скорость полета и скорость снижения при полете за кривой мощности стала причиной ряда известных авиационных происшествий, таких как рейс 214 авиакомпании Asiana Airlines . ^[9]

Для того чтобы самолет мог подняться под углом θ и на скорости V, его двигатель должен развивать большую мощность P сверх требуемой мощности P _R для уравновешивания сопротивления, испытываемого на этой скорости в горизонтальном полете и показанного на графике требуемой мощности. В горизонтальном полете P _R / V = ​​D, но при подъеме необходимо включить дополнительный компонент веса, то есть

P/V знак равно D + W .sin θ знак равно п _р / V + W .sin θ .

Следовательно, скорость набора высоты RC = V .sin θ = ( P - P _R )/ W . ^[10] Предположим, что установлен двигатель мощностью 135 кВт, необходимый для максимальной скорости 300 км/ч, тогда максимальная избыточная мощность составит 135 - 87 = 48 кВт при минимальной P _R и скорости набора высоты 2,4 м/с.

Для винтовых самолетов (включая турбовинтовые ) максимальная дальность полета и, следовательно, максимальная топливная эффективность достигаются при полете на скорости, обеспечивающей максимальное аэродинамическое качество. Это скорость, при которой можно преодолеть наибольшее расстояние при заданном количестве топлива. Максимальная выносливость (время в воздухе) достигается при более низкой скорости, когда аэродинамическое сопротивление минимально.

Для реактивных самолетов максимальная выносливость достигается при максимальном коэффициенте аэродинамического сопротивления. Максимальная дальность достигается при более высокой скорости. Это связано с тем, что реактивные двигатели создают тягу, а не мощность. Турбовинтовые самолеты создают некоторую тягу за счет выхлопных газов турбины, однако большая часть их мощности — это мощность, вырабатываемая пропеллером.

Скорость «дальнего крейсерского полета» (LRC) обычно выбирается так, чтобы обеспечить на 1% меньшую топливную эффективность, чем скорость максимальной дальности, поскольку это приводит к увеличению скорости на 3–5%. Однако топливо — не единственная предельная стоимость в работе авиакомпаний, поэтому скорость для наиболее экономичной эксплуатации (ECON) выбирается на основе индекса стоимости (CI), который представляет собой отношение стоимости времени к стоимости топлива. ^[11]

Без мощности планирующий самолет может двигаться только под действием силы тяжести. При угле скольжения θ вес имеет две составляющие: W .cos θ под прямым углом к ​​линии полета и W .sin θ, параллельную ей. Они уравновешиваются силами и подъемной силой соответственно, поэтому

W .cos θ = (ρ/2).S. В ² . CL и_​

В. ​sin θ = (ρ/2).S. В ² . С _Д.​

Разделив одно уравнение на другое, мы получаем, что угол скольжения определяется как tan θ = C _D / C _L . Наиболее интересными характеристиками летательных аппаратов при полете без двигателя являются скорость относительно земли, скажем, V _g , и скорость снижения V _s ; они отображаются путем построения графика V .sin θ = V _s против V .cos θ = V _g . Такие графики обычно называются полярными, и для их построения требуется угол скольжения как функция V. ^[12]

Один из способов нахождения решений двух уравнений силы — возвести их в квадрат, а затем сложить; это показывает, что возможные значения C _L , C _D лежат на окружности радиусом 2. W  /  S .ρ. V ² . Когда это наносится на поляру сопротивления, пересечение двух кривых определяет решение и его значение θ, считанное с помощью полярной оси. В качестве альтернативы, принимая во внимание, что скольжение обычно неглубокое, можно использовать приближение cos θ ≃ 1, хорошее для θ менее 10°, в уравнении подъемной силы и вычислить значение C _L для выбранного V , найдя C _L из поляры сопротивления и затем вычислив θ. ^[12]

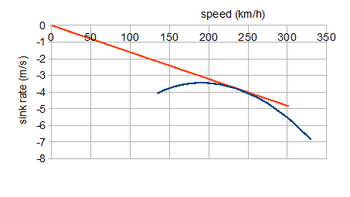
Пример поляры здесь показывает планирующие характеристики самолета, проанализированного выше, предполагая, что его полярность сопротивления не сильно изменяется неподвижным пропеллером. Прямая линия от начала координат до некоторой точки на кривой имеет градиент, равный углу скольжения на этой скорости, поэтому соответствующая касательная показывает наилучший угол скольжения tan ⁻¹ ( C _D / C _L ) _мин ≃ 3,3°. Это не самая низкая скорость снижения, но обеспечивает наибольшую дальность, требующую скорости 240 км/ч (149 миль/ч); минимальная скорость снижения около 3,5 м/с достигается при 180 км/ч (112 миль/ч), скоростях, показанных на предыдущих, силовых графиках. ^[12]

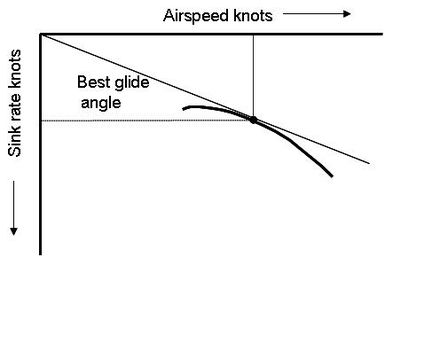
График, показывающий скорость снижения самолета (обычно планера ) в зависимости от его воздушной скорости , называется полярной кривой. ^[14] Полярные кривые используются для расчета минимальной скорости снижения планера, наилучшей подъемной силы над сопротивлением (L/D) и скорости полета . ^[13]

Полярная кривая планера выводится из теоретических расчетов или путем измерения скорости снижения при различных скоростях полета. Затем эти точки данных соединяются линией, чтобы сформировать кривую. Каждый тип планера имеет уникальную полярную кривую, и отдельные планеры несколько различаются в зависимости от гладкости крыла, сопротивления поверхности управления или наличия насекомых, грязи и дождя на крыле. Различные конфигурации планера будут иметь разные полярные кривые, например, одиночный или двойной полет, с водяным балластом и без него, разные настройки закрылков или с удлинениями законцовок крыла и без них. ^[14]

Знание лучшей скорости полета важно для использования характеристик планера. Двумя ключевыми показателями характеристик планера являются его минимальная скорость снижения и его лучшее качество планирования , также известное как лучший «угол планирования». Они происходят на разных скоростях. Знание этих скоростей важно для эффективного полета по пересеченной местности . В неподвижном воздухе полярная кривая показывает, что полет на минимальной скорости снижения позволяет пилоту оставаться в воздухе как можно дольше и набирать высоту как можно быстрее, но на этой скорости планер не пролетит так далеко, как если бы он летел со скоростью для лучшего планирования.

Лучшая скорость полета при встречном ветре определяется по графику путем смещения начала координат вправо по горизонтальной оси на скорость встречного ветра и проведения новой касательной линии. Эта новая воздушная скорость будет выше по мере увеличения встречного ветра, но приведет к наибольшему пройденному расстоянию. Общее правило заключается в том, чтобы добавить половину компонента встречного ветра к лучшему L/D для максимального расстояния. При попутном ветре начало координат смещается влево на скорость попутного ветра и проведения новой касательной линии. Скорость полета при попутном ветре будет находиться между минимальным снижением и лучшим L/D. ^[14]

В опускающемся воздухе полярная кривая смещается ниже в соответствии со скоростью снижения воздушной массы, и проводится новая касательная линия. Это покажет необходимость лететь быстрее в опускающемся воздухе, что дает опускающемуся воздуху меньше времени для снижения высоты планера. Соответственно, полярная кривая смещается вверх в соответствии со скоростью подъема, и проводится новая касательная линия. ^[13]

Увеличение веса не влияет на максимальную дальность полета планирующего самолета. Угол наклона определяется только отношением подъемной силы к лобовому сопротивлению. Увеличение веса потребует увеличения скорости полета для поддержания оптимального угла наклона, поэтому более тяжелый планирующий самолет будет иметь меньшую выносливость, поскольку он снижается по оптимальной траектории наклона с большей скоростью. ^[15]

Для гонок пилоты планеров часто используют водяной балласт, чтобы увеличить вес своего планера. Это увеличивает оптимальную скорость за счет низкой скорости и снижения скорости набора высоты в термических потоках. ^[16] Балласт также может использоваться для регулировки центра тяжести планера, что может улучшить его характеристики.

• Коэффициент лобового сопротивления
• Коэффициент подъемной силы
• Угол атаки
• Подъемная сила (сила)
• Теория подъемной линии

• Скорости полета планера — анимированное объяснение базовой полярной кривой с модификациями для нисходящего или восходящего воздуха, а также для встречного или попутного ветра.