Классификация разрывов

Непрерывные функции имеют первостепенное значение в математике , функциях и приложениях. Однако не все функции непрерывны. Если функция не является непрерывной в предельной точке (также называемой точкой накопления или точкой скопления ) своей области определения , говорят, что она имеет там разрыв . Множество всех точек разрыва функции может быть дискретным множеством , плотным множеством или даже всей областью определения функции.

Колебание функции в точке количественно определяет эти разрывы следующим образом :

• в устранимом разрыве расстояние, на которое отклоняется значение функции, является колебанием;
• в скачкообразном разрыве величина скачка является колебанием (предполагая, что значение в точке лежит между этими пределами двух сторон);
• В существенном разрыве колебание измеряет отсутствие предела .

Особый случай — если функция расходится к бесконечности или минус бесконечности , в этом случае колебание не определено (в расширенных действительных числах это устранимый разрыв).

Для каждого из следующих случаев рассмотрим действительную функцию действительной переменной, определенную в окрестности точки , в которой она разрывна.${\displaystyle f}$${\displaystyle x,}$${\displaystyle x_{0}}$${\displaystyle f}$

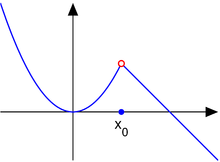
Рассмотрим кусочную функцию $${\displaystyle f(x)={\begin{cases}x^{2}&{\text{ for }}x<1\\0{\text{ (или, возможно, не определено)}}&{\text{ for }}x=1\\2-x&{\text{ for }}x>1\end{cases}}}$$

Дело в устранимом разрыве . Для такого рода разрыва:${\displaystyle x_{0}=1}$

Односторонний предел с отрицательного направления: и односторонний предел с положительного направления: при оба существуют, конечны и равны Другими словами, поскольку два односторонних предела существуют и равны, предел при приближении существует и равен этому же значению. Если фактическое значение не равно или не определено, то называется$${\displaystyle L^{-}=\lim _{x\to x_{0}^{-}}f(x)}$$$${\displaystyle L^{+}=\lim _{x\to x_{0}^{+}}f(x)}$$${\displaystyle x_{0}}$ ${\displaystyle L=L^{-}=L^{+}.}$${\displaystyle L}$${\displaystyle f(x)}$${\displaystyle x}$${\displaystyle x_{0}}$${\displaystyle f\left(x_{0}\right)}$${\displaystyle L,}$${\displaystyle x_{0}}$устранимый разрыв . Этот разрыв можно устранить, чтобы сделатьфункцию непрерывной приили, точнее, функция непрерывна при${\displaystyle f}$${\displaystyle x_{0},}$$${\displaystyle g(x)={\begin{cases}f(x)&x\neq x_{0}\\L&x=x_{0}\end{cases}}}$$${\displaystyle x=x_{0}.}$

Термин «устранимый разрыв» иногда расширяют, включая в него устранимую особенность , в которой пределы в обоих направлениях существуют и равны, в то время как функция не определена в точке ^[a]. Такое использование является злоупотреблением терминологией , поскольку непрерывность и разрывность функции — это понятия, определенные только для точек в области определения функции.${\displaystyle x_{0}.}$

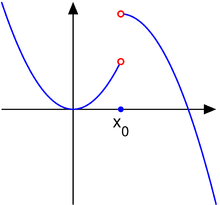
Рассмотрим функцию$${\displaystyle f(x)={\begin{cases}x^{2}&{\mbox{ for }}x<1\\0{\text{ (или, возможно, не определено)}}&{\mbox{ for }}x=1\\2-(x-1)^{2}&{\mbox{ for }}x>1\end{cases}}}$$

Тогда, дело в том,${\displaystyle x_{0}=1}$скачок непрерывности .

В этом случае, единственный предел не существует, поскольку односторонние пределы и существуют и конечны, но не равны: поскольку, предел не существует. Тогда, называется скачкообразным разрывом , ступенчатым разрывом или разрывом первого рода . Для этого типа разрыва функция может иметь любое значение при${\displaystyle L^{-}}$${\displaystyle L^{+}}$${\displaystyle L^{-}\neq L^{+},}$${\displaystyle L}$${\displaystyle x_{0}}$${\displaystyle f}$${\displaystyle x_{0}.}$

Для существенного разрыва по крайней мере один из двух односторонних пределов не существует в . (Обратите внимание, что один или оба односторонних предела могут быть ).${\displaystyle \mathbb {R} }$${\displaystyle \pm \infty }$

Рассмотрим функцию$${\displaystyle f(x)={\begin{cases}\sin {\frac {5}{x-1}}&{\text{ for }}x<1\\0&{\text{ for }}x=1\\{\frac {1}{x-1}}&{\text{ for }}x>1.\end{cases}}}$$

Тогда, дело в том,${\displaystyle x_{0}=1}$существенный разрыв .

В этом примере и не существуют в , таким образом удовлетворяя условию существенной разрывности. Так же как и существенный разрыв, бесконечный разрыв или разрыв второго рода. (Это отличается от существенной сингулярности , которая часто используется при изучении функций комплексных переменных ).${\displaystyle L^{-}}$${\displaystyle L^{+}}$${\displaystyle \mathbb {R} }$${\displaystyle x_{0}}$

Предположим, что — функция определена на интервале, мы обозначим через множество всех разрывов на Под мы будем подразумевать множество всех таких, которые имеют устранимый разрыв в Аналогично через мы обозначим множество, образованное всеми такими, которые имеют скачок разрыва в Множество всех таких, которые имеют существенный разрыв в будет обозначаться через Конечно, тогда${\displaystyle f}$${\displaystyle I\subseteq \mathbb {R} ,}$${\displaystyle D}$${\displaystyle f}$${\displaystyle Я.}$${\displaystyle R}$${\displaystyle x_{0}\in I}$${\displaystyle f}$${\displaystyle x_{0}.}$${\displaystyle J}$${\displaystyle x_{0}\in I}$${\displaystyle f}$${\displaystyle x_{0}.}$${\displaystyle x_{0}\in I}$${\displaystyle f}$${\displaystyle x_{0}}$${\displaystyle Э.}$${\displaystyle D=R\чашка J\чашка E.}$

В литературе актуальны два следующих свойства множества .${\displaystyle D}$

• Множество является множеством . Множество точек, в которых функция непрерывна, всегда является множеством ( см. ^[2] ).${\displaystyle D}$${\displaystyle F_{\сигма}}$${\displaystyle G_{\delta}}$
• Если на интервале монотонно, то не более чем счетно и Это теорема Фроды .${\displaystyle Я,}$ ${\displaystyle f}$${\displaystyle D}$${\displaystyle D=J.}$

Том Апостол ^[3] частично следует классификации выше, рассматривая только устранимые и скачкообразные разрывы. Его цель — изучить разрывы монотонных функций, в основном, чтобы доказать теорему Фроды. С той же целью Вальтер Рудин ^[4] и Карл Р. Стромберг ^[5] также изучают устранимые и скачкообразные разрывы, используя разные терминологии. Однако, далее, оба автора утверждают, что всегда является счетным множеством (см. ^{[6] [7]} ).${\displaystyle R\чашка J}$

Термин «существенная прерывность» использовался в математическом контексте уже в 1889 году. ^[8] Однако самое раннее использование термина вместе с математическим определением, по-видимому, было дано в работе Джона Клипперта. ^[9] В ней Клипперт также классифицировал сами существенные прерывности, разделив множество на три следующих множества:${\displaystyle E}$

$${\displaystyle E_{1}=\left\{x_{0}\in I:\lim _{x\to x_{0}^{-}}f(x){\text{ и }}\lim _{x\to x_{0}^{+}}f(x){\text{ не существуют в }}\mathbb {R} \right\},}$$$${\displaystyle E_{2}=\left\{x_{0}\in I:\ \lim _{x\to x_{0}^{-}}f(x){\text{ exists in }}\mathbb {R} {\text{ and }}\lim _{x\to x_{0}^{+}}f(x){\text{ does not exist in }}\mathbb {R} \right\},}$$$${\displaystyle E_{3}=\left\{x_{0}\in I:\ \lim _{x\to x_{0}^{-}}f(x){\text{ does not exist in }}\mathbb {R} {\text{ and }}\lim _{x\to x_{0}^{+}}f(x){\text{ exists in }}\mathbb {R} \right\}.}$$

Конечно, Whenever называется существенной разрывностью первого рода . Any называется существенной разрывностью второго рода. Поэтому он расширяет множество, не теряя его характеристики счетности, утверждая следующее:${\displaystyle E=E_{1}\cup E_{2}\cup E_{3}.}$${\displaystyle x_{0}\in E_{1},}$ ${\displaystyle x_{0}}$${\displaystyle x_{0}\in E_{2}\cup E_{3}}$${\displaystyle R\cup J}$

• Множество счетно.${\displaystyle R\cup J\cup E_{2}\cup E_{3}}$

Когда и является ограниченной функцией, хорошо известно о важности множества в отношении интегрируемости по Риману . Фактически, теорема Лебега (также называемая теоремой Лебега-Витали) утверждает, что интегрируемо по Риману на тогда и только тогда, когда является множеством с нулевой мерой Лебега.${\displaystyle I=[a,b]}$${\displaystyle f}$${\displaystyle D}$${\displaystyle f.}$${\displaystyle f}$${\displaystyle I=[a,b]}$${\displaystyle D}$

В этой теореме, кажется, что все типы разрывов имеют одинаковый вес на препятствии, что ограниченная функция может быть интегрируемой по Риману на Поскольку счетные множества являются множествами меры Лебега нуль, а счетное объединение множеств с мерой Лебега нуль все еще является множеством меры Лебега нуль, мы видим теперь, что это не так. Фактически, разрывы в множестве абсолютно нейтральны в отношении интегрируемости по Риману Главными разрывами для этой цели являются существенные разрывы первого рода, и, следовательно, теорема Лебега-Витали может быть переписана следующим образом:${\displaystyle f}$${\displaystyle [a,b].}$${\displaystyle R\cup J\cup E_{2}\cup E_{3}}$${\displaystyle f.}$

• Ограниченная функция интегрируема по Риману на тогда и только тогда, когда соответствующее множество всех существенных разрывов первого рода имеет нулевую меру Лебега.${\displaystyle f,}$${\displaystyle [a,b]}$${\displaystyle E_{1}}$${\displaystyle f}$

Случай, когда соответствуют следующим известным классическим дополнительным ситуациям интегрируемости по Риману ограниченной функции :${\displaystyle E_{1}=\varnothing }$${\displaystyle f:[a,b]\to \mathbb {R} }$

• Если имеет правосторонний предел в каждой точке , то интегрируемо по Риману (см. ^[10] )${\displaystyle f}$${\displaystyle [a,b[}$${\displaystyle f}$${\displaystyle [a,b]}$
• Если имеет левосторонний предел в каждой точке, то интегрируемо ли по Риману${\displaystyle f}$${\displaystyle ]a,b]}$${\displaystyle f}$${\displaystyle [a,b].}$
• Если является регулируемой функцией на , то интегрируема ли функция Римана на${\displaystyle f}$${\displaystyle [a,b]}$${\displaystyle f}$${\displaystyle [a,b].}$

Функция Томаэ разрывна в каждой ненулевой рациональной точке , но непрерывна в каждой иррациональной точке. Легко видеть, что все эти разрывы устранимы. Согласно первому абзацу, не существует функции, которая непрерывна в каждой рациональной точке, но разрывна в каждой иррациональной точке.

Индикаторная функция рациональных чисел, также известная как функция Дирихле , всюду разрывна . Эти разрывы все существенны и первого рода.

Рассмотрим теперь троичное множество Кантора и его индикаторную (или характеристическую) функцию. Один из способов построения множества Кантора дается формулой , где множества получаются путем рекуррентного сопоставления согласно ${\displaystyle {\mathcal {C}}\subset [0,1]}$$${\displaystyle \mathbf {1} _{\mathcal {C}}(x)={\begin{cases}1&x\in {\mathcal {C}}\\0&x\in [0,1]\setminus {\mathcal {C}}.\end{cases}}}$$ ${\displaystyle {\mathcal {C}}}$${\textstyle {\mathcal {C}}:=\bigcap _{n=0}^{\infty }C_{n}}$${\displaystyle C_{n}}$$${\displaystyle C_{n}={\frac {C_{n-1}}{3}}\cup \left({\frac {2}{3}}+{\frac {C_{n-1}}{3}}\right){\text{ for }}n\geq 1,{\text{ and }}C_{0}=[0,1].}$$

Ввиду разрывов функции предположим точку${\displaystyle \mathbf {1} _{\mathcal {C}}(x),}$${\displaystyle x_{0}\not \in {\mathcal {C}}.}$

Следовательно, существует множество, используемое в формулировке , которое не содержит То есть принадлежит одному из открытых интервалов, которые были удалены при построении Таким образом, имеет окрестность без точек (Другим способом тот же вывод следует с учетом того, что является замкнутым множеством, а значит, его дополнительное по отношению к является открытым). Следовательно, принимает значение ноль только в некоторой окрестности Следовательно , непрерывно в${\displaystyle C_{n},}$${\displaystyle {\mathcal {C}}}$${\displaystyle x_{0}.}$${\displaystyle x_{0}}$${\displaystyle C_{n}.}$${\displaystyle x_{0}}$${\displaystyle {\mathcal {C}}.}$${\displaystyle {\mathcal {C}}}$${\displaystyle [0,1]}$${\displaystyle \mathbf {1} _{\mathcal {C}}}$${\displaystyle x_{0}.}$${\displaystyle \mathbf {1} _{\mathcal {C}}}$${\displaystyle x_{0}.}$

Это означает, что множество всех разрывов на интервале является подмножеством Поскольку является несчетным множеством с нулевой мерой Лебега , то является также множеством с нулевой мерой Лебега и, следовательно, в соответствии с теоремой Лебега-Витали является интегрируемой по Риману функцией.${\displaystyle D}$${\displaystyle \mathbf {1} _{\mathcal {C}}}$${\displaystyle [0,1]}$${\displaystyle {\mathcal {C}}.}$${\displaystyle {\mathcal {C}}}$${\displaystyle D}$ ${\displaystyle \mathbf {1} _{\mathcal {C}}}$

Точнее говоря , фактически, поскольку является нигде не плотным множеством, если то никакая окрестность не может содержаться в Таким образом, любая окрестность содержит точки и точки, которые не являются В терминах функции это означает, что и и не существуют. То есть, где через, как и прежде, мы обозначаем множество всех существенных разрывов первого рода функции Очевидно,${\displaystyle D={\mathcal {C}}.}$${\displaystyle {\mathcal {C}}}$${\displaystyle x_{0}\in {\mathcal {C}}}$ ${\displaystyle \left(x_{0}-\varepsilon ,x_{0}+\varepsilon \right)}$${\displaystyle x_{0},}$${\displaystyle {\mathcal {C}}.}$${\displaystyle x_{0}\in {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}.}$${\displaystyle \mathbf {1} _{\mathcal {C}}}$${\textstyle \lim _{x\to x_{0}^{-}}\mathbf {1} _{\mathcal {C}}(x)}$${\textstyle \lim _{x\to x_{0}^{+}}1_{\mathcal {C}}(x)}$${\displaystyle D=E_{1},}$${\displaystyle E_{1},}$${\displaystyle \mathbf {1} _{\mathcal {C}}.}$${\textstyle \int _{0}^{1}\mathbf {1} _{\mathcal {C}}(x)dx=0.}$

Пусть открытый интервал, пусть будет дифференцируем на и пусть будет производной от То есть, для каждого . Согласно теореме Дарбу , производная функция удовлетворяет свойству промежуточного значения. Функция , конечно, может быть непрерывной на интервале, в этом случае теорема Больцано также применима. Напомним, что теорема Больцано утверждает, что каждая непрерывная функция удовлетворяет свойству промежуточного значения. С другой стороны, обратное неверно: теорема Дарбу не предполагает, что она непрерывна, а свойство промежуточного значения не подразумевает, что она непрерывна на${\displaystyle I\subseteq \mathbb {R} }$${\displaystyle F:I\to \mathbb {R} }$${\displaystyle I,}$${\displaystyle f:I\to \mathbb {R} }$${\displaystyle F.}$${\displaystyle F'(x)=f(x)}$${\displaystyle x\in I}$${\displaystyle f:I\to \mathbb {R} }$${\displaystyle f}$${\displaystyle I,}$${\displaystyle f}$${\displaystyle f}$${\displaystyle I.}$

Теорема Дарбу, однако, имеет непосредственное следствие относительно типа разрывов, которые могут иметь. Фактически, если является точкой разрыва , то обязательно является существенным разрывом . ^[11] Это означает, в частности, что следующие две ситуации не могут возникнуть:${\displaystyle f}$${\displaystyle x_{0}\in I}$${\displaystyle f}$${\displaystyle x_{0}}$${\displaystyle f}$

Кроме того, необходимо исключить еще две ситуации (см. Джон Клипперт ^[12] ):

Заметим, что всякий раз, когда одно из условий (i), (ii), (iii) или (iv) выполняется для некоторого числа, можно сделать вывод, что не обладает первообразной, , на интервале .${\displaystyle x_{0}\in I}$${\displaystyle f}$${\displaystyle F}$${\displaystyle I}$

С другой стороны, можно ввести новый тип разрыва относительно любой функции : существенный разрыв функции называется фундаментальным существенным разрывом , если${\displaystyle f:I\to \mathbb {R} }$${\displaystyle x_{0}\in I}$${\displaystyle f}$${\displaystyle f}$

$${\displaystyle \lim _{x\to x_{0}^{-}}f(x)\neq \pm \infty }$$и$${\displaystyle \lim _{x\to x_{0}^{+}}f(x)\neq \pm \infty .}$$

Поэтому, если есть разрыв производной функции , то обязательно есть фундаментальный существенный разрыв функции .${\displaystyle x_{0}\in I}$${\displaystyle f:I\to \mathbb {R} }$${\displaystyle x_{0}}$${\displaystyle f}$

Заметим также, что когда и является ограниченной функцией, как в предположениях теоремы Лебега, мы имеем для всех : и Поэтому любой существенный разрыв является фундаментальным.${\displaystyle I=[a,b]}$${\displaystyle f:I\to \mathbb {R} }$${\displaystyle x_{0}\in (a,b)}$$${\displaystyle \lim _{x\to x_{0}^{\pm }}f(x)\neq \pm \infty ,}$$$${\displaystyle \lim _{x\to a^{+}}f(x)\neq \pm \infty ,}$$$${\displaystyle \lim _{x\to b^{-}}f(x)\neq \pm \infty .}$$${\displaystyle f}$

• Устранимая особенность  – неопределенная точка на голоморфной функции, которую можно сделать регулярной
• Математическая сингулярность  – точка, в которой функция, кривая или другой математический объект ведет себя нерегулярно.Pages displaying short descriptions of redirect targets
• Расширение по непрерывности  – топологическое пространство, в котором точка и замкнутое множество, если они не пересекаются, разделимы окрестностями.Pages displaying wikidata descriptions as a fallback
• Гладкость  – число производных функции (математика)
  • Геометрическая непрерывность  – Число производных функции (математика)Pages displaying short descriptions of redirect targets
  • Параметрическая непрерывность  – число производных функции (математика)Pages displaying short descriptions of redirect targets

• Малик, СК; Арора, Савита (1992). Математический анализ (2-е изд.). Нью-Йорк: Wiley. ISBN 0-470-21858-4.

• «Прерывистый». PlanetMath .
• «Разрыв» Эда Пегга-младшего , The Wolfram Demonstrations Project , 2007.
• Вайсштейн, Эрик В. «Разрыв». MathWorld .
• Кудрявцев, Л. Д. (2001) [1994]. "Точка разрыва". Энциклопедия математики . Издательство EMS .