Дельта-v
Delta- v (также известное как « изменение скорости »), обозначаемое и произносимое как deltah-vee , используемое в динамике полета космического корабля , является мерой импульса на единицу массы космического корабля, необходимого для выполнения маневра, такого как запуск с планеты или луны или посадка на них, или орбитальный маневр в космосе . Это скаляр , имеющий единицы скорости . В данном контексте это не то же самое, что физическое изменение скорости указанного космического корабля.
Простым примером может служить случай обычного ракетного космического корабля, который достигает тяги за счет сжигания топлива. Таким образом, delta- v такого космического корабля будет изменением скорости, которого космический корабль может достичь, сжигая весь свой топливный груз.
Delta- v вырабатывается реактивными двигателями , такими как ракетные двигатели , и пропорциональна тяге на единицу массы и времени сгорания. Она используется для определения массы топлива, необходимого для данного маневра, через уравнение Циолковского для ракеты .
Для множественных маневров дельта- v суммируется линейно.
Для межпланетных миссий дельта- v часто наносится на график , который отображает требуемую миссию дельта- v как функцию даты запуска.
Определение
где
Изменение скорости полезно во многих случаях, например, для определения изменения импульса ( импульса ), где: , где — импульс, а m — масса.
Конкретные случаи
При отсутствии внешних сил: где - ускорение координаты.
Когда тяга прикладывается в постоянном направлении ( в/| в | постоянна) это упрощается до: что является просто величиной изменения скорости . Однако это соотношение не выполняется в общем случае: если, например, постоянное однонаправленное ускорение меняет знак после ( t 1 − t 0 )/2 , то разность скоростей равна 0, но delta- v такая же, как и для нереверсированной тяги.
Для ракет «отсутствие внешних сил» означает отсутствие гравитации и атмосферного сопротивления, а также отсутствие аэростатического противодавления на сопле, и, следовательно, вакуум I sp используется для расчета дельта- v мощности транспортного средства через уравнение ракеты . Кроме того, затраты на атмосферные потери и гравитационное сопротивление добавляются в бюджет дельта- v при запуске с поверхности планеты. [1]
Орбитальные маневры
Маневры на орбите производятся путем включения двигателя , чтобы создать силу реакции, действующую на космический корабль. Величина этой силы будет
| ( 1 ) |
где
- v exh — скорость выхлопных газов в корпусе ракеты
- ρ — расход топлива в камеру сгорания
Ускорение космического корабля, вызванное этой силой, будет равно
| ( 2 ) |
где m — масса космического корабля
Во время сгорания масса космического корабля будет уменьшаться из-за использования топлива, производная массы по времени составит
| ( 3 ) |
Если теперь направление силы, т.е. направление сопла , зафиксировано во время горения, то можно получить увеличение скорости от силы движителя горения, начинающееся в момент времени и заканчивающееся в момент времени t 1 , как
| ( 4 ) |
Изменяя переменную интегрирования от времени t к массе космического корабля m, получаем
| ( 5 ) |
Предполагая, что это постоянная величина, не зависящая от количества оставшегося топлива, это соотношение интегрируется в
| ( 6 ) |
что является уравнением ракеты Циолковского .
Если, например, 20% стартовой массы составляет топливо, дающее постоянную 2100 м/с (типичное значение для гидразинового двигателя), то мощность системы управления реакцией составит
Если — непостоянная функция количества оставшегося топлива [2], то мощность системы управления реакцией вычисляется с помощью интеграла ( 5 ).
Ускорение ( 2 ), вызванное силой двигателя, является просто дополнительным ускорением, которое следует добавить к другим ускорениям (сила на единицу массы), действующим на космический корабль, и орбита может быть легко распространена с помощью численного алгоритма, включающего также эту силу двигателя. [3] Но для многих целей, как правило, для исследований или для оптимизации маневра, они аппроксимируются импульсными маневрами, как показано на рисунке 1 с , как указано в ( 4 ). Например, можно использовать подход «заплатанных конических сечений», моделирующий маневр как переход с одной орбиты Кеплера на другую путем мгновенного изменения вектора скорости.

Это приближение с импульсными маневрами в большинстве случаев очень точно, по крайней мере, когда используется химическое движение. Для систем с низкой тягой, как правило, электрических двигательных систем, это приближение менее точно. Но даже для геостационарных космических аппаратов, использующих электрические двигатели для управления вне плоскости с периодами работы двигателей, растянутыми на несколько часов вокруг узлов, это приближение справедливо.
Производство
Delta- v обычно обеспечивается тягой ракетного двигателя , но может быть создана и другими двигателями. Скорость изменения delta- v во времени — это величина ускорения, вызванного двигателями , т. е. тяга на общую массу транспортного средства. Фактический вектор ускорения можно найти, добавив тягу на массу к вектору силы тяжести и векторам, представляющим любые другие силы, действующие на объект.
Необходимая общая дельта- v является хорошей отправной точкой для принятия ранних проектных решений, поскольку рассмотрение дополнительных сложностей откладывается на более поздние этапы процесса проектирования.
Уравнение ракеты показывает, что необходимое количество топлива резко возрастает с ростом delta- v . Поэтому в современных двигательных системах космических аппаратов значительные исследования направлены на снижение общей delta- v, необходимой для данного космического полета, а также на проектирование космических аппаратов, способных производить большую delta- v .
Увеличение дельта- v, обеспечиваемое двигательной системой, может быть достигнуто за счет:
- постановка
- увеличение удельного импульса
- улучшение массовой доли топлива
Множественные маневры
Поскольку массовые соотношения применяются к любому конкретному сжиганию, при последовательном выполнении нескольких маневров массовые соотношения умножаются.
Таким образом, можно показать, что при условии, что скорость истечения фиксирована, это означает, что дельта- v можно суммировать:
Когда m 1 , m 2 — это массовые отношения маневров, а v 1 , v 2 — это дельта -v первого и второго маневров , где V = v 1 + v 2 и M = m 1 m 2 . Это просто уравнение ракеты, примененное к сумме двух маневров.
Это удобно, поскольку это означает, что delta- v можно рассчитать и просто добавить, а соотношение масс вычислить только для всего транспортного средства для всей миссии. Таким образом, delta- v обычно указывается вместо соотношений масс, которые потребовали бы умножения.
Дельта-вбюджеты
При проектировании траектории бюджет delta- v используется как хороший индикатор того, сколько топлива потребуется. Расход топлива является экспоненциальной функцией delta- v в соответствии с уравнением ракеты , он также будет зависеть от скорости истечения.
Невозможно определить требования delta- v из закона сохранения энергии , рассматривая только полную энергию корабля на начальной и конечной орбитах, поскольку энергия уносится с выхлопом (см. также ниже). Например, большинство космических аппаратов запускаются на орбиту с наклонением, довольно близким к широте места запуска, чтобы использовать скорость вращения поверхности Земли. Если необходимо, по причинам, связанным с миссией, поместить космический аппарат на орбиту с другим наклонением , требуется существенная delta- v , хотя удельные кинетическая и потенциальная энергии на конечной орбите и начальной орбите равны.
Когда ракетная тяга применяется короткими импульсами, другие источники ускорения могут быть незначительны, и величина изменения скорости одного импульса может быть просто аппроксимирована дельта- v . Общая дельта- v, которая должна быть применена, может быть затем просто найдена путем сложения каждой из дельта- v, необходимых для дискретных импульсов, даже если между импульсами величина и направление скорости изменяются из-за гравитации, например, на эллиптической орбите .
Примеры расчета delta- v см . в Hohmann transfer orbit , gravitational slingshot и Interplanetary Transport Network . Также следует отметить, что большая тяга может уменьшить гравитационное сопротивление .
Delta- v также требуется для удержания спутников на орбите и расходуется на маневры поддержания орбитальной станции . Поскольку загрузка топлива на большинстве спутников не может быть пополнена, количество топлива, изначально загруженного на спутник, может определить его полезный срок службы.
эффект Оберта
Из соображений мощности получается, что при приложении дельта- v в направлении скорости удельная орбитальная энергия, получаемая на единицу дельта- v , равна мгновенной скорости. Это называется эффектом Оберта.
Например, спутник на эллиптической орбите разгоняется эффективнее на высокой скорости (то есть на малой высоте), чем на низкой скорости (то есть на большой высоте).
Другим примером является то, что когда транспортное средство пролетает мимо планеты, сжигание топлива при максимальном сближении, а не при более дальнем, обеспечивает значительно более высокую конечную скорость, и это тем более актуально, когда планета большая и имеет сильное гравитационное поле, например, Юпитер.
Участок свиной отбивной
Из-за того, что относительное положение планет меняется со временем, для разных дат запуска требуются разные delta-v. Диаграмма, которая показывает требуемую delta- v, построенную в зависимости от времени, иногда называется porkchop plot . Такая диаграмма полезна, поскольку позволяет рассчитать окно запуска , поскольку запуск должен происходить только тогда, когда миссия находится в пределах возможностей используемого транспортного средства. [4]
Вокруг Солнечной системы
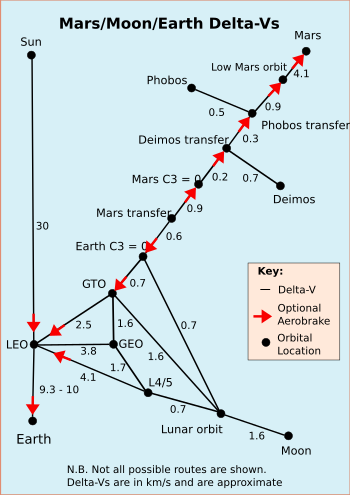
Delta- v, необходимая для различных орбитальных маневров с использованием обычных ракет; красные стрелки показывают, где может быть выполнено дополнительное аэродинамическое торможение в этом конкретном направлении, черные числа показывают delta- v в км/с, применимое в любом направлении. [5] [6] Передачи с более низким delta- v, чем показано, часто могут быть достигнуты, но включают редкие окна перехода или занимают значительно больше времени, см.: Орбитальная механика § Межпланетная транспортная сеть и нечеткие орбиты .
- С3
- Орбита побега
- ГЕО
- Геосинхронная орбита
- ГТО
- Геостационарная переходная орбита
- Л4/5
- Земля–Луна L 4 L 5 Точка Лагранжа
- ЛЕО
- Низкая околоземная орбита
возвращение на НОО
Например, космический корабль «Союз» совершает сход с орбиты МКС в два этапа. Сначала ему требуется delta- v 2,18 м/с для безопасного отделения от космической станции. Затем ему требуется еще 128 м/с для возвращения в атмосферу . [7]
Смотрите также
Ссылки
- ^ Саригуль-Клин, Несрин; Ноэль, Крис; Саригул-Клин, Мартинус (5 января 2004 г.). Транспортные средства с воздушным запуском с Земли на орбиту: Delta V выигрывает от условий запуска и аэродинамики транспортного средства. дои : 10.2514/6.2004-872. ISBN 9781624100789.
- ^ Это может иметь место в случае системы «продувки», в которой давление в баке понижается после использования топлива, и при этом уменьшается не только расход топлива, но и, в меньшей степени, скорость выхлопных газов .
- ^ Сила тяги на единицу массы равна где и являются заданными функциями времени .
- ^ "Исследование Марса: Особенности". marsprogram.jpl.nasa.gov .
- ^ "Ракеты и космический транспорт". Архивировано из оригинала 1 июля 2007 г. Получено 1 июня 2013 г.
- ^ "Delta-V Calculator". Архивировано из оригинала 12 марта 2000 года.Дает цифры 8,6 от поверхности Земли до LEO, 4,1 и 3,8 для LEO до лунной орбиты (или L5) и GEO соответственно, 0,7 для L5 до лунной орбиты и 2,2 для лунной орбиты до лунной поверхности. Цифры, как говорят, взяты из главы 2 книги Space Settlements: A Design Study, заархивированной 28 ноября 2001 г. в веб-архиве Библиотеки Конгресса на сайте NASA [ нерабочая ссылка ] .
- ↑ Гебхардт, Крис (17 апреля 2021 г.). «Союз МС-17 благополучно возвращает трех членов экипажа станции в Казахстан». nasaspaceflight.com . Получено 10 июля 2022 г. .

























