Делоне сет

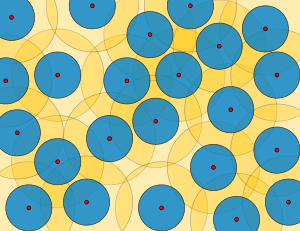
В математической теории метрических пространств ε - сети , ε -упаковки , ε -покрытия , равномерно дискретные множества , относительно плотные множества и множества Делоне (названные в честь Бориса Делоне ) — это несколько тесно связанных определений хорошо разнесенных множеств точек, а радиус упаковки и радиус покрытия этих множеств измеряют, насколько хорошо они разнесены. Эти множества имеют приложения в теории кодирования , алгоритмах аппроксимации и теории квазикристаллов .

Если ( M , d ) — метрическое пространство, а X — подмножество M , то радиус упаковки r множества X равен половине наименьшего расстояния между различными элементами X. Открытые шары радиуса r с центрами в точках X будут все не пересекаться. Радиус покрытия R множества X — это наименьшее расстояние, при котором каждая точка M находится на расстоянии R хотя бы от одной точки X ; то есть R — это наименьший радиус , при котором замкнутые шары этого радиуса с центрами в точках X имеют все M в качестве своего объединения.

ε -Упаковка — это множество X с радиусом упаковки r ≥ ⁠ ε/2⁠ (эквивалентно, минимальное расстояние ≥ ε ), ε -покрытие — это множество X с радиусом покрытия R ≤ ε , а ε -сеть — это множество, которое является как ε -упаковкой, так и ε -покрытием ( ⁠ ε/2⁠ ≤ r ≤ R ≤ ε ).

Множество равномерно дискретно , если оно имеет ненулевой радиус упаковки ( 0 < r ), и относительно плотно , если оно имеет конечный радиус покрытия ( R < ∞ ).

Множество Делоне — это множество, которое является как равномерно дискретным, так и относительно плотным ( 0 < r ≤ R < ∞ ). Таким образом, каждая ε -сеть является сетью Делоне, но не наоборот. ^{[1] [2]}

Как наиболее ограничительное из приведенных выше определений, ε -сети по крайней мере так же трудно построить, как ε -упаковки, ε -покрытия и множества Делоне. Однако всякий раз, когда точки M имеют хорошее упорядочение , трансфинитная индукция показывает, что можно построить ε -сеть N , включив в N каждую точку, для которой инфимум расстояний до множества более ранних точек в упорядочении составляет по крайней мере  ε . Для конечных множеств точек в евклидовом пространстве ограниченной размерности каждую точку можно проверить за постоянное время, отобразив ее в сетку ячеек диаметра ε и используя хэш-таблицу для проверки того, какие близлежащие ячейки уже содержат точки N ; таким образом, в этом случае ε -сеть можно построить за линейное время . ^{[3] [4]}

Для более общих конечных или компактных метрических пространств альтернативный алгоритм Тео Гонсалеса, основанный на обходе наиболее дальнего первого, может быть использован для построения конечной ε -сети. Этот алгоритм инициализирует сеть N пустой, а затем многократно добавляет к N самую дальнюю точку в M из N , разрывая связи произвольно и останавливаясь , когда все точки  M находятся на расстоянии  ε от  N. ^[5] В пространствах с ограниченной удвоенной размерностью алгоритм Гонсалеса может быть реализован за время O( n log n ) для множеств точек с полиномиальным отношением между их самым дальним и самым близким расстояниями и аппроксимирован за то же время для произвольных множеств точек. ^[6]

В теории кодов с исправлением ошибок метрическое пространство, содержащее блочный код C, состоит из строк фиксированной длины, скажем, n , взятых по алфавиту размера q (можно рассматривать как векторы ), с метрикой Хэмминга . Это пространство обозначается ⁠ ⁠${\displaystyle {\mathcal {A}}_{q}^{n}.}$ Радиус покрытия и радиус упаковки этого метрического пространства связаны со способностью кода исправлять ошибки. Примером может служить игра переключения Берлекэмпа .

Har-Peled & Raichel (2013) описывают алгоритмическую парадигму, которую они называют «net and prune» для разработки алгоритмов аппроксимации для определенных типов задач геометрической оптимизации, определенных на множествах точек в евклидовых пространствах . Алгоритм этого типа работает, выполняя следующие шаги:

1. Выберите случайную точку p из множества точек, найдите ее ближайшего соседа q и установите ε равным расстоянию между p и q .
2. Проверить, является ли ε (приблизительно) больше или меньше оптимального значения решения (используя методику, специфичную для конкретной решаемой задачи оптимизации)
   • Если больше, удалить из ввода точки, ближайший сосед которых находится дальше, чем ε
   • Если оно меньше, постройте ε -сеть N и удалите из входа точки, не входящие в N.

В обоих случаях ожидаемое количество оставшихся точек уменьшается на постоянный множитель, поэтому время доминирует на этапе тестирования. Как они показывают, эта парадигма может быть использована для построения быстрых алгоритмов аппроксимации для кластеризации k-центра , поиска пары точек со средним расстоянием и нескольких связанных проблем.

Иерархическая система сетей, называемая сетевым деревом , может использоваться в пространствах с ограниченной удвоенной размерностью для построения хорошо разделенных парных разложений , геометрических остовов и приближенных ближайших соседей . ^{[6] [7]}

Для точек в евклидовом пространстве множество X является множеством Мейера , если оно относительно плотное и его разностное множество X − X равномерно дискретно. Эквивалентно, X является множеством Мейера, если и X , и X − X являются множествами Делоне. Множества Мейера названы в честь Ива Мейера , который ввел их (с другим, но эквивалентным определением, основанным на гармоническом анализе ) в качестве математической модели для квазикристаллов . Они включают в себя точечные множества решеток , мозаики Пенроуза и суммы Минковского этих множеств с конечными множествами. ^[8]

Ячейки Вороного симметричных множеств Делоне образуют заполняющие пространство многогранники, называемые плезиоэдрами . ^[9]

• Delone set – Энциклопедия Tilings