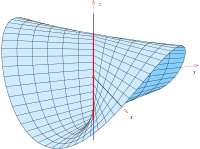
Коноид

В геометрии коноид (от греч. κωνος «  конус» и - ειδης  «подобный») — линейчатая поверхность , образующие (линии) которой удовлетворяют дополнительным условиям:

(1) Все линии параллельны плоскости , плоскости директрисы .

(2) Все линии пересекают фиксированную линию — ось .

Коноид является прямым коноидом , если его ось перпендикулярна его направляющей плоскости. Следовательно, все образующие перпендикулярны оси.

В силу (1) любой коноид является каталонской поверхностью и может быть параметрически представлен как

${\displaystyle \mathbf {x} (u,v)=\mathbf {c} (u)+v\mathbf {r} (u)\ }$

Любая кривая x ( u ₀ , v ) с фиксированным параметром u = u ₀ является направляющей, c ( u ) описывает направляющую , а векторы r ( u ) все параллельны плоскости направляющей. Плоскость векторов r ( u ) может быть представлена ​​как

${\displaystyle \det(\mathbf {r} ,\mathbf {\dot {r}} ,\mathbf {\ddot {r}} )=0}$.

Если директриса представляет собой окружность, то коноид называется круговым коноидом .

Термин «коноид» использовался ещё Архимедом в его трактате «О коноидах и сфероидах» .

Параметрическое представление

${\displaystyle \mathbf {x} (u,v)=(\cos u,\sin u,0)+v(0,-\sin u,z_{0})\ ,\ 0\leq u<2\ пи, v\in \mathbb {R} }$

описывает прямой круговой коноид с единичной окружностью плоскости xy в качестве направляющей и направляющей плоскостью, которая параллельна плоскости y--z. Его осью является прямая${\displaystyle (x,0,z_{0})\ x\in \mathbb {R} \ .}$

Особые характеристики :

1. Пересечение с горизонтальной плоскостью — эллипс.
2. ${\displaystyle (1-x^{2})(zz_{0})^{2}-y^{2}z_{0}^{2}=0}$является неявным представлением. Следовательно, прямой круговой коноид является поверхностью степени 4.
3. Правило Кеплера дает для прямого кругового коноида с радиусом и высотой точный объем: .${\displaystyle r}$${\displaystyle ч}$${\displaystyle V={\tfrac {\pi }{2}}r^{2}h}$

Неявное представление выполняется и точками прямой . Для этих точек не существует касательных плоскостей . Такие точки называются особыми .${\displaystyle (x,0,z_{0})}$

Параметрическое представление

${\displaystyle \mathbf {x} (u,v)=\left(1,u,-u^{2}\right)+v\left(-1,0,u^{2}\right)}$

${\displaystyle =\left(1-v,u,-(1-v)u^{2}\right)\ ,u,v\in \mathbb {R} \ ,}$

описывает параболический коноид с уравнением . Коноид имеет параболу в качестве направляющей, ось y в качестве оси и плоскость, параллельную плоскости xz, в качестве направляющей. Он используется архитекторами в качестве поверхности крыши (см. ниже).${\displaystyle z=-xy^{2}}$

Параболический коноид не имеет особых точек.

1. гиперболический параболоид
2. коноид Плюккера
3. Зонт Уитни
4. геликоид

• 
  гиперболический параболоид
• 
  коноид Плюккера
• 
  Зонтик Уитни

Существует множество коноидов с особыми точками, которые исследуются в алгебраической геометрии .

Как и другие линейчатые поверхности, коноиды представляют большой интерес для архитекторов, поскольку их можно построить с помощью балок или брусков. Правильные коноиды изготавливаются легко: нанизывают бруски на ось так, чтобы их можно было вращать только вокруг этой оси. Затем бруски отклоняют направляющей и получают коноид (параболический коноид).

• mathworld: коноид Плюккера
• «Коноид», Энциклопедия математики , EMS Press , 2001 [1994]

• А. Грей, Э. Аббена, С. Саламон, Современная дифференциальная геометрия кривых и поверхностей с Mathematica , 3-е изд. Boca Raton, FL:CRC Press, 2006. [1] ( ISBN 978-1-58488-448-4 ) 
• Владимир Я. Ровенский, Геометрия кривых и поверхностей с MAPLE [2] ( ISBN 978-0-8176-4074-3 )