Зонтик Уитни

В геометрии зонтик Уитни или зонтик Уитни , названный в честь американского математика Хасслера Уитни , и иногда называемый зонтиком Кэли , представляет собой специфическую самопересекающуюся линейчатую поверхность, расположенную в трех измерениях . Это объединение всех прямых линий , которые проходят через точки фиксированной параболы и перпендикулярны фиксированной прямой, которая параллельна оси параболы и лежит на ее перпендикулярной биссекторной плоскости.

Зонтик Уитни можно задать параметрическими уравнениями в декартовых координатах

${\displaystyle \left\{{\begin{align}x(u,v)&=uv,\\y(u,v)&=u,\\z(u,v)&=v^{2},\end{align}}\right.}$

где параметры u и v варьируются в пределах действительных чисел . Это также задается неявным уравнением

${\displaystyle x^{2}-y^{2}z=0.}$

Эта формула также включает отрицательную ось z (которая называется ручкой зонтика).

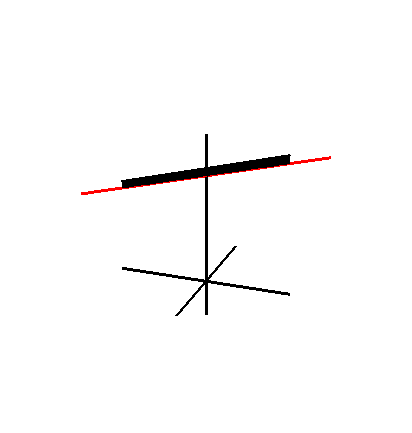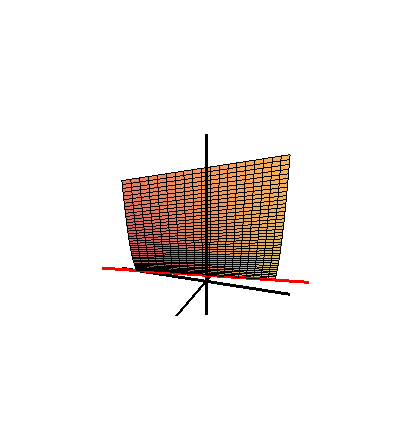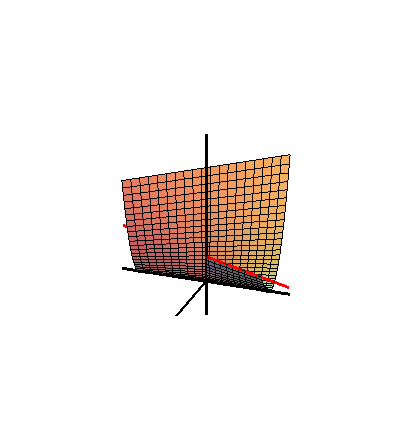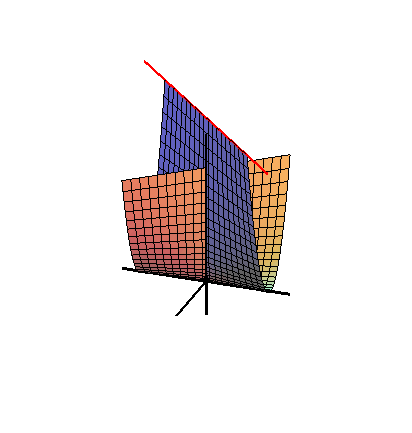
Зонтик Уитни — это линейчатая поверхность и прямой коноид . Он важен в области теории особенностей как простая локальная модель особенности точки защемления . Точка защемления и особенность складки — единственные устойчивые локальные особенности отображений из R ² в R ³ .

Назван в честь американского математика Хасслера Уитни .

В теории струн брана Уитни — это D7-брана, оборачивающая многообразие, сингулярности которого локально моделируются зонтиком Уитни. Браны Уитни появляются естественным образом при принятии предела слабой связи Сена F-теории .

• Кросс-колпачок
• Правый коноид
• Линейчатая поверхность

• «Зонтик Уитни». Топологический зоопарк . Центр геометрии . Получено 08.03.2006 .(Изображения и видео зонта Уитни.)