Изогнутое зеркало

Кривое зеркало — это зеркало с криволинейной отражающей поверхностью. Поверхность может быть выпуклой (выпуклой наружу) или вогнутой (утопленной внутрь). Большинство криволинейных зеркал имеют поверхности, имеющие форму части сферы , но в оптических устройствах иногда используются и другие формы. Наиболее распространенным несферическим типом являются параболические отражатели , которые используются в оптических устройствах, таких как отражательные телескопы , которым необходимо отображать удаленные объекты, поскольку сферические зеркальные системы, такие как сферические линзы , страдают от сферической аберрации . Кривые зеркала используются для развлечений. Они имеют выпуклые и вогнутые области, которые создают намеренно искаженные изображения. Они также обеспечивают сильно увеличенные или сильно уменьшенные (меньшие) изображения, когда объект находится на определенных расстояниях.
Выпуклые зеркала

Выпуклое зеркало или рассеивающее зеркало — это изогнутое зеркало, в котором отражающая поверхность выпячивается в сторону источника света. [1] Выпуклые зеркала отражают свет наружу, поэтому они не используются для фокусировки света. Такие зеркала всегда формируют мнимое изображение , поскольку фокусная точка ( F ) и центр кривизны ( 2F ) являются воображаемыми точками «внутри» зеркала, которые не могут быть достигнуты. В результате изображения, сформированные этими зеркалами, не могут быть спроецированы на экран, поскольку изображение находится внутри зеркала. Изображение меньше объекта, но становится больше по мере приближения объекта к зеркалу.
Коллимированный (параллельный) пучок света расходится (расширяется) после отражения от выпуклого зеркала, поскольку нормаль к поверхности различна в каждой точке зеркала.
Использование выпуклых зеркал

.jpg/440px-The_Arnolfini_Portrait,_détail_(2).jpg)
Зеркало со стороны пассажира в автомобиле обычно является выпуклым. В некоторых странах они маркируются предупреждением о безопасности « Объекты в зеркале ближе, чем кажутся », чтобы предупредить водителя об искажающем эффекте выпуклого зеркала на восприятие расстояния. Выпуклые зеркала предпочтительны в транспортных средствах, поскольку они дают прямое (не перевернутое), хотя и уменьшенное (меньшее) изображение, и поскольку они обеспечивают более широкое поле зрения, поскольку они изогнуты наружу.
Эти зеркала часто встречаются в коридорах различных зданий (обычно их называют «коридорными зеркалами безопасности»), включая больницы , гостиницы , школы , магазины и многоквартирные дома . Обычно их устанавливают на стене или потолке там, где коридоры пересекаются друг с другом или где они делают резкие повороты. Они полезны для людей, чтобы видеть любые препятствия, с которыми они столкнутся в следующем коридоре или после следующего поворота. Их также используют на дорогах , подъездных путях и переулках, чтобы обеспечить безопасность участников дорожного движения в местах с недостаточной видимостью, особенно на поворотах и изгибах. [2]
Выпуклые зеркала используются в некоторых банкоматах как простая и удобная функция безопасности, позволяющая пользователям видеть, что происходит за ними. Аналогичные устройства продаются для присоединения к обычным компьютерным мониторам . Выпуклые зеркала делают все визуально меньше, но покрывают большую область наблюдения.
Круглые выпуклые зеркала, называемые Oeil de Sorcière (по-французски «глаз колдуна»), были популярным предметом роскоши с 15-го века и далее, показаны на многих изображениях интерьеров того времени. [3] С технологиями 15-го века было легче сделать обычное изогнутое зеркало (из выдувного стекла), чем идеально плоское. Их также называли «глазами банкиров» из-за того, что их широкое поле зрения было полезно для безопасности. Известными примерами в искусстве являются « Портрет Арнольфини » Яна ван Эйка и левое крыло Верльского алтаря Роберта Кампена . [4]
Выпуклое зеркальное изображение

Изображение на выпуклом зеркале всегда мнимое ( лучи на самом деле не прошли сквозь изображение; их продолжения проходят, как в обычном зеркале), уменьшенное (меньшее) и прямое (не перевернутое). По мере приближения объекта к зеркалу изображение увеличивается, пока не достигнет приблизительно размера объекта, когда он коснется зеркала. По мере удаления объекта изображение уменьшается в размере и постепенно приближается к фокусу, пока не уменьшится до точки в фокусе, когда объект находится на бесконечном расстоянии. Эти особенности делают выпуклые зеркала очень полезными: поскольку в зеркале все кажется меньше, они охватывают более широкое поле зрения, чем обычное плоское зеркало , поэтому они полезны для наблюдения за автомобилями позади автомобиля водителя на дороге, наблюдения за более широкой областью для наблюдения и т. д.
Вогнутые зеркала

Вогнутое зеркало , или собирательное зеркало , имеет отражающую поверхность, которая утоплена внутрь (от падающего света). Вогнутые зеркала отражают свет внутрь к одной фокусной точке. Они используются для фокусировки света. В отличие от выпуклых зеркал, вогнутые зеркала показывают различные типы изображений в зависимости от расстояния между объектом и зеркалом.
Зеркала называются «сходящимися зеркалами», потому что они имеют тенденцию собирать свет, который падает на них, перефокусируя параллельные входящие лучи в направлении фокуса. Это происходит потому, что свет отражается под разными углами в разных точках зеркала, поскольку нормаль к поверхности зеркала отличается в каждой точке.
Использование вогнутых зеркал
Вогнутые зеркала используются в отражательных телескопах . [5] Они также используются для получения увеличенного изображения лица для нанесения макияжа или бритья. [6] В осветительных приложениях вогнутые зеркала используются для сбора света от небольшого источника и направления его наружу в виде луча, как в фонарях , фарах и прожекторах , или для сбора света с большой площади и фокусировки его в небольшое пятно, как в концентрированной солнечной энергии . Вогнутые зеркала используются для формирования оптических полостей , которые важны в лазерном строительстве . Некоторые стоматологические зеркала используют вогнутую поверхность для получения увеличенного изображения. Система помощи при посадке зеркал современных авианосцев также использует вогнутое зеркало.
Вогнутое зеркальное изображение
| Положение объекта ( S ), точка фокусировки ( F ) | Природа изображения | Диаграмма |
|---|---|---|
| (Объект между точкой фокусировки и зеркалом) |
|  |
| (Объект в фокусе) |
|  |
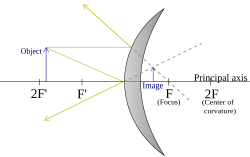
(Объект между фокусом и центром кривизны) |
| 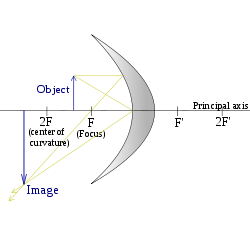 |
| (Объект в центре кривизны) |
|  |
(Объект за пределами центра кривизны) |
| 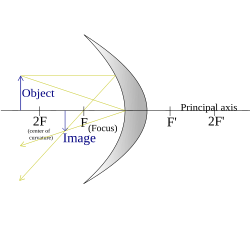 |
Зеркальная форма
Большинство изогнутых зеркал имеют сферический профиль. [7] Их проще всего изготовить, и это лучшая форма для общего применения. Однако сферические зеркала страдают от сферической аберрации — параллельные лучи, отраженные от таких зеркал, не фокусируются в одной точке. Для параллельных лучей, например, тех, которые исходят от очень удаленного объекта, параболический отражатель может сработать лучше. Такое зеркало может фокусировать входящие параллельные лучи в гораздо меньшее пятно, чем сферическое зеркало. Тороидальный отражатель — это форма параболического отражателя, которая имеет разное фокусное расстояние в зависимости от угла зеркала.
Анализ
Уравнение зеркала, увеличение и фокусное расстояние
Уравнение Гаусса зеркала, также известное как уравнение зеркала и линзы, связывает расстояние до объекта и расстояние до изображения с фокусным расстоянием : [2]
- .
Соглашение о знаках, используемое здесь, заключается в том, что фокусное расстояние положительно для вогнутых зеркал и отрицательно для выпуклых, а и положительны, когда объект и изображение находятся перед зеркалом соответственно. (Они положительны, когда объект или изображение являются реальными.) [2]
Для выпуклых зеркал, если переместить член в правую часть уравнения, чтобы решить для , то результатом всегда будет отрицательное число, что означает, что расстояние до изображения отрицательно — изображение является виртуальным, расположенным «позади» зеркала. Это согласуется с поведением, описанным выше.
Для вогнутых зеркал, является ли изображение мнимым или реальным, зависит от того, насколько велико расстояние до объекта по сравнению с фокусным расстоянием. Если член больше члена , то является положительным и изображение является реальным. В противном случае член отрицательный и изображение является мнимым. Опять же, это подтверждает поведение, описанное выше.
Увеличение зеркала определяется как высота изображения , деленная на высоту объекта:
- .
По соглашению, если полученное увеличение положительно, изображение прямое. Если увеличение отрицательное, изображение перевернуто (вверх ногами).
Трассировка лучей
Расположение и размер изображения также можно найти с помощью графической трассировки лучей, как показано на рисунках выше. Луч, проведенный от вершины объекта к вершине поверхности зеркала (где оптическая ось встречается с зеркалом), образует угол с оптической осью. Отраженный луч имеет тот же угол к оси, но с противоположной стороны (см. Зеркальное отражение ).
Второй луч можно провести из верхней части объекта параллельно оптической оси. Этот луч отражается зеркалом и проходит через его фокус. Точка, в которой встречаются эти два луча, является точкой изображения, соответствующей верхней части объекта. Ее расстояние от оптической оси определяет высоту изображения, а ее положение вдоль оси является положением изображения. Уравнение зеркала и уравнение увеличения можно вывести геометрически, рассмотрев эти два луча. Вместо этого можно рассмотреть луч, который идет из верхней части объекта через фокусную точку. Такой луч отражается параллельно оптической оси и также проходит через точку изображения, соответствующую верхней части объекта.
Матрица передачи лучей сферических зеркал
Математическая обработка выполняется в параксиальном приближении , что означает, что в первом приближении сферическое зеркало является параболическим отражателем . Матрица лучей вогнутого сферического зеркала показана здесь. Элемент матрицы равен , где — фокус оптического устройства.
В блоках 1 и 3 показано суммирование углов треугольника и сравнение с π радианами (или 180°). В блоке 2 показан ряд Маклорена до порядка 1. Выводы матриц лучей выпуклого сферического зеркала и тонкой линзы очень похожи.
Смотрите также
- Задача Альхазена (отражение от сферического зеркала)
- Анаморфоза
- Концентрированная солнечная энергия — метод получения солнечной энергии с использованием изогнутых зеркал или решеток зеркал.
- Список деталей и конструкции телескопа
Ссылки
- ^ Наяк, Санджай К.; Бхувана, К. П. (2012). Инженерная физика. Нью-Дели: Tata McGraw-Hill Education. стр. 6.4. ISBN 9781259006449.
- ^ abc Хехт, Юджин (1987). "5.4.3". Оптика (2-е изд.). Эддисон Уэсли. стр. 160–1. ISBN 0-201-11609-X.
- ^ Венеция Боттеге: антиквариат, бижутерия, кофе, пирожные, ковры, стекло Архивировано 06.03.2017 в Wayback Machine
- ^ Лорн Кэмпбелл, Каталоги Национальной галереи (новая серия): Голландская живопись пятнадцатого века , стр. 178-179, 188-189, 1998, ISBN 1-85709-171-X
- ^ Джоши, Дирен М. Живая научная физика 10. Ратна Сагар. ISBN 9788183322904. Архивировано из оригинала 2018-01-18.
- ^ Sura's Year Book 2006 (на английском языке). Sura Books. ISBN 9788172541248. Архивировано из оригинала 2018-01-18.
- ^ Аль-Аззави, Абдул (2006-12-26). Свет и оптика: принципы и практика. CRC Press. ISBN 9780849383144. Архивировано из оригинала 2018-01-18.
Внешние ссылки
- Java-апплеты для исследования трассировки лучей для изогнутых зеркал
- Вогнутые зеркала — реальные изображения, Molecular Expressions Optical Microscopy Primer
- Сферические зеркала, онлайн-лаборатория физики
- «Шлифовка самого большого в мире зеркала» Popular Science , декабрь 1935 г.