Функция ошибки

В математике функция ошибок (также называемая функцией ошибок Гаусса ), часто обозначаемая как erf , — это функция, определяемая как: ^[1]${\displaystyle \mathrm {erf} :\mathbb {C} \to \mathbb {C} }$$${\displaystyle \operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,\mathrm {d} t.}$$

Функция ошибки
График функции ошибки по действительным числам
Общая информация
Общее определение	${\displaystyle \operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\int _{0}^{z}e^{-t^{2}}\,\mathrm {d} t}$
Области применения	Вероятность, термодинамика, цифровая связь
Домен, кодомен и изображение
Домен	${\displaystyle \mathbb {C} }$
Изображение	${\displaystyle \left(-1,1\right)}$
Основные характеристики
Паритет	Странный
Особые черты
Корень	0
Производный	${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}e^{-z^{2}}}$
Первообразный	${\displaystyle \int \operatorname {erf} z\,dz=z\operatorname {erf} z+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}+C}$
Определение серии
ряд Тейлора	${\displaystyle \operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}{\frac {z^{2n+1}}{n!}}}$

Интеграл здесь является комплексным контурным интегралом, который не зависит от пути, поскольку является голоморфным на всей комплексной плоскости . Во многих приложениях аргумент функции является действительным числом, и в этом случае значение функции также является действительным.${\displaystyle \exp(-t^{2})}$${\displaystyle \mathbb {C} }$

В некоторых старых текстах ^[2] функция ошибки определяется без множителя . Этот неэлементарный интеграл является сигмоидальной функцией, которая часто встречается в теории вероятностей , статистике и уравнениях с частными производными . ${\displaystyle 2/{\sqrt {\pi }}}$

В статистике для неотрицательных действительных значений x функция ошибок имеет следующую интерпретацию: для действительной случайной величины Y , которая нормально распределена со средним значением 0 и стандартным отклонением , erf x представляет собой вероятность того, что Y попадает в диапазон [− x , x ] .${\displaystyle 1/{\sqrt {2}}}$

Две тесно связанные функции являются дополнительной функцией ошибки , определяемой как${\displaystyle \mathrm {erfc} :\mathbb {C} \to \mathbb {C} }$

$${\displaystyle \operatorname {erfc} z=1-\operatorname {erf} z,}$$

а мнимая функция ошибки определяется как${\displaystyle \mathrm {erfi} :\mathbb {C} \to \mathbb {C} }$

$${\displaystyle \operatorname {erfi} z=-i\operatorname {erf} iz,}$$

где i — мнимая единица .

Название «функция ошибки» и его сокращение erf были предложены Дж. В. Л. Глейшером в 1871 году из-за его связи с «теорией вероятности, и в частности с теорией ошибок ». ^[3] Дополнение функции ошибки также обсуждалось Глейшером в отдельной публикации в том же году. ^[4] Для «закона легкости» ошибок, плотность которых задается выражением ( нормальное распределение ), Глейшер вычисляет вероятность ошибки, лежащей между p и q, как:$${\displaystyle f(x)=\left({\frac {c}{\pi }}\right)^{1/2}e^{-cx^{2}}}$$$${\displaystyle \left({\frac {c}{\pi }}\right)^{\frac {1}{2}}\int _{p}^{q}e^{-cx^{2}}\,\mathrm {d} x={\tfrac {1}{2}}\left(\operatorname {erf} \left(q{\sqrt {c}}\right)-\operatorname {erf} \left(p{\sqrt {c}}\right)\right).}$$

Когда результаты серии измерений описываются нормальным распределением со стандартным отклонением σ и ожидаемым значением 0, то erf ( ⁠а/σ √ 2⁠ ) ​​— вероятность того, что ошибка отдельного измерения лежит между − a и + a , для положительного a . Это полезно, например, при определении частоты ошибок в битах цифровой системы связи.

Функции ошибок и дополнительные функции ошибок возникают, например, в решениях уравнения теплопроводности , когда граничные условия задаются ступенчатой ​​функцией Хевисайда .

Функцию ошибки и ее приближения можно использовать для оценки результатов, которые выполняются с высокой или низкой вероятностью. При наличии случайной величины X ~ Norm[ μ , σ ] (нормальное распределение со средним значением μ и стандартным отклонением σ ) и константы L > μ , ее можно показать с помощью интегрирования путем подстановки:$${\displaystyle {\begin{aligned}\Pr[X\leq L]&={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} {\frac {L-\mu }{{\sqrt {2}}\sigma }}\\&\approx A\exp \left(-B\left({\frac {L-\mu }{\sigma }}\right)^{2}\right)\end{aligned}}}$$

где A и B — некоторые числовые константы. Если L достаточно далеко от среднего значения, а именно μ − L ≥ σ √ ln k , то:

$${\displaystyle \Pr[X\leq L]\leq A\exp(-B\ln {k})={\frac {A}{k^{B}}}}$$

поэтому вероятность стремится к 0 при k → ∞ .

Вероятность нахождения X в интервале [ L _a , L _b ] можно вывести как$${\displaystyle {\begin{aligned}\Pr[L_{a}\leq X\leq L_{b}]&=\int _{L_{a}}^{L_{b}}{\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x\\&={\frac {1}{2}}\left(\operatorname {erf} {\frac {L_{b}-\mu }{{\sqrt {2}}\sigma }}-\operatorname {erf} {\frac {L_{a}-\mu }{{\sqrt {2}}\sigma }}\right).\end{aligned}}}$$

Свойство erf (− z ) = −erf z означает, что функция ошибки является нечетной функцией . Это напрямую следует из того факта, что подынтегральное выражение e ^{− t 2} является четной функцией (первообразная четной функции, равная нулю в начале координат, является нечетной функцией и наоборот).

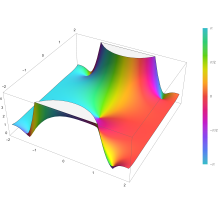
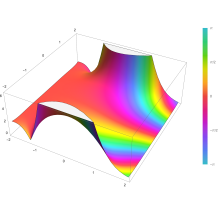
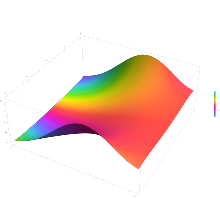
Так как функция ошибки является целой функцией , которая переводит действительные числа в действительные числа, для любого комплексного числа z : где z — комплексно сопряженное число z .$${\displaystyle \operatorname {erf} {\overline {z}}={\overline {\operatorname {erf} z}}}$$

Подынтегральные функции f = exp(− z ² ) и f = erf z показаны в комплексной z -плоскости на рисунках справа с раскраской доменов .

Функция ошибки при +∞ равна точно 1 (см. Гауссовский интеграл ). На действительной оси erf z стремится к единице при z → +∞ и к −1 при z → −∞ . На мнимой оси она стремится к ± i ∞ .

Функция ошибки является целой функцией ; она не имеет сингулярностей (кроме бесконечности) и ее разложение Тейлора всегда сходится. Однако при x >> 1 сокращение ведущих членов делает разложение Тейлора непрактичным.

Определяющий интеграл не может быть оценен в замкнутой форме в терминах элементарных функций (см. теорему Лиувилля ), но, разлагая подынтегральное выражение e ^{− z 2} в ряд Маклорена и интегрируя почленно, получаем ряд Маклорена функции ошибки как: что справедливо для любого комплексного числа z . Знаменатели — это последовательность A007680 в OEIS .$${\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\cdots \right)\end{aligned}}}$$ 

Для итеративного расчета вышеуказанного ряда может оказаться полезной следующая альтернативная формулировка: поскольку ⁠$${\displaystyle {\begin{aligned}\operatorname {erf} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)\\[6pt]&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}\end{aligned}}}$$−(2k − ¹ ) z2/к (2 к + 1)⁠ выражает множитель, превращающий k -й член в ( k  + 1) -й член (рассматривая z как первый член).

Мнимая функция ошибки имеет очень похожий ряд Маклорена, который имеет вид: который справедлив для любого комплексного числа z .$${\displaystyle {\begin{aligned}\operatorname {erfi} z&={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{n!(2n+1)}}\\[6pt]&={\frac {2}{\sqrt {\pi }}}\left(z+{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}+{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}+\cdots \right)\end{aligned}}}$$ 

Производная функции ошибки непосредственно следует из ее определения: Отсюда производная мнимой функции ошибки также непосредственно следует: Первообразная функции ошибки, получаемая интегрированием по частям , равна Первообразная мнимой функции ошибки, также получаемая интегрированием по частям, равна Производные более высокого порядка задаются выражением где H — физические полиномы Эрмита . ^[5]$${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {erf} z={\frac {2}{\sqrt {\pi }}}e^{-z^{2}}.}$$$${\displaystyle {\frac {d}{dz}}\operatorname {erfi} z={\frac {2}{\sqrt {\pi }}}e^{z^{2}}.}$$$${\displaystyle z\operatorname {erf} z+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}.}$$$${\displaystyle z\operatorname {erfi} z-{\frac {e^{z^{2}}}{\sqrt {\pi }}}.}$$$${\displaystyle \operatorname {erf} ^{(k)}z={\frac {2(-1)^{k-1}}{\sqrt {\pi }}}{\mathit {H}}_{k-1}(z)e^{-z^{2}}={\frac {2}{\sqrt {\pi }}}{\frac {\mathrm {d} ^{k-1}}{\mathrm {d} z^{k-1}}}\left(e^{-z^{2}}\right),\qquad k=1,2,\dots }$$

Разложение, ^[6] которое сходится быстрее для всех действительных значений x, чем разложение Тейлора, получается с использованием теоремы Ганса Генриха Бюрмана : ^[7] где sgn — знаковая функция . Сохраняя только первые два коэффициента и выбирая c ₁ = ⁠$${\displaystyle {\begin{aligned}\operatorname {erf} x&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left(1-{\frac {1}{12}}\left(1-e^{-x^{2}}\right)-{\frac {7}{480}}\left(1-e^{-x^{2}}\right)^{2}-{\frac {5}{896}}\left(1-e^{-x^{2}}\right)^{3}-{\frac {787}{276480}}\left(1-e^{-x^{2}}\right)^{4}-\cdots \right)\\[10pt]&={\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+\sum _{k=1}^{\infty }c_{k}e^{-kx^{2}}\right).\end{aligned}}}$$31/200⁠ и с ₂ = − ⁠341/8000⁠ , полученное приближение показывает наибольшую относительную ошибку при x = ±1,3796 , где она меньше 0,0036127:$${\displaystyle \operatorname {erf} x\approx {\frac {2}{\sqrt {\pi }}}\operatorname {sgn} x\cdot {\sqrt {1-e^{-x^{2}}}}\left({\frac {\sqrt {\pi }}{2}}+{\frac {31}{200}}e^{-x^{2}}-{\frac {341}{8000}}e^{-2x^{2}}\right).}$$

При наличии комплексного числа z не существует уникального комплексного числа w, удовлетворяющего erf w = z , поэтому истинная обратная функция будет многозначной. Однако для −1 < x < 1 существует уникальное действительное число, обозначенное erf ⁻¹ x, удовлетворяющее$${\displaystyle \operatorname {erf} \left(\operatorname {erf} ^{-1}x\right)=x.}$$

Обратная функция ошибки обычно определяется с областью (−1,1) и ограничена этой областью во многих системах компьютерной алгебры. Однако ее можно расширить до круга | z | < 1 комплексной плоскости, используя ряд Маклорена ^[8] , где c ₀ = 1 и$${\displaystyle \operatorname {erf} ^{-1}z=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},}$$$${\displaystyle {\begin{aligned}c_{k}&=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}\\[1ex]&=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},{\frac {4369}{2520}},{\frac {34807}{16200}},\ldots \right\}.\end{aligned}}}$$

Итак, мы имеем разложение ряда (общие множители были сокращены из числителей и знаменателей): (После сокращения значения числителя и знаменателя в OEIS : A092676 и OEIS : A092677 соответственно; без сокращения члены числителя являются значениями в OEIS : A002067 .) Значение функции ошибки при  ±∞ равно  ±1 .$${\displaystyle \operatorname {erf} ^{-1}z={\frac {\sqrt {\pi }}{2}}\left(z+{\frac {\pi }{12}}z^{3}+{\frac {7\pi ^{2}}{480}}z^{5}+{\frac {127\pi ^{3}}{40320}}z^{7}+{\frac {4369\pi ^{4}}{5806080}}z^{9}+{\frac {34807\pi ^{5}}{182476800}}z^{11}+\cdots \right).}$$

Для | z | < 1 имеем erf(erf ⁻¹ z ) = z .

Обратная дополнительная функция ошибки определяется как Для действительного x существует уникальное действительное число erfi ⁻¹ x , удовлетворяющее erfi(erfi ⁻¹ x ) = x . Обратная мнимая функция ошибки определяется как erfi ⁻¹ x . ^[9]$${\displaystyle \operatorname {erfc} ^{-1}(1-z)=\operatorname {erf} ^{-1}z.}$$

Для любого действительного x можно использовать метод Ньютона для вычисления erfi ⁻¹ x , а для −1 ≤ x ≤ 1 сходится следующий ряд Маклорена: где c _k определено, как указано выше.$${\displaystyle \operatorname {erfi} ^{-1}z=\sum _{k=0}^{\infty }{\frac {(-1)^{k}c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},}$$

Полезное асимптотическое разложение дополнительной функции ошибки (и, следовательно, также функции ошибки) для больших действительных x имеет вид , где (2 n − 1)!! — двойной факториал ( 2 n − 1) , который является произведением всех нечетных чисел до (2 n − 1) . Этот ряд расходится для любого конечного x , и его смысл как асимптотического разложения состоит в том, что для любого целого числа N ≥ 1 имеем , где остаток равен , что легко следует из индукции, записи и интегрирования по частям.$${\displaystyle {\begin{aligned}\operatorname {erfc} x&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left(1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{\left(2x^{2}\right)^{n}}}\right)\\[6pt]&={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}},\end{aligned}}}$$$${\displaystyle \operatorname {erfc} x={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{N-1}(-1)^{n}{\frac {(2n-1)!!}{\left(2x^{2}\right)^{n}}}+R_{N}(x)}$$$${\displaystyle R_{N}(x):={\frac {(-1)^{N}}{\sqrt {\pi }}}2^{1-2N}{\frac {(2N)!}{N!}}\int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,\mathrm {d} t,}$$$${\displaystyle e^{-t^{2}}=-(2t)^{-1}\left(e^{-t^{2}}\right)'}$$

Асимптотическое поведение остаточного члена в обозначениях Ландау имеет вид x → ∞ . Это можно найти по формуле Для достаточно больших значений x для получения хорошего приближения erfc x необходимы только первые несколько членов этого асимптотического разложения (в то время как для не слишком больших значений x приведенное выше разложение Тейлора в точке 0 обеспечивает очень быструю сходимость).$${\displaystyle R_{N}(x)=O\left(x^{-(1+2N)}e^{-x^{2}}\right)}$$$${\displaystyle R_{N}(x)\propto \int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,\mathrm {d} t=e^{-x^{2}}\int _{0}^{\infty }(t+x)^{-2N}e^{-t^{2}-2tx}\,\mathrm {d} t\leq e^{-x^{2}}\int _{0}^{\infty }x^{-2N}e^{-2tx}\,\mathrm {d} t\propto x^{-(1+2N)}e^{-x^{2}}.}$$

Разложение в непрерывную дробь дополнительной функции ошибок было найдено Лапласом : [ ^{10] [11]}$${\displaystyle \operatorname {erfc} z={\frac {z}{\sqrt {\pi }}}e^{-z^{2}}{\cfrac {1}{z^{2}+{\cfrac {a_{1}}{1+{\cfrac {a_{2}}{z^{2}+{\cfrac {a_{3}}{1+\dotsb }}}}}}}},\qquad a_{m}={\frac {m}{2}}.}$$

Обратный факториальный ряд: сходится при Re( z ² ) > 0 . Здесь z ⁿ обозначает растущий факториал , а s ( n , k ) обозначает знаковое число Стирлинга первого рода . ^{[12] [13]} Существует также представление бесконечной суммой, содержащей двойной факториал :$${\displaystyle {\begin{aligned}\operatorname {erfc} z&={\frac {e^{-z^{2}}}{{\sqrt {\pi }}\,z}}\sum _{n=0}^{\infty }{\frac {\left(-1\right)^{n}Q_{n}}{{\left(z^{2}+1\right)}^{\bar {n}}}}\\[1ex]&={\frac {e^{-z^{2}}}{{\sqrt {\pi }}\,z}}\left[1-{\frac {1}{2}}{\frac {1}{(z^{2}+1)}}+{\frac {1}{4}}{\frac {1}{\left(z^{2}+1\right)\left(z^{2}+2\right)}}-\cdots \right]\end{aligned}}}$$$${\displaystyle {\begin{aligned}Q_{n}&{\overset {\text{def}}{{}={}}}{\frac {1}{\Gamma {\left({\frac {1}{2}}\right)}}}\int _{0}^{\infty }\tau (\tau -1)\cdots (\tau -n+1)\tau ^{-{\frac {1}{2}}}e^{-\tau }\,d\tau \\[1ex]&=\sum _{k=0}^{n}\left({\frac {1}{2}}\right)^{\bar {k}}s(n,k),\end{aligned}}}$$$${\displaystyle \operatorname {erf} z={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-2)^{n}(2n-1)!!}{(2n+1)!}}z^{2n+1}}$$

• Абрамовиц и Стиган дают несколько приближений различной точности (уравнения 7.1.25–28). Это позволяет выбрать самое быстрое приближение, подходящее для данного приложения. В порядке возрастания точности они следующие: (максимальная ошибка:$${\displaystyle \operatorname {erf} x\approx 1-{\frac {1}{\left(1+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}\right)^{4}}},\qquad x\geq 0}$$5 × 10−4 )^​

  где а ₁ = 0,278393 , а ₂ = 0,230389 , а ₃ = 0,000972 , а ₄ = 0,078108

  $${\displaystyle \operatorname {erf} x\approx 1-\left(a_{1}t+a_{2}t^{2}+a_{3}t^{3}\right)e^{-x^{2}},\quad t={\frac {1}{1+px}},\qquad x\geq 0}$$(максимальная ошибка:2,5 × 10−5 )^​

  где p = 0,47047 , a ₁ = 0,3480242 , a ₂ = −0,0958798 , a ₃ = 0,7478556

  $${\displaystyle \operatorname {erf} x\approx 1-{\frac {1}{\left(1+a_{1}x+a_{2}x^{2}+\cdots +a_{6}x^{6}\right)^{16}}},\qquad x\geq 0}$$(максимальная ошибка:3 × 10−7 )^​

  где а ₁ = 0,0705230784 , а ₂ = 0,0422820123 , а ₃ = 0,0092705272 , а ₄ = 0,0001520143 , а ₅ = 0,0002765672 , а ₆ = 0,0000430638

  $${\displaystyle \operatorname {erf} x\approx 1-\left(a_{1}t+a_{2}t^{2}+\cdots +a_{5}t^{5}\right)e^{-x^{2}},\quad t={\frac {1}{1+px}}}$$(максимальная ошибка:1,5 × 10−7 )^​

  где p = 0,3275911 , a ₁ = 0,254829592 , a ₂ = −0,284496736 , a ₃ = 1,421413741 , a ₄ = −1,453152027 , a ₅ = 1,061405429

  Все эти приближения справедливы для x ≥ 0. Чтобы использовать эти приближения для отрицательных x , воспользуйтесь тем фактом, что erf x является нечетной функцией, поэтому erf x = −erf(− x ) .

• Экспоненциальные границы и чисто экспоненциальное приближение для дополнительной функции ошибок определяются формулой ^[14]$${\displaystyle {\begin{aligned}\operatorname {erfc} x&\leq {\frac {1}{2}}e^{-2x^{2}}+{\frac {1}{2}}e^{-x^{2}}\leq e^{-x^{2}},&\quad x&>0\\[1.5ex]\operatorname {erfc} x&\approx {\frac {1}{6}}e^{-x^{2}}+{\frac {1}{2}}e^{-{\frac {4}{3}}x^{2}},&\quad x&>0.\end{aligned}}}$$
• Вышеизложенное было обобщено до сумм N экспонент ^[15] с возрастающей точностью в терминах N, так что erfc x может быть точно аппроксимировано или ограничено 2 Q̃ ( √ 2 x ) , где В частности, существует систематическая методология для решения числовых коэффициентов {( a _n , b _n )}$${\displaystyle {\tilde {Q}}(x)=\sum _{n=1}^{N}a_{n}e^{-b_{n}x^{2}}.}$$^N
  _{н = 1}которые дают минимаксное приближение или границу для тесно связанной Q-функции : Q ( x ) ≈ Q̃ ( x ) , Q ( x ) ≤ Q̃ ( x ) или Q ( x ) ≥ Q̃ ( x ) для x ≥ 0. Коэффициенты {( a _n , b _n )}^N
  _{н = 1}для многих вариаций экспоненциальных приближений и границ до N = 25 был опубликован открытый доступ в качестве всеобъемлющего набора данных. ^[16]
• Плотное приближение дополнительной функции ошибок для x ∈ [0,∞) дано Карагианнидисом и Лиумпасом (2007) ^[17], которые показали для соответствующего выбора параметров { A , B } , что Они определили { A , B } = {1,98,1,135} , что дало хорошее приближение для всех x ≥ 0. Альтернативные коэффициенты также доступны для настройки точности для конкретного приложения или преобразования выражения в плотную границу. ^[18]$${\displaystyle \operatorname {erfc} x\approx {\frac {\left(1-e^{-Ax}\right)e^{-x^{2}}}{B{\sqrt {\pi }}x}}.}$$
• Нижняя граница с одним членом ^[19] позволяет выбрать параметр β для минимизации ошибки на желаемом интервале аппроксимации.$${\displaystyle \operatorname {erfc} x\geq {\sqrt {\frac {2e}{\pi }}}{\frac {\sqrt {\beta -1}}{\beta }}e^{-\beta x^{2}},\qquad x\geq 0,\quad \beta >1,}$$
• Другое приближение дано Сергеем Виницким с использованием его «глобальных приближений Паде»: ^{[20] [21] : 2–3} где Это разработано так, чтобы быть очень точным в окрестности 0 и окрестности бесконечности, а относительная погрешность составляет менее 0,00035 для всех действительных x . Использование альтернативного значения a ≈ 0,147 снижает максимальную относительную погрешность примерно до 0,00013. ^[22]$${\displaystyle \operatorname {erf} x\approx \operatorname {sgn} x\cdot {\sqrt {1-\exp \left(-x^{2}{\frac {{\frac {4}{\pi }}+ax^{2}}{1+ax^{2}}}\right)}}}$$$${\displaystyle a={\frac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0.140012.}$$

  Это приближение можно инвертировать, чтобы получить приближение для обратной функции ошибки:$${\displaystyle \operatorname {erf} ^{-1}x\approx \operatorname {sgn} x\cdot {\sqrt {{\sqrt {\left({\frac {2}{\pi a}}+{\frac {\ln \left(1-x^{2}\right)}{2}}\right)^{2}-{\frac {\ln \left(1-x^{2}\right)}{a}}}}-\left({\frac {2}{\pi a}}+{\frac {\ln \left(1-x^{2}\right)}{2}}\right)}}.}$$

• Приближение с максимальной погрешностью1,2 × 10 ⁻⁷ для любого действительного аргумента равно: ^[23] с и$${\displaystyle \operatorname {erf} x={\begin{cases}1-\tau &x\geq 0\\\tau -1&x<0\end{cases}}}$$$${\displaystyle {\begin{aligned}\tau &=t\cdot \exp \left(-x^{2}-1.26551223+1.00002368t+0.37409196t^{2}+0.09678418t^{3}-0.18628806t^{4}\right.\\&\left.\qquad \qquad \qquad +0.27886807t^{5}-1.13520398t^{6}+1.48851587t^{7}-0.82215223t^{8}+0.17087277t^{9}\right)\end{aligned}}}$$$${\displaystyle t={\frac {1}{1+{\frac {1}{2}}|x|}}.}$$
• Приближение с максимальной относительной погрешностью, меньшей по абсолютной величине, равно: ^[24] для , и для${\displaystyle \operatorname {erfc} }$${\displaystyle 2^{-53}}$ ${\displaystyle \left(\approx 1.1\times 10^{-16}\right)}$${\displaystyle x\geq 0}$$${\displaystyle {\begin{aligned}\operatorname {erfc} \left(x\right)&=\left({\frac {0.56418958354775629}{x+2.06955023132914151}}\right)\left({\frac {x^{2}+2.71078540045147805x+5.80755613130301624}{x^{2}+3.47954057099518960x+12.06166887286239555}}\right)\\&\left({\frac {x^{2}+3.47469513777439592x+12.07402036406381411}{x^{2}+3.72068443960225092x+8.44319781003968454}}\right)\left({\frac {x^{2}+4.00561509202259545x+9.30596659485887898}{x^{2}+3.90225704029924078x+6.36161630953880464}}\right)\\&\left({\frac {x^{2}+5.16722705817812584x+9.12661617673673262}{x^{2}+4.03296893109262491x+5.13578530585681539}}\right)\left({\frac {x^{2}+5.95908795446633271x+9.19435612886969243}{x^{2}+4.11240942957450885x+4.48640329523408675}}\right)e^{-x^{2}}\\\end{aligned}}}$$${\displaystyle x<0}$$${\displaystyle \operatorname {erfc} \left(x\right)=2-\operatorname {erfc} \left(-x\right)}$$
• Простую аппроксимацию для действительных аргументов можно выполнить с помощью гиперболических функций : которые сохраняют абсолютную разность .$${\displaystyle \operatorname {erf} \left(x\right)\approx z(x)=\tanh \left({\frac {2}{\sqrt {\pi }}}\left(x+{\frac {11}{123}}x^{3}\right)\right)}$$${\displaystyle \left|\operatorname {erf} \left(x\right)-z(x)\right|<0.000358,\,\forall x}$

Дополнительная функция ошибок , обозначаемая erfc , определяется как

$${\displaystyle {\begin{aligned}\operatorname {erfc} x&=1-\operatorname {erf} x\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\\[5pt]&=e^{-x^{2}}\operatorname {erfcx} x,\end{aligned}}}$$которая также определяет erfcx , масштабированную дополнительную функцию ошибок ^[25] (которую можно использовать вместо erfc для избежания арифметической потери значимости ^{[25] [26]} ). Другая форма erfc x для x ≥ 0 известна как формула Крейга, в честь ее первооткрывателя: ^[27] Это выражение справедливо только для положительных значений x , но его можно использовать вместе с erfc x = 2 − erfc(− x ) для получения erfc( x ) для отрицательных значений. Эта форма выгодна тем, что диапазон интегрирования фиксирован и конечен. Расширение этого выражения для erfc суммы двух неотрицательных переменных выглядит следующим образом: ^[28]$${\displaystyle \operatorname {erfc} (x\mid x\geq 0)={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{\sin ^{2}\theta }}\right)\,\mathrm {d} \theta .}$$$${\displaystyle \operatorname {erfc} (x+y\mid x,y\geq 0)={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\exp \left(-{\frac {x^{2}}{\sin ^{2}\theta }}-{\frac {y^{2}}{\cos ^{2}\theta }}\right)\,\mathrm {d} \theta .}$$

Мнимая функция ошибки , обозначаемая erfi , определяется как

$${\displaystyle {\begin{aligned}\operatorname {erfi} x&=-i\operatorname {erf} ix\\[5pt]&={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{t^{2}}\,\mathrm {d} t\\[5pt]&={\frac {2}{\sqrt {\pi }}}e^{x^{2}}D(x),\end{aligned}}}$$где D ( x ) — функция Доусона (которую можно использовать вместо erfi , чтобы избежать арифметического переполнения ^[25] ).

Несмотря на название «мнимая функция ошибок», erfi x является действительным числом, когда x является действительным.

Когда функция ошибки оценивается для произвольных комплексных аргументов z , результирующая комплексная функция ошибки обычно обсуждается в масштабированной форме как функция Фаддеева :$${\displaystyle w(z)=e^{-z^{2}}\operatorname {erfc} (-iz)=\operatorname {erfcx} (-iz).}$$

Функция ошибки по сути идентична стандартной нормальной кумулятивной функции распределения , обозначаемой Φ , также называемой norm( x ) некоторыми языками программирования ^{[ требуется ссылка ]} , поскольку они отличаются только масштабированием и переводом. Действительно,

$${\displaystyle {\begin{aligned}\Phi (x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t\\[6pt]&={\frac {1}{2}}\left(1+\operatorname {erf} {\frac {x}{\sqrt {2}}}\right)\\[6pt]&={\frac {1}{2}}\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)\end{aligned}}}$$или переставлено для erf и erfc :$${\displaystyle {\begin{aligned}\operatorname {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\[6pt]\operatorname {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)\\&=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}}$$

Следовательно, функция ошибки также тесно связана с Q-функцией , которая является хвостовой вероятностью стандартного нормального распределения. Q-функция может быть выражена через функцию ошибки как$${\displaystyle {\begin{aligned}Q(x)&={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} {\frac {x}{\sqrt {2}}}\\&={\frac {1}{2}}\operatorname {erfc} {\frac {x}{\sqrt {2}}}.\end{aligned}}}$$

Обратная функция Φ известна как нормальная квантильная функция или пробит -функция и может быть выражена через обратную функцию ошибок следующим образом:$${\displaystyle \operatorname {probit} (p)=\Phi ^{-1}(p)={\sqrt {2}}\operatorname {erf} ^{-1}(2p-1)=-{\sqrt {2}}\operatorname {erfc} ^{-1}(2p).}$$

Стандартная нормальная функция распределения чаще используется в теории вероятностей и статистике, а функция ошибок — в других разделах математики.

Функция ошибок является частным случаем функции Миттаг-Леффлера и может быть также выражена как конфлюэнтная гипергеометрическая функция (функция Куммера):$${\displaystyle \operatorname {erf} x={\frac {2x}{\sqrt {\pi }}}M\left({\tfrac {1}{2}},{\tfrac {3}{2}},-x^{2}\right).}$$

Это имеет простое выражение в терминах интеграла Френеля . ^{[ необходимо дальнейшее объяснение ]}

В терминах регуляризованной гамма-функции P и неполной гамма-функции sgn x является знаковой функцией .$${\displaystyle \operatorname {erf} x=\operatorname {sgn} x\cdot P\left({\tfrac {1}{2}},x^{2}\right)={\frac {\operatorname {sgn} x}{\sqrt {\pi }}}\gamma {\left({\tfrac {1}{2}},x^{2}\right)}.}$$

Повторные интегралы дополнительной функции ошибок определяются как ^[29]$${\displaystyle {\begin{aligned}i^{n}\!\operatorname {erfc} z&=\int _{z}^{\infty }i^{n-1}\!\operatorname {erfc} \zeta \,\mathrm {d} \zeta \\[6pt]i^{0}\!\operatorname {erfc} z&=\operatorname {erfc} z\\i^{1}\!\operatorname {erfc} z&=\operatorname {ierfc} z={\frac {1}{\sqrt {\pi }}}e^{-z^{2}}-z\operatorname {erfc} z\\i^{2}\!\operatorname {erfc} z&={\tfrac {1}{4}}\left(\operatorname {erfc} z-2z\operatorname {ierfc} z\right)\\\end{aligned}}}$$

Общая рекуррентная формула имеет вид$${\displaystyle 2n\cdot i^{n}\!\operatorname {erfc} z=i^{n-2}\!\operatorname {erfc} z-2z\cdot i^{n-1}\!\operatorname {erfc} z}$$

Они имеют степенной ряд , из которого следуют свойства симметрии и$${\displaystyle i^{n}\!\operatorname {erfc} z=\sum _{j=0}^{\infty }{\frac {(-z)^{j}}{2^{n-j}j!\,\Gamma \left(1+{\frac {n-j}{2}}\right)}},}$$$${\displaystyle i^{2m}\!\operatorname {erfc} (-z)=-i^{2m}\!\operatorname {erfc} z+\sum _{q=0}^{m}{\frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}}$$$${\displaystyle i^{2m+1}\!\operatorname {erfc} (-z)=i^{2m+1}\!\operatorname {erfc} z+\sum _{q=0}^{m}{\frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}.}$$

• В операционных системах, совместимых с POSIX , заголовок math.hдолжен объявлять, а математическая библиотека libmдолжна предоставлять функции erfи erfc( двойной точности ), а также их аналоги с одинарной и расширенной точностьюerff , erflи erfcf,. ^[30erfcl ]
• Научная библиотека GNU предоставляет функции erfошибок , erfc, log(erf), и масштабированные функции ошибок. ^[31]

• libcerf, числовая библиотека C для комплексных функций ошибок, предоставляет комплексные функции cerf, cerfc, cerfcxи действительные функции erfiс erfcxточностью приблизительно 13–14 цифр на основе функции Фаддеевой , реализованной в пакете MIT Faddeeva

• Abramowitz, Milton ; Stegun, Irene Ann , ред. (1983) [июнь 1964]. "Глава 7". Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия Applied Mathematics. Том 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. стр. 297. ISBN 978-0-486-61272-0. LCCN  64-60036. MR  0167642. LCCN  65-12253.
• Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), «Раздел 6.2. Неполная гамма-функция и функция ошибок», Numerical Recipes: The Art of Scientific Computing (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8, заархивировано из оригинала 11 августа 2011 г. , извлечено 9 августа 2011 г.
• Темме, Нико М. (2010), «Функции ошибок, интегралы Доусона и Френеля», в Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (ред.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, г-н  2723248.

• Таблица интегралов функций ошибок