Теория полиэдральных скелетных электронных пар
В химии теория полиэдральных скелетных электронных пар (PSEPT) предоставляет правила подсчета электронов, полезные для прогнозирования структур кластеров , таких как кластеры борана и карборана . Правила подсчета электронов были первоначально сформулированы Кеннетом Уэйдом [ 1] и были далее развиты другими, включая Майкла Мингоса [2] ; иногда их называют правилами Уэйда или правилами Уэйда–Мингоса [3] . Правила основаны на молекулярно-орбитальном подходе к связыванию [4] [5] [6] [7] Эти правила были расширены и унифицированы в форме правил Джеммиса [ 8] [9] .
Прогнозирование структур кластерных соединений
В зависимости от количества электронов на вершину применяются различные правила (4 n , 5 n или 6 n ).
Правила 4 n достаточно точны в предсказании структур кластеров, имеющих около 4 электронов на вершину, как в случае многих боранов и карборанов . Для таких кластеров структуры основаны на дельтаэдрах , которые являются многогранниками , в которых каждая грань треугольная. Кластеры 4 n классифицируются как клозо- , нидо- , арахно- или гифо- , в зависимости от того, представляют ли они полный ( клозо- ) дельтаэдр или дельтаэдр, в котором отсутствует одна ( нидо- ), две ( арахно- ) или три ( гифо- ) вершины.
Однако гифокластеры встречаются относительно редко из-за того, что число электронов достаточно велико, чтобы начать заполнять антисвязывающие орбитали и дестабилизировать структуру 4 n . Если число электронов близко к 5 электронам на вершину, структура часто меняется на структуру, регулируемую правилами 5n, которые основаны на 3-связанных многогранниках.
По мере дальнейшего увеличения числа электронов структуры кластеров с числом электронов 5n становятся нестабильными, поэтому могут быть реализованы правила 6 n . Кластеры 6 n имеют структуры, основанные на кольцах.
Молекулярно-орбитальный подход может быть использован для обоснования связей кластерных соединений типов 4 n , 5 n и 6 n .
4нправила
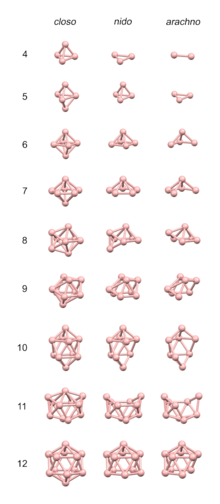
Следующие многогранники являются замкнутыми многогранниками и являются основой для правил 4 n ; каждый из них имеет треугольные грани. [10] Количество вершин в кластере определяет, на каком многограннике основана структура.
| Количество вершин | Многогранник |
|---|---|
| 4 | Тетраэдр |
| 5 | Тригональная бипирамида |
| 6 | Октаэдр |
| 7 | Пентагональная бипирамида |
| 8 | D 2d (треугольный) додекаэдр ( плосконосый двуклиноид ) |
| 9 | Трехшапочная тригональная призма |
| 10 | Молекулярная геометрия с двумя квадратными головками и антипризматической призмой |
| 11 | Икосаэдр со суженными ребрами (октадекаэдр) |
| 12 | Икосаэдр (двуглавая пятиугольная антипризма) |
Используя число электронов, можно найти предсказанную структуру. n — число вершин в кластере. 4 правила n перечислены в следующей таблице.
| Количество электронов | Имя | Предсказанная структура |
|---|---|---|
| 4 н − 2 | Двушапочный клозо | n − 2 вершинный замкнутый многогранник с 2 закрытыми ( дополненными ) гранями |
| 4 н | Закрыто | n − 1 вершинный замкнутый многогранник с 1 закрытой гранью |
| 4 н + 2 | близко | замкнутый многогранник с n вершинами |
| 4 н + 4 | нидо | n + 1 вершинный замкнутый многогранник с 1 отсутствующей вершиной |
| 4н + 6 | арахно | n + 2 вершинный замкнутый многогранник с 2 отсутствующими вершинами |
| 4н + 8 | гифо | n + 3 вершинный замкнутый многогранник с 3 отсутствующими вершинами |
| 4н + 10 | кладо | n + 4 вершинный замкнутый многогранник с 4 отсутствующими вершинами |
10
При подсчете электронов для каждого кластера подсчитывается число валентных электронов . Для каждого присутствующего переходного металла из общего числа электронов вычитается 10 электронов. Например, в Rh 6 (CO) 16 общее число электронов будет равно 6 × 9 + 16 × 2 − 6 × 10 = 86 – 60 = 26. Следовательно, кластер является замкнутым полиэдром, поскольку n = 6 , с 4 n + 2 = 26 .

4
При прогнозировании структуры кластеров можно учитывать и другие правила:
- Для кластеров, состоящих в основном из переходных металлов, любые присутствующие элементы основной группы часто лучше всего считать лигандами или междоузельными атомами, а не вершинами.
- Более крупные и электроположительные атомы имеют тенденцию занимать вершины с высокой степенью связности, а более мелкие и электроотрицательные атомы имеют тенденцию занимать вершины с низкой степенью связности.
- В особом случае кластеров гидрида бора каждый атом бора, связанный с 3 или более вершинами, имеет один конечный гидрид, в то время как атом бора, связанный с двумя другими вершинами, имеет два конечных атома водорода. Если присутствует больше атомов водорода, они размещаются в открытых гранях, чтобы выровнять координационное число вершин.
- В особом случае кластеров переходных металлов лиганды добавляются к металлическим центрам, чтобы придать металлам разумные координационные числа, а если присутствуют какие-либо атомы водорода , они помещаются в мостиковые положения, чтобы выровнять координационные числа вершин.
В общем случае замкнутые структуры с n вершинами представляют собой n- вершинные многогранники.
Для прогнозирования структуры нидо -кластера в качестве отправной точки используется клозо- кластер с n + 1 вершиной; если кластер состоит из мелких атомов, то удаляется вершина с высокой связностью, а если кластер состоит из крупных атомов, то удаляется вершина с низкой связностью.
Для прогнозирования структуры кластера арахно в качестве отправной точки используется замкнутый многогранник с n + 2 вершинами, а комплекс нидо с n + 1 вершиной генерируется в соответствии с правилом, указанным выше; вторая вершина, смежная с первой, удаляется, если кластер состоит в основном из мелких атомов, вторая вершина, не смежная с первой, удаляется, если кластер состоит в основном из крупных атомов.
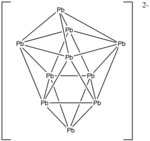
Пример: Pb2−
10
- Число электронов: 10 × Pb + 2 (для отрицательного заряда) = 10 × 4 + 2 = 42 электрона.
- Так как n = 10, то 4 n + 2 = 42, поэтому кластер представляет собой замкнутую двушапочную квадратную антипризму.
Пример: С2+
4
- Число электронов: 4 × S – 2 (для положительного заряда) = 4 × 6 – 2 = 22 электрона.
- Так как n = 4, то 4 n + 6 = 22, поэтому кластер является арахно .
- Начиная с октаэдра, удаляется вершина с высокой связностью, а затем удаляется несмежная вершина.
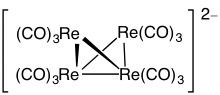
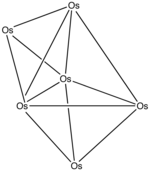
Пример: Os 6 (CO) 18
- Число электронов: 6 × Os + 18 × CO – 60 (для 6 атомов осмия) = 6 × 8 + 18 × 2 – 60 = 24
- Так как n = 6, 4 n = 24, то кластер ограничен близко .
- Начиная с тригональной бипирамиды, грань закрыта. Карбонилы были опущены для ясности.
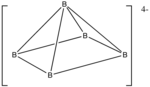
5ЧАС4−
5, атомы водорода опущены
Пример: [11] Б
5ЧАС4−
5
- Число электронов: 5 × B + 5 × H + 4 (для отрицательного заряда) = 5 × 3 + 5 × 1 + 4 = 24
- Так как n = 5, то 4 n + 4 = 24, поэтому кластер — нидо.
- Начиная с октаэдра, удаляется одна из вершин.
Правила полезны также для предсказания структуры карборанов . Пример: C 2 B 7 H 13
- Число электронов = 2 × C + 7 × B + 13 × H = 2 × 4 + 7 × 3 + 13 × 1 = 42
- Поскольку n в этом случае равно 9, 4 n + 6 = 42, кластер является арахно .
Бухгалтерия для дельтаэдрических кластеров иногда осуществляется путем подсчета скелетных электронов вместо общего числа электронов. Скелетные орбитали (электронная пара) и скелетные электроны для четырех типов дельтаэдрических кластеров следующие:
- n -вершинная замкнутая : n + 1 скелетные орбитали, 2 n + 2 скелетных электрона
- n -вершинное нидо : n + 2 скелетные орбитали, 2 n + 4 скелетных электрона
- n -вершинная арахно : n + 3 скелетных орбиталей, 2 n + 6 скелетных электронов
- n -вершинная гифо : n + 4 скелетных орбиталей, 2 n + 8 скелетных электронов
Количество скелетных электронов определяется путем суммирования следующего количества электронов:
- 2 от каждого подразделения BH
- 3 от каждого блока ЦХ
- 1 от каждого дополнительного атома водорода (сверх атомов в единицах BH и CH)
- анионные электроны заряда
5нправила
Как обсуждалось ранее, правило 4 n в основном касается кластеров с количеством электронов 4 n + k , в которых примерно 4 электрона находятся на каждой вершине. По мере добавления большего количества электронов на вершину число электронов на вершину приближается к 5. Вместо того чтобы принимать структуры, основанные на дельтаэдрах, кластеры типа 5n имеют структуры, основанные на другой серии многогранников, известных как 3-связанные многогранники , в которых каждая вершина соединена с 3 другими вершинами. 3-связанные многогранники являются двойственными дельтаэдрам. Ниже перечислены общие типы 3-связанных многогранников.

| Количество вершин | Тип 3-связного многогранника |
|---|---|
| 4 | Тетраэдр |
| 6 | Тригональная призма |
| 8 | Куб |
| 10 | Пятиугольная призма |
| 12 | D 2d псевдооктаэдр (двойник плосконосого двуклиноида) |
| 14 | Двойственная триаугментированная треугольная призма ( ассоциаэдр К 5 ) |
| 16 | Квадратный усеченный трапецоэдр |
| 18 | Двойственный икосаэдру с суженными ребрами |
| 20 | Додекаэдр |
Правила 5 n следующие.
| Общее количество электронов | Предсказанная структура |
|---|---|
| 5 н | n- вершинный 3-связный многогранник |
| 5 н + 1 | n – 1 вершинный 3-связный многогранник с одной вершиной, вставленной в ребро |
| 5 н + 2 | n – 2-вершинный 3-связный многогранник с двумя вершинами, вставленными в ребра |
| 5 н + к | n − k вершинный 3-связный многогранник с k вершинами, вставленными в ребра |
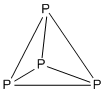
Пример: П 4
- Число электронов: 4 × P = 4 × 5 = 20
- Это структура 5 n с n = 4, поэтому она тетраэдрическая.
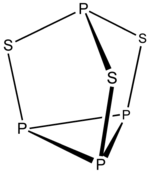
Пример: П 4 С 3
- Число электронов 4 × P + 3 × S = 4 × 5 + 3 × 6 = 38
- Это структура 5 n + 3, где n = 7. Три вершины вставлены в ребра
Пример: П 4 О 6
- Число электронов 4 × P + 6 × O = 4 × 5 + 6 × 6 = 56
- Это структура 5 n + 6, где n = 10. Шесть вершин вставлены в ребра
6нправила
По мере добавления большего количества электронов в кластер 5 n число электронов на вершину приближается к 6. Вместо принятия структур, основанных на правилах 4 n или 5 n , кластеры, как правило, имеют структуры, управляемые правилами 6 n , которые основаны на кольцах. Правила для структур 6 n следующие.
| Общее количество электронов | Предсказанная структура |
|---|---|
| 6 н – к | n -членное кольцо с k ⁄ 2 трансаннулярными связями |
| 6 н – 4 | n -членное кольцо с 2 трансаннулярными связями |
| 6 н – 2 | n -членное кольцо с 1 трансаннулярной связью |
| 6 н | n- членное кольцо |
| 6 н + 2 | n -членная цепь ( n- членное кольцо с 1 разорванной связью) |
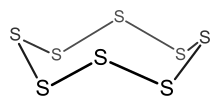
Пример: С 8
- Число электронов = 8 × S = 8 × 6 = 48 электронов.
- Так как n = 8, то 6 n = 48, поэтому кластер представляет собой 8-членное кольцо.

Гексан ( C6H14 )
- Число электронов = 6 × C + 14 × H = 6 × 4 + 14 × 1 = 38
- Так как n = 6, то 6 n = 36 и 6 n + 2 = 38, то кластер представляет собой 6-членную цепь.
Изолобальные вершинные единицы
При условии, что вершинная единица является изолобальной с BH, то она может, в принципе, по крайней мере, быть заменена единицей BH, даже если BH и CH не являются изоэлектронными. Единица CH + является изолобальной, поэтому правила применимы к карборанам. Это можно объяснить с помощью граничной орбитальной обработки. [10] Кроме того, существуют изолобальные единицы переходных металлов. Например, Fe(CO) 3 обеспечивает 2 электрона. Вывод этого кратко выглядит следующим образом:
- У железа 8 валентных электронов.
- Каждая карбонильная группа является чистым донором 2 электронов с учетом внутренних σ- и π-связей , что дает 14 электронов.
- Считается, что 3 пары участвуют в образовании σ-связи Fe–CO , а 3 пары участвуют в образовании π -связей от Fe к CO, что снижает число 14 до 2.
Связывание в кластерных соединениях
- близко - B
6ЧАС2−
6

6ЧАС2−
6показывая орбитали, ответственные за формирование кластера. Показаны графические представления орбиталей; наборы МО симметрии T и E будут иметь два или одно дополнительное графическое представление, соответственно, которые здесь не показаны.
- Атомы бора лежат на каждой вершине октаэдра и sp-гибридизованы. [11] Один sp-гибрид излучается от структуры, образуя связь с атомом водорода. Другой sp-гибрид излучается в центр структуры, образуя большую связывающую молекулярную орбиталь в центре кластера. Оставшиеся две негибридизованные орбитали лежат вдоль касательной к сфероподобной структуре, создавая больше связывающих и разрыхляющих орбиталей между вершинами бора. [9] Орбитальная диаграмма разбивается следующим образом:
- 18 каркасных молекулярных орбиталей (МО), полученных из 18 атомных орбиталей бора, следующие:
- 1 связывающая МО в центре кластера и 5 разрыхляющих МО из 6 sp-радиальных гибридных орбиталей
- 6 связывающих МО и 6 разрыхляющих МО из 12 тангенциальных p-орбиталей.
- 18 каркасных молекулярных орбиталей (МО), полученных из 18 атомных орбиталей бора, следующие:
- Таким образом, общее число скелетных связывающих орбиталей равно 7, т.е. n + 1 .
Кластеры переходных металлов
Кластеры переходных металлов используют d-орбитали для связывания . Таким образом, они имеют до девяти связывающих орбиталей, вместо только четырех, присутствующих в кластерах бора и основной группы. [12] [13] PSEPT также применим к металлаборанам
Кластеры с внедренными атомами
Благодаря своим большим радиусам переходные металлы обычно образуют кластеры, которые больше, чем основные элементы группы. Одним из следствий их увеличенного размера является то, что эти кластеры часто содержат атомы в своих центрах. Ярким примером является [Fe 6 C(CO) 16 ] 2- . В таких случаях правила подсчета электронов предполагают, что междоузельный атом вносит все валентные электроны в кластерную связь. Таким образом, [Fe 6 C(CO) 16 ] 2- эквивалентен [Fe 6 (CO) 16 ] 6- или [Fe 6 (CO) 18 ] 2- . [14]
Смотрите также
Ссылки
- ^ Уэйд, К. (1971). «Структурное значение числа скелетных связывающих электронных пар в карборанах, высших боранах и анионах борана, а также различных соединениях карбонильных кластеров переходных металлов». J. Chem. Soc. D . 1971 (15): 792– 793. doi :10.1039/C29710000792.
- ^ Мингос, ДМП (1972). «Общая теория кластерных и кольцевых соединений главной группы и переходных элементов». Nature Physical Science . 236 (68): 99– 102. Bibcode : 1972NPhS..236...99M. doi : 10.1038/physci236099a0.
- ^ Уэлч, Алан Дж. (2013). «Значение и влияние правил Уэйда». Chem. Commun . 49 (35): 3615– 3616. doi :10.1039/C3CC00069A. PMID 23535980.
- ^ Уэйд, К. (1976). «Структурные и связующие модели в кластерной химии». Adv. Inorg. Chem. Radiochem . Достижения в неорганической химии и радиохимии. 18 : 1– 66. doi :10.1016/S0065-2792(08)60027-8. ISBN 9780120236183.
- ^ Джиролами, Г. (осень 2008 г.). «Конспекты лекций, распространенные в Университете Иллинойса, Урбана-Шампейн».
{{cite journal}}: Цитировать журнал требует|journal=( помощь ) Эти заметки содержали оригинальный материал, который послужил основой для разделов по правилам 4 n , 5 n и 6 n . - ^ Gilespie, RJ (1979). «Лекции памяти Нихольма». Chem. Soc. Rev. 8 (3): 315–352 . doi :10.1039/CS9790800315.
- ^ Мингос, ДМП (1984). «Подход к многогранным скелетным электронным парам». Acc. Chem. Res. 17 (9): 311– 319. doi :10.1021/ar00105a003.
- ^ Джеммис, Элуватингал Д.; Балакришнараджан, Мусири М.; Панчаратна, Паттат Д. (2001). «Унифицированное правило подсчета электронов для макрополиэдрических боранов, металлоборанов и металлоценов». J. Am. Chem. Soc. 123 (18): 4313– 4323. doi :10.1021/ja003233z. PMID 11457198.
- ^ аб Джеммис, Элуватингал Д.; Балакришнараджан, Мусири М.; Панчаратна, Паттат Д. (2002). «Электронные требования к макрополиэдрическим боранам». хим. 102 (1): 93–144 . doi : 10.1021/cr990356x. ПМИД 11782130.
- ^ ab Коттон, Ф. Альберт ; Уилкинсон, Джеффри ; Мурильо, Карлос А.; Бохманн, Манфред (1999), Advanced Inorganic Chemistry (6-е изд.), Нью-Йорк: Wiley-Interscience, ISBN 0-471-19957-5
- ^ ab Коттон, Альберт (1990). Химические приложения теории групп . John Wiley & Sons. стр. 205–251. ISBN 0-471-51094-7.
- ^ Кинг, Р. Б.; Руврэ, Д. Х. (1977). «Химические приложения теории групп и топологии. 7. Теоретико-графовая интерпретация топологии связей в полиэдрических боранах, карборанах и металлических кластерах». J. Am. Chem. Soc. 99 (24): 7834– 7840. doi :10.1021/ja00466a014.
- ^ Костикова, ГП; Корольков, ДВ (1985). "Электронная структура кластерных комплексов переходных металлов со слабо- и сильнополевыми лигандами". Russ. Chem. Rev. 54 ( 4): 591– 619. Bibcode :1985RuCRv..54..344K. doi :10.1070/RC1985v054n04ABEH003040. S2CID 250797537.
- ^ Фельнер, Томас П. (2006). "Кластерные соединения: неорганометаллические соединения, содержащие переходные металлы и элементы главной группы". Энциклопедия неорганической химии . doi :10.1002/0470862106.ia097. ISBN 0470860782.
Общие ссылки
- Гринвуд, Норман Н.; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-08-037941-8.
- Коттон, Ф. Альберт ; Уилкинсон, Джеффри ; Мурильо, Карлос А.; Бохманн, Манфред (1999), Advanced Inorganic Chemistry (6-е изд.), Нью-Йорк: Wiley-Interscience, ISBN 0-471-19957-5