Расчет свойств стекла

Расчет свойств стекла ( моделирование стекла ) используется для прогнозирования интересующих свойств стекла или поведения стекла в определенных условиях (например, во время производства) без экспериментального исследования, на основе прошлых данных и опыта, с целью экономии времени, материальных, финансовых и экологических ресурсов или для получения научного понимания. Впервые он был применен в конце 19 века А. Винкельманном и О. Шоттом . Сочетание нескольких моделей стекла вместе с другими соответствующими функциями может использоваться для оптимизации и процедур шести сигм . В форме статистического анализа моделирование стекла может помочь с аккредитацией новых данных, экспериментальных процедур и измерительных учреждений (лабораторий стекла).

Исторически расчет свойств стекла напрямую связан с основанием науки о стекле . В конце 19 века физик Эрнст Аббе разработал уравнения, которые позволяют рассчитать конструкцию оптимизированных оптических микроскопов в Йене , Германия , стимулируемый сотрудничеством с оптической мастерской Карла Цейсса . До времени Эрнста Аббе создание микроскопов было в основном произведением искусства и опытным мастерством, что приводило к очень дорогим оптическим микроскопам с переменным качеством. Теперь Эрнст Аббе точно знал, как построить превосходный микроскоп, но, к сожалению, необходимых линз и призм с определенными соотношениями показателя преломления и дисперсии не существовало. Эрнст Аббе не смог найти ответы на свои потребности у художников и инженеров по стеклу; в то время производство стекла не основывалось на науке. ^[2]

В 1879 году молодой инженер-стеклодув Отто Шотт отправил Аббе образцы стекла со специальным составом ( литийсиликатное стекло), которое он приготовил сам и которое, как он надеялся, должно было продемонстрировать особые оптические свойства. После измерений Эрнста Аббе образцы стекла Шотта не обладали желаемыми свойствами, и они также не были настолько однородными, как хотелось бы. Тем не менее, Эрнст Аббе пригласил Отто Шотта поработать над этой проблемой дальше и систематически оценить все возможные компоненты стекла. Наконец, Шотту удалось получить однородные образцы стекла, и он изобрел боросиликатное стекло с оптическими свойствами, необходимыми Аббе. ^[2] Эти изобретения дали начало известным компаниям Zeiss и Schott Glass (см. также Хронология технологии микроскопии ). Зародилось систематическое исследование стекла. В 1908 году Юджин Салливан основал исследование стекла также в Соединенных Штатах ( Корнинг , Нью-Йорк ). ^[3]

В начале исследований стекла было наиболее важно знать связь между составом стекла и его свойствами. Для этой цели Отто Шотт ввел принцип аддитивности в нескольких публикациях для расчета свойств стекла. ^{[4] [5] [6]} Этот принцип подразумевает, что связь между составом стекла и определенным свойством является линейной для всех концентраций компонентов стекла, предполагая идеальную смесь , где C _i и b _i представляют собой определенные концентрации компонентов стекла и соответствующие коэффициенты соответственно в уравнении ниже. Принцип аддитивности является упрощением и действителен только в узких диапазонах состава, как видно на представленных диаграммах для показателя преломления и вязкости. Тем не менее, применение принципа аддитивности привело ко многим изобретениям Шотта, включая оптические стекла, стекла с низким тепловым расширением для кухонной и лабораторной посуды ( Duran ) и стекла с уменьшенным понижением точки замерзания для ртутных термометров . Впоследствии Инглиш ^[7] и Гельхофф и др. ^[8] опубликовали аналогичные модели расчета свойств аддитивного стекла. Принцип аддитивности Шотта до сих пор широко используется в исследованиях и технологиях стекла. ^{[9] [10]}

Принцип аддитивности:    ${\displaystyle {\mbox{Свойство стекла}}=b_{0}+\sum _{i=1}^{n}b_{i}C_{i}}$

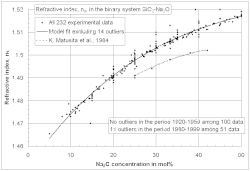
Шотт и многие ученые и инженеры впоследствии применили принцип аддитивности к экспериментальным данным, измеренным в их собственной лаборатории в достаточно узких диапазонах состава ( локальные модели стекла ). Это наиболее удобно, поскольку не нужно учитывать разногласия между лабораториями и нелинейные взаимодействия компонентов стекла. В течение нескольких десятилетий систематических исследований стекла были изучены тысячи составов стекла , что привело к миллионам опубликованных свойств стекла, собранных в базах данных стекла . Этот огромный пул экспериментальных данных не был исследован в целом, пока Боттинга, ^[13] Кучук, ^[14] Привен, ^[15] Чоудхари, ^[16] Мазурин, ^[17] и Флюгель ^{[18] [19]} не опубликовали свои глобальные модели стекла , используя различные подходы. В отличие от моделей Шотта, глобальные модели учитывают множество независимых источников данных, что делает оценки модели более надежными. Кроме того, глобальные модели могут выявлять и количественно определять неаддитивные влияния определенных комбинаций компонентов стекла на свойства, такие как эффект смешанной щелочи, как показано на соседней диаграмме, или аномалию бора . Глобальные модели также отражают интересные разработки в области точности измерения свойств стекла , например, снижение точности экспериментальных данных в современной научной литературе для некоторых свойств стекла, показанных на диаграмме. Их можно использовать для аккредитации новых данных, экспериментальных процедур и измерительных учреждений (лабораторий стекла). В следующих разделах (за исключением энтальпии плавления) представлены методы эмпирического моделирования, которые кажутся успешным способом обработки огромных объемов экспериментальных данных. Полученные модели применяются в современной инженерии и исследованиях для расчета свойств стекла.

Существуют неэмпирические ( дедуктивные ) модели стекла. ^[20] Они часто создаются не для получения надежных предсказаний свойств стекла в первую очередь (за исключением энтальпии плавления), а для установления связей между несколькими свойствами (например, атомным радиусом , атомной массой , прочностью и углами химической связи , химической валентностью , теплоемкостью ) для получения научного понимания. В будущем исследование связей свойств в дедуктивных моделях может в конечном итоге привести к надежным предсказаниям для всех желаемых свойств, при условии, что связи свойств хорошо поняты и все необходимые экспериментальные данные доступны.

Свойства стекла и поведение стекла в процессе производства можно рассчитать с помощью статистического анализа баз данных по стеклу, таких как GE-SYSTEM ^[21], SciGlass ^[22] и Interglad, ^[23], иногда в сочетании с методом конечных элементов . Для оценки энтальпии плавления используются термодинамические базы данных.

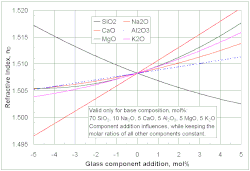
Если желаемое свойство стекла не связано с кристаллизацией (например, температура ликвидуса ) или разделением фаз , можно применить линейную регрессию с использованием общих полиномиальных функций до третьей степени. Ниже приведен пример уравнения второй степени. Значения C представляют собой концентрации компонентов стекла, таких как Na2O _или CaO в процентах или других долях, значения b представляют собой коэффициенты, а n представляет собой общее количество компонентов стекла. Основной компонент стекла кремний (SiO2 ₎ исключен из уравнения ниже из-за избыточной параметризации из-за ограничения, что все компоненты в сумме составляют 100%. Многие члены в уравнении ниже могут быть проигнорированы на основе корреляционного и значимого анализа. Систематические ошибки, такие как показано на рисунке, количественно определяются фиктивными переменными . Более подробная информация и примеры доступны в онлайн-руководстве Флюгеля. ^[24]

${\displaystyle {\mbox{Свойство стекла}}=b_{0}+\sum _{i=1}^{n}\left(b_{i}C_{i}+\sum _{k=i}^{n}b_{ik}C_{i}C_{k}\right)}$

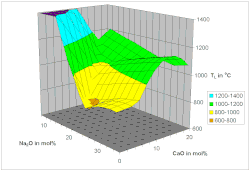
Температура ликвидуса была смоделирована с помощью нелинейной регрессии с использованием нейронных сетей ^[26] и несвязанных пиковых функций. ^[25] Подход несвязанных пиковых функций основан на наблюдении, что в пределах одной первичной кристаллической фазы может быть применена линейная регрессия поля ^[27] , а в эвтектических точках происходят резкие изменения.

Энтальпия плавления стекла отражает количество энергии, необходимое для преобразования смеси сырья ( партии ) в расплавленное стекло. Она зависит от состава парти и стекла, от эффективности печи и систем регенерации тепла, среднего времени пребывания стекла в печи и многих других факторов. Пионерская статья на эту тему была написана Карлом Крёгером в 1953 году. ^[28]

Для моделирования течения стекла в стекловаренной печи метод конечных элементов применяется в коммерческих целях ^{[29] [30]} на основе данных или моделей для вязкости , плотности , теплопроводности , теплоемкости , спектров поглощения и других соответствующих свойств расплава стекла. Метод конечных элементов может также применяться к процессам формования стекла.

Часто требуется оптимизировать несколько свойств стекла одновременно, включая производственные затраты. ^{[21] [31]} Это можно сделать, например, с помощью симплексного поиска или в электронной таблице следующим образом:

1. Перечень желаемых объектов недвижимости;
2. Ввод моделей для достоверного расчета свойств на основе состава стекла, включая формулу для оценки себестоимости продукции;
3. Расчет квадратов разностей (ошибок) между желаемыми и расчетными свойствами;
4. Сокращение суммы квадратичных ошибок с помощью опции Solver ^[32] в Microsoft Excel с компонентами стекла в качестве переменных. Другое программное обеспечение (например, Microcal Origin ) также может быть использовано для выполнения этих оптимизаций .

Можно по-разному взвешивать желаемые свойства. Основную информацию о принципе можно найти в статье Хаффа и др. ^[33]. Сочетание нескольких моделей стекла вместе с другими соответствующими технологическими и финансовыми функциями можно использовать в оптимизации методом шести сигм .

• Расчет партии стекла