Модель Кокса–Ингерсолла–Росса
Стохастическая модель эволюции финансовых процентных ставок
Три траектории процессов CIR

В математических финансах модель Кокса–Ингерсолла–Росса (CIR) описывает эволюцию процентных ставок . Это тип «однофакторной модели» ( модель краткосрочной ставки ), поскольку она описывает изменения процентных ставок как вызванные только одним источником рыночного риска . Модель может использоваться при оценке процентных деривативов . Она была введена в 1985 году [1] Джоном К. Коксом , Джонатаном Э. Ингерсоллом и Стивеном А. Россом как расширение модели Васичека , которая сама по себе является процессом Орнштейна–Уленбека .

Модель

Процесс CIR

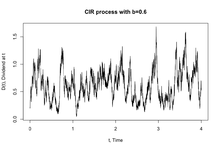
Модель CIR описывает мгновенную процентную ставку с помощью процесса квадратного корня Феллера , стохастическое дифференциальное уравнение которого имеет вид г т {\displaystyle r_{t}}

г г т = а ( б − г т ) г т + σ г т г Вт т , {\displaystyle dr_{t}=a(b-r_{t})\,dt+\sigma {\sqrt {r_{t}}}\,dW_{t},}

где — процесс Винера (моделирующий случайный рыночный фактор риска), а , , и — параметры . Параметр соответствует скорости корректировки к среднему значению , и волатильности. Фактор дрейфа , точно такой же, как в модели Васичека. Он обеспечивает возврат процентной ставки к среднему значению в долгосрочной перспективе , при этом скорость корректировки регулируется строго положительным параметром . Вт т {\displaystyle W_{т}} а {\displaystyle а} б {\displaystyle б} σ {\displaystyle \сигма \,} а {\displaystyle а} б {\displaystyle б} σ {\displaystyle \сигма \,} а ( б − г т ) {\displaystyle a(b-r_{t})} б {\displaystyle б} а {\displaystyle а}

Фактор стандартного отклонения , , исключает возможность отрицательных процентных ставок для всех положительных значений и . Нулевая процентная ставка также исключается, если выполняется условие σ г т {\displaystyle \sigma {\sqrt {r_{t}}}} а {\displaystyle а} б {\displaystyle б}

2 а б ≥ σ 2 {\displaystyle 2ab\geq \sigma ^{2}\,}

выполняется. В более общем смысле, когда скорость ( ) близка к нулю, стандартное отклонение ( ) также становится очень малым, что ослабляет влияние случайного шока на скорость. Следовательно, когда скорость приближается к нулю, ее эволюция становится подчиненной фактору дрейфа, который толкает скорость вверх (к равновесию ). г т {\displaystyle r_{t}} σ г т {\displaystyle \sigma {\sqrt {r_{t}}}}

В случае [2] процесс квадратного корня Феллера может быть получен из квадрата процесса Орнштейна–Уленбека . Он эргодичен и обладает стационарным распределением. Он используется в модели Хестона для моделирования стохастической волатильности. 4 а б = σ 2 {\displaystyle 4ab=\сигма ^{2}\,}

Распределение

  • Будущее распределение
Распределение будущих значений процесса CIR можно вычислить в замкнутой форме:
г т + Т = И 2 с , {\displaystyle r_{t+T}={\frac {Y}{2c}},}
где , а Y — нецентральное распределение хи-квадрат со степенями свободы и параметром нецентральности . Формально функция плотности вероятности имеет вид: с = 2 а ( 1 − е − а Т ) σ 2 {\displaystyle c={\frac {2a}{(1-e^{-aT})\sigma ^{2}}}} 4 а б σ 2 {\displaystyle {\frac {4ab}{\sigma ^{2}}}} 2 с г т е − а Т {\displaystyle 2cr_{t}e^{-aT}}
ф ( г т + Т ; г т , а , б , σ ) = с е − ты − в ( в ты ) д / 2 я д ( 2 ты в ) , {\displaystyle f(r_{t+T};r_{t},a,b,\sigma )=c\,e^{-uv}\left({\frac {v}{u}}\right)^{q/2}I_{q}(2{\sqrt {uv}}),}
где , , , а — модифицированная функция Бесселя первого рода порядка . д = 2 а б σ 2 − 1 {\displaystyle q={\frac {2ab}{\sigma ^{2}}}-1} ты = с г т е − а Т {\displaystyle u=cr_{t}e^{-aT}} в = с г т + Т {\displaystyle v=cr_{t+T}} я д ( 2 ты в ) {\displaystyle I_{q}(2{\sqrt {uv}})} д {\displaystyle д}
  • Асимптотическое распределение
Из-за возврата к среднему, по мере увеличения времени распределение будет приближаться к гамма-распределению с плотностью вероятности: г ∞ {\displaystyle r_{\infty}}
ф ( г ∞ ; а , б , σ ) = β α Г ( α ) г ∞ α − 1 е − β г ∞ , {\displaystyle f(r_{\infty};a,b,\sigma)={\frac {\beta ^{\alpha}}{\Gamma (\alpha)}}r_{\infty}^{\alpha -1}e^{-\beta r_{\infty}},}
где и . β = 2 а / σ 2 {\displaystyle \beta =2a/\sigma ^{2}} α = 2 а б / σ 2 {\displaystyle \альфа =2ab/\сигма ^{2}}
Вывод асимптотического распределения

Чтобы вывести асимптотическое распределение для модели CIR, мы должны использовать уравнение Фоккера-Планка : п ∞ {\displaystyle p_{\infty}}

∂ п ∂ т + ∂ ∂ г [ а ( б − г ) п ] = 1 2 σ 2 ∂ 2 ∂ г 2 ( г п ) {\displaystyle {\partial p \over {\partial t}}+{\partial \over {\partial r}}[a(br)p]={1 \over {2}}\sigma ^{2}{\partial ^{2} \over {\partial r^{2}}}(rp)}

Нас интересует частный случай, когда , что приводит к упрощенному уравнению: ∂ т п → 0 {\displaystyle \partial _{t}p\rightarrow 0}

а ( б − г ) п ∞ = 1 2 σ 2 ( п ∞ + г г п ∞ г г ) {\displaystyle a(br)p_{\infty}={1 \over {2}}\sigma ^{2}\left(p_{\infty}+r{dp_{\infty} \over {dr}}\right)}

Определение и перестановка членов приводит к уравнению: α = 2 а б / σ 2 {\displaystyle \альфа =2ab/\сигма ^{2}} β = 2 а / σ 2 {\displaystyle \beta =2a/\sigma ^{2}}

α − 1 г − β = г г г бревно ⁡ п ∞ {\displaystyle {\alpha -1 \over {r}}-\beta ={d \over {dr}}\log p_{\infty }}

Интеграция показывает нам, что:

п ∞ ∝ г α − 1 е − β г {\displaystyle p_{\infty }\propto r^{\alpha -1}e^{-\beta r}}

В диапазоне эта плотность описывает гамма-распределение. Следовательно, асимптотическое распределение модели CIR является гамма-распределением. п ∞ ∈ ( 0 , ∞ ] {\displaystyle p_ {\infty }\in (0,\infty ]}

Характеристики

  • Среднее возвращение ,
  • Уровень волатильности, зависящий от уровня ( ), σ г т {\displaystyle \sigma {\sqrt {r_{t}}}}
  • Для данного положительного значения процесс никогда не коснется нуля, если ; в противном случае он может иногда касаться нулевой точки, г 0 {\displaystyle r_{0}} 2 а б ≥ σ 2 {\displaystyle 2ab\geq \sigma ^{2}}
  • Э ⁡ [ г т ∣ г 0 ] = г 0 е − а т + б ( 1 − е − а т ) {\displaystyle \operatorname {E} [r_{t}\mid r_{0}]=r_{0}e^{-at}+b(1-e^{-at})} , поэтому долгосрочное среднее значение равно , б {\displaystyle б}
  • Вар ⁡ [ г т ∣ г 0 ] = г 0 σ 2 а ( е − а т − е − 2 а т ) + б σ 2 2 а ( 1 − е − а т ) 2 . {\displaystyle \operatorname {Var} [r_{t}\mid r_{0}]=r_{0}{\frac {\sigma ^{2}}{a}}(e^{-at}-e^{-2at})+{\frac {b\sigma ^{2}}{2a}}(1-e^{-at})^{2}.}

Калибровка

Непрерывное SDE можно дискретизировать следующим образом:
г т + Δ т − г т = а ( б − г т ) Δ т + σ г т Δ т ε т , {\displaystyle r_{t+\Delta t}-r_{t}=a(b-r_{t})\,\Delta t+\sigma \,{\sqrt {r_{t}\Delta t}}\varepsilon _{t},}
что эквивалентно
г т + Δ т − г т г т = а б Δ т г т − а г т Δ т + σ Δ т ε т , {\displaystyle {\frac {r_{t+\Delta t}-r_{t}}{{\sqrt {r}}_{t}}}={\frac {ab\Delta t}{{\sqrt {r}}_{t}}}-a{\sqrt {r}}_{t}\Delta t+\sigma \,{\sqrt {\Delta t}}\varepsilon _{t},}
предоставлено niid (0,1). Это уравнение можно использовать для линейной регрессии. ε т {\displaystyle \varepsilon _ {t}}

Моделирование

Стохастическое моделирование процесса CIR может быть достигнуто с использованием двух вариантов:

Ценообразование облигаций

При предположении отсутствия арбитража облигация может быть оценена с использованием этого процесса процентной ставки. Цена облигации экспоненциально аффинна по процентной ставке:

П ( т , Т ) = А ( т , Т ) е − Б ( т , Т ) г т {\displaystyle P(t,T)=A(t,T)e^{-B(t,T)r_{t}}\!}

где

А ( т , Т ) = ( 2 час е ( а + час ) ( Т − т ) / 2 2 час + ( а + час ) ( е час ( Т − т ) − 1 ) ) 2 а б / σ 2 {\displaystyle A(t,T)=\left({\frac {2he^{(a+h)(Tt)/2}}{2h+(a+h)(e^{h(Tt)}-1)}}\right)^{2ab/\sigma ^{2}}}
Б ( т , Т ) = 2 ( е час ( Т − т ) − 1 ) 2 час + ( а + час ) ( е час ( Т − т ) − 1 ) {\displaystyle B(t,T)={\frac {2(e^{h(T-t)}-1)}{2h+(a+h)(e^{h(T-t)}-1)}}}
h = a 2 + 2 σ 2 {\displaystyle h={\sqrt {a^{2}+2\sigma ^{2}}}}

Расширения

Модель CIR использует особый случай базовой аффинной диффузии скачков , которая все еще допускает выражение в замкнутой форме для цен облигаций. В модель можно ввести изменяющиеся во времени функции, заменяющие коэффициенты, чтобы сделать ее согласованной с заранее заданной временной структурой процентных ставок и, возможно, волатильности. Наиболее общий подход представлен в Maghsoodi (1996). [3] Более послушный подход представлен в Brigo и Mercurio (2001b) [4] , где к модели добавляется внешний зависящий от времени сдвиг для согласованности с входной временной структурой ставок.

Значительное расширение модели CIR на случай стохастического среднего и стохастической волатильности дано Линь Ченом (1996) и известно как модель Чена . Более недавнее расширение для обработки волатильности кластера, отрицательных процентных ставок и различных распределений — это так называемый «CIR #» Орландо, Мининни и Буфало (2018, [5] 2019, [6] [7] 2020, [8] 2021, [9] 2023 [10] ), а более простое расширение, фокусирующееся на отрицательных процентных ставках, было предложено Ди Франческо и Каммом (2021, [11] 2022 [12] ), которые называются моделями CIR- и CIR--.

Смотрите также

Ссылки

  1. ^ "Теория временной структуры процентных ставок - Эконометрическое общество". www.econometricsociety.org . Получено 14 октября 2023 г.
  2. ^ Юлия Мишура, Андрей Пилипенко и Антон Юрченко-Титаренко (10 января 2024 г.): Маломерный процесс Кокса-Ингерсолла-Росса, Стохастика, DOI: 10.1080/17442508.2023.2300291
  3. ^ Магсуди, Юсеф (январь 1996 г.). «Решение проблемы структуры расширенного срока и оценки опциона на облигации». Математические финансы . 6 (1): 89– 109. doi :10.1111/j.1467-9965.1996.tb00113.x. ISSN  0960-1627.
  4. ^ Бриго, Дамиано; Меркурио, Фабио (2001-07-01). «Расширение детерминированного сдвига аналитически поддающихся обработке и однородных по времени краткосрочных моделей». Финансы и стохастика . 5 (3): 369– 387. doi :10.1007/PL00013541. ISSN  0949-2984. S2CID  35316609.
  5. ^ Орландо, Джузеппе; Минини, Роза Мария; Буфало, Микеле (2018). «Новый подход к моделированию краткосрочных ставок CIR». Новые методы моделирования фиксированного дохода . Вклад в науку управления. Springer International Publishing. стр.  35–43 . doi :10.1007/978-3-319-95285-7_2. ISBN 978-3-319-95284-0.
  6. ^ Орландо, Джузеппе; Минини, Роза Мария; Буфало, Микеле (1 января 2019 г.). «Новый подход к прогнозированию рыночных процентных ставок с помощью модели CIR». Исследования по экономике и финансам . 37 (2): 267– 292. doi :10.1108/SEF-03-2019-0116. ISSN  1086-7376. S2CID  204424299.
  7. ^ Орландо, Джузеппе; Мининни, Роза Мария; Буфало, Микеле (19 августа 2019 г.). «Калибровка процентных ставок с помощью модели CIR». Журнал Risk Finance . 20 (4): 370–387 . doi :10.1108/JRF-05-2019-0080. ISSN  1526-5943. S2CID  204435499.
  8. ^ Орландо, Джузеппе; Мининни, Роза Мария; Буфало, Микеле (июль 2020 г.). «Прогнозирование процентных ставок с помощью моделей Васичека и CIR: подход к разделению». Journal of Forecasting . 39 (4): 569– 579. arXiv : 1901.02246 . doi :10.1002/for.2642. ISSN  0277-6693. S2CID  126507446.
  9. ^ Орландо, Джузеппе; Буфало, Микеле (26.05.2021). «Прогнозирование процентных ставок: между Халлом и Уайтом и CIR# — как заставить работать однофакторную модель». Журнал прогнозирования . 40 (8): 1566–1580 . doi : 10.1002/for.2783 . ISSN  0277-6693.
  10. ^ Орландо, Джузеппе; Буфало, Микеле (14 июля 2023 г.). «Прогнозирование временных рядов с использованием модели CIR#: от беспокойных настроений на рынках до регулярного сезонного туризма». Технологическое и экономическое развитие экономики . 29 (4): 1216– 1238. doi : 10.3846/tede.2023.19294 . ISSN  2029-4921.
  11. ^ Ди Франческо, Марко; Камм, Кевин (4 октября 2021 г.). «Как обращаться с отрицательными процентными ставками в рамках CIR». SeMa Journal . 79 (4): 593– 618. arXiv : 2106.03716 . doi : 10.1007/s40324-021-00267-w . S2CID  235358123.
  12. ^ Ди Франческо, Марко; Камм, Кевин (2022). «О модели расширенного CIR с детерминированным сдвигом в рамках отрицательной процентной ставки». Международный журнал финансовых исследований . 10 (2): 38. doi : 10.3390/ijfs10020038 . hdl : 11585/916048 .

Дополнительные ссылки

  • Халл, Джон К. (2003). Опционы, фьючерсы и другие производные инструменты . Верхняя Сэддл-Ривер, Нью-Джерси: Prentice Hall . ISBN 0-13-009056-5.
  • Кокс, Дж. К .; Ингерсолл, Дж. Э .; Росс, С. А. (1985). «Теория временной структуры процентных ставок». Econometrica . 53 (2): 385–407 . doi :10.2307/1911242. JSTOR  1911242.
  • Магсуди, Й. (1996). «Решение расширенной временной структуры CIR и оценка опционов на облигации». Математические финансы . 6 (6): 89– 109. doi :10.1111/j.1467-9965.1996.tb00113.x.
  • Дамиано Бриго; Фабио Меркурио (2001). Модели процентных ставок — теория и практика с улыбкой, инфляцией и кредитом (2-е изд. 2006 г.). Springer Verlag. ISBN 978-3-540-22149-4.
  • Бриго, Дамиано; Фабио Меркурио (2001b). «Расширение детерминированного сдвига аналитически поддающихся обработке и однородных во времени моделей краткосрочных ставок». Финансы и стохастика . 5 (3): 369– 388. doi :10.1007/PL00013541. S2CID  35316609.
  • Библиотека с открытым исходным кодом, реализующая процесс CIR на Python
  • Орландо, Джузеппе; Мининни, Роза Мария; Буфало, Микеле (2020). «Прогнозирование процентных ставок с помощью моделей Васичека и CIR: подход с разделением». Журнал прогнозирования . 39 (4): 569– 579. arXiv : 1901.02246 . doi : 10.1002/for.2642. ISSN  1099-131X. S2CID  126507446.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Cox–Ingersoll–Ross_model&oldid=1256493509"