Внимание (машинное обучение)
Метод машинного обучения
Часть серии статей о
Машинное обучение
и интеллектуальный анализ данных
Парадигмы
Проблемы
Clustering
Dimensionality reduction
Structured prediction
Anomaly detection
Artificial neural network
Reinforcement learning
Learning with humans
Model diagnostics
Mathematical foundations
Journals and conferences
Related articles
Механизм внимания, обзор

Внимание — это метод машинного обучения , который определяет относительную важность каждого компонента в последовательности по отношению к другим компонентам в этой последовательности. В обработке естественного языка важность представлена ​​«мягкими» весами, назначенными каждому слову в предложении. В более общем смысле внимание кодирует векторы, называемые вложениями токенов , в последовательности фиксированной ширины , размер которых может варьироваться от десятков до миллионов токенов.

В отличие от «жестких» весов, которые вычисляются во время обратного прохода обучения, «мягкие» веса существуют только в прямом проходе и, следовательно, изменяются с каждым шагом ввода. Более ранние разработки реализовали механизм внимания в системе перевода языка последовательной рекуррентной нейронной сети (RNN), но более поздняя разработка, а именно трансформатор , удалила более медленную последовательную RNN и в большей степени полагалась на более быструю параллельную схему внимания.

Вдохновленный идеями о внимании у людей , механизм внимания был разработан для устранения недостатков использования информации из скрытых слоев рекуррентных нейронных сетей. Рекуррентные нейронные сети отдают предпочтение более новой информации, содержащейся в словах в конце предложения, в то время как информация, находящаяся ранее в предложении, имеет тенденцию ослабляться . Внимание позволяет токену равный доступ к любой части предложения напрямую, а не только через предыдущее состояние.

История

Научные обзоры истории механизма внимания представлены в работах Ниу и др. [1] и Сойданера [2] .

Предшественники

Избирательное внимание у людей хорошо изучено в нейронауке и когнитивной психологии. [3] В 1953 году Колин Черри изучал избирательное внимание в контексте аудирования, известное как эффект коктейльной вечеринки . [4]

В 1958 году Дональд Бродбент предложил модель фильтра внимания . [5] Избирательное внимание зрения изучалось в 1960-х годах Джорджем Сперлингом в рамках парадигмы частичного отчета . Было также замечено, что контроль саккад модулируется когнитивными процессами, поскольку глаз преимущественно движется к областям высокой заметности . Поскольку ямка глаза мала, глаз не может резко разрешить все поле зрения сразу. Использование контроля саккад позволяет глазу быстро сканировать важные особенности сцены. [6]

Эти исследовательские разработки вдохновили такие алгоритмы, как Неокогнитрон и его варианты. [7] [8] Между тем, разработки в области нейронных сетей вдохновили модели схем биологического зрительного внимания. [9] [2] Например, одна хорошо цитируемая сеть 1998 года была вдохновлена ​​низкоуровневой зрительной системой приматов . Она создавала карты заметности изображений, используя созданные вручную (не выученные) признаки, которые затем использовались для руководства второй нейронной сетью при обработке участков изображения в порядке уменьшения заметности. [10]

Ключевой аспект механизма внимания можно записать (схематически) как: где угловые скобки обозначают скалярное произведение. Это показывает, что оно включает в себя мультипликативную операцию. Мультипликативные операции в искусственных нейронных сетях изучались под названиями группового метода обработки данных (1965) [11] [12] (где полиномы Колмогорова-Габора реализуют мультипликативные единицы или «ворота» [13] ), нейронные сети более высокого порядка , [14] единицы умножения , [15] единицы сигма-пи , [16] быстрые контроллеры веса , [17] и гиперсети . [18] ∑ i ⟨ ( query ) i , ( key ) i ⟩ ( value ) i {\displaystyle \sum _{i}\langle ({\text{query}})_{i},({\text{key}})_{i}\rangle ({\text{value}})_{i}}

В быстром контроллере веса ( Schmidhuber , 1992) одна из двух его сетей имеет «быстрые веса» или «динамические связи» (1981). [19] [20] [21] Медленная нейронная сеть обучается с помощью градиентного спуска для генерации ключей и значений для вычисления изменений веса быстрой нейронной сети, которая вычисляет ответы на запросы. [17] Позже было показано, что это эквивалентно ненормализованному линейному трансформатору. [22] В последующей статье была разработана похожая система с активным изменением веса. [23]

Повторяющееся внимание

В эпоху глубокого обучения был разработан механизм внимания для решения аналогичных проблем кодирования-декодирования. [1]

В машинном переводе модель seq2seq , предложенная в 2014 году [24], будет кодировать входной текст в вектор фиксированной длины, который затем будет декодироваться в выходной текст. Если входной текст длинный, вектор фиксированной длины не сможет нести достаточно информации для точного декодирования. Для решения этой проблемы был предложен механизм внимания.

В 2015 году была предложена модель подписи изображений, вдохновленная моделью seq2seq [25] , которая кодировала бы входное изображение в вектор фиксированной длины. Сюй и др. (2015), [26] ссылаясь на Бахданау и др. (2014), [27] применили механизм внимания, используемый в модели seq2seq, к подписи изображений.

Трансформатор

Одной из проблем с моделями seq2seq было использование ими рекуррентных нейронных сетей, которые не поддаются распараллеливанию, поскольку и кодер, и декодер должны обрабатывать последовательность токенов по одному токену. Decomposable Attention [28] попытались решить эту проблему, обрабатывая входную последовательность параллельно, перед вычислением «мягкой матрицы выравнивания» ( термин выравнивания используют Баганау и др. [27] ), чтобы обеспечить параллельную обработку.

Идея использования механизма внимания для собственного внимания вместо кодера-декодера (перекрестное внимание) также была предложена в этот период, например, в дифференцируемых нейронных компьютерах [29] и нейронных машинах Тьюринга . [30] Это было названо интра-вниманием [31], где LSTM дополняется сетью памяти, поскольку она кодирует входную последовательность.

Эти направления развития были объединены в 2017 году в архитектуре Transformer , опубликованной в статье Attention Is All You Need .

Обзор

Сеть внимания была разработана для выявления моделей высокой корреляции между словами в заданном предложении, предполагая, что она изучила модели корреляции слов из обучающих данных. Эта корреляция фиксируется как нейронные веса, изученные во время обучения с обратным распространением .

На диаграмме показана функция Attention forward pass, вычисляющая корреляции слова «that» с другими словами в «See that girl run». При наличии правильных весов от обучения сеть должна быть способна идентифицировать «girl» как высококоррелированное слово. Некоторые моменты, на которые следует обратить внимание:
  • Этот пример фокусируется на внимании одного слова "that". На практике внимание каждого слова вычисляется параллельно для ускорения вычислений. Простое изменение вектора "x" в нижнем регистре на матрицу "X" в верхнем регистре даст формулу для этого.
  • Масштабирование softmax qW k T / √ 100 предотвращает высокую дисперсию в qW k T , которая позволила бы одному слову чрезмерно доминировать над softmax, в результате чего внимание уделялось бы только одному слову, как это было бы при дискретном жестком max.
  • Нотация : обычно записанная выше формула softmax по строкам предполагает, что векторы являются строками, что противоречит стандартной математической нотации векторов столбцов. Правильнее было бы взять транспонирование вектора контекста и использовать softmax по столбцам , что привело бы к более правильной форме
( X W v ) T ∗ [ ( W k X T ) ∗ ( x _ W q ) T ] s m {\displaystyle {\begin{aligned}(XW_{v})^{T}*{[(W_{k}X^{T})*{({\underline {x}}W_{q})^{T}}]_{sm}}\end{aligned}}} .

Эта схема внимания была сравнена с аналогией Query-Key реляционных баз данных. Это сравнение предполагает асимметричную роль для векторов Query и Key, где один интересующий элемент (вектор Query «that») сопоставляется со всеми возможными элементами (векторами Key каждого слова в предложении). Однако параллельные вычисления как Self, так и Cross Attentions сопоставляют все токены матрицы K со всеми токенами матрицы Q; поэтому роли этих векторов симметричны . Возможно, потому что упрощенная аналогия с базой данных несовершенна, много усилий было вложено в дальнейшее понимание Attention путем изучения их ролей в целевых настройках, таких как контекстное обучение, [32] маскированные языковые задачи, [33] урезанные трансформаторы, [34] статистика биграмм, [35] статистика N-грамм, [36] попарные свертки, [37] и арифметическая факторизация. [38]

Машинный перевод

Сравнение потока данных в CNN, RNN и внутреннем внимании

Метод seq2seq, разработанный в начале 2010-х годов, использует две нейронные сети: сеть кодировщика преобразует входное предложение в числовые векторы, а сеть декодера преобразует эти векторы в предложения на целевом языке. Механизм Attention был привит к этой структуре в 2014 году и показан ниже. Позже он был усовершенствован в дизайне Transformer (2017).

Пошаговая последовательность языкового перевода
Кодер-декодер с вниманием.[39] Числовые индексы (100, 300, 500, 9k, 10k) указывают размеры векторов, а буквенные индексы i и i − 1 указывают временные шаги. Розоватые области в матрице H и векторе w — нулевые значения. Подробности см. в легенде.
Кодер-декодер с вниманием. [39] Числовые индексы (100, 300, 500, 9k, 10k) указывают размеры векторов, а буквенные индексы i и i − 1 указывают временные шаги. Розоватые области в матрице H и векторе w — нулевые значения. Подробности см. в легенде.
Легенда
ЭтикеткаОписание
100Макс. длина предложения
300Размер вложения (размер слова)
500Длина скрытого вектора
9к, 10кРазмер словаря входного и выходного языков соответственно.
х , Y9k и 10k 1-hot векторов словаря. x → x реализовано как таблица поиска, а не как векторное умножение. Y — это 1-hot максимизатор линейного слоя декодера D; то есть он берет argmax выходного сигнала линейного слоя D.
хВектор встраивания слов длиной 300. Векторы обычно предварительно рассчитываются из других проектов, таких как GloVe или Word2Vec .
часСкрытый вектор кодировщика длиной 500. В каждый момент времени этот вектор суммирует все предшествующие ему слова. Последний h можно рассматривать как вектор «предложения» или вектор мысли , как называет его Хинтон.
сВектор скрытого состояния декодера длиной 500.
Э500 нейронов рекуррентного нейросетевого кодера. 500 выходов. Количество входов составляет 800–300 от исходного внедрения + 500 от рекуррентных соединений. Кодер напрямую подает данные в декодер только для его инициализации, но не после этого; поэтому эта прямая связь показана очень слабо.
Д2-слойный декодер. Рекуррентный слой имеет 500 нейронов, а полностью связанный линейный слой имеет 10 тыс. нейронов (размер целевого словаря). [40] Только линейный слой имеет 5 миллионов (500 × 10 тыс.) весов – примерно в 10 раз больше весов, чем рекуррентный слой.
счет100-долгое выравнивание оценка
ж100-длинный векторный вес внимания. Это «мягкие» веса, которые изменяются во время прямого прохода, в отличие от «жестких» нейронных весов, которые изменяются во время фазы обучения.
АМодуль внимания – это может быть скалярное произведение рекуррентных состояний или полностью связанных слоев запрос-ключ-значение. Выход – вектор w длиной 100.
ЧАС500×100. 100 скрытых векторов h, объединенных в матрицу
сВектор контекста длиной 500 = H * w. c — линейная комбинация векторов h, взвешенных по w.

Интерпретация весов внимания

При переводе между языками выравнивание — это процесс сопоставления слов из исходного предложения со словами переведенного предложения. В примере I love you выше второе слово love выравнивается с третьим словом aime . Складывание мягких векторов строк вместе для je , t' и aime дает матрицу выравнивания :

ялюбовьты
je0,940,020,04
т'0.110,010,88
цель0,030,950,02

Иногда выравнивание может быть множественным-к-множеству. Например, английская фраза look it up соответствует cherchez-le . Таким образом, «мягкие» веса внимания работают лучше, чем «жесткие» веса внимания (устанавливая один вес внимания на 1, а другие на 0), поскольку мы хотели бы, чтобы модель создавала контекстный вектор, состоящий из взвешенной суммы скрытых векторов, а не «наилучший», поскольку наилучшего скрытого вектора может и не быть.

Этот взгляд на вес внимания решает часть проблемы объяснимости нейронной сети . Сети, которые выполняют дословный перевод без учета порядка слов, покажут самые высокие оценки вдоль (доминирующей) диагонали матрицы. Недиагональное доминирование показывает, что механизм внимания более нюансирован. При первом проходе через декодер 94% веса внимания приходится на первое английское слово I , поэтому сеть предлагает слово je . При втором проходе декодера 88% веса внимания приходится на третье английское слово you , поэтому она предлагает t' . При последнем проходе 95% веса внимания приходится на второе английское слово love , поэтому она предлагает aime .

seq2seq

Постановка проблемы

Анимация seq2seq с RNN и механизмом внимания

Рассмотрим задачу перевода с английского на французский язык языка seq2seq. Для конкретности рассмотрим перевод "the zone of international control <end>", который должен переводиться как "la zone de contrôle international <end>". Здесь мы используем специальный токен <end> в качестве управляющего символа для обозначения конца ввода как для кодера, так и для декодера.

Входная последовательность текста обрабатывается нейронной сетью (которая может быть LSTM, кодировщиком Transformer или какой-либо другой сетью) в последовательность векторов действительных значений , где обозначает «скрытый вектор». x 0 , x 1 , … {\displaystyle x_{0},x_{1},\dots } h 0 , h 1 , … {\displaystyle h_{0},h_{1},\dots } h {\displaystyle h}

После того, как кодер закончил обработку, декодер начинает работать над скрытыми векторами, чтобы создать выходную последовательность , авторегрессивно. То есть, он всегда принимает в качестве входных данных как скрытые векторы, созданные кодером, так и то, что сам декодер создал ранее, чтобы создать следующее выходное слово: y 0 , y 1 , … {\displaystyle y_{0},y_{1},\dots }

  1. ( , "<старт>") → "ла" h 0 , h 1 , … {\displaystyle h_{0},h_{1},\dots }
  2. ( , "<start> la") → "la Zone" h 0 , h 1 , … {\displaystyle h_{0},h_{1},\dots }
  3. ( , "<start> зона") → "зона де" h 0 , h 1 , … {\displaystyle h_{0},h_{1},\dots }
  4. ...
  5. ( , "<start> международная зона контроля") → "международная зона контроля <конец>" h 0 , h 1 , … {\displaystyle h_{0},h_{1},\dots }

Здесь мы используем специальный токен <start> в качестве управляющего символа для разграничения начала ввода для декодера. Декодирование завершается, как только в выводе декодера появляется "<end>".

Вес внимания

Механизм внимания с весами внимания, обзор.

Поскольку ручное создание весов противоречит цели машинного обучения, модель должна вычислять веса внимания самостоятельно. Используя аналогию с языком запросов к базе данных , мы заставляем модель конструировать тройку векторов: ключ, запрос и значение. Грубая идея заключается в том, что у нас есть «база данных» в форме списка пар ключ-значение. Декодер отправляет запрос и получает ответ в форме взвешенной суммы значений , где вес пропорционален тому, насколько близко запрос напоминает каждый ключ .

Декодер сначала частично обрабатывает входные данные "<start>", чтобы получить промежуточный вектор , 0-й скрытый вектор декодера. Затем промежуточный вектор преобразуется линейной картой в вектор запроса. Тем временем скрытые векторы, выводимые кодером, преобразуются другой линейной картой в ключевые векторы . Линейные карты полезны для предоставления модели достаточной свободы для поиска наилучшего способа представления данных. h 0 d {\displaystyle h_{0}^{d}} W Q {\displaystyle W^{Q}} q 0 = h 0 d W Q {\displaystyle q_{0}=h_{0}^{d}W^{Q}} W K {\displaystyle W^{K}} k 0 = h 0 W K , k 1 = h 1 W K , … {\displaystyle k_{0}=h_{0}W^{K},k_{1}=h_{1}W^{K},\dots }

Теперь запрос и ключи сравниваются с помощью скалярных произведений: . В идеале модель должна была научиться вычислять ключи и значения, так что is большой, is маленький, а остальные очень маленькие. Это можно интерпретировать так, что вес внимания должен быть в основном применен к 0-му скрытому вектору кодировщика, немного к 1-му и по сути ничего к остальным. q 0 k 0 T , q 0 k 1 T , … {\displaystyle q_{0}k_{0}^{T},q_{0}k_{1}^{T},\dots } q 0 k 0 T {\displaystyle q_{0}k_{0}^{T}} q 0 k 1 T {\displaystyle q_{0}k_{1}^{T}}

Чтобы сделать правильно взвешенную сумму, нам нужно преобразовать этот список скалярных произведений в распределение вероятностей по . Это можно сделать с помощью функции softmax , что даст нам веса внимания: Затем это используется для вычисления вектора контекста : 0 , 1 , … {\displaystyle 0,1,\dots } ( w 00 , w 01 , … ) = s o f t m a x ( q 0 k 0 T , q 0 k 1 T , … ) {\displaystyle (w_{00},w_{01},\dots )=\mathrm {softmax} (q_{0}k_{0}^{T},q_{0}k_{1}^{T},\dots )} c 0 = w 00 v 0 + w 01 v 1 + ⋯ {\displaystyle c_{0}=w_{00}v_{0}+w_{01}v_{1}+\cdots }

где — векторы значений , линейно преобразованные другой матрицей, чтобы предоставить модели свободу в поиске наилучшего способа представления значений. Без матриц модель была бы вынуждена использовать один и тот же скрытый вектор как для ключа, так и для значения, что может быть нецелесообразно, поскольку эти две задачи не одинаковы. v 0 = h 0 W V , v 1 = h 1 W V , … {\displaystyle v_{0}=h_{0}W^{V},v_{1}=h_{1}W^{V},\dots } W Q , W K , W V {\displaystyle W^{Q},W^{K},W^{V}}

Вычисление весов внимания с помощью скалярного произведения. Это «перекрестное внимание декодера».

Это механизм dot-attention. Конкретная версия, описанная в этом разделе, — это «перекрестное внимание декодера», поскольку выходной контекстный вектор используется декодером, а входные ключи и значения поступают от кодера, но запрос поступает от декодера, таким образом, «перекрестное внимание».

Более кратко, мы можем записать это как , где матрица — это матрица, строки которой . Обратите внимание, что вектор запроса, , не обязательно совпадает с вектором ключ-значение . Фактически, теоретически возможно, что векторы запроса, ключа и значения будут разными, хотя на практике это делается редко. c 0 = A t t e n t i o n ( h 0 d W Q , H W K , H W V ) = s o f t m a x ( ( h 0 d W Q ) ( H W K ) T ) ( H W V ) {\displaystyle c_{0}=\mathrm {Attention} (h_{0}^{d}W^{Q},HW^{K},HW^{V})=\mathrm {softmax} ((h_{0}^{d}W^{Q})\;(HW^{K})^{T})(HW^{V})} H {\displaystyle H} h 0 , h 1 , … {\displaystyle h_{0},h_{1},\dots } h 0 d {\displaystyle h_{0}^{d}} h 0 {\displaystyle h_{0}}

Варианты

Многие варианты внимания реализуют мягкие веса, такие как

  • быстрые весовые программисты или быстрые весовые контроллеры (1992). [17] «Медленная» нейронная сеть выводит «быстрые» веса другой нейронной сети через внешние продукты . Медленная сеть обучается методом градиентного спуска. Позднее она была переименована в «линеаризованное самовнимание». [22]
  • Внимание в стиле Баганау [41] , также называемое аддитивным вниманием ,
  • Внимание в стиле Луонга [42] , известное как мультипликативное внимание ,
  • высокопараллелизуемое внутреннее внимание, представленное в 2016 году как разложимое внимание [31] и успешно использованное в трансформаторах годом позже,
  • позиционное внимание и факторизованное позиционное внимание . [43]

Для сверточных нейронных сетей механизмы внимания можно различать по измерению, на котором они работают, а именно: пространственное внимание, [44] канальное внимание, [45] или их комбинации. [46] [47]

Много усилий было вложено в дальнейшее понимание внимания путем изучения его роли в целевых условиях, таких как контекстное обучение, [32] маскированные языковые задачи, [33] упрощенные трансформаторы, [34] статистика биграмм, [35] статистика N-грамм, [36] парные свертки, [37] и арифметическая факторизация. [38]

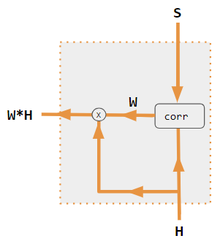
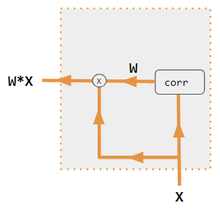
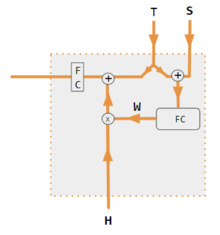
Эти варианты рекомбинируют входы на стороне кодировщика, чтобы перераспределить эти эффекты на каждый целевой выход. Часто корреляционная матрица скалярных произведений предоставляет коэффициенты повторного взвешивания. На рисунках ниже W — это матрица весов контекстного внимания, аналогичная формуле в разделе «Основные вычисления» выше.

1. скалярное произведение кодера-декодера2. кодер-декодер QKV3. скалярное произведение только для кодировщика4. QKV только для кодера5. Учебник Pytorch
Для вычисления внимания необходимы как кодер, так и декодер. [42]
Для вычисления внимания необходимы как кодер, так и декодер. [48]
Декодер не используется для вычисления внимания. При наличии только одного входа в corr, W является автокорреляцией скалярных произведений. w ij = x i x j . [49]
Декодер не используется для расчета внимания. [50]
Для вычисления внимания вместо корреляции скалярного произведения используется полностью связанный слой. [51]
Легенда
ЭтикеткаОписание
Переменные X, H, S, TПеременные верхнего регистра представляют все предложение, а не только текущее слово. Например, H — это матрица скрытого состояния кодировщика — одно слово на столбец.
С, ТS, скрытое состояние декодера; T, встраивание целевого слова. В варианте обучения Pytorch Tutorial T чередуется между 2 источниками в зависимости от уровня используемого принуждения учителя . T может быть встраиванием выходного слова сети; т. е. встраиванием(argmax(FC output)). В качестве альтернативы принуждению учителя T может быть встраиванием известного правильного слова, которое может произойти с постоянной вероятностью принуждения, скажем, 1/2.
Х, НH — скрытое состояние кодера; X — вложения входных слов.
ВтКоэффициенты внимания
Qw, Kw, Vw, FCМатрицы весов для запроса, ключа, значения соответственно. FC — полносвязная матрица весов.
⊕, ⊗⊕, конкатенация векторов; ⊗, умножение матриц.
коррСтолбцовый softmax(матрица всех комбинаций скалярных произведений). Скалярные произведения — x i * x j в варианте № 3, h i * s j в варианте 1 и столбец  i ( Kw * H ) * столбец  j ( Qw * S ) в варианте 2 и столбец  i ( Kw * X ) * столбец  j ( Qw * X ) в варианте 4. Вариант 5 использует полносвязный слой для определения коэффициентов. Если вариант — QKV, то скалярные произведения нормализуются с помощью √ d, где d — высота матриц QKV.

Само-внимание

Самовосприятие кодера, структурная схема
Самовосприятие кодера, подробная схема

Внимательность по сути то же самое, что и перекрестное внимание, за исключением того, что векторы запроса, ключа и значения исходят из одной и той же модели. И кодер, и декодер могут использовать внимание, но с тонкими различиями.

Для самовнимания кодировщика мы можем начать с простого кодировщика без самовнимания, например, «встроенного слоя», который просто преобразует каждое входное слово в вектор с помощью фиксированной таблицы поиска . Это дает последовательность скрытых векторов . Затем их можно применить к механизму внимания скалярного произведения, чтобы получить или, более кратко, . Это можно применять многократно, чтобы получить многослойный кодировщик. Это «самовнимание кодировщика», иногда называемое «вниманием всех ко всем», поскольку вектор в каждой позиции может уделять внимание каждому другому. h 0 , h 1 , … {\displaystyle h_{0},h_{1},\dots } h 0 ′ = A t t e n t i o n ( h 0 W Q , H W K , H W V ) h 1 ′ = A t t e n t i o n ( h 1 W Q , H W K , H W V ) ⋯ {\displaystyle {\begin{aligned}h_{0}'&=\mathrm {Attention} (h_{0}W^{Q},HW^{K},HW^{V})\\h_{1}'&=\mathrm {Attention} (h_{1}W^{Q},HW^{K},HW^{V})\\&\cdots \end{aligned}}} H ′ = A t t e n t i o n ( H W Q , H W K , H W V ) {\displaystyle H'=\mathrm {Attention} (HW^{Q},HW^{K},HW^{V})}

Маскировка

Декодер внутреннего внимания с причинной маскировкой, подробная схема

Для самовнимания декодера, все-ко-всем внимание не подходит, потому что во время процесса авторегрессивного декодирования декодер не может уделять внимание будущим выводам, которые еще не декодированы. Это можно решить, принудительно установив веса внимания для всех , что называется «каузальной маскировкой». Этот механизм внимания — «каузально замаскированное самовнимание». w i j = 0 {\displaystyle w_{ij}=0} i < j {\displaystyle i<j}

Оптимизации

Вспышка внимания

Размер матрицы внимания пропорционален квадрату числа входных токенов. Поэтому, когда вход длинный, вычисление матрицы внимания требует большого объема памяти GPU . Flash Atmeast — это реализация, которая снижает потребность в памяти и повышает эффективность без ущерба для точности. Это достигается путем разбиения вычисления внимания на более мелкие блоки, которые помещаются в более быструю память на чипе GPU, что снижает необходимость хранить большие промежуточные матрицы и, таким образом, снижает использование памяти при одновременном повышении вычислительной эффективности. [52]

Математическое представление

Стандартное масштабированное скалярное произведение Внимание

Для матриц: и масштабированное скалярное произведение или внимание QKV определяется как: где обозначает транспонирование , а функция softmax применяется независимо к каждой строке ее аргумента. Матрица содержит запросы, в то время как матрицы совместно содержат неупорядоченный набор пар ключ-значение. Векторы значений в матрице взвешиваются с использованием весов, полученных в результате операции softmax, так что строки матрицы -by- output ограничиваются выпуклой оболочкой точек в , заданной строками . Q ∈ R m × d k , K ∈ R n × d k {\displaystyle \mathbf {Q} \in \mathbb {R^{m\times d_{k}}} ,\mathbf {K} \in \mathbb {R^{n\times d_{k}}} } V ∈ R n × d v {\displaystyle \mathbf {V} \in \mathbb {R^{n\times d_{v}}} } Attention ( Q , K , V ) = softmax ( Q K T d k ) V ∈ R m × d v {\displaystyle {\text{Attention}}(\mathbf {Q} ,\mathbf {K} ,\mathbf {V} )={\text{softmax}}\left({\frac {\mathbf {Q} \mathbf {K} ^{T}}{\sqrt {d_{k}}}}\right)\mathbf {V} \in \mathbb {R} ^{m\times d_{v}}} T {\displaystyle {}^{T}} Q {\displaystyle \mathbf {Q} } m {\displaystyle m} K , V {\displaystyle \mathbf {K} ,\mathbf {V} } n {\displaystyle n} V {\displaystyle \mathbf {V} } m {\displaystyle m} d v {\displaystyle d_{v}} R d v {\displaystyle \mathbb {R} ^{d_{v}}} V {\displaystyle \mathbf {V} }

Чтобы понять свойства инвариантности перестановки и эквивариантности перестановки внимания QKV, [53] пусть и будут матрицами перестановки ; и произвольной матрицей. Функция softmax является эквивариантной перестановки в том смысле, что: A ∈ R m × m {\displaystyle \mathbf {A} \in \mathbb {R} ^{m\times m}} B ∈ R n × n {\displaystyle \mathbf {B} \in \mathbb {R} ^{n\times n}} D ∈ R m × n {\displaystyle \mathbf {D} \in \mathbb {R} ^{m\times n}}

softmax ( A D B ) = A softmax ( D ) B {\displaystyle {\text{softmax}}(\mathbf {A} \mathbf {D} \mathbf {B} )=\mathbf {A} \,{\text{softmax}}(\mathbf {D} )\mathbf {B} }

Заметив, что транспонированная матрица перестановки также является ее обратной, следует, что:

Attention ( A Q , B K , B V ) = A Attention ( Q , K , V ) {\displaystyle {\text{Attention}}(\mathbf {A} \mathbf {Q} ,\mathbf {B} \mathbf {K} ,\mathbf {B} \mathbf {V} )=\mathbf {A} \,{\text{Attention}}(\mathbf {Q} ,\mathbf {K} ,\mathbf {V} )}

что показывает, что внимание QKV эквивариантно относительно переупорядочения запросов (строк ); и инвариантно относительно переупорядочения пар ключ-значение в . Эти свойства наследуются при применении линейных преобразований к входам и выходам блоков внимания QKV. Например, простая функция самовнимания определяется как: Q {\displaystyle \mathbf {Q} } K , V {\displaystyle \mathbf {K} ,\mathbf {V} }

X ↦ Attention ( X T q , X T k , X T v ) {\displaystyle \mathbf {X} \mapsto {\text{Attention}}(\mathbf {X} \mathbf {T} _{q},\mathbf {X} \mathbf {T} _{k},\mathbf {X} \mathbf {T} _{v})}

является перестановочно-эквивариантным относительно переупорядочивания строк входной матрицы нетривиальным образом, поскольку каждая строка вывода является функцией всех строк ввода. Аналогичные свойства сохраняются для multi-head awareness , которое определено ниже. X {\displaystyle X}

Скрытое внимание

Когда внимание QKV используется в качестве строительного блока для авторегрессионного декодера, и когда во время обучения все входные и выходные матрицы имеют строки, используется вариант маскированного внимания : где маска, является строго верхней треугольной матрицей с нулями на и под диагональю и в каждом элементе над диагональю. Выход softmax, также в тогда является нижним треугольным , с нулями во всех элементах над диагональю. Маскирование гарантирует, что для всех , строка выхода внимания не зависит от строки любой из трех входных матриц. Свойства инвариантности перестановок и эквивариантности стандартного внимания QKV не сохраняются для маскированного варианта. n {\displaystyle n} Attention ( Q , K , V ) = softmax ( Q K T d k + M ) V {\displaystyle {\text{Attention}}(\mathbf {Q} ,\mathbf {K} ,\mathbf {V} )={\text{softmax}}\left({\frac {\mathbf {Q} \mathbf {K} ^{T}}{\sqrt {d_{k}}}}+\mathbf {M} \right)\mathbf {V} } M ∈ R n × n {\displaystyle \mathbf {M} \in \mathbb {R} ^{n\times n}} − ∞ {\displaystyle -\infty } R n × n {\displaystyle \mathbb {R} ^{n\times n}} 1 ≤ i < j ≤ n {\displaystyle 1\leq i<j\leq n} i {\displaystyle i} j {\displaystyle j}

Многоголовое внимание

Декодер многоголовый перекрестный внимание

Многоголовочное внимание , где каждая голова вычисляется с помощью внимания QKV как: и , и являются матрицами параметров. MultiHead ( Q , K , V ) = Concat ( head 1 , . . . , head h ) W O {\displaystyle {\text{MultiHead}}(\mathbf {Q} ,\mathbf {K} ,\mathbf {V} )={\text{Concat}}({\text{head}}_{1},...,{\text{head}}_{h})\mathbf {W} ^{O}} head i = Attention ( Q W i Q , K W i K , V W i V ) {\displaystyle {\text{head}}_{i}={\text{Attention}}(\mathbf {Q} \mathbf {W} _{i}^{Q},\mathbf {K} \mathbf {W} _{i}^{K},\mathbf {V} \mathbf {W} _{i}^{V})} W i Q , W i K , W i V {\displaystyle \mathbf {W} _{i}^{Q},\mathbf {W} _{i}^{K},\mathbf {W} _{i}^{V}} W O {\displaystyle \mathbf {W} ^{O}}

Свойства перестановки (стандартного, немаскированного) внимания QKV применяются и здесь. Для матриц перестановки : A , B {\displaystyle \mathbf {A} ,\mathbf {B} }

MultiHead ( A Q , B K , B V ) = A MultiHead ( Q , K , V ) {\displaystyle {\text{MultiHead}}(\mathbf {A} \mathbf {Q} ,\mathbf {B} \mathbf {K} ,\mathbf {B} \mathbf {V} )=\mathbf {A} \,{\text{MultiHead}}(\mathbf {Q} ,\mathbf {K} ,\mathbf {V} )}

из чего мы также видим, что многоголовое самовнимание :

X ↦ MultiHead ( X T q , X T k , X T v ) {\displaystyle \mathbf {X} \mapsto {\text{MultiHead}}(\mathbf {X} \mathbf {T} _{q},\mathbf {X} \mathbf {T} _{k},\mathbf {X} \mathbf {T} _{v})}

является эквивариантным относительно переупорядочения строк входной матрицы . X {\displaystyle X}

Багданау (Добавка) Внимание

Attention ( Q , K , V ) = softmax ( e ) V {\displaystyle {\text{Attention}}(Q,K,V)={\text{softmax}}(e)V} где и и — матрицы обучаемых весов. [41] e = tanh ⁡ ( W Q Q + W K K ) {\displaystyle e=\tanh(W_{Q}Q+W_{K}K)} W Q {\displaystyle W_{Q}} W K {\displaystyle W_{K}}

Внимание (Общее)

Attention ( Q , K , V ) = softmax ( Q W a K T ) V {\displaystyle {\text{Attention}}(Q,K,V)={\text{softmax}}(QW_{a}K^{T})V} где — обучаемая весовая матрица. [42] W a {\displaystyle W_{a}}

Смотрите также

Ссылки

  1. ^ ab Niu, Zhaoyang; Zhong, Guoqiang; Yu, Hui (2021-09-10). «Обзор механизма внимания при глубоком обучении». Neurocomputing . 452 : 48–62 . doi :10.1016/j.neucom.2021.03.091. ISSN  0925-2312.
  2. ^ ab Soydaner, Derya (август 2022 г.). «Механизм внимания в нейронных сетях: откуда он приходит и куда уходит». Neural Computing and Applications . 34 (16): 13371– 13385. arXiv : 2204.13154 . doi : 10.1007/s00521-022-07366-3. ISSN  0941-0643.
  3. ^ Крамер, Артур Ф.; Вигманн, Дуглас А.; Кирлик, Алекс (28.12.2006). «1 Внимание: от истории к применению». Внимание: от теории к практике. Oxford University Press. doi :10.1093/acprof:oso/9780195305722.003.0001. ISBN 978-0-19-530572-2.
  4. ^ Cherry EC (1953). «Некоторые эксперименты по распознаванию речи одним и двумя ушами» (PDF) . Журнал акустического общества Америки . 25 (5): 975– 79. Bibcode :1953ASAJ...25..975C. doi :10.1121/1.1907229. hdl : 11858/00-001M-0000-002A-F750-3 . ISSN  0001-4966.
  5. ^ Бродбент, Д. (1958). Восприятие и коммуникация . Лондон: Pergamon Press.
  6. ^ Коулер, Эйлин; Андерсон, Эрик; Дошер, Барбара; Блейзер, Эрик (1995-07-01). «Роль внимания в программировании саккад». Vision Research . 35 (13): 1897– 1916. doi :10.1016/0042-6989(94)00279-U. ISSN  0042-6989. PMID  7660596.
  7. ^ Фукусима, Кунихико (1987-12-01). «Нейронная сетевая модель для избирательного внимания при распознавании визуальных образов и ассоциативном вспоминании». Applied Optics . 26 (23): 4985– 4992. Bibcode : 1987ApOpt..26.4985F. doi : 10.1364/AO.26.004985. ISSN  0003-6935. PMID  20523477.
  8. ^ Ба, Джимми; Мних, Владимир; Кавукчуоглу, Корай (2015-04-23). ​​«Распознавание нескольких объектов с помощью визуального внимания». arXiv : 1412.7755 [cs.LG].
  9. ^ Кох, Кристоф; Ульман, Шимон (1987). «Сдвиги в селективном зрительном внимании: к базовым нейронным схемам». В Vaina, Lucia M. (ред.). Вопросы интеллекта: концептуальные структуры в когнитивной нейронауке . Дордрехт: Springer Netherlands. стр.  115– 141. doi :10.1007/978-94-009-3833-5_5. ISBN 978-94-009-3833-5. Получено 2024-08-06 .
  10. ^ Itti, L.; Koch, C.; Niebur, E. (ноябрь 1998 г.). «Модель визуального внимания на основе заметности для быстрого анализа сцены». Труды IEEE по анализу образов и машинному интеллекту . 20 (11): 1254– 1259. doi :10.1109/34.730558.
  11. ^ Ивахненко, А. Г. (1973). Кибернетические предсказывающие устройства. CCM Information Corporation.
  12. ^ Ивахненко, АГ ; Григорьевич Лапа, Валентин (1967). Кибернетика и методы прогнозирования. American Elsevier Pub. Co.
  13. ^ Шмидхубер, Юрген (2022). «Аннотированная история современного ИИ и глубокого обучения». arXiv : 2212.11279 [cs.NE].
  14. ^ Джайлс, К. Ли; Максвелл, Том (1987-12-01). «Обучение, инвариантность и обобщение в нейронных сетях высокого порядка». Прикладная оптика . 26 (23): 4972– 4978. doi :10.1364/AO.26.004972. ISSN  0003-6935. PMID  20523475.
  15. ^ Фельдман, JA; Баллард, DH (1982-07-01). «Модели коннекционизма и их свойства». Cognitive Science . 6 (3): 205–254 . doi :10.1016/S0364-0213(82)80001-3. ISSN  0364-0213.
  16. ^ Rumelhart, David E.; Hinton, GE; Mcclelland, James L. (1987-07-29). "Общая структура для параллельной распределенной обработки" (PDF) . В Rumelhart, David E.; Hinton, GE; PDP Research Group (ред.). Параллельная распределенная обработка, том 1: Исследования микроструктуры познания: основы . Кембридж, Массачусетс: MIT Press. ISBN 978-0-262-68053-0.
  17. ^ abc Шмидхубер, Юрген (1992). «Обучение управлению быстрой памятью с весом: альтернатива рекуррентным сетям». Neural Computation . 4 (1): 131– 139. doi :10.1162/neco.1992.4.1.131. S2CID  16683347.
  18. ^ Ха, Дэвид; Дай, Эндрю; Ле, Куок В. (01 декабря 2016 г.). «Гиперсети». arXiv : 1609.09106 [cs.LG].
  19. ^ Кристоф фон дер Мальсбург: Теория корреляции функций мозга. Внутренний отчет 81-2, MPI Biophysical Chemistry, 1981. http://cogprints.org/1380/1/vdM_correlation.pdf См. перепечатку в Models of Neural Networks II, глава 2, страницы 95-119. Springer, Берлин, 1994.
  20. ↑ Джером А. Фельдман, «Динамические связи в нейронных сетях», Биологическая кибернетика, т. 46, № 1, стр. 27-39, декабрь 1982 г.
  21. ^ Хинтон, Джеффри Э.; Плаут, Дэвид К. (1987). «Использование быстрых весов для устранения размытости старых воспоминаний». Труды ежегодного собрания Общества когнитивной науки . 9 .
  22. ^ аб Шлаг, Иманол ; Ириэ, Кадзуки; Шмидхубер, Юрген (2021). «Линейные трансформаторы — тайно быстрые программисты веса». ICML 2021 . Спрингер. С.  9355–9366 .
  23. ^ Шмидхубер, Юрген (1993). «Уменьшение соотношения между сложностью обучения и числом переменных, изменяющихся во времени, в полностью рекуррентных сетях». ICANN 1993. Springer. стр.  460–463 .
  24. ^ Суцкевер, Илья; Виньялс, Ориол; Ле, Куок Вьет (2014). «Последовательное обучение с помощью нейронных сетей». arXiv : 1409.3215 [cs.CL].
  25. ^ Виньялс, Ориол; Тошев, Александр; Бенджио, Сами; Эрхан, Думитру (2015). «Покажи и расскажи: нейронный генератор подписей к изображениям». С.  3156–3164 .
  26. ^ Сюй, Кельвин; Ба, Джимми; Кирос, Райан; Чо, Кёнхён; Курвиль, Аарон; Салахудинов, Руслан; Земель, Рич; Бенджио, Йошуа (2015-06-01). «Покажи, посети и расскажи: генерация подписей к изображениям на основе нейронов с визуальным вниманием». Труды 32-й Международной конференции по машинному обучению . PMLR: 2048–2057 .
  27. ^ ab Багданау, Дмитрий; Чо, Кёнхён; Бенгио, Йошуа (19 мая 2016 г.). «Нейронный машинный перевод путем совместного обучения выравниванию и переводу». arXiv : 1409.0473 [cs.CL].(дата создания 1 сентября 2014 г.)
  28. ^ Парих, Анкур; Тэкстрём, Оскар; Дас, Дипанджан; Ушкорейт, Якоб (2016). «Разложимая модель внимания для вывода на естественном языке». Труды конференции 2016 года по эмпирическим методам в обработке естественного языка . Страудсбург, Пенсильвания, США: Ассоциация компьютерной лингвистики. стр.  2249–2255 . arXiv : 1606.01933 . doi :10.18653/v1/d16-1244.
  29. ^ Грейвс, Алекс; Уэйн, Грег; Рейнольдс, Малкольм; Харли, Тим; Данихелка, Иво; Грабска-Барвинска, Агнешка; Кольменарехо, Серхио Гомес; Грефенстетте, Эдвард; Рамальо, Тиаго; Агапиу, Джон; Бадиа, Адриа Пучдоменек; Герман, Карл Мориц; Звольс, Йори; Островски, Георг; Каин, Адам; Кинг, Хелен; Саммерфилд, Кристофер; Блансом, Фил; Кавуккуоглу, Корай; Хассабис, Демис (12.10.2016). «Гибридные вычисления с использованием нейронной сети с динамической внешней памятью». Nature . 538 (7626): 471– 476. Bibcode :2016Natur.538..471G. doi : 10.1038/nature20101. ISSN  1476-4687. PMID  27732574. S2CID  205251479.
  30. ^ Грейвс, Алекс; Уэйн, Грег; Данигелька, Иво (10 декабря 2014 г.). «Нейронные машины Тьюринга». arXiv : 1410.5401 [cs.NE].
  31. ^ ab Ченг, Цзяньпэн; Донг, Ли; Лапата, Мирелла (2016-09-20). «Сети краткосрочной памяти для машинного чтения». arXiv : 1601.06733 [cs.CL].
  32. ^ ab Zhang, Ruiqi (2024). "Обученные трансформеры изучают линейные модели в контексте" (PDF) . Журнал исследований машинного обучения 1-55 . 25 . arXiv : 2306.09927 .
  33. ^ ab Rende, Riccardo (2024). «Картирование механизмов внимания в обобщенной модели Поттса». Physical Review Research . 6 (2): 023057. arXiv : 2304.07235 . Bibcode : 2024PhRvR...6b3057R. doi : 10.1103/PhysRevResearch.6.023057.
  34. ^ ab He, Bobby (2023). «Упрощение блоков трансформаторов». arXiv : 2311.01906 [cs.LG].
  35. ^ ab Nguyen, Timothy (2024). «Понимание трансформаторов с помощью статистики N-грамм». arXiv : 2407.12034 [cs.CL].
  36. ^ ab "Трансформаторные схемы". transformer-circuits.pub .
  37. ^ ab Transformer Neural Network Derived From Scratch. 2023. Событие происходит в 05:30 . Получено 2024-04-07 .
  38. ^ ab Charton, François (2023). «Изучение наибольшего общего делителя: объяснение предсказаний трансформатора». arXiv : 2308.15594 [cs.LG].
  39. ^ Бритц, Денни; Голди, Анна; Луонг, Минь-Тхань; Ле, Куок (2017-03-21). «Массовое исследование архитектур нейронного машинного перевода». arXiv : 1703.03906 [cs.CV].
  40. ^ "Pytorch.org seq2seq tutorial" . Получено 2 декабря 2021 г. .
  41. ^ ab Багданау, Дмитрий; Чо, Кёнхён; Бенгио, Йошуа (2014). «Нейронный машинный перевод путем совместного обучения выравниванию и переводу». arXiv : 1409.0473 [cs.CL].
  42. ^ abc Luong, Minh-Thang (2015-09-20). «Эффективные подходы к нейронному машинному переводу на основе внимания». arXiv : 1508.04025v5 [cs.CL].
  43. ^ «Изучение позиционного внимания для последовательной рекомендации». catalyzex.com .
  44. ^ Чжу, Сичжоу; Чэн, Дачжи; Чжан, Чжэн; Линь, Стивен; Дай, Цзифэн (2019). «Эмпирическое исследование механизмов пространственного внимания в глубоких сетях». Международная конференция IEEE/CVF по компьютерному зрению (ICCV) 2019 г. стр.  6687–6696 . arXiv : 1904.05873 . doi :10.1109/ICCV.2019.00679. ISBN 978-1-7281-4803-8. S2CID  118673006.
  45. ^ Ху, Цзе; Шен, Ли; Сан, Ганг (2018). «Сети сжатия и возбуждения». Конференция IEEE/CVF 2018 года по компьютерному зрению и распознаванию образов . стр.  7132–7141 . arXiv : 1709.01507 . doi :10.1109/CVPR.2018.00745. ISBN 978-1-5386-6420-9. S2CID  206597034.
  46. ^ У, Санхён; Пак, Чончан; Ли, Джун-Ён; Квеон, Ин Со (18 июля 2018 г.). «CBAM: Модуль внимания сверточного блока». arXiv : 1807.06521 [cs.CV].
  47. ^ Георгеску, Мариана-Юлиана; Ионеску, Раду Тудор; Мирон, Андреа-Юлиана; Савенку, Оливиан; Ристеа, Николае-Каталин; Верга, Николае; Хан, Фахад Шахбаз (12 октября 2022 г.). «Мультимодальное многоголовое сверточное внимание с различными размерами ядер для сверхразрешения медицинских изображений». arXiv : 2204.04218 [eess.IV].
  48. ^ Нил Роудс (2021). CS 152 NN—27: Внимание: ключи, запросы и значения. Событие происходит в 06:30 . Получено 22.12.2021 .
  49. ^ Альфредо Канциани и Янн Лекун (2021). Курс глубокого обучения в Нью-Йоркском университете, весна 2020 г. Событие происходит в 05:30 . Получено 22.12.2021 .
  50. ^ Альфредо Канциани и Янн Лекун (2021). Курс глубокого обучения Нью-Йоркского университета, весна 2020 г. Событие происходит в 20:15 . Получено 22.12.2021 .
  51. ^ Робертсон, Шон. «НЛП с нуля: перевод с помощью сети последовательностей и внимания». pytorch.org . Получено 22.12.2021 .
  52. ^ Миттал, Ааюш (2024-07-17). "Внимание: Революция в эффективности трансформаторов". Unite.AI . Получено 2024-11-16 .
  53. ^ Ли, Джухо; Ли, Юнхо; Ким, Чонгтек; Косиорек, Адам Р.; Чой, Сынджин; Тех, Йи Уай (2018). «Трансформатор множеств: структура для нейронных сетей, инвариантных к перестановкам, основанных на внимании». arXiv : 1810.00825 [cs.LG].
  • Олах, Крис; Картер, Шан (8 сентября 2016 г.). «Внимание и расширенные рекуррентные нейронные сети». Distill . 1 (9). Рабочая группа Distill. doi :10.23915/distill.00001.
  • Дэн Джурафски и Джеймс Х. Мартин (2022) Обработка речи и языка (черновик 3-го издания, январь 2022 г.), гл. 10.4 Внимание и гл. 9.7 Сети внутреннего внимания: Трансформаторы
  • Алекс Грейвс (4 мая 2020 г.), Внимание и память в глубоком обучении (видеолекция), DeepMind / UCL , через YouTube
Retrieved from "https://en.wikipedia.org/w/index.php?title=Attention_(machine_learning)&oldid=1268130109"