Эксплуатационная характеристика приемника
This article needs additional citations for verification. (September 2023) |
Кривая рабочей характеристики приемника , или кривая ROC , представляет собой графический график , иллюстрирующий эффективность модели бинарного классификатора (может использоваться и для многоклассовой классификации) при различных пороговых значениях.
Кривая ROC представляет собой график зависимости истинно положительного результата (TPR) от ложноположительного результата (FPR) при каждой настройке порогового значения.
ROC также можно рассматривать как график статистической мощности как функции ошибки типа I правила принятия решения (когда производительность рассчитывается только на основе выборки из совокупности, ее можно рассматривать как оценщики этих величин). Таким образом, ROC-кривая представляет собой чувствительность как функцию частоты ложных срабатываний .
Учитывая, что известны распределения вероятностей как для истинно положительных, так и для ложно положительных результатов, кривая ROC получается как кумулятивная функция распределения (CDF, площадь под распределением вероятностей от до порога дискриминации) вероятности обнаружения по оси Y в зависимости от CDF вероятности ложно положительных результатов по оси X.
Анализ ROC предоставляет инструменты для выбора потенциально оптимальных моделей и отбрасывания неоптимальных независимо от (и до указания) контекста затрат или распределения классов. Анализ ROC напрямую и естественным образом связан с анализом затрат/выгод принятия диагностических решений .
Терминология
Истинно-положительный показатель также известен как чувствительность или вероятность обнаружения . [1] Ложно-положительный показатель также известен как вероятность ложной тревоги [1] и равен (1 − специфичность ). ROC также известен как относительная кривая рабочей характеристики, поскольку он представляет собой сравнение двух рабочих характеристик (TPR и FPR) при изменении критерия. [2]
История
Кривая ROC была впервые разработана инженерами-электриками и инженерами-радиолокаторами во время Второй мировой войны для обнаружения вражеских объектов на полях сражений, начиная с 1941 года, что и привело к ее названию («рабочая характеристика приемника»). [3]
Вскоре он был введен в психологию для учета перцептивного обнаружения стимулов. Анализ ROC использовался в медицине , радиологии , биометрии , прогнозировании стихийных бедствий , [4] метеорологии , [5] оценке эффективности моделей [6] и других областях в течение многих десятилетий и все чаще используется в исследованиях машинного обучения и добычи данных .
Основная концепция
Модель классификации ( классификатор или диагностика [7] ) — это отображение экземпляров между определенными классами/группами. Поскольку результат классификатора или диагностики может быть произвольным действительным значением (непрерывный вывод), граница классификатора между классами должна определяться пороговым значением (например, чтобы определить, есть ли у человека гипертония на основе измерения артериального давления ). Или это может быть дискретная метка класса, указывающая на один из классов.
Рассмотрим задачу двухклассового прогнозирования ( бинарная классификация ), в которой результаты помечены как положительные ( p ) или отрицательные ( n ). Существует четыре возможных результата бинарного классификатора. Если результат прогноза равен p , а фактическое значение также равно p , то это называется истинно положительным (TP); однако если фактическое значение равно n , то это называется ложноположительным ( FP). И наоборот, истинно отрицательный (TN) результат имеет место, когда и результат прогноза, и фактическое значение равны n , а ложноотрицательный (FN) результат прогноза равен n , а фактическое значение равно p .
Чтобы получить подходящий пример в реальной проблеме, рассмотрим диагностический тест, который пытается определить, есть ли у человека определенное заболевание. Ложноположительный результат в этом случае возникает, когда у человека положительный результат теста, но на самом деле у него нет заболевания. Ложноотрицательный результат, с другой стороны, возникает, когда у человека отрицательный результат теста, предполагающий, что он здоров, хотя на самом деле у него есть заболевание.
Рассмотрим эксперимент с P положительными примерами и N отрицательными примерами для некоторого условия. Четыре результата можно сформулировать в виде таблицы сопряженности 2×2 или матрицы путаницы следующим образом:
| Прогнозируемое состояние | Источники: [8] [9] [10] [11] [12] [13] [14] [15] | ||||
| Общая численность населения = P + N | Прогнозируемый положительный (ПП) | Прогнозируемый отрицательный (PN) | Информированность , букмекерская информированность (БМ) = TPR + TNR − 1 | Порог распространенности (PT) = √ TPR × FPR - FPR/ТПР - ФПР | |
Фактическое состояние | Положительный (P) [a] | Истинно положительный (TP), удар [b] | Ложноотрицательный результат (ЛО), промах, недооценка | Истинно положительный процент (TPR), отзыв , чувствительность (SEN), вероятность обнаружения, процент попаданий, мощность = ТП/П = 1 − ФНР | Ложноотрицательный коэффициент (ЛКО), коэффициент ошибок типа II [c] = ФН/П = 1 − ТПР |
| Отрицательно (Н) [д] | Ложноположительный результат (ЛП), ложная тревога, переоценка | Истинно отрицательный (TN), правильное отклонение [e] | Коэффициент ложных срабатываний (FPR), вероятность ложной тревоги, ошибка типа I [f] = ФП/Н = 1 − ТНР | Истинно отрицательный показатель (TNR), специфичность (SPC), селективность = ТН/Н = 1 − ФПР | |
| Распространенность = П/П + Н | Положительная прогностическая ценность (PPV), точность = ТП/ПП = 1 − ФДР | Коэффициент ложного пропуска (FOR) = ФН/ПН = 1 − ЧПС | Положительное отношение правдоподобия (LR+) = ТПР/ФПР | Отрицательное отношение правдоподобия (LR−) = ФНР/ТНР | |
| Точность (ACC) = ТП + ТН/П + Н | Коэффициент ложных срабатываний (FDR) = ФП/ПП = 1 − ППЦ | Отрицательная прогностическая ценность (NPV) = ТН/ПН = 1 − ДЛЯ | Маркированность (МК), дельтаП (Δp) = PPV + NPV − 1 | Диагностическое отношение шансов (DOR) = ЛР+/ЛР− | |
| Сбалансированная точность (BA) = ТПР + ТНР/2 | F 1 оценка = 2 PPV × TPR/ППВ + ТПР = 2 ТП/2 ТП + ФП + ФН | Индекс Фаулкса–Мэллоуза (FM) = √ PPV × TPR | Коэффициент корреляции Мэтьюса (MCC) = √ TPR × TNR × PPV × NPV - √ FNR × FPR × FOR × FDR | Оценка угрозы (TS), индекс критического успеха (CSI), индекс Жаккара = ТП/ТП + ФН + ФП | |
- ^ количество реальных положительных случаев в данных
- ^ Результат теста, который правильно указывает на наличие состояния или характеристики.
- ^ Ошибка типа II: результат теста, который ошибочно указывает на отсутствие определенного условия или атрибута.
- ^ количество реальных отрицательных случаев в данных
- ^ Результат теста, который правильно указывает на отсутствие состояния или характеристики.
- ^ Ошибка типа I: результат теста, который ошибочно указывает на наличие определенного состояния или атрибута.
пространство РПЦ


Таблица сопряженности может вывести несколько «метрик» оценки (см. инфобокс). Для построения ROC-кривой необходимы только истинно положительные результаты (TPR) и ложноположительные результаты (FPR) (как функции некоторого параметра классификатора). TPR определяет, сколько правильных положительных результатов происходит среди всех положительных образцов, доступных во время теста. FPR, с другой стороны, определяет, сколько неправильных положительных результатов происходит среди всех отрицательных образцов, доступных во время теста.
Пространство ROC определяется FPR и TPR как оси x и y соответственно, которые отображают относительные компромиссы между истинным положительным результатом (выгоды) и ложным положительным результатом (затраты). Поскольку TPR эквивалентно чувствительности, а FPR равно 1 − специфичность , график ROC иногда называют графиком чувствительности против (1 − специфичность). Каждый результат прогноза или пример матрицы путаницы представляет одну точку в пространстве ROC.
Наилучший возможный метод прогнозирования даст точку в верхнем левом углу или координату (0,1) пространства ROC, что представляет 100% чувствительность (без ложных отрицательных результатов) и 100% специфичность (без ложных положительных результатов). Точка (0,1) также называется идеальной классификацией . Случайная догадка даст точку вдоль диагональной линии (так называемой линии отсутствия дискриминации ) от нижнего левого до верхнего правого угла (независимо от положительных и отрицательных базовых ставок ). [16] Интуитивным примером случайной догадки является решение, принимаемое путем подбрасывания монет. По мере увеличения размера выборки точка ROC случайного классификатора стремится к диагональной линии. В случае сбалансированной монеты она будет стремиться к точке (0,5, 0,5).
Диагональ делит пространство ROC. Точки над диагональю представляют хорошие результаты классификации (лучше случайных); точки под линией представляют плохие результаты (хуже случайных). Обратите внимание, что вывод постоянно плохого предиктора можно просто инвертировать, чтобы получить хороший предиктор.
Рассмотрим четыре результата прогнозирования из 100 положительных и 100 отрицательных случаев:
| А | Б | С | С′ | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
| ||||||||||||||||||||||||||||||||||||
| ОПЗ = 0,63 | ОПЗ = 0,77 | ОПЗ = 0,24 | ОПЗ = 0,76 | ||||||||||||||||||||||||||||||||||||
| ФПР = 0,28 | ФПР = 0,77 | ФПР = 0,88 | ФПР = 0,12 | ||||||||||||||||||||||||||||||||||||
| ППЗ = 0,69 | ППЗ = 0,50 | ППЗ = 0,21 | ППЗ = 0,86 | ||||||||||||||||||||||||||||||||||||
| Ф1 = 0,66 | Ф1 = 0,61 | Ф1 = 0,23 | Ф1 = 0,81 | ||||||||||||||||||||||||||||||||||||
| АСС = 0,68 | АСС = 0,50 | АСС = 0,18 | АСС = 0,82 |
Графики четырех результатов выше в пространстве ROC приведены на рисунке. Результат метода A ясно показывает лучшую предсказательную силу среди A , B , и C . Результат B лежит на линии случайного предположения (диагональная линия), и в таблице можно увидеть, что точность B составляет 50%. Однако, когда C зеркально отображается относительно центральной точки (0,5, 0,5), результирующий метод C′ даже лучше, чем A . Этот зеркальный метод просто меняет предсказания любого метода или теста, создавшего таблицу сопряженности C . Хотя исходный метод C имеет отрицательную предсказательную силу, простое изменение его решений приводит к новому предсказательному методу C ′, который имеет положительную предсказательную силу. Когда метод C предсказывает p или n , метод C′ предскажет n или p , соответственно. Таким образом, тест C′ будет работать лучше всего. Чем ближе результат из таблицы сопряженности к верхнему левому углу, тем лучше он предсказывает, но расстояние от линии случайного предположения в любом направлении является лучшим индикатором того, насколько предсказательной силой обладает метод. Если результат находится ниже линии (т. е. метод хуже случайного предположения), все предсказания метода должны быть обращены вспять, чтобы использовать его силу, тем самым перемещая результат выше линии случайного предположения.
Кривые в пространстве ROC
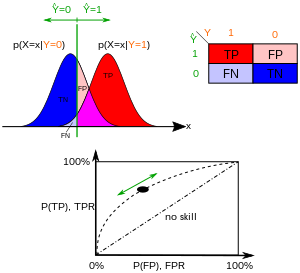
В бинарной классификации предсказание класса для каждого экземпляра часто делается на основе непрерывной случайной величины , которая является «оценкой», вычисленной для экземпляра (например, предполагаемая вероятность в логистической регрессии). При заданном пороговом параметре экземпляр классифицируется как «положительный», если , и «отрицательный» в противном случае. следует плотности вероятности , если экземпляр действительно принадлежит к классу «положительный», и если в противном случае. Таким образом, истинно положительный показатель определяется как , а ложноположительный показатель определяется как . Кривая ROC параметрически строится в зависимости от того, какой параметр является переменным.
Например, представьте, что уровни белка в крови у больных и здоровых людей распределены нормально со средними значениями 2 г / дл и 1 г/дл соответственно. Медицинский тест может измерить уровень определенного белка в образце крови и классифицировать любое число выше определенного порога как указание на заболевание. Экспериментатор может отрегулировать порог (зеленая вертикальная линия на рисунке), что, в свою очередь, изменит уровень ложноположительных результатов. Увеличение порога приведет к меньшему количеству ложноположительных результатов (и большему количеству ложноотрицательных результатов), что соответствует движению кривой влево. Фактическая форма кривой определяется тем, насколько перекрываются два распределения.
Критика

Несколько исследований критикуют определенные применения кривой ROC и ее площади под кривой в качестве измерений для оценки бинарных классификаций, когда они не охватывают информацию, относящуюся к применению. [18] [17] [19] [20] [21]
Основная критика ROC-кривой, описанной в этих исследованиях, касается включения областей с низкой чувствительностью и низкой специфичностью (оба ниже 0,5) для расчета общей площади под кривой (AUC) [19] , как показано на графике справа.
По мнению авторов этих исследований, эта часть площади под кривой (с низкой чувствительностью и низкой специфичностью) касается матриц путаницы, где бинарные предсказания дают плохие результаты, и поэтому не должна включаться в оценку общей производительности. Более того, эта часть AUC указывает на пространство с высоким или низким порогом матрицы путаницы, которое редко представляет интерес для ученых, выполняющих бинарную классификацию в любой области. [19]
Еще одно замечание в адрес ROC и его площади под кривой заключается в том, что они ничего не говорят о точности и отрицательной прогностической ценности. [17]
Высокий ROC AUC, например 0,9, может соответствовать низким значениям точности и отрицательной предсказательной ценности, таким как 0,2 и 0,1 в диапазоне [0, 1]. Если кто-то выполнил бинарную классификацию, получил ROC AUC 0,9 и решил сосредоточиться только на этой метрике, он может чрезмерно оптимистично полагать, что его бинарный тест был превосходным. Однако, если этот человек взглянет на значения точности и отрицательной предсказательной ценности, он может обнаружить, что их значения низкие.
ROC AUC суммирует чувствительность и специфичность, но не дает информации о точности и отрицательной прогностической ценности. [17]
Дальнейшие интерпретации
Иногда ROC используется для создания сводной статистики. Распространенные версии:
- пересечение кривой ROC с линией под углом 45 градусов, перпендикулярной линии отсутствия дискриминации — точка равновесия, где Чувствительность = Специфичность
- пересечение кривой ROC с касательной под углом 45 градусов, параллельной линии отсутствия дискриминации, которая находится ближе всего к точке без ошибок (0,1) – также называется статистикой J Юдена и обобщается как Информированность [ необходима ссылка ]
- Площадь между кривой ROC и линией недискриминации, умноженная на два, называется коэффициентом Джини , особенно в контексте кредитного скоринга . [22] Его не следует путать с мерой статистической дисперсии, также называемой коэффициентом Джини .
- область между полной кривой ROC и треугольной кривой ROC, включающая только (0,0), (1,1) и одну выбранную рабочую точку – Согласованность [23]
- площадь под кривой ROC, или «AUC» («площадь под кривой»), или A' (произносится как «а-прим»), [24] или «c-статистика» («статистика соответствия»). [25]
- индекс чувствительности d′ (произносится как «d-prime»), расстояние между средним значением распределения активности в системе в условиях наличия только шума и ее распределением в условиях наличия только сигнала, деленное на их стандартное отклонение , при условии, что оба эти распределения являются нормальными с одинаковым стандартным отклонением. При этих предположениях форма ROC полностью определяется d′ .
Однако любая попытка суммировать кривую ROC в одно число приводит к потере информации о закономерностях компромиссов конкретного алгоритма дискриминатора.
Вероятностная интерпретация
Площадь под кривой (часто называемая просто AUC) равна вероятности того, что классификатор оценит случайно выбранный положительный экземпляр выше, чем случайно выбранный отрицательный (предполагая, что «положительный» ранг выше, чем «отрицательный»). [26] Другими словами, когда дан один случайно выбранный положительный экземпляр и один случайно выбранный отрицательный экземпляр, AUC — это вероятность того, что классификатор сможет сказать, какой из них какой.
Это можно увидеть следующим образом: площадь под кривой определяется выражением (границы интеграла меняются местами, поскольку больший порог имеет меньшее значение на оси x )
где — оценка положительного случая, — оценка отрицательного случая, а и — плотности вероятности, определенные в предыдущем разделе.
Если и следует двум гауссовым распределениям, то .
Площадь под кривой
Можно показать, что AUC тесно связана с U Манна-Уитни , [27] [28] , который проверяет, ранжируются ли положительные результаты выше, чем отрицательные. Для предиктора несмещенная оценка его AUC может быть выражена следующей статистикой Вилкоксона-Манна-Уитни : [29]
где обозначает индикаторную функцию , которая возвращает 1, в противном случае возвращает 0; — множество отрицательных примеров, а — множество положительных примеров.
В контексте кредитного скоринга часто используется измененная версия AUC:
.
называется индексом Джини или коэффициентом Джини, [30] но его не следует путать с мерой статистической дисперсии, которая также называется коэффициентом Джини . является частным случаем D Сомерса .
Также принято вычислять площадь под выпуклой оболочкой ROC (ROC AUCH = ROCH AUC), поскольку любая точка на отрезке линии между двумя результатами прогнозирования может быть получена путем случайного использования одной или другой системы с вероятностями, пропорциональными относительной длине противоположного компонента отрезка. [31] Также возможно инвертировать вогнутости — как на рисунке, худшее решение может быть отражено, чтобы стать лучшим решением; вогнутости могут быть отражены в любом отрезке линии, но эта более экстремальная форма слияния с гораздо большей вероятностью приведет к переобучению данных. [32]
Сообщество машинного обучения чаще всего использует статистику ROC AUC для сравнения моделей. [33] Эта практика была подвергнута сомнению, поскольку оценки AUC довольно шумные и страдают от других проблем. [34] [35] [36] Тем не менее, согласованность AUC как меры агрегированной эффективности классификации была подтверждена с точки зрения равномерного распределения скорости, [37] и AUC была связана с рядом других показателей эффективности, таких как оценка Брайера . [38]
Другая проблема с ROC AUC заключается в том, что сведение ROC-кривой к одному числу игнорирует тот факт, что речь идет о компромиссах между различными системами или нанесенными на график точками производительности, а не о производительности отдельной системы, а также игнорирует возможность исправления вогнутости, поэтому рекомендуются связанные альтернативные меры, такие как Информированность [ требуется ссылка ] или DeltaP. [23] [39] Эти меры по сути эквивалентны индексу Джини для одной точки прогнозирования с DeltaP' = Информированность = 2AUC-1, в то время как DeltaP = Маркированность представляет собой дуал (т. е. прогнозирование прогноза из реального класса), а их геометрическое среднее является коэффициентом корреляции Мэтьюза [ требуется ссылка ]
В то время как ROC AUC варьируется от 0 до 1 — с неинформативным классификатором, дающим 0,5 — альтернативные меры, известные как Информированность , [ требуется ссылка ] Определенность [23] и Коэффициент Джини (в случае одиночной параметризации или одиночной системы) [ требуется ссылка ] имеют то преимущество, что 0 представляет собой случайное выполнение, в то время как 1 представляет собой идеальное выполнение, а −1 представляет собой «извращенный» случай полной информированности, всегда дающий неправильный ответ. [40] Приведение случайного выполнения к 0 позволяет интерпретировать эти альтернативные шкалы как статистику Каппы. Было показано, что информированность имеет желаемые характеристики для машинного обучения по сравнению с другими распространенными определениями Каппы, такими как Каппа Коэна и Каппа Флейсса . [ требуется ссылка ] [41]
Иногда может быть полезнее взглянуть на определенную область кривой ROC, а не на всю кривую. Можно вычислить частичную AUC . [42] Например, можно сосредоточиться на области кривой с низким уровнем ложноположительных результатов, которая часто представляет основной интерес для тестов скрининга населения. [43] Другой распространенный подход к задачам классификации, в которых P ≪ N (распространенный в приложениях биоинформатики), заключается в использовании логарифмической шкалы для оси x . [44]
Площадь ROC под кривой также называется c-статистикой или c-статистикой . [45]
Другие меры

Общая операционная характеристика (TOC) также характеризует диагностическую способность, раскрывая при этом больше информации, чем ROC. Для каждого порога ROC раскрывает два соотношения, TP/(TP + FN) и FP/(FP + TN). Другими словами, ROC раскрывает и . С другой стороны, TOC показывает общую информацию в таблице сопряженности для каждого порога. [46] Метод TOC раскрывает всю информацию, которую предоставляет метод ROC, плюс дополнительную важную информацию, которую ROC не раскрывает, то есть размер каждой записи в таблице сопряженности для каждого порога. TOC также предоставляет популярную AUC ROC. [47]

Эти рисунки представляют собой кривые TOC и ROC, использующие те же данные и пороговые значения. Рассмотрим точку, которая соответствует пороговому значению 74. Кривая TOC показывает количество попаданий, которое равно 3, и, следовательно, количество промахов, которое равно 7. Кроме того, кривая TOC показывает, что количество ложных тревог равно 4, а количество правильных отклонений равно 16. В любой заданной точке кривой ROC можно почерпнуть значения для отношений и . Например, при пороговом значении 74 очевидно, что координата x равна 0,2, а координата y равна 0,3. Однако этих двух значений недостаточно для построения всех записей базовой таблицы сопряженности два на два.
График компромисса ошибок обнаружения
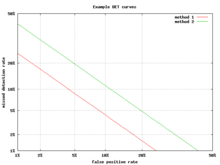
Альтернативой кривой ROC является график компромисса между ошибкой обнаружения (DET), который отображает частоту ложных отрицательных результатов (пропущенных обнаружений) и частоту ложных положительных результатов (ложных тревог) на нелинейно преобразованных осях x и y. Функция преобразования является функцией квантиля нормального распределения, т. е. обратной кумулятивному нормальному распределению. По сути, это то же самое преобразование, что и zROC, ниже, за исключением того, что используется дополнение частоты попаданий, частота промахов или частота ложных отрицательных результатов. Эта альтернатива тратит большую площадь графика на интересующую область. Большая часть области ROC не представляет особого интереса; в первую очередь нас интересует область, примыкающая к оси y , и верхний левый угол, который из-за использования частоты промахов вместо ее дополнения, частоты попаданий, является нижним левым углом на графике DET. Кроме того, графики DET обладают полезным свойством линейности и линейного порогового поведения для нормальных распределений. [48] График DET широко используется в сообществе автоматического распознавания говорящего , где впервые было использовано название DET. Анализ производительности ROC в графиках с этой деформацией осей использовался психологами в исследованиях восприятия в середине 20-го века, [ требуется ссылка ], где это было названо «бумагой двойной вероятности». [49]
Z-оценка
Если к кривой ROC применить стандартную оценку , кривая преобразуется в прямую линию. [50] Эта z-оценка основана на нормальном распределении со средним значением, равным нулю, и стандартным отклонением, равным единице. В теории силы памяти необходимо предположить, что zROC не только линейна, но и имеет наклон 1,0. Нормальное распределение целей (изученных объектов, которые субъекты должны вспомнить) и приманок (неизученных объектов, которые субъекты пытаются вспомнить) является фактором, заставляющим zROC быть линейной.
Линейность кривой zROC зависит от стандартных отклонений распределения силы цели и приманки. Если стандартные отклонения равны, наклон будет равен 1,0. Если стандартное отклонение распределения силы цели больше стандартного отклонения распределения силы приманки, то наклон будет меньше 1,0. В большинстве исследований было обнаружено, что наклоны кривой zROC постоянно опускаются ниже 1, обычно между 0,5 и 0,9. [51] Многие эксперименты дали наклон zROC 0,8. Наклон 0,8 подразумевает, что изменчивость распределения силы цели на 25% больше, чем изменчивость распределения силы приманки. [52]
Другая используемая переменная — d' (d prime) (обсуждалась выше в разделе «Другие меры»), которую можно легко выразить через z-значения. Хотя d ' — это часто используемый параметр, следует признать, что он имеет значение только при строгом соблюдении очень сильных предположений теории прочности, сделанных выше. [53]
Z-оценка кривой ROC всегда линейна, как и предполагалось, за исключением особых ситуаций. Модель знакомства-воспоминания Йонелинаса представляет собой двумерный отчет об узнавании памяти. Вместо того, чтобы субъект просто отвечал «да» или «нет» на определенный ввод, субъект дает вводу ощущение знакомства, которое работает как исходная кривая ROC. Однако, что меняется, так это параметр для Воспоминания (R). Воспоминание предполагается как «все или ничего», и оно превосходит знакомство. Если бы не было компонента воспоминания, zROC имел бы прогнозируемый наклон 1. Однако при добавлении компонента воспоминания кривая zROC будет вогнутой вверх с уменьшенным наклоном. Эта разница в форме и наклоне является результатом добавленного элемента изменчивости из-за припоминания некоторых элементов. Пациенты с антероградной амнезией не способны вспомнить, поэтому их кривая zROC Йонелинаса имела бы наклон, близкий к 1,0. [54]
История
Кривая ROC впервые была использована во время Второй мировой войны для анализа радиолокационных сигналов , прежде чем она была применена в теории обнаружения сигналов . [55] После атаки на Перл-Харбор в 1941 году военные США начали новые исследования, чтобы улучшить прогнозирование правильно обнаруженных японских самолетов по их радиолокационным сигналам. Для этих целей они измерили способность оператора радиолокационного приемника делать эти важные различия, что было названо рабочей характеристикой приемника. [56]
В 1950-х годах ROC-кривые использовались в психофизике для оценки обнаружения слабых сигналов человеком (а иногда и животными). [55] В медицине ROC-анализ широко использовался при оценке диагностических тестов . [57] [58] ROC-кривые также широко используются в эпидемиологии и медицинских исследованиях и часто упоминаются в сочетании с доказательной медициной . В радиологии ROC-анализ является распространенным методом оценки новых методов радиологии. [59] В социальных науках ROC-анализ часто называют коэффициентом точности ROC, распространенным методом оценки точности моделей вероятности по умолчанию. ROC-кривые широко используются в лабораторной медицине для оценки диагностической точности теста, выбора оптимального порогового значения теста и сравнения диагностической точности нескольких тестов.
ROC-кривые также оказались полезными для оценки методов машинного обучения . Первое применение ROC в машинном обучении было сделано Спэкманом, который продемонстрировал ценность ROC-кривых при сравнении и оценке различных алгоритмов классификации . [60]
Кривые ROC также используются для проверки прогнозов в метеорологии. [61]
Радар в деталях
Как уже упоминалось, кривые ROC имеют решающее значение для работы и теории радара . Сигналы, полученные на приемной станции, отраженные целью, часто имеют очень низкую энергию по сравнению с уровнем шума . Отношение сигнала к шуму является важным показателем при определении того, будет ли обнаружена цель. Это отношение сигнала к шуму напрямую коррелирует с рабочими характеристиками приемника всей радиолокационной системы, которые используются для количественной оценки возможностей радиолокационной системы.
Рассмотрим разработку радиолокационной системы. Спецификация возможностей системы может быть предоставлена в терминах вероятности обнаружения, , с определенным допуском ложных тревог, . Упрощенное приближение требуемого отношения сигнал/шум на приемной станции может быть рассчитано путем решения [62]
для отношения сигнал/шум . Здесь не в децибелах , как это принято во многих радиолокационных приложениях. Преобразование в децибелы осуществляется через . Из этого рисунка можно решить общие записи в уравнении дальности действия радара (с коэффициентами шума) для оценки требуемой эффективной излучаемой мощности .
ROC-кривые за пределами бинарной классификации
Расширение кривых ROC для задач классификации с более чем двумя классами является громоздким. Два распространенных подхода для случаев, когда есть несколько классов, это (1) усреднение по всем парным значениям AUC [63] и (2) вычисление объема под поверхностью (VUS). [64] [65] Чтобы усреднить по всем парным классам, вычисляется AUC для каждой пары классов, используя только примеры из этих двух классов, как если бы не было других классов, а затем усредняются эти значения AUC по всем возможным парам. Когда есть c классов, будет c ( c − 1) / 2 возможных пар классов.
Подход объема под поверхностью предполагает построение гиперповерхности, а не кривой, а затем измерение гиперобъема под этой гиперповерхностью. Каждое возможное правило принятия решения, которое можно использовать для классификатора для c классов, можно описать в терминах его истинно положительных показателей (TPR 1 , . . . , TPR c ) . Именно этот набор показателей определяет точку, а набор всех возможных правил принятия решения дает облако точек, которые определяют гиперповерхность. При таком определении VUS — это вероятность того, что классификатор сможет правильно пометить все c примеров, когда ему дан набор, содержащий один случайно выбранный пример из каждого класса. Реализация классификатора, который знает, что его входной набор состоит из одного примера из каждого класса, может сначала вычислить оценку соответствия для каждой из c 2 возможных пар примера с классом, а затем применить венгерский алгоритм для максимизации суммы c выбранных оценок по всем c ! возможным способам назначения ровно одного примера каждому классу.
Учитывая успех кривых ROC для оценки моделей классификации, также было исследовано расширение кривых ROC для других контролируемых задач. Известными предложениями для проблем регрессии являются так называемые кривые характеристики ошибки регрессии (REC) [66] и кривые ROC регрессии (RROC). [67] В последнем случае кривые RROC становятся чрезвычайно похожими на кривые ROC для классификации с понятиями асимметрии, доминирования и выпуклой оболочки. Кроме того, площадь под кривыми RROC пропорциональна дисперсии ошибки регрессионной модели.
Смотрите также
Ссылки
- ^ ab "Анализ производительности детектора с использованием ROC-кривых - пример MATLAB и Simulink". www.mathworks.com . Получено 11 августа 2016 г.
- ^ Swets, John A.; Теория обнаружения сигналов и ROC-анализ в психологии и диагностике: сборник статей, Lawrence Erlbaum Associates, Mahwah, NJ, 1996
- ^ Юнге, MR; Деттори, JR (3 мая 2024 г.). «ROC Solid: кривые характеристик приемника-оператора (ROC) как основа для лучших диагностических тестов». Global Spine Journal . 8 (4): 424–429. doi :10.1177/2192568218778294. PMC 6022965. PMID 29977728 .
- ^ Перес, DJ; Кансельер, A. (2014-12-08). «Вывод и оценка порогов возникновения оползней с помощью подхода Монте-Карло». Hydrol. Earth Syst. Sci . 18 (12): 4913–4931. Bibcode :2014HESS...18.4913P. doi : 10.5194/hess-18-4913-2014 . ISSN 1607-7938.
- ^ Мерфи, Аллан Х. (1996-03-01). «Дело Финли: знаковое событие в истории проверки прогнозов». Погода и прогнозирование . 11 (1): 3–20. Bibcode : 1996WtFor..11....3M. doi : 10.1175/1520-0434(1996)011<0003:tfaase>2.0.co;2 . ISSN 0882-8156.
- ^ Перес, DJ; Юппа, C.; Кавалларо, L.; Канчеллиер, A.; Фоти, E. (2015-10-01). «Значительное расширение записи высоты волны с помощью нейронных сетей и повторного анализа данных о ветре». Ocean Modelling . 94 : 128–140. Bibcode : 2015OcMod..94..128P. doi : 10.1016/j.ocemod.2015.08.002.
- ^ Сушкова, Ольга; Морозов, Алексей; Габова, Александра; Карабанов, Алексей; Иллариошкин, Сергей (2021). "Статистический метод разведочного анализа данных на основе двумерных и трехмерных диаграмм площади под кривой: исследование болезни Паркинсона". Датчики . 21 (14): 4700. Bibcode :2021Senso..21.4700S. doi : 10.3390/s21144700 . PMC 8309570 . PMID 34300440.
- ^ Фосетт, Том (2006). «Введение в ROC-анализ» (PDF) . Pattern Recognition Letters . 27 (8): 861–874. doi :10.1016/j.patrec.2005.10.010. S2CID 2027090.
- ^ Провост, Фостер; Том Фосетт (2013-08-01). «Наука о данных для бизнеса: что вам нужно знать о добыче данных и аналитическом мышлении». O'Reilly Media, Inc.
- ^ Пауэрс, Дэвид МВ (2011). «Оценка: от точности, полноты и F-меры до ROC, информированности, маркированности и корреляции». Журнал технологий машинного обучения . 2 (1): 37–63.
- ^ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (ред.). Энциклопедия машинного обучения . Springer. doi :10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
- ^ Брукс, Гарольд; Браун, Барб; Эберт, Бет; Ферро, Крис; Джоллифф, Ян; Кох, Тие-Йонг; Рёббер, Пол; Стивенсон, Дэвид (2015-01-26). "WWRP/WGNE Joint Working Group on Forecast Verification Research". Collaboration for Australian Weather and Climate Research . World Meteorological Organization . Получено 17 июля 2019 г.
- ^ Chicco D, Jurman G (январь 2020 г.). «Преимущества коэффициента корреляции Мэтьюса (MCC) над оценкой F1 и точностью оценки бинарной классификации». BMC Genomics . 21 (1): 6-1–6-13. doi : 10.1186/s12864-019-6413-7 . PMC 6941312 . PMID 31898477.
- ^ Chicco D, Toetsch N, Jurman G (февраль 2021 г.). «Коэффициент корреляции Мэтьюса (MCC) более надежен, чем сбалансированная точность, информированность букмекера и маркированность при оценке двухклассовой матрицы путаницы». BioData Mining . 14 (13): 13. doi : 10.1186/s13040-021-00244-z . PMC 7863449 . PMID 33541410.
- ^ Tharwat A. (август 2018 г.). «Методы оценки классификации». Прикладная вычислительная техника и информатика . 17 : 168–192. doi : 10.1016/j.aci.2018.08.003 .
- ^ "классификация - AUC-ROC случайного классификатора". Data Science Stack Exchange . Получено 2020-11-30 .
- ^ abcd Чикко, Давиде; Юрман, Джузеппе (2023-02-17). «Коэффициент корреляции Мэтьюса (MCC) должен заменить ROC AUC в качестве стандартной метрики для оценки бинарной классификации». BioData Mining . 16 (1). Springer Science and Business Media LLC: 4. doi : 10.1186/s13040-023-00322-4 . hdl : 10281/430042 . ISSN 1756-0381. PMC 9938573. PMID 36800973 .
- ^ Muschelli, John (2019-12-23). «ROC и AUC с бинарным предиктором: потенциально вводящая в заблуждение метрика». Journal of Classification . 37 (3). Springer Science and Business Media LLC: 696–708. doi :10.1007/s00357-019-09345-1. ISSN 0176-4268. PMC 7695228 . PMID 33250548.
- ^ abc Лобо, Хорхе М.; Хименес-Вальверде, Альберто; Реал, Раймундо (2008). «AUC: вводящий в заблуждение показатель эффективности моделей прогнозируемого распределения». Глобальная экология и биогеография . 17 (2). Уайли: 145–151. дои : 10.1111/j.1466-8238.2007.00358.x. ISSN 1466-822X.
- ^ Халлиган, Стив; Альтман, Дуглас Г.; Маллетт, Сьюзан (2015-01-20). «Недостатки использования площади под кривой рабочей характеристики приемника для оценки тестов визуализации: обсуждение и предложение альтернативного подхода». Европейская радиология . 25 (4). Springer Science and Business Media LLC: 932–939. doi : 10.1007/s00330-014-3487-0 . ISSN 0938-7994. PMC 4356897. PMID 25599932 .
- ^ Беррар, Д.; Флах, П. (2011-03-21). «Предостережения и подводные камни анализа ROC в клинических исследованиях микрочипов (и как их избежать)». Briefings in Bioinformatics . 13 (1). Oxford University Press (OUP): 83–97. doi : 10.1093/bib/bbr008 . ISSN 1467-5463.
- ^ Ржезач, М., Ржезач, Ф. (2011). «Как измерить качество моделей кредитного скоринга». Чешский журнал экономики и финансов (Finance a úvěr) . 61 (5). Карлов университет Праги, факультет социальных наук: 486–507.
- ^ abc Powers, David MW (2012). "ROC-ConCert: Измерение согласованности и определенности на основе ROC" (PDF) . Весенний конгресс по инжинирингу и технологиям (SCET) . Том 2. IEEE. С. 238–241.[ мертвая ссылка ]
- ^ Фогарти, Джеймс; Бейкер, Райан С.; Хадсон, Скотт Э. (2005). «Исследования случаев использования анализа ROC-кривых для оценок на основе датчиков при взаимодействии человека с компьютером». Серия трудов Международной конференции ACM, Труды графического интерфейса 2005. Ватерлоо, Онтарио: Канадское общество по коммуникациям человека с компьютером.
- ^ Хасти, Тревор ; Тибширани, Роберт ; Фридман, Джером Х. (2009). Элементы статистического обучения: добыча данных, вывод и прогнозирование (2-е изд.).
- ^ Фосетт, Том (2006); Введение в анализ ROC , Pattern Recognition Letters, 27, 861–874.
- ^ Хэнли, Джеймс А.; Макнил, Барбара Дж. (1982). «Значение и использование площади под кривой рабочей характеристики приемника (ROC)». Радиология . 143 (1): 29–36. doi :10.1148/radiology.143.1.7063747. PMID 7063747. S2CID 10511727.
- ^ Мейсон, Саймон Дж.; Грэм, Николас Э. (2002). «Области под кривыми относительных рабочих характеристик (ROC) и относительных рабочих уровней (ROL): статистическая значимость и интерпретация» (PDF) . Quarterly Journal of the Royal Meteorological Society . 128 (584): 2145–2166. Bibcode :2002QJRMS.128.2145M. CiteSeerX 10.1.1.458.8392 . doi :10.1256/003590002320603584. S2CID 121841664. Архивировано из оригинала (PDF) 2008-11-20.
- ^ Колдерс, Мульт; Ярошевич, Шимон (2007). «Эффективная оптимизация AUC для классификации». В Коке, Йост Н.; Коронацкий, Яцек; Лопес де Мантарас, Рамон; Мэтвин, Стэн; Младенич, Дуня; Сковрон, Анджей (ред.). Обнаружение знаний в базах данных: PKDD 2007 . Конспекты лекций по информатике. Том. 4702. Берлин, Гейдельберг: Springer. стр. 42–53. дои : 10.1007/978-3-540-74976-9_8 . ISBN 978-3-540-74976-9.
- ^ Хэнд, Дэвид Дж. и Тилл, Роберт Дж. (2001); Простое обобщение площади под ROC-кривой для задач классификации нескольких классов , Машинное обучение, 45, 171–186.
- ^ Провост, Ф.; Фосетт, Т. (2001). «Надежная классификация для неточных сред». Машинное обучение . 42 (3): 203–231. arXiv : cs/0009007 . doi :10.1023/a:1007601015854. S2CID 5415722.
- ^ Флах, П. А.; Ву, С. (2005). «Исправление вогнутостей в кривых ROC». (PDF) . 19-я Международная объединенная конференция по искусственному интеллекту (IJCAI'05) . стр. 702–707.
- ^ Хэнли, Джеймс А.; Макнил, Барбара Дж. (1983-09-01). «Метод сравнения площадей под кривыми рабочих характеристик приемника, полученными из тех же случаев». Радиология . 148 (3): 839–843. doi : 10.1148/radiology.148.3.6878708 . PMID 6878708.
- ^ Ханчар, Блейз; Хуа, Цзяньпин; Сима, Чао; Вайнштейн, Джон; Биттнер, Майкл; Догерти, Эдвард Р. (2010). «Точность оценок, связанных с ROC, для малых выборок». Биоинформатика . 26 (6): 822–830. doi : 10.1093/bioinformatics/btq037 . PMID 20130029.
- ^ Лобо, Хорхе М.; Хименес-Вальверде, Альберто; Реал, Раймундо (2008). «AUC: вводящий в заблуждение показатель эффективности моделей прогнозируемого распределения». Глобальная экология и биогеография . 17 (2): 145–151. дои : 10.1111/j.1466-8238.2007.00358.x. S2CID 15206363.
- ^ Hand, David J (2009). «Измерение производительности классификатора: последовательная альтернатива площади под кривой ROC». Machine Learning . 77 : 103–123. doi : 10.1007/s10994-009-5119-5 . hdl : 10044/1/18420 .
- ^ Флах, П.А.; Эрнандес-Оралло, Дж.; Ферри, К. (2011). «Последовательная интерпретация AUC как меры совокупной эффективности классификации». (PDF) . Труды 28-й Международной конференции по машинному обучению (ICML-11) . стр. 657–664.
- ^ Эрнандес-Оралло, Дж.; Флах, П.А.; Ферри, К. (2012). «Единый взгляд на показатели производительности: перевод выбора порога в ожидаемую потерю классификации» (PDF) . Журнал исследований машинного обучения . 13 : 2813–2869.
- ^ Пауэрс, Дэвид М. В. (2012). «Проблема площади под кривой». Международная конференция по информационным наукам и технологиям .
- ^ Пауэрс, Дэвид МВ (2003). «Полнота и точность против букмекера» (PDF) . Труды Международной конференции по когнитивной науке (ICSC-2003), Сидней, Австралия, 2003, стр. 529–534 .
- ^ Powers, David MW (2012). "Проблема с Kappa" (PDF) . Конференция Европейского отделения Ассоциации компьютерной лингвистики (EACL2012) Совместный семинар ROBUS-UNSUP . Архивировано из оригинала (PDF) 2016-05-18 . Получено 2012-07-20 .
- ^ Макклиш, Донна Кацман (1989-08-01). «Анализ части кривой ROC». Принятие медицинских решений . 9 (3): 190–195. doi :10.1177/0272989X8900900307. PMID 2668680. S2CID 24442201.
- ^ Додд, Лори Э.; Пепе, Маргарет С. (2003). «Частичная оценка AUC и регрессия». Биометрия . 59 (3): 614–623. doi : 10.1111/1541-0420.00071 . PMID 14601762. S2CID 23054670.
- ^ Карплус, Кевин (2011); Лучше, чем случайность: важность нулевых моделей, Калифорнийский университет, Санта-Круз, в Трудах Первого международного семинара по распознаванию образов в протеомике, структурной биологии и биоинформатике (PR PS BB 2011)
- ^ "C-Statistic: Определение, Примеры, Взвешивание и Значимость". Statistics How To . 28 августа 2016 г.
- ^ Понтиус, Роберт Гилмор; Парментье, Бенуа (2014). «Рекомендации по использованию относительной эксплуатационной характеристики (ROC)». Landscape Ecology . 29 (3): 367–382. doi :10.1007/s10980-013-9984-8. S2CID 15924380.
- ^ Pontius, Robert Gilmore; Si, Kangping (2014). «Общая рабочая характеристика для измерения диагностической способности для нескольких порогов». Международный журнал географической информационной науки . 28 (3): 570–583. doi :10.1080/13658816.2013.862623. S2CID 29204880.
- ^ Navratil, J.; Klusacek, D. (2007-04-01). "О линейных DET". Международная конференция IEEE по акустике, речи и обработке сигналов 2007 года - ICASSP '07 . Том 4. стр. IV–229–IV–232. doi :10.1109/ICASSP.2007.367205. ISBN 978-1-4244-0727-9. S2CID 18173315.
- ^ Dev P. Chakraborty (14 декабря 2017 г.). "double+probability+paper"&pg=PT214 Методы оценки производительности наблюдателя для диагностической визуализации: основы, моделирование и приложения с примерами на основе R. CRC Press. стр. 214. ISBN 9781351230711. Получено 11 июля 2019 г. .
- ^ MacMillan, Neil A.; Creelman, C. Douglas (2005). Теория обнаружения: Руководство пользователя (2-е изд.). Mahwah, NJ: Lawrence Erlbaum Associates. ISBN 978-1-4106-1114-7.
- ^ Глэнзер, Мюррей; Кисок, Ким; Хилфорд, Энди; Адамс, Джон К. (1999). «Наклон характеристики работы приемника в памяти распознавания». Журнал экспериментальной психологии: обучение, память и познание . 25 (2): 500–513. doi :10.1037/0278-7393.25.2.500.
- ^ Ratcliff, Roger; McCoon, Gail; Tindall, Michael (1994). «Эмпирическая общность данных из функций ROC памяти распознавания и их значение для GMM». Журнал экспериментальной психологии: обучение, память и познание . 20 (4): 763–785. CiteSeerX 10.1.1.410.2114 . doi :10.1037/0278-7393.20.4.763. PMID 8064246.
- ^ Чжан, Цзюнь; Мюллер, Шейн Т. (2005). «Заметка об анализе ROC и непараметрической оценке чувствительности». Psychometrika . 70 : 203–212. CiteSeerX 10.1.1.162.1515 . doi :10.1007/s11336-003-1119-8. S2CID 122355230.
- ^ Йонелинас, Эндрю П.; Кролл, Нил EA; Доббинс, Ян Г.; Лаззара, Мишель; Найт, Роберт Т. (1998). «Дефицит воспоминаний и знакомства при амнезии: конвергенция данных «помнить-знать», диссоциации процессов и характеристик работы приемника». Нейропсихология . 12 (3): 323–339. doi :10.1037/0894-4105.12.3.323. PMID 9673991.
- ^ ab Грин, Дэвид М.; Суэтс, Джон А. (1966). Теория обнаружения сигналов и психофизика . Нью-Йорк, Нью-Йорк: John Wiley and Sons Inc. ISBN 978-0-471-32420-1.
- ^ "Использование кривой рабочей характеристики приемника (ROC) для анализа модели классификации: заключительная заметка исторического интереса" (PDF) . Кафедра математики, Университет Юты . Архивировано (PDF) из оригинала 2020-08-22 . Получено 25 мая 2017 г. .
- ^ Цвейг, Марк Х.; Кэмпбелл, Грегори (1993). «График ROC-характеристик приемника: фундаментальный инструмент оценки в клинической медицине» (PDF) . Клиническая химия . 39 (8): 561–577. doi : 10.1093/clinchem/39.4.561 . PMID 8472349.
- ^ Пепе, Маргарет С. (2003). Статистическая оценка медицинских тестов для классификации и прогнозирования . Нью-Йорк, Нью-Йорк: Оксфорд. ISBN 978-0-19-856582-6.
- ^ Обуховски, Нэнси А. (2003). «Кривые рабочих характеристик приемника и их использование в радиологии». Радиология . 229 (1): 3–8. doi :10.1148/radiol.2291010898. PMID 14519861.
- ^ Спэкман, Кент А. (1989). «Теория обнаружения сигналов: ценные инструменты для оценки индуктивного обучения». Труды Шестого международного семинара по машинному обучению . Сан-Матео, Калифорния: Morgan Kaufmann . С. 160–163.
- ^ Харин, Вячеслав (2003). «О шкале ROC вероятностных прогнозов». Журнал климата . 16 (24): 4145–4150. Bibcode :2003JCli...16.4145K. doi : 10.1175/1520-0442(2003)016<4145:OTRSOP>2.0.CO;2 .
- ^ "Основы радиолокации", Методы цифровой обработки сигналов и их применение в обработке радиолокационных изображений , Хобокен, Нью-Джерси, США: John Wiley & Sons, Inc., стр. 93–115, 29.01.2008, doi :10.1002/9780470377765.ch4, ISBN 9780470377765, получено 2023-05-20
- ^ Тилл, DJ; Хэнд, RJ (2001). «Простое обобщение площади под кривой ROC для задач классификации нескольких классов». Машинное обучение . 45 (2): 171–186. doi : 10.1023/A:1010920819831 .
- ^ Моссман, Д. (1999). «Трехсторонние ROC». Принятие медицинских решений . 19 (1): 78–89. doi :10.1177/0272989x9901900110. PMID 9917023. S2CID 24623127.
- ^ Ферри, К.; Эрнандес-Оралло, Дж.; Салидо, М.А. (2003). «Объем под поверхностью ROC для многоклассовых задач». Машинное обучение: ECML 2003. С. 108–120.
- ^ Би, Дж.; Беннетт, К. П. (2003). "Характерные кривые ошибок регрессии" (PDF) . Двадцатая международная конференция по машинному обучению (ICML-2003). Вашингтон, округ Колумбия .
- ^ Hernandez-Orallo, J. (2013). "ROC-кривые для регрессии". Pattern Recognition . 46 (12): 3395–3411. Bibcode : 2013PatRe..46.3395H. doi : 10.1016/j.patcog.2013.06.014. hdl : 10251/40252 . S2CID 15651724.
Внешние ссылки
- простой калькулятор ROC
- Анимированная демонстрация ROC
- демонстрация РОЦ
- еще одна демонстрация ROC
- Видео-объяснение ROC
- Введение в общую эксплуатационную характеристику: оценка полезности в модели изменения земельных ресурсов
- Как запустить пакет TOC в R
- Пакет TOC R на Github
- Рабочая книга Excel для создания кривых TOC
Дальнейшее чтение
- Балакришнан, Нараянасвами (1991); Справочник по логистическому распределению , Marcel Dekker, Inc., ISBN 978-0-8247-8587-1
- Браун, Кристофер Д.; Дэвис, Герберт Т. (2006). «Кривые рабочих характеристик приемника и связанные с ними меры принятия решений: учебное пособие». Хемометрика и интеллектуальные лабораторные системы . 80 : 24–38. doi :10.1016/j.chemolab.2005.05.004.
- Ротелло, Карен М.; Хейт, Эван; Дубе, Чад (2014). «Когда больше данных сбивают нас с толку: репликации с неправильной зависимой мерой увековечивают ошибочные выводы» (PDF) . Psychonomic Bulletin & Review . 22 (4): 944–954. doi : 10.3758/s13423-014-0759-2 . PMID 25384892. S2CID 6046065.
- Fawcett, Tom (2004). "Графики ROC: заметки и практические соображения для исследователей" (PDF) . Pattern Recognition Letters . 27 (8): 882–891. CiteSeerX 10.1.1.145.4649 . doi :10.1016/j.patrec.2005.10.012.
- Гонен, Митхат (2007); Анализ кривых рабочих характеристик приемника с использованием SAS , SAS Press, ISBN 978-1-59994-298-8
- Грин, Уильям Х., (2003) Эконометрический анализ , пятое издание, Prentice Hall , ISBN 0-13-066189-9
- Хегерти, Патрик Дж.; Ламли, Томас; Пепе, Маргарет С. (2000). «Зависящие от времени ROC-кривые для цензурированных данных о выживании и диагностический маркер». Биометрия . 56 (2): 337–344. doi :10.1111/j.0006-341x.2000.00337.x. PMID 10877287. S2CID 8822160.
- Хосмер, Дэвид У.; и Лемешоу, Стэнли (2000); Прикладная логистическая регрессия , 2-е изд., Нью-Йорк, штат Нью-Йорк: Wiley , ISBN 0-471-35632-8
- Ласко, Томас А.; Бхагват, Джуи Г.; Зоу, Келли Х.; Оно-Мачадо, Люсила (2005). «Использование кривых рабочих характеристик приемника в биомедицинской информатике». Журнал биомедицинской информатики . 38 (5): 404–415. CiteSeerX 10.1.1.97.9674 . doi :10.1016/j.jbi.2005.02.008. PMID 16198999.
- Мас, Жан-Франсуа; Фильо, Бритальдо Соарес; Понтиус-младший, Роберт Гилмор; Гутьеррес, Мишель Фарфан; Родригес, Герман (2013). «Набор инструментов для ROC-анализа пространственных моделей». Международный журнал геоинформации ISPRS . 2 (3): 869–887. Бибкод : 2013IJGI....2..869M. дои : 10.3390/ijgi2030869 .
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Понтиус, младший, Роберт Гилмор; Парментье, Бенуа (2014). «Рекомендации по использованию относительной эксплуатационной характеристики (ROC)». Landscape Ecology . 29 (3): 367–382. doi :10.1007/s10980-013-9984-8. S2CID 15924380.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Понтиус, младший, Роберт Гилмор; Пачеко, Пабло (2004). «Калибровка и проверка модели нарушения лесов в Западных Гатах, Индия, 1920–1990». GeoJournal . 61 (4): 325–334. doi :10.1007/s10708-004-5049-5. S2CID 155073463.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Pontius, Jr, Robert Gilmore; Batchu, Kiran (2003). «Использование относительной рабочей характеристики для количественной оценки уверенности в прогнозировании местоположения изменения земельного покрова в Индии». Transactions in GIS . 7 (4): 467–484. doi :10.1111/1467-9671.00159. S2CID 14452746.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Pontius, Jr, Robert Gilmore; Schneider, Laura (2001). «Проверка модели изменения землепользования методом ROC для водораздела Ипсвича, Массачусетс, США». Agriculture, Ecosystems & Environment . 85 (1–3): 239–248. doi :10.1016/S0167-8809(01)00187-6.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Стефан, Карстен; Весселинг, Себастьян; Шинк, Таня; Юнг, Клаус (2003). «Сравнение восьми компьютерных программ для анализа характеристик работы приемника». Клиническая химия . 49 (3): 433–439. doi : 10.1373/49.3.433 . PMID 12600955.
- Swets, Джон А.; Dawes, Робин М.; и Monahan, Джон (2000); Лучшие решения с помощью науки , Scientific American , октябрь, стр. 82–87
- Zou, Kelly H.; O'Malley, A. James; Mauri, Laura (2007). «Анализ характеристик работы приемника для оценки диагностических тестов и прогностических моделей». Circulation . 115 (5): 654–7. doi : 10.1161/circulationaha.105.594929 . PMID 17283280.
- Чжоу, Сяо-Хуа; Обуховски, Нэнси А .; Макклиш, Донна К. (2002). Статистические методы в диагностической медицине . Нью-Йорк, Нью-Йорк: Wiley & Sons. ISBN 978-0-471-34772-9.
- Chicco D.; Jurman G. (2023). «Коэффициент корреляции Мэтьюза (MCC) должен заменить ROC AUC в качестве стандартной метрики для оценки бинарной классификации». BioData Mining . 16 (1): 4. doi : 10.1186/s13040-023-00322-4 . PMC 9938573 . PMID 36800973.














![{\displaystyle {\begin{aligned}A&=\int _{x=0}^{1}{\mbox{TPR}}({\mbox{FPR}}^{-1}(x))\,dx\\[5pt]&=\int _{\infty }^{-\infty }{\mbox{TPR}}(T){\mbox{FPR}}'(T)\,dT\\[5pt]&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }I(T'\geq T)f_{1}(T')f_{0}(T)\,dT'\,dT=P(X_{1}\geq X_{0})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdb0372c3b4aa60b02b19360ef1fbf8ddd8d221e)






![{\displaystyle {\text{AUC}}(f)={\frac {\sum _{t_{0}\in {\mathcal {D}}^{0}}\sum _{t_{1}\in {\mathcal {D}}^{1}}{\textbf {1}}[f(t_{0})<f(t_{1})]}{|{\mathcal {D}}^{0} |\cdot |{\mathcal {D}}^{1}|}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ad12d9aef8c040aea59bc20304b821fc9b99232)
![{\textstyle {\textbf {1}}[f(t_{0})<f(t_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03407a2c3018d99fb12703e2327bfbf84b9ce426)













