Реконструкция предков
Реконструкция предков (также известная как картирование признаков или оптимизация признаков ) — это экстраполяция назад во времени измеренных характеристик особей, популяций или видов к их общим предкам . Это важное приложение филогенетики , реконструкция и изучение эволюционных отношений между особями, популяциями или видами к их предкам. В контексте эволюционной биологии реконструкция предков может использоваться для восстановления различных видов состояний предковых признаков организмов, которые жили миллионы лет назад. [1] Эти состояния включают генетическую последовательность ( реконструкция предковой последовательности ), аминокислотную последовательность белка , состав генома ( например, порядок генов), измеримую характеристику организма ( фенотип ) и географический ареал предковой популяции или вида (реконструкция ареала предков). Это желательно, поскольку позволяет нам исследовать части филогенетических деревьев, соответствующие далекому прошлому, проясняя эволюционную историю вида в дереве. Поскольку современные генетические последовательности по сути являются вариацией древних, доступ к древним последовательностям может идентифицировать другие вариации и организмы, которые могли возникнуть из этих последовательностей. [2] В дополнение к генетическим последовательностям можно попытаться отследить изменение одной черты характера на другую, например, превращение плавников в ноги.
Небиологические приложения включают реконструкцию словарного запаса или фонем древних языков [3] и культурных особенностей древних обществ, таких как устные традиции [4] или брачные практики [5] .
Реконструкция предков опирается на достаточно реалистичную статистическую модель эволюции для точного восстановления предковых состояний. Эти модели используют генетическую информацию, уже полученную с помощью таких методов, как филогенетика, для определения пути, по которому пошла эволюция , и времени, когда произошли эволюционные события. [6] Однако независимо от того, насколько хорошо модель аппроксимирует фактическую эволюционную историю, способность точно реконструировать предка ухудшается с увеличением эволюционного времени между этим предком и его наблюдаемыми потомками. Кроме того, более реалистичные модели эволюции неизбежно более сложны и трудны для расчета. Прогресс в области реконструкции предков в значительной степени опирался на экспоненциальный рост вычислительной мощности и сопутствующую разработку эффективных вычислительных алгоритмов (например, алгоритм динамического программирования для совместной реконструкции максимального правдоподобия предковых последовательностей). [7] Методы реконструкции предков часто применяются к данному филогенетическому дереву , которое уже было выведено из тех же данных. Несмотря на удобство, этот подход имеет тот недостаток, что его результаты зависят от точности одного филогенетического дерева. Напротив, некоторые исследователи [8] выступают за более интенсивный в плане вычислений байесовский подход, который учитывает неопределенность в реконструкции деревьев путем оценки предковых реконструкций по многим деревьям.
История
Концепция предковой реконструкции часто приписывается Эмилю Цукеркандлю и Линусу Полингу . Мотивированные разработкой методов определения первичной (аминокислотной) последовательности белков Фредериком Сэнгером в 1955 году [9], Цукеркандль и Полинг постулировали [10] , что такие последовательности могут быть использованы для вывода не только филогении, связывающей наблюдаемые белковые последовательности, но и предковой белковой последовательности в самой ранней точке (корне) этого дерева. Однако идея реконструкции предков по измеримым биологическим характеристикам уже развивалась в области кладистики , одного из предшественников современной филогенетики. Кладистические методы, которые появились еще в 1901 году, выводят эволюционные связи видов на основе распределения общих характеристик, некоторые из которых, как предполагается, произошли от общих предков. Кроме того, в 1938 году Феодосий Добжанский и Альфред Стертевант сформулировали принципы реконструкции предков в филогенетическом контексте, делая выводы об эволюционной истории хромосомных инверсий у Drosophila pseudoobscura . [11]
Таким образом, предковая реконструкция имеет свои корни в нескольких дисциплинах. Сегодня вычислительные методы для предковой реконструкции продолжают расширяться и применяться в различных условиях, так что предковые состояния выводятся не только для биологических характеристик и молекулярных последовательностей, но также для структуры [12] [13] или каталитических свойств [14] древних и современных белков , географического расположения популяций и видов ( филогеография ) [15] [16] и структуры геномов более высокого порядка. [17]
Методы и алгоритмы
Любая попытка реконструкции предков начинается с филогении . В общем, филогения — это основанная на дереве гипотеза о порядке, в котором популяции (называемые таксонами ) связаны происхождением от общих предков. Наблюдаемые таксоны представлены вершинами или конечными узлами дерева, которые постепенно соединяются ветвями со своими общими предками, которые представлены точками ветвления дерева, которые обычно называются предковыми или внутренними узлами . В конечном итоге все родословные сходятся к самому последнему общему предку всей выборки таксонов. В контексте реконструкции предков филогения часто рассматривается так, как если бы она была известной величиной (за исключением байесовских подходов). Поскольку может быть огромное количество филогений, которые почти одинаково эффективны для объяснения данных, сокращение подмножества филогений, поддерживаемых данными, до одного представителя или точечной оценки может быть удобным и иногда необходимым упрощающим предположением.
Реконструкцию предков можно рассматривать как прямой результат применения гипотетической модели эволюции к данной филогении. Когда модель содержит один или несколько свободных параметров, общая цель состоит в оценке этих параметров на основе измеренных характеристик среди наблюдаемых таксонов (последовательностей), которые произошли от общих предков. Экономия является важным исключением из этой парадигмы: хотя было показано, что существуют обстоятельства, при которых она является оценщиком максимального правдоподобия [18] , по своей сути она просто основана на эвристике, что изменения в состоянии признака редки, без попытки количественно оценить эту редкость.
Существует три различных класса методов для реконструкции предков. В хронологическом порядке открытия это максимальная экономия , максимальное правдоподобие и байесовский вывод . Максимальная экономия считает все эволюционные события одинаково вероятными; максимальное правдоподобие учитывает различную вероятность определенных классов событий; а байесовский вывод связывает условную вероятность события с вероятностью дерева, а также с величиной неопределенности, связанной с этим деревом. Максимальная экономия и максимальное правдоподобие дают один наиболее вероятный результат, тогда как байесовский вывод учитывает неопределенности в данных и дает выборку возможных деревьев.
Максимальная бережливость
Экономия, в просторечии известная как « бритва Оккама », относится к принципу выбора простейшей из конкурирующих гипотез. В контексте реконструкции предков экономия стремится найти распределение предковых состояний в пределах данного дерева, которое минимизирует общее количество изменений состояний признаков, которые были бы необходимы для объяснения состояний, наблюдаемых на вершинах дерева. Этот метод максимальной экономии [19] является одним из самых ранних формализованных алгоритмов для реконструкции предковых состояний, а также одним из самых простых. [13]
Максимальная экономия может быть реализована одним из нескольких алгоритмов. Одним из самых ранних примеров является метод Фитча [20] , который назначает состояния предкового символа с помощью экономии посредством двух обходов корневого двоичного дерева . Первый этап - это обход в обратном порядке , который идет от кончиков к корню дерева, посещая узлы-потомки (дочерние) до их родителей. Первоначально мы определяем множество возможных состояний символа S i для i -го предка на основе наблюдаемых состояний символа его потомков. Каждое назначение - это множество пересечений состояний символа потомков предка; если пересечение - это пустое множество, то это объединение множеств . В последнем случае подразумевается, что изменение состояния символа произошло между предком и одним из его двух непосредственных потомков. Каждое такое событие учитывается в функции стоимости алгоритма, которая может использоваться для различения альтернативных деревьев на основе максимальной экономии. Затем выполняется предварительный обход дерева, начиная с корня к кончикам. Затем состояния символов назначаются каждому потомку на основе того, какие состояния символов он разделяет со своим родителем. Поскольку у корня нет родительского узла, может потребоваться выбрать состояние символа произвольно, особенно когда в корне реконструировано более одного возможного состояния.

Например, рассмотрим филогению, восстановленную для рода растений, содержащего 6 видов A - F, где каждое растение опыляется либо «пчелой», либо «колибри», либо «ветром». Один очевидный вопрос заключается в том, какие опылители в более глубоких узлах были в филогении этого рода растений. При максимальной экономии реконструкция предкового состояния для этой клады показывает, что «колибри» является наиболее экономным предковым состоянием для нижней клады (растения D, E, F), что предковые состояния для узлов в верхней кладе (растения A, B, C) неоднозначны и что как «колибри», так и «пчела» опылители одинаково правдоподобны для состояния опыления в корне филогении. Предположим, у нас есть веские доказательства из ископаемой летописи, что корневое состояние — «колибри». Разрешение корня до «колибри» даст модель реконструкции предкового состояния, изображенную символами в узлах, при этом состояние, требующее наименьших изменений, обведено кружком.
Методы экономии интуитивно привлекательны и высокоэффективны, поэтому они все еще используются в некоторых случаях для затравки алгоритмов оптимизации максимального правдоподобия с начальной филогенией. [21] Однако базовое предположение о том, что эволюция достигла определенного конечного результата как можно быстрее, неверно. Естественный отбор и эволюция не работают на достижение цели, они просто выбирают за или против случайно происходящих генетических изменений. Методы экономии предполагают шесть общих предположений: что используемое вами филогенетическое дерево является правильным, что у вас есть все соответствующие данные, в которых не было сделано ошибок при кодировании, что все ветви филогенетического дерева с равной вероятностью изменятся, что скорость эволюции медленная и что вероятность потери или приобретения характеристики одинакова. [1] В действительности предположения часто нарушаются, что приводит к нескольким проблемам:
- Изменение в скорости эволюции. Метод Фитча предполагает, что изменения между всеми состояниями характера происходят с одинаковой вероятностью; таким образом, любое изменение влечет за собой одинаковые затраты для данного дерева. Это предположение часто нереалистично и может ограничивать точность таких методов. [8] Например, переходы , как правило, происходят чаще, чем трансверсии в эволюции нуклеиновых кислот. Это предположение можно ослабить, назначив дифференциальные затраты конкретным изменениям состояний характера, что приведет к взвешенному алгоритму экономии. [22]
- Быстрая эволюция. Результат эвристики «минимальной эволюции», лежащей в основе таких методов, заключается в том, что такие методы предполагают, что изменения редки , и, таким образом, не подходят в случаях, когда изменение является нормой, а не исключением. [23] [24]
- Различия во времени между родословными. Методы экономии неявно предполагают, что одинаковое количество эволюционного времени прошло по каждой ветви дерева. Таким образом, они не учитывают различия в длине ветвей в дереве, которые часто используются для количественной оценки прохождения эволюционного или хронологического времени. Это ограничение делает метод склонным делать вывод, что одно изменение произошло на очень короткой ветви, а не несколько изменений, происходящих на очень длинной ветви, например. [25] Кроме того, возможно, что некоторые ветви дерева могут испытывать более высокие скорости отбора и изменения, чем другие, возможно, из-за изменения факторов окружающей среды. Некоторые периоды времени могут представлять более быструю эволюцию, чем другие, когда это происходит, экономия становится неточной. [26] Этот недостаток устраняется методами, основанными на моделях (как методами максимального правдоподобия, так и байесовскими методами), которые выводят стохастический процесс эволюции по мере его развертывания вдоль каждой ветви дерева. [27]
- Статистическое обоснование. Без статистической модели, лежащей в основе метода, его оценки не имеют четко определенных неопределенностей. [23] [25] [28]
- Конвергентная эволюция. При рассмотрении одного состояния признака экономия автоматически предполагает, что два организма, которые разделяют эту характеристику, будут более тесно связаны, чем те, которые ее не разделяют. Например, то, что у собак и обезьян есть шерсть, не означает, что они более тесно связаны, чем обезьяны с людьми.
Максимальная вероятность
Методы максимального правдоподобия (ML) реконструкции предкового состояния рассматривают состояния признаков во внутренних узлах дерева как параметры и пытаются найти значения параметров, которые максимизируют вероятность данных (наблюдаемых состояний признаков) с учетом гипотезы (модели эволюции и филогении, связывающей наблюдаемые последовательности или таксоны). Другими словами, этот метод предполагает, что предковые состояния являются теми, которые статистически наиболее вероятны, учитывая наблюдаемые фенотипы. Некоторые из самых ранних подходов ML к реконструкции предков были разработаны в контексте эволюции генетической последовательности ; [29] [30] аналогичные модели были также разработаны для аналогичного случая дискретной эволюции признаков. [31]
Использование модели эволюции учитывает тот факт, что не все события имеют одинаковую вероятность. Например, переход , который является типом точечной мутации от одного пурина к другому или от одного пиримидина к другому, имеет гораздо большую вероятность, чем трансверсия , которая является вероятностью переключения пурина на пиримидин или наоборот. Эти различия не охватываются максимальной экономией. Однако то, что некоторые события более вероятны, чем другие, не означает, что они всегда происходят. Мы знаем, что на протяжении всей эволюционной истории были времена, когда существовал большой разрыв между тем, что с наибольшей вероятностью произойдет, и тем, что произошло на самом деле. Когда это так, максимальная экономия может быть на самом деле более точной, поскольку она более склонна совершать большие, маловероятные скачки, чем максимальная вероятность. Было показано, что максимальная вероятность довольно надежна при реконструкции состояний признаков, но она не так хороша для точной оценки стабильности белков. Максимальное правдоподобие всегда переоценивает стабильность белков, что имеет смысл, поскольку предполагает, что белки, которые были созданы и использованы, были наиболее стабильными и оптимальными. [13] Достоинства максимального правдоподобия были предметом споров, и некоторые пришли к выводу, что тест максимального правдоподобия представляет собой хорошую середину между точностью и скоростью. [32] Однако другие исследования жаловались, что максимальное правдоподобие требует слишком много времени и вычислительной мощности, чтобы быть полезным в некоторых сценариях. [33]
Эти подходы используют ту же вероятностную структуру, которая использовалась для вывода филогенетического дерева. [34] Вкратце, эволюция генетической последовательности моделируется обратимым во времени непрерывным марковским процессом . В простейшем из них все признаки претерпевают независимые переходы состояний (такие как замены нуклеотидов) с постоянной скоростью с течением времени. Эта базовая модель часто расширяется, чтобы допускать различные скорости на каждой ветви дерева. В действительности скорости мутаций также могут меняться со временем (например, из-за изменений окружающей среды); это можно смоделировать, позволяя параметрам скорости эволюционировать вдоль дерева за счет увеличения числа параметров. Модель определяет вероятности перехода из состояний i в j вдоль ветви длиной t (в единицах эволюционного времени). Вероятность филогении вычисляется из вложенной суммы вероятностей перехода, которая соответствует иерархической структуре предлагаемого дерева. В каждом узле вероятность его потомков суммируется по всем возможным состояниям предковых признаков в этом узле:
где мы вычисляем вероятность поддерева с корнем в узле x с прямыми потомками y и z , обозначает состояние символа i -го узла, — длина ветви (эволюционное время) между узлами i и j , а — набор всех возможных состояний символа (например, нуклеотиды A, C, G и T). [34] Таким образом, цель реконструкции предков — найти назначение для всех x внутренних узлов, которое максимизирует вероятность наблюдаемых данных для данного дерева.
Предельная и совместная вероятность
Вместо вычисления общей вероятности для альтернативных деревьев, проблема реконструкции предков заключается в поиске комбинации состояний характера в каждом узле предка с наивысшим предельным максимальным правдоподобием. Вообще говоря, есть два подхода к этой проблеме. Во-первых, можно назначить наиболее вероятное состояние характера каждому предку независимо от реконструкции всех других состояний предка. Этот подход называется предельной реконструкцией . Он похож на суммирование по всем комбинациям состояний предка во всех других узлах дерева (включая корневой узел), кроме тех, для которых доступны данные. Предельная реконструкция — это нахождение состояния в текущем узле, которое максимизирует вероятность, интегрированную по всем другим состояниям во всех узлах, пропорционально их вероятности. Во-вторых, вместо этого можно попытаться найти совместную комбинацию состояний характера предка по всему дереву, которая совместно максимизирует вероятность всего набора данных. Таким образом, этот подход называется совместной реконструкцией. [29] Неудивительно, что совместная реконструкция является более сложной в вычислительном отношении, чем предельная реконструкция. Тем не менее, были разработаны эффективные алгоритмы для совместной реконструкции, временная сложность которых, как правило, линейно зависит от числа наблюдаемых таксонов или последовательностей. [7]
Методы реконструкции предков на основе МО, как правило, обеспечивают большую точность, чем методы МП, при наличии вариаций в скоростях эволюции среди признаков (или между участками в геноме). [35] [36] Однако эти методы пока не способны учитывать вариации в скоростях эволюции с течением времени, иначе известные как гетеротахия . Если скорость эволюции для определенного признака ускоряется на ветви филогении, то количество эволюции, произошедшей на этой ветви, будет недооценено для данной длины ветви и при условии постоянной скорости эволюции для этого признака. В дополнение к этому, трудно отличить гетеротахию от вариаций среди признаков в скоростях эволюции. [37]
Поскольку ML (в отличие от максимальной экономии) требует от исследователя указания модели эволюции, на его точность может повлиять использование грубо неверной модели (неправильная спецификация модели). Кроме того, ML может обеспечить только однократную реконструкцию состояний характера (что часто называют «точечной оценкой») — когда поверхность правдоподобия сильно невыпуклая, включающая несколько пиков (локальные оптимумы), то однократная точечная оценка не может обеспечить адекватное представление, и байесовский подход может быть более подходящим.
Байесовский вывод
Байесовский вывод использует вероятность наблюдаемых данных для обновления убеждения исследователя или априорного распределения , чтобы получить апостериорное распределение . В контексте реконструкции предков цель состоит в том, чтобы вывести апостериорные вероятности состояний предковых признаков в каждом внутреннем узле данного дерева. Более того, можно интегрировать эти вероятности по апостериорным распределениям по параметрам эволюционной модели и пространству всех возможных деревьев. Это можно выразить как применение теоремы Байеса :
где S представляет собой предковые состояния, D соответствует наблюдаемым данным и представляет как эволюционную модель, так и филогенетическое дерево. — это вероятность наблюдаемых данных, которая может быть вычислена с помощью алгоритма обрезки Фельзенштейна , как указано выше. — это априорная вероятность предковых состояний для данной модели и дерева. Наконец, — это вероятность данных для данной модели и дерева, интегрированная по всем возможным предковым состояниям.
Байесовский вывод — это метод, который многие считают наиболее точным. [8] В целом, байесовский статистический метод позволяет исследователям объединять уже существующую информацию с новой гипотезой. В случае эволюции он объединяет вероятность наблюдаемых данных с вероятностью того, что события произошли в том порядке, в котором они произошли, признавая при этом потенциальную возможность ошибки и неопределенности. В целом, это наиболее точный метод реконструкции предковых генетических последовательностей, а также стабильности белка. [25] В отличие от двух других методов, байесовский вывод дает распределение возможных деревьев, что позволяет получать более точные и легко интерпретируемые оценки дисперсии возможных результатов. [38]
Выше мы привели две формулировки, чтобы подчеркнуть два различных применения теоремы Байеса, которые мы обсудим в следующем разделе.
Эмпирический и иерархический Байес
Одна из первых реализаций байесовского подхода к реконструкции наследственной последовательности была разработана Янгом и коллегами [29] , где оценки максимального правдоподобия эволюционной модели и дерева, соответственно, использовались для определения априорных распределений. Таким образом, их подход является примером эмпирического байесовского метода для вычисления апостериорных вероятностей состояний предковых признаков; этот метод был впервые реализован в программном пакете PAML. [39] В терминах приведенной выше формулировки байесовского правила эмпирический байесовский метод фиксируется на эмпирических оценках модели и дерева, полученных из данных, эффективно отбрасывая апостериорное правдоподобие и априорные члены формулы. Более того, Янг и коллеги [29] использовали эмпирическое распределение шаблонов сайтов (т. е. назначения нуклеотидов вершинам дерева) при выравнивании наблюдаемых нуклеотидных последовательностей в знаменателе вместо исчерпывающего вычисления по всем возможным значениям S при заданном . С вычислительной точки зрения эмпирический метод Байеса похож на реконструкцию предковых состояний по методу максимального правдоподобия, за исключением того, что вместо поиска назначений состояний методом машинного обучения на основе их соответствующих распределений вероятностей в каждом внутреннем узле, сами распределения вероятностей сообщаются напрямую.
Эмпирические байесовские методы для реконструкции предков требуют от исследователя предположить, что параметры эволюционной модели и дерево известны без ошибок. Когда размер или сложность данных делают это предположение нереалистичным, может быть более благоразумным принять полностью иерархический байесовский подход и вывести совместное апостериорное распределение по состояниям предковых признаков, модели и дереву. [40] Хюльзенбек и Боллбак впервые предложили [40] иерархический байесовский метод для реконструкции предков с использованием методов Монте-Карло с цепями Маркова (MCMC) для выборки последовательностей предков из этого совместного апостериорного распределения. Похожий подход также использовался для реконструкции эволюции симбиоза с водорослями у видов грибов ( лихенизация ). [41] Например, алгоритм Метрополиса-Гастингса для MCMC исследует совместное апостериорное распределение, принимая или отклоняя назначения параметров на основе отношения апостериорных вероятностей.
Проще говоря, эмпирический байесовский подход вычисляет вероятности различных предковых состояний для конкретного дерева и модели эволюции. Выражая реконструкцию предковых состояний как набор вероятностей, можно напрямую количественно оценить неопределенность для назначения любого конкретного состояния предку. С другой стороны, иерархический байесовский подход усредняет эти вероятности по всем возможным деревьям и моделям эволюции пропорционально тому, насколько вероятны эти деревья и модели, учитывая данные, которые были получены.
Однако вопрос о том, дает ли иерархический байесовский метод существенное преимущество на практике, остается спорным. [42] Более того, этот полностью байесовский подход ограничен анализом относительно небольшого количества последовательностей или таксонов, поскольку пространство всех возможных деревьев быстро становится слишком обширным, что делает вычислительно невозможным схождение цепных выборок за разумное время.
Калибровка
Реконструкция предков может быть основана на наблюдаемых состояниях в исторических образцах известного возраста, таких как ископаемые останки или архивные образцы. Поскольку точность реконструкции предков обычно снижается со временем, использование таких образцов дает данные, которые ближе к реконструируемым предкам и, скорее всего, улучшит анализ, особенно когда скорости изменения признаков меняются со временем. Эта концепция была подтверждена экспериментальным эволюционным исследованием, в котором репликативные популяции бактериофага T7 были размножены для создания искусственной филогении. [43] Пересматривая эти экспериментальные данные, Окли и Каннингем [44] обнаружили, что методы максимальной экономии не смогли точно реконструировать известное состояние предков непрерывного признака ( размер бляшки ); эти результаты были подтверждены компьютерным моделированием. Эта неудача реконструкции предков была приписана направленному смещению в эволюции размера бляшки (от больших к малым диаметрам бляшки), что потребовало включения «окаменелых» образцов для решения.
Исследования как млекопитающих плотоядных [45], так и рыб [46] продемонстрировали, что без включения ископаемых данных реконструированные оценки размеров тела предков нереалистично велики. Более того, Грэм Слейтер и коллеги показали [47] с использованием собачьих плотоядных , что включение ископаемых данных в априорные распределения улучшило как байесовский вывод предковых состояний, так и выбор эволюционной модели по сравнению с анализами, использующими только современные данные.
Модели
Было разработано много моделей для оценки предковых состояний дискретных и непрерывных признаков из существующих потомков. [48] Такие модели предполагают, что эволюция признака с течением времени может быть смоделирована как стохастический процесс. Для дискретно-значимых признаков (таких как «тип опылителя») этот процесс обычно принимается за цепь Маркова ; для непрерывно-значимых признаков (таких как « размер мозга ») процесс часто принимается за броуновское движение или процесс Орнштейна-Уленбека . Используя эту модель в качестве основы для статистического вывода, теперь можно использовать методы максимального правдоподобия или байесовский вывод для оценки предковых состояний.
Модели с дискретными состояниями
Предположим, что рассматриваемый признак может попасть в одно из состояний, обозначенных . Типичным средством моделирования эволюции этого признака является непрерывная во времени цепь Маркова, которую можно кратко описать следующим образом. Каждое состояние имеет связанные с ним скорости перехода во все другие состояния. Признак моделируется как шагающий между состояниями ; когда он достигает заданного состояния, он запускает экспоненциальные «часы» для каждого из других состояний, в которые он может перейти. Затем он «гоняет» часы друг с другом и делает шаг к состоянию, часы которого зазвонят первыми. В такой модели параметрами являются скорости перехода , которые можно оценить, используя, например, методы максимального правдоподобия, где максимизируется по набору всех возможных конфигураций состояний предковых узлов.

Чтобы восстановить состояние заданного предкового узла в филогении (назовем этот узел ) по максимальному правдоподобию, процедура такова: найти оценку максимального правдоподобия ; затем вычислить правдоподобие каждого возможного состояния для обусловливания ; наконец, выбрать предковое состояние, которое максимизирует это. [23] Можно также использовать эту модель подстановки в качестве основы для процедуры байесовского вывода, которая будет учитывать апостериорное убеждение в состоянии предкового узла с учетом некоторого выбранного пользователем априорного значения.
Поскольку такие модели могут иметь столько же параметров, переобучение может быть проблемой. Некоторые распространенные варианты, которые уменьшают пространство параметров:
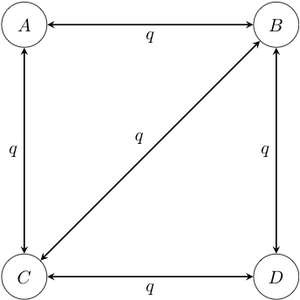
- Модель Markov -state 1 Parameter : эта модель является обратным во времени -state аналогом модели Jukes-Cantor . В этой модели все переходы имеют одинаковую скорость , независимо от их начального и конечного состояний. Некоторые переходы могут быть запрещены путем объявления их скоростей просто равными 0; это может быть так, например, если определенные состояния не могут быть достигнуты из других состояний за один переход.

Пример модели цепи Маркова с четырьмя состояниями и одним параметром. Обратите внимание, что на этой диаграмме переходы между состояниями A и D запрещены; принято не рисовать стрелку, а рисовать ее со скоростью 0. - Асимметричная марковская модель с 2 параметрами состояния : в этой модели пространство состояний упорядочено (так что, например, состояние 1 меньше состояния 2, которое меньше состояния 3), и переходы могут происходить только между соседними состояниями. Эта модель содержит два параметра и : один для скорости увеличения состояния (например, от 0 до 1, от 1 до 2 и т. д.), а другой для скорости уменьшения состояния (например, от 2 до 1, от 1 до 0 и т. д.).

Графическое представление асимметричной пятиуровневой двухпараметрической модели цепи Маркова.
Пример: модель видообразования и вымирания в бинарном состоянии
Модель бинарного состояния видообразования и вымирания [49] (BiSSE) — это дискретно-пространственная модель, которая напрямую не следует структуре упомянутых выше. Она позволяет оценивать предковые бинарные состояния признаков совместно с показателями диверсификации , связанными с различными состояниями признаков; ее также можно напрямую расширить до более общей модели с несколькими дискретными состояниями. В своей самой базовой форме эта модель включает шесть параметров: два показателя видообразования (по одному для линий в состояниях 0 и 1); аналогично, два показателя вымирания; и два показателя изменения признаков. Эта модель позволяет проверять гипотезы о показателях видообразования/вымирания/изменения признаков за счет увеличения числа параметров.
Модели непрерывного состояния
В случае, когда признак принимает недискретные значения, вместо этого необходимо обратиться к модели, где признак развивается как некий непрерывный процесс. Вывод предковых состояний с помощью максимального правдоподобия (или байесовских методов) будет происходить так же, как и выше, но с вероятностями переходов в состоянии между соседними узлами, заданными некоторым другим непрерывным распределением вероятностей.

- Броуновское движение : в этом случае, если узлы и являются смежными в филогении (например, является предком ) и разделены ветвью длиной , вероятность перехода из состояния в состояние задается гауссовой плотностью со средним значением и дисперсией В этом случае имеется только один параметр ( ), и модель предполагает, что признак развивается свободно, без смещения в сторону увеличения или уменьшения, и что скорость изменения постоянна на всех ветвях филогенетического дерева. [50]
- Процесс Орнштейна-Уленбека : вкратце, процесс Орнштейна-Уленбека — это непрерывный стохастический процесс, который ведет себя как броуновское движение, но притягивается к некоторому центральному значению, где сила притяжения увеличивается с расстоянием от этого значения. [51] [52] [53] Это полезно для моделирования сценариев, в которых признак подвергается стабилизирующему отбору вокруг определенного значения (например, ). В рамках этой модели описанный выше переход из состояния в состояние будет иметь вероятность, определяемую плотностью перехода процесса Орнштейна-Уленбека с двумя параметрами: , который описывает дисперсию движущего броуновского движения, и , который описывает силу его притяжения к . По мере того как стремится к , процесс все меньше и меньше ограничивается своим притяжением к , и процесс становится броуновским движением. Из-за этого модели могут быть вложенными, и могут быть выполнены тесты отношения логарифмического правдоподобия, определяющие, какая из двух моделей является подходящей. [50]
- Стабильные модели непрерывной эволюции признаков: [54] хотя броуновское движение привлекательно и поддается обработке как модель непрерывной эволюции, оно не допускает ненейтральности в своей базовой форме и не предусматривает никаких изменений в скорости эволюции с течением времени. Вместо этого можно использовать стабильный процесс , значения которого в фиксированные моменты времени распределены как стабильные распределения , для моделирования эволюции признаков. Стабильные процессы, грубо говоря, ведут себя как броуновские движения, которые также включают прерывистые скачки. Это позволяет соответствующим образом моделировать сценарии, в которых ожидаются короткие всплески быстрой эволюции признаков. В этой обстановке методы максимального правдоподобия плохо подходят из-за неровной поверхности правдоподобия и потому, что вероятность может быть сделана произвольно большой, поэтому байесовские методы более уместны. [54]
Приложения
Эволюция характера
Реконструкция предков широко используется для выведения экологических, фенотипических или биогеографических признаков, связанных с предковыми узлами в филогенетическом дереве. Все методы реконструкции предковых признаков имеют подводные камни, поскольку они используют математические модели для прогнозирования того, как признаки изменились при большом количестве отсутствующих данных. Эти отсутствующие данные включают состояния вымерших видов, относительные скорости эволюционных изменений, знание начальных состояний признаков и точность филогенетических деревьев. Во всех случаях, когда используется реконструкция предковых признаков, результаты должны быть обоснованы с помощью изучения биологических данных, которые поддерживают выводы, основанные на модели. Гриффит О.В. и др. [55]
Реконструкция предков позволяет изучать эволюционные пути, адаптивный отбор , экспрессию генов развития, [56] [57] и функциональную дивергенцию эволюционного прошлого. Для обзора биологических и вычислительных методов реконструкции предков см. Chang et al. . [58] Для критики методов вычисления реконструкции предков см. Williams PD et al. . [13]
Эволюция поведения и жизненного цикла
У рогатых ящериц (род Phrynosoma ) живорождение развивалось многократно, основываясь на методах реконструкции предков. [59]
Реконструкция рациона питания галапагосских вьюрков
Для радиации вьюрков, населяющих Галапагосские острова , доступны как филогенетические, так и характерные данные . Эти данные позволяют проверять гипотезы относительно сроков и порядка изменений состояния признаков с течением времени посредством реконструкции предкового состояния. В сухой сезон рацион 13 видов галапагосских вьюрков можно разделить на три широкие категории рационов: во-первых, те, которые потребляют зерноподобную пищу, считаются « зерноядными », те, которые поедают членистоногих, называются « насекомоядными », а те, которые потребляют растительность, классифицируются как « листоядные ». [23] Реконструкция диетического предкового состояния с использованием максимальной бережливости восстанавливает 2 основных перехода от насекомоядного состояния: один к зерноядности и один к листоядности. Реконструкция предкового состояния с максимальным правдоподобием восстанавливает в целом схожие результаты, с одним существенным отличием: общий предок кладов древесного вьюрка ( Camarhynchus ) и земляного вьюрка ( Geospiza ) скорее всего зерноядный, а не насекомоядный (судя по бережливости). В этом случае эта разница между предковыми состояниями, возвращаемыми с помощью максимальной бережливости и максимального правдоподобия, вероятно, возникает в результате того факта, что оценки ML учитывают длины ветвей филогенетического дерева. [23]
Эволюция морфологических и физиологических признаков
Ящерицы -фриносоматиды демонстрируют замечательное морфологическое разнообразие, в том числе в относительном составе типов мышечных волокон в мышцах задних конечностей . Реконструкция предка, основанная на экономии квадратичных изменений (эквивалентной максимальному правдоподобию при эволюции характера броуновского движения [60] ), указывает на то, что рогатые ящерицы , один из трех основных субкладов этой линии, претерпели значительное эволюционное увеличение доли быстроокислительных гликолитических волокон в своих подвздошно-малоберцовых мышцах. [61]
Масса тела млекопитающих
В анализе массы тела 1679 видов плацентарных млекопитающих , сравнивающих стабильные модели непрерывной эволюции признаков с моделями броуновского движения , Эллиот и Мурс [54] показали, что эволюционный процесс, описывающий эволюцию массы тела млекопитающих, лучше всего характеризуется стабильной моделью непрерывной эволюции признаков, которая учитывает редкие изменения большой величины. В стабильной модели предковые млекопитающие сохраняли низкую массу тела в ходе ранней диверсификации, при этом большой прирост массы тела совпадал с происхождением нескольких отрядов видов с большой массой тела (например, копытных). Напротив, моделирование в рамках модели броуновского движения восстановило менее реалистичную, на порядок большую массу тела среди предковых млекопитающих, что потребовало значительного уменьшения размера тела до эволюции отрядов, демонстрирующих малый размер тела (например, грызунов ). Таким образом, стабильные модели восстанавливают более реалистичную картину эволюции массы тела млекопитающих, позволяя большим преобразованиям происходить на небольшом подмножестве ветвей. [54]
Соответствующая эволюция характера
Филогенетические сравнительные методы (выводы, сделанные путем сравнения родственных таксонов) часто используются для идентификации биологических характеристик, которые не развиваются независимо, что может выявить лежащую в основе зависимость. Например, эволюция формы клюва вьюрка может быть связана с его поведением при поиске пищи. Однако не рекомендуется искать эти ассоциации путем прямого сравнения измерений или генетических последовательностей, поскольку эти наблюдения не являются независимыми из-за их происхождения от общих предков. Для дискретных признаков эта проблема была впервые рассмотрена в рамках максимальной экономии путем оценки того, имеют ли два признака тенденцию претерпевать изменения на одних и тех же ветвях дерева. [62] [63] Фельзенштейн определил эту проблему для непрерывной эволюции признаков и предложил решение, похожее на предковую реконструкцию, в котором филогенетическая структура данных была размещена статистически путем направления анализа посредством вычисления «независимых контрастов» между узлами дерева, связанными неперекрывающимися ветвями. [28]
Молекулярная эволюция
На молекулярном уровне аминокислотные остатки в разных местах белка могут эволюционировать не независимо, поскольку они имеют прямое физико-химическое взаимодействие, или косвенно через их взаимодействия с общим субстратом или через дальнодействующие взаимодействия в структуре белка. И наоборот, складчатая структура белка потенциально может быть выведена из распределения взаимодействий остатков. [64] Одно из самых ранних применений предковой реконструкции, для предсказания трехмерной структуры белка через контакты остатков, было опубликовано Шиндяловым и коллегами. [65] Филогении, связывающие 67 различных семейств белков, были получены с помощью метода кластеризации на основе расстояния ( метод невзвешенной парной группы со средним арифметическим , UPGMA), а предковые последовательности были реконструированы с помощью экономии. Авторы сообщили о слабой, но значимой тенденции к тому, что совместно эволюционирующие пары остатков будут совместно расположены в известной трехмерной структуре белков.
Реконструкция древних белков и последовательностей ДНК только недавно стала значительным научным начинанием. Развитие обширных баз данных геномных последовательностей в сочетании с достижениями в области биотехнологии и методов филогенетического вывода сделало реконструкцию предков дешевой, быстрой и научно практичной. Эта концепция была применена для идентификации коэволюционирующих остатков в последовательностях белков с использованием более продвинутых методов реконструкции филогений и последовательностей предков. Например, реконструкция предков использовалась для идентификации коэволюционирующих остатков в белках, кодируемых геномами РНК-вирусов, в частности, ВИЧ. [66] [67] [68]
Реконструкция предкового белка и ДНК позволяет воссоздать эволюцию белка и ДНК в лабораторных условиях, чтобы ее можно было изучать напрямую. [58] Что касается белков, это позволяет исследовать эволюцию современной молекулярной структуры и функции. Кроме того, реконструкция предкового белка может привести к открытию новых биохимических функций, которые были утрачены в современных белках. [69] [70] Она также позволяет получить представление о биологии и экологии вымерших организмов. [71] Хотя большинство реконструкций предков касалось белков, она также использовалась для проверки эволюционных механизмов на уровне бактериальных геномов [72] и последовательностей генов приматов. [73]
Разработка вакцины
РНК-вирусы, такие как вирус иммунодефицита человека (ВИЧ), развиваются чрезвычайно быстро, на порядки быстрее, чем млекопитающие или птицы. Для этих организмов предковая реконструкция может применяться в гораздо более коротких временных масштабах; например, для того, чтобы реконструировать глобального или регионального предшественника эпидемии, которая охватывала десятилетия, а не миллионы лет. Группа под руководством Брайана Гашена предложила [74] , чтобы такие реконструированные штаммы использовались в качестве целей для разработки вакцин , а не последовательностей, выделенных у пациентов в настоящее время. Поскольку ВИЧ чрезвычайно разнообразен, вакцина, разработанная для работы с вирусной популяцией одного пациента, может не сработать для другого пациента, поскольку эволюционное расстояние между этими двумя вирусами может быть большим. Однако их последний общий предок ближе к каждому из двух вирусов, чем они друг к другу. Таким образом, вакцина, разработанная для общего предка, может иметь больше шансов быть эффективной для большей доли циркулирующих штаммов. Другая группа ученых развила эту идею дальше, разработав метод реконструкции центра дерева для получения последовательности, общее эволюционное расстояние которой до современных штаммов было бы как можно меньше. [75] Строго говоря, этот метод не был реконструкцией предков , поскольку последовательность центра дерева (COT) не обязательно представляет собой последовательность, которая когда-либо существовала в эволюционной истории вируса. Однако Ролланд и его коллеги обнаружили, что в случае ВИЧ вирус COT был функциональным при синтезе. Аналогичные эксперименты с синтетическими последовательностями предков, полученными путем реконструкции максимального правдоподобия, также показали, что эти предки являются как функциональными, так и иммуногенными, [76] [77] что придает этим методам некоторую достоверность. Кроме того, реконструкция предков может быть потенциально использована для выведения генетической последовательности переданных вариантов ВИЧ, которые пошли на установление следующей инфекции, с целью выявления отличительных характеристик этих вариантов (как неслучайного выбора переданной популяции вирусов), которые могут быть направлены на разработку вакцины. [78]
Перестройки генома
Вместо того, чтобы выводить последовательность ДНК предка, можно заинтересоваться более масштабной молекулярной структурой и содержанием генома предка. Эта проблема часто решается в комбинаторной структуре, путем моделирования геномов как перестановок генов или гомологичных областей. Различные операции разрешены для этих перестановок, такие как инверсия (сегмент перестановки переворачивается на месте), делеция (сегмент удаляется), транспозиция (сегмент удаляется из одной части перестановки и вставляется в другое место) или получение генетического содержания посредством рекомбинации , дупликации или горизонтального переноса генов . «Проблема перестройки генома», впервые поставленная Уоттерсоном и коллегами [17] , спрашивает: учитывая два генома (перестановки) и набор допустимых операций, какова кратчайшая последовательность операций, которая преобразует один геном в другой? Обобщением этой проблемы, применимым к реконструкции предков, является «задача множественной перестройки генома»: [79] учитывая набор геномов и набор допустимых операций, найти (i) бинарное дерево с заданными геномами в качестве его листьев, и (ii) назначение геномов внутренним узлам дерева, таким образом, чтобы общее число операций по всему дереву было минимальным. Этот подход похож на экономичность, за исключением того, что дерево выводится вместе с последовательностями предков. К сожалению, даже задача перестройки одного генома является NP-трудной , [80] хотя ей уделялось много внимания в математике и информатике (для обзора см. Fertin и коллеги [81] ).
Реконструкция геномов предков также называется реконструкцией кариотипа . В настоящее время основным экспериментальным методом является окраска хромосом. [82] [83] Недавно исследователи разработали вычислительные методы для реконструкции кариотипа предков, используя преимущества сравнительной геномики . [84] [85] Кроме того, сравнительная геномика и реконструкция генома предков применялись для идентификации древних событий горизонтального переноса генов у последнего общего предка линии (например, Candidatus Accumulibacter phosphatis [86] ) для определения эволюционной основы приобретения признаков.
Пространственные приложения
Миграция
Реконструкция предков не ограничивается биологическими признаками. Пространственное расположение также является признаком, и методы реконструкции предков могут вывести местоположение предков рассматриваемых особей. Такие методы были использованы Леми и коллегами [16] для географического отслеживания предков 192 штаммов птичьего гриппа A-H5N1, отобранных из двадцати мест в Европе и Азии, и для 101 последовательности вируса бешенства , отобранных из двенадцати африканских стран.
Рассмотрение местоположений как дискретных состояний (страны, города и т. д.) позволяет применять модели дискретных состояний, описанные выше. Однако, в отличие от модели, где пространство состояний для признака невелико, может быть много местоположений, и переходы между определенными парами состояний могут происходить редко или никогда не происходить; например, миграция между отдаленными местами может никогда не происходить напрямую, если между двумя местами не существует воздушного сообщения, поэтому такие миграции должны сначала проходить через промежуточные места. Это означает, что в модели может быть много параметров, которые равны нулю или близки к нулю. С этой целью Лемей и коллеги использовали байесовскую процедуру не только для оценки параметров и предковых состояний, но и для выбора параметров миграции, не равных нулю; их работа предполагает, что эта процедура приводит к более эффективному использованию данных. Они также изучают использование априорных распределений, которые включают географическую структуру или гипотезы о динамике миграции, обнаружив, что те, которые они рассматривали, не оказали большого влияния на результаты.
Используя этот анализ, команда вокруг Лемея обнаружила, что наиболее вероятным центром распространения A-H5N1 является Гуандун , а Гонконг также получает последующую поддержку. Кроме того, их результаты подтверждают гипотезу о давнем присутствии африканского бешенства в Западной Африке .
Ареалы видов
Выведение исторических биогеографических моделей часто требует реконструкции ареалов предков видов на филогенетических деревьях. [87] Например, хорошо решенная филогения видов растений в роде Cyrtandra [87] использовалась вместе с информацией об их географических ареалах для сравнения четырех методов реконструкции ареалов предков. Команда сравнила парсимонию Фитча, [20] (FP; парсимония) стохастическое картирование [88] (SM; максимальное правдоподобие), анализ дисперсии-викариантности [89] (DIVA; парсимония) и дисперсия-вымирание-кладогенез [15] [90] (DEC; максимальное правдоподобие). Результаты показали, что оба метода парсимонии работали плохо, что, вероятно, было связано с тем, что методы парсимонии не учитывают длины ветвей. Оба метода максимального правдоподобия работали лучше; однако анализы DEC, которые дополнительно позволяют включать геологические априорные данные, дали более реалистичные выводы об эволюции ареала в Cyrtandra по сравнению с другими методами. [87]
Другой метод максимального правдоподобия восстанавливает филогеографическую историю гена [91] путем реконструкции предковых местоположений выбранных таксонов. Этот метод предполагает пространственно явную модель случайного блуждания миграции для реконструкции предковых местоположений с учетом географических координат особей, представленных вершинами филогенетического дерева. При применении к филогенетическому дереву хоровых лягушек Pseudacris feriarum этот метод восстановил недавнюю экспансию на север, более высокое расстояние рассеивания на поколение в недавно колонизированном регионе, нецентральное предковое местоположение и направленную миграцию. [91]

Первое рассмотрение проблемы множественной перестройки генома, задолго до ее формализации в терминах перестановок, было представлено Стертевантом и Добжанским в 1936 году. [92] Они исследовали геномы нескольких штаммов плодовой мушки из разных географических мест и заметили, что одна конфигурация, которую они назвали «стандартной», была наиболее распространенной во всех изученных областях. Примечательно, что они также заметили, что четыре различных штамма можно получить из стандартной последовательности с помощью одной инверсии, а два других можно было связать с помощью второй инверсии. Это позволило им выдвинуть гипотезу о филогении последовательностей и сделать вывод, что стандартная последовательность, вероятно, также была предковой.
Лингвистическая эволюция
Реконструкции слов и феноменов древних протоязыков, таких как протоиндоевропейский, были выполнены на основе наблюдаемых аналогов в современных языках. Обычно эти анализы проводятся вручную с использованием «сравнительного метода». [93] Во-первых, слова из разных языков с общей этимологией ( когнаты ) идентифицируются в современных изучаемых языках, аналогично идентификации ортологичных биологических последовательностей. Во-вторых, идентифицируются соответствия между отдельными звуками в когнатах, шаг, аналогичный выравниванию биологических последовательностей , хотя и выполняется вручную. Наконец, вероятные предковые звуки предполагаются путем ручного осмотра и различных эвристик (например, тот факт, что большинство языков имеют как носовые, так и неносовые гласные ). [93]
Программное обеспечение
Существует множество программных пакетов, которые могут выполнять реконструкцию предкового состояния. Как правило, эти программные пакеты разрабатываются и поддерживаются усилиями ученых в смежных областях и выпускаются по лицензиям свободного программного обеспечения . Следующая таблица не претендует на исчерпывающую детализацию всех доступных пакетов, но представляет собой репрезентативный пример обширного разнообразия пакетов, реализующих методы реконструкции предков с различными сильными сторонами и функциями.
| Имя | Методы | Платформа | Входы | ! Типы персонажей | Непрерывные (C) или дискретные символы (D) | Лицензия на программное обеспечение |
|---|---|---|---|---|---|---|
| ПАМЛ | Максимальное Правдоподобие | Unix, Mac, Винда | ФИЛИПП, НЕКСУС, ФАСТ | Нуклеотид, Белок | Д | Стандартная общественная лицензия GNU , версия 3 |
| ЗВЕРЬ | байесовский | Unix, Mac, Винда | NEXUS, ЗВЕРЬ XML | Нуклеотид, Белок, Географический | С, Д | Стандартная общественная лицензия ограниченного применения GNU |
| фитоинструменты | Максимальное Правдоподобие | Unix, Mac, Винда | newick, нексус | Качественные и количественные признаки | С, Д | Стандартная общественная лицензия GNU |
| Обезьяна | Максимальное Правдоподобие | Unix, Mac, Винда | НЕКСУС, ФАСТ, КЛУСТАЛ | Нуклеотид, Белок | С, Д | Стандартная общественная лицензия GNU |
| Diversitree | Максимальное Правдоподобие | Unix, Mac, Винда | НЕКСУС | Качественные и количественные признаки, Географические | С, Д | Стандартная общественная лицензия GNU, версия 2 |
| ХайФи | Максимальное Правдоподобие | Unix, Mac, Винда | МЕГА, НЕКСУС, ФАСТА, ФИЛИПП | Нуклеотид, Белок (настраиваемый) | Д | Лицензия свободной документации GNU 1.3 |
| БайесХарактеристики | байесовский | Unix, Mac, Винда | TSV или таблица с разделителями-пробелами. Строки — виды, столбцы — признаки. | Качественные и количественные признаки | С, Д | Лицензия Creative Commons Attribution |
| Лагранж | Максимальное Правдоподобие | Linux, Mac, Винда | TSV/CSV видов регионов. Строки — виды, столбцы — географические регионы. | Географический | - | Стандартная общественная лицензия GNU, версия 2 |
| Мескит | Экономия, максимальное правдоподобие | Unix, Mac, Винда | Фаста, НБРФ, Генбанк, PHYLIP, CLUSTAL, ТСВ | Нуклеотид, Белок, Географический | С, Д | Лицензия Creative Commons Attribution 3.0 |
| Филомаппер | Максимальное правдоподобие, байесовский (начиная с версии 2) | Unix, Mac, Винда | НЕКСУС | Географическая, Экологическая ниша | С, Д | - |
| Предки | Максимальное Правдоподобие | Веб | Фаста | Нуклеотид (инделы) | Д | - |
| Фирекс | Максимальная бережливость | линукс | Фаста | Экспрессия генов | С, Д | Запатентованный |
| SIMMAP | Стохастическое картирование | Мак | Формат, подобный XML | Нуклеотид, качественные признаки | Д | Запатентованный |
| MrBayes | байесовский | Unix, Mac, Винда | НЕКСУС | Нуклеотид, Белок | Д | Стандартная общественная лицензия GNU |
| ПАРАНА | Максимальная бережливость | Unix, Mac, Винда | Ньюик | Биологические сети | Д | Лицензия Apache |
| ФАСТ (ПРИКВЕЛ) | Максимальное Правдоподобие | Unix, Mac, Винда | Множественное выравнивание | Нуклеотид | Д | Лицензия BSD |
| РАСП | Максимальное правдоподобие, байесовский | Unix, Mac, Винда | Ньюик | Географический | Д | - |
| ВИП | Максимальная бережливость | Linux, Вин | Ньюик | Географический | D (сетка) | GPL Творческие общие права |
| FastML | Максимальное Правдоподобие | Веб, Unix | Фаста | Нуклеотид, Белок | Д | Авторские права |
| МЛГО | Максимальная вероятность | Веб | Обычай | Перестановка порядка генов | Д | ГНУ |
| БАРСУК | байесовский | Unix, Mac, Винда | Обычай | Перестановка порядка генов | Д | GNU GPL версия 2 |
| СЧИТАТЬ | Максимальная экономия, максимальное правдоподобие | Unix, Mac, Винда | Текстовый файл с разделителями-табуляциями, содержащий строки для таксонов и данные по количеству в столбцах. | Подсчет (численные) данные (например, размер семейства гомологов) | Д | БСД |
| МЕГА | Максимальная экономия, максимальная правдоподобность. | Мак, Вин | МЕГА | Нуклеотид, Белок | Д | Запатентованный |
| АНЖЕС | Местная бережливость | Unix | Обычай | Карты генома | Д | Стандартная общественная лицензия GNU, версия 3 |
| РАСШИФРОВАТЬ | Максимальное Правдоподобие | Unix, Mac, Винда | FASTA, ГенБанк | Нуклеотид | Д | Стандартная общественная лицензия GNU, версия 3 |
| ЕРЭМ | Максимальная вероятность. | Win, Unix, модуль Matlab | Пользовательский текстовый формат для параметров модели, дерева, наблюдаемых значений символов. | Двоичный | Д | Не указано, хотя на сайте указано, что программное обеспечение доступно бесплатно. |
Описания пакетов
Молекулярная эволюция
Большинство этих программных пакетов предназначены для анализа данных генетических последовательностей. Например, PAML [94] представляет собой набор программ для филогенетического анализа выравниваний последовательностей ДНК и белков по максимальному правдоподобию. Реконструкция предков может быть выполнена с помощью программы codeml . Кроме того, LAZARUS представляет собой набор скриптов Python , которые оборачивают функции реконструкции предков PAML для пакетной обработки и большей простоты использования. [95] Такие программные пакеты, как MEGA , HyPhy и Mesquite, также выполняют филогенетический анализ данных последовательностей, но разработаны так, чтобы быть более модульными и настраиваемыми. HyPhy [96] реализует совместный метод максимального правдоподобия реконструкции предковой последовательности [7], который можно легко адаптировать для реконструкции более обобщенного диапазона дискретных состояний предковых признаков, таких как географические местоположения, путем указания настраиваемой модели в его пакетном языке. Mesquite [97] предоставляет методы реконструкции состояния предков как для дискретных, так и для непрерывных признаков, используя как методы максимальной экономии, так и методы максимального правдоподобия. Он также предоставляет несколько инструментов визуализации для интерпретации результатов реконструкции предков. MEGA [98] также является модульной системой, но делает больший упор на простоту использования, чем на настройку анализов. Начиная с версии 5, MEGA позволяет пользователю реконструировать состояния предков, используя методы максимальной экономии, максимального правдоподобия и эмпирические методы Байеса. [98]
Байесовский анализ генетических последовательностей может придать большую надежность неверной спецификации модели. MrBayes [99] позволяет делать выводы о предковых состояниях в предковых узлах, используя полный иерархический байесовский подход. Программа PREQUEL, распространяемая в пакете PHAST [100], выполняет сравнительную эволюционную геномику, используя реконструкцию предковой последовательности. SIMMAP [101] стохастически отображает мутации в филогениях. BayesTraits [31] анализирует дискретные или непрерывные признаки в байесовской структуре для оценки моделей эволюции, реконструкции предковых состояний и обнаружения коррелированной эволюции между парами признаков.
Другие типы персонажей
Другие программные пакеты больше ориентированы на анализ качественных и количественных признаков ( фенотипов ). Например, пакет ape [102] в статистической вычислительной среде R также предоставляет методы реконструкции предкового состояния как для дискретных, так и для непрерывных признаков через функцию ' ace ', включая максимальное правдоподобие. Phyrex реализует алгоритм на основе максимальной экономии для реконструкции профилей экспрессии предковых генов, в дополнение к методу максимального правдоподобия для реконструкции предковых генетических последовательностей (путем обертывания вокруг функции baseml в PAML). [103]
Несколько программных пакетов также реконструируют филогеографию . BEAST (байесовский эволюционный анализ с помощью деревьев выборки) [104] и BEAST 2 предоставляют инструменты для реконструкции предковых географических местоположений из наблюдаемых последовательностей, аннотированных данными о местоположении, с использованием байесовских методов выборки MCMC . Diversitree [105] — это пакет R, предоставляющий методы для реконструкции предкового состояния в соответствии с моделями Mk2 ( непрерывная марковская модель эволюции бинарных признаков) [106] и BiSSE (бинарное состояние видообразования и вымирания). Lagrange выполняет анализы по реконструкции эволюции географического ареала на филогенетических деревьях. [15] Phylomapper [91] — это статистическая структура для оценки исторических закономерностей потока генов и предковых географических местоположений. RASP [107] выводит предковые состояния с помощью статистического анализа дисперсии-викариантности, методов Лагранжа, Байеса-Лагранжа, BayArea и BBM. VIP [108] выводит историческую биогеографию, исследуя разрозненные географические распределения.
Перестройки генома предоставляют ценную информацию в сравнительной геномике между видами. ANGES [109] сравнивает существующие родственные геномы посредством реконструкции предков генетических маркеров. BADGER [110] использует байесовский подход к изучению истории перестройки генов. Count [111] реконструирует эволюцию размера семейств генов. EREM [112] анализирует приобретение и потерю генетических признаков, кодируемых бинарными символами. PARANA [113] выполняет вывод на основе экономии предковых биологических сетей, которые представляют потерю и дупликацию генов.
Веб-приложения
Наконец, существует несколько приложений на основе веб-сервера, которые позволяют исследователям использовать методы максимального правдоподобия для реконструкции предков различных типов признаков без необходимости установки какого-либо программного обеспечения. Например, Ancestors [114] — это веб-сервер для реконструкции генома предков путем идентификации и расположения синтенных регионов. FastML [115] — это веб-сервер для вероятностной реконструкции последовательностей предков методом максимального правдоподобия, который использует модель пробельных признаков для реконструкции вариации инделей . MLGO [116] — это веб-сервер для анализа порядка генов с максимальным правдоподобием.
Будущие направления
Разработка и применение вычислительных алгоритмов для реконструкции предков продолжает оставаться активной областью исследований в различных дисциплинах. Например, реконструкция вставок и делеций последовательностей (инделей) отстает от более простого применения моделей замещения. Бушар-Коте и Джордан недавно описали новую модель (процесс Пуассона-инделей) [117] , которая представляет собой важный шаг вперед по сравнению с архетипической моделью эволюции инделей Торна-Кишино-Фельзенштейна. [118] Кроме того, эта область продвигается вперед благодаря быстрому прогрессу в области технологии секвенирования следующего поколения , где последовательности генерируются из миллионов шаблонов нуклеиновых кислот путем обширного распараллеливания реакций секвенирования в специальном аппарате. Эти достижения позволили создать «глубокий» снимок генетического состава быстро эволюционирующей популяции, такой как РНК-вирусы [119] или опухолевые клетки [120] за относительно короткий промежуток времени. В то же время огромный объем данных и специфичные для платформы профили ошибок секвенирования создали новые биоинформационные проблемы при обработке этих данных для реконструкции предковых последовательностей.
Смотрите также
- Эволюционная биология
- Происхождение жизни
- Распущенность ферментов
- Реконструкция последовательности предков
Ссылки
 Эта статья была адаптирована из следующего источника по лицензии CC BY 4.0 (2015) (отчеты рецензента): Jeffrey B Joy; Richard H Liang; Rosemary M McCloskey; T Nguyen; Art Poon (12 июля 2016 г.). "Ancestral Reconstruction". PLOS Computational Biology . 12 (7): e1004763. doi : 10.1371/JOURNAL.PCBI.1004763 . ISSN 1553-734X. PMC 4942178. PMID 27404731. Wikidata Q28596371 .
Эта статья была адаптирована из следующего источника по лицензии CC BY 4.0 (2015) (отчеты рецензента): Jeffrey B Joy; Richard H Liang; Rosemary M McCloskey; T Nguyen; Art Poon (12 июля 2016 г.). "Ancestral Reconstruction". PLOS Computational Biology . 12 (7): e1004763. doi : 10.1371/JOURNAL.PCBI.1004763 . ISSN 1553-734X. PMC 4942178. PMID 27404731. Wikidata Q28596371 .
- ^ ab Omland KE (1999). «Предположения и проблемы реконструкций предкового состояния». Systematic Biology . 48 (3): 604–611. doi : 10.1080/106351599260175 . ISSN 1063-5157.
- ^ Cai W, Pei J, Grishin NV (сентябрь 2004 г.). «Реконструкция последовательностей предковых белков и ее применение». BMC Evolutionary Biology . 4 (1): 33. doi : 10.1186/1471-2148-4-33 . PMC 522809. PMID 15377393 .
- ^ Platnick NI, Cameron HD (1977). «Кладистические методы в текстовом, лингвистическом и филогенетическом анализе». Systematic Zoology . 26 (4): 380–385. doi :10.2307/2412794. ISSN 0039-7989. JSTOR 2412794.
- ^ Tehrani JJ (2013). «Филогения Красной Шапочки». PLOS ONE . 8 (11): e78871. Bibcode : 2013PLoSO...878871T. doi : 10.1371 /journal.pone.0078871 . PMC 3827309. PMID 24236061.
- ^ Уокер RS, Хилл KR, Флинн MV, Эллсворт RM (апрель 2011 г.). «Эволюционная история брачных практик охотников-собирателей». PLOS ONE . 6 (4): e19066. Bibcode : 2011PLoSO...619066W. doi : 10.1371/journal.pone.0019066 . PMC 3083418. PMID 21556360 .
- ^ Брукс DR (1999). «Филогения и сравнительный метод в поведении животных», под редакцией Эмии П. Мартинс, Oxford University Press, 1996. X+415 стр. Поведенческие процессы . 47 (2): 135–136. doi :10.1016/S0376-6357(99)00038-8. ISSN 0376-6357. PMID 24896936. S2CID 9872907.
- ^ abc Pupko T, Pe'er I, Shamir R, Graur D (июнь 2000 г.). "Быстрый алгоритм для совместной реконструкции предковых аминокислотных последовательностей". Молекулярная биология и эволюция . 17 (6): 890–896. doi :10.1093/oxfordjournals.molbev.a026369. PMID 10833195.
- ^ abc Pagel M, Meade A, Barker D (октябрь 2004 г.). «Байесовская оценка состояний предковых признаков в филогениях». Systematic Biology . 53 (5): 673–684. CiteSeerX 10.1.1.483.4931 . doi : 10.1080/10635150490522232 . PMID 15545248.
- ^ Sanger F, Thompson EO, Kitai R (март 1955). «Амидные группы инсулина». The Biochemical Journal . 59 (3): 509–518. doi :10.1042/bj0590509. PMC 1216278. PMID 14363129 .
- ^ Полинг Л., Цукеркандл Э., Хенриксен Т., Лёвстад Р. (1963). «Химическая палеогенетика. Молекулярные «реставрационные исследования» вымерших форм жизни». Acta Chemica Scandinavica . 17 (приложение): 9–16. doi : 10.3891/acta.chem.scand.17s-0009 . ISSN 0904-213X.
- ^ ab Dobzhansky T, Sturtevant AH (январь 1938). «Инверсии в хромосомах Drosophila Pseudoobscura». Genetics . 23 (1): 28–64. doi :10.1093/genetics/23.1.28. PMC 1209001 . PMID 17246876.
- ^ Harms MJ, Thornton JW (июнь 2010 г.). «Анализ структуры и функции белка с использованием реконструкции предковых генов». Current Opinion in Structural Biology . 20 (3): 360–366. doi :10.1016/j.sbi.2010.03.005. PMC 2916957. PMID 20413295 .
- ^ abcd Williams PD, Pollock DD, Blackburne BP, Goldstein RA (июнь 2006 г.). «Оценка точности методов реконструкции предковых белков». PLOS Computational Biology . 2 (6): e69. Bibcode : 2006PLSCB ...2...69W. doi : 10.1371/journal.pcbi.0020069 . PMC 1480538. PMID 16789817.
- ^ Ронквист Ф. (сентябрь 2004 г.). «Байесовский вывод об эволюции признаков». Тенденции в экологии и эволюции . 19 (9): 475–481. doi :10.1016/j.tree.2004.07.002. PMID 16701310.
- ^ abc Ree RH, Smith SA (февраль 2008 г.). «Вывод максимального правдоподобия об эволюции географического ареала путем рассеивания, локального вымирания и кладогенеза». Systematic Biology . 57 (1): 4–14. CiteSeerX 10.1.1.457.2776 . doi : 10.1080/10635150701883881 . PMID 18253896.
- ^ ab Lemey P, Rambaut A, Drummond AJ, Suchard MA (сентябрь 2009 г.). «Байесовская филогеография находит свои корни». PLOS Computational Biology . 5 (9): e1000520. Bibcode : 2009PLSCB...5E0520L. doi : 10.1371/journal.pcbi.1000520 . PMC 2740835. PMID 19779555 .
- ^ ab Watterson GA, Ewens WJ, Hall TE, Morgan A (1982). «Проблема инверсии хромосом». Журнал теоретической биологии . 99 (1): 1–7. Bibcode : 1982JThBi..99....1W. doi : 10.1016/0022-5193(82)90384-8. ISSN 0022-5193.
- ^ Tuffley C, Steel M (май 1997). «Связи между максимальным правдоподобием и максимальной экономией в рамках простой модели замещения сайтов». Bulletin of Mathematical Biology . 59 (3): 581–607. CiteSeerX 10.1.1.22.6143 . doi :10.1007/BF02459467. PMID 9172826. S2CID 189885872.
- ^ Своффорд DL, Мэддисон WP (1987). «Реконструкция предковых состояний характера в условиях бережливости Вагнера». Mathematical Biosciences . 87 (2): 199–229. doi :10.1016/0025-5564(87)90074-5. ISSN 0025-5564.
- ^ ab Fitch WM (1971). «К определению курса эволюции: минимальное изменение для определенной топологии дерева». Систематическая зоология . 20 (4): 406–416. doi :10.2307/2412116. ISSN 0039-7989. JSTOR 2412116.
- ^ Stamatakis A (ноябрь 2006 г.). «RAxML-VI-HPC: филогенетический анализ на основе максимального правдоподобия с тысячами таксонов и смешанными моделями» (PDF) . Биоинформатика . 22 (21): 2688–2690. doi : 10.1093/bioinformatics/btl446 . PMID 16928733.
- ^ Sankoff D (1975). «Минимальные мутационные деревья последовательностей». Журнал SIAM по прикладной математике . 28 (1): 35–42. CiteSeerX 10.1.1.665.9596 . doi :10.1137/0128004. ISSN 0036-1399.
- ^ abcde Schluter D, Price T, Mooers AØ, Ludwig D (декабрь 1997 г.). «Вероятность состояний предков при адаптивной радиации». Эволюция; Международный журнал органической эволюции . 51 (6): 1699–1711. doi :10.2307/2410994. JSTOR 2410994. PMID 28565128.
- ^ Фельзенштейн Дж (1973). «Методы максимального правдоподобия и минимальных шагов для оценки эволюционных деревьев по данным о дискретных признаках». Систематическая зоология . 22 (3): 240–249. doi :10.2307/2412304. ISSN 0039-7989. JSTOR 2412304.
- ^ abc Cunningham CW, Omland KE, Oakley TH (сентябрь 1998 г.). «Реконструкция предковых состояний характера: критическая переоценка». Trends in Ecology & Evolution . 13 (9): 361–366. Bibcode :1998TEcoE..13..361C. doi :10.1016/S0169-5347(98)01382-2. PMID 21238344. S2CID 6779286.
- ^ Mooers AØ, Schluter D (1999). «Реконструкция состояний предков с максимальным правдоподобием: поддержка моделей с одной и двумя скоростями». Systematic Biology . 48 (3): 623–633. CiteSeerX 10.1.1.594.175 . doi :10.1080/106351599260193. ISSN 1063-5157.
- ^ Li G, Steel M, Zhang L (август 2008 г.). «Больше таксонов не обязательно лучше для реконструкции предковых состояний признаков». Systematic Biology . 57 (4): 647–653. arXiv : 0803.0195 . doi :10.1080/10635150802203898. PMID 18709600. S2CID 1373201.
- ^ ab Felsenstein J (1985). «Филогении и сравнительный метод». The American Naturalist . 125 (1): 1–15. doi :10.1086/284325. ISSN 0003-0147. S2CID 9731499.
- ^ abcd Yang Z, Kumar S, Nei M (декабрь 1995 г.). «Новый метод вывода предковых нуклеотидных и аминокислотных последовательностей». Genetics . 141 (4): 1641–1650. doi :10.1093/genetics/141.4.1641. PMC 1206894 . PMID 8601501.
- ^ Koshi JM, Goldstein RA (февраль 1996). «Вероятностная реконструкция последовательностей предковых белков». Journal of Molecular Evolution . 42 (2): 313–320. Bibcode :1996JMolE..42..313K. CiteSeerX 10.1.1.1031.2646 . doi :10.1007/BF02198858. PMID 8919883. S2CID 15997589.
- ^ ab Pagel M (1999). «Подход максимального правдоподобия к реконструкции предковых состояний признаков дискретных признаков в филогениях». Systematic Biology . 48 (3): 612–622. doi : 10.1080/106351599260184 . ISSN 1063-5157.
- ^ Guindon S, Gascuel O (октябрь 2003 г.). «Простой, быстрый и точный алгоритм оценки больших филогений по максимальному правдоподобию». Systematic Biology . 52 (5): 696–704. CiteSeerX 10.1.1.110.5852 . doi : 10.1080/10635150390235520 . PMID 14530136.
- ^ Doornik JA, Ooms M (2003). «Вычислительные аспекты оценки максимального правдоподобия авторегрессионных дробно интегрированных моделей скользящего среднего». Computational Statistics & Data Analysis . 42 (3): 333–348. doi :10.1016/S0167-9473(02)00212-8. ISSN 0167-9473.
- ^ ab Felsenstein J (1981). «Эволюционные деревья из последовательностей ДНК: подход максимального правдоподобия». Журнал молекулярной эволюции . 17 (6): 368–376. Bibcode :1981JMolE..17..368F. doi :10.1007/BF01734359. PMID 7288891. S2CID 8024924.
- ^ Eyre-Walker A (декабрь 1998 г.). «Проблемы с экономией в последовательностях смещенного состава оснований». Журнал молекулярной эволюции . 47 (6): 686–690. Bibcode : 1998JMolE..47..686E. doi : 10.1007/PL00006427. PMID 9847410. S2CID 26128712.
- ^ Пупко Т., Пеер И., Хасегава М., Граур Д., Фридман Н. (август 2002 г.). «Алгоритм ветвей и границ для вывода предковых аминокислотных последовательностей, когда скорость замены варьируется между сайтами: применение к эволюции пяти семейств генов». Биоинформатика . 18 (8): 1116–1123. doi :10.1093/bioinformatics/18.8.1116. PMID 12176835.
- ^ Грюнхайт Н., Локхарт П.Дж., Стил М., Мартин В. (июль 2008 г.). «Трудности в тестировании коварионоподобных свойств последовательностей под влиянием изменяющихся пропорций вариабельных участков». Молекулярная биология и эволюция . 25 (7): 1512–1520. doi : 10.1093/molbev/msn098 . hdl : 10092/2637 . PMID 18424773.
- ^ Huelsenbeck JP, Ronquist F (август 2001 г.). «MRBAYES: байесовский вывод филогенетических деревьев». Биоинформатика . 17 (8): 754–755. doi : 10.1093/bioinformatics/17.8.754 . PMID 11524383.
- ^ Yang Z (октябрь 1997 г.). «PAML: программный пакет для филогенетического анализа по максимальному правдоподобию». Computer Applications in the Biosciences . 13 (5): 555–556. doi : 10.1093/bioinformatics/13.5.555 . PMID 9367129.
- ^ ab Huelsenbeck JP, Bollback JP (июнь 2001 г.). «Эмпирическая и иерархическая байесовская оценка предковых состояний». Systematic Biology . 50 (3): 351–366. CiteSeerX 10.1.1.319.4271 . doi :10.1080/106351501300317978. PMID 12116580.
- ^ Lutzoni F, Pagel M, Reeb V (июнь 2001 г.). «Основные грибковые линии происходят от симбиотических предков лишайников». Nature . 411 (6840): 937–940. Bibcode :2001Natur.411..937L. doi :10.1038/35082053. PMID 11418855. S2CID 4414913.
- ^ Hanson-Smith V, Kolaczkowski B, Thornton JW (сентябрь 2010 г.). «Надежность реконструкции предковой последовательности в условиях филогенетической неопределенности». Молекулярная биология и эволюция . 27 (9): 1988–1999. doi :10.1093/molbev/msq081. PMC 2922618. PMID 20368266 .
- ^ Hillis DM, Bull JJ, White ME, Badgett MR, Molineux IJ (январь 1992). «Экспериментальная филогенетика: генерация известной филогении». Science . 255 (5044): 589–592. Bibcode :1992Sci...255..589H. doi :10.1126/science.1736360. PMID 1736360.
- ^ Oakley TH, Cunningham CW (апрель 2000 г.). «Независимые контрасты достигают успеха там, где реконструкция предка терпит неудачу в известной филогении бактериофагов». Эволюция; Международный журнал органической эволюции . 54 (2): 397–405. doi :10.1554/0014-3820(2000)054[0397:ICSWAR]2.0.CO;2. PMID 10937216. S2CID 198153271.
- ^ Финарелли JA, Флинн JJ (апрель 2006 г.). «Реконструкция предкового состояния размера тела у Caniformia (Carnivora, Mammalia): эффекты включения данных из ископаемых летописей». Systematic Biology . 55 (2): 301–313. doi :10.1080/10635150500541698. PMID 16611601.
- ^ Albert JS, Johnson DM, Knouft JH (2009). «Ископаемые дают лучшие оценки размера тела предков, чем современные таксоны рыб». Acta Zoologica . 90 : 357–384. doi :10.1111/j.1463-6395.2008.00364.x. ISSN 0001-7272.
- ^ Slater GJ, Harmon LJ, Alfaro ME (декабрь 2012 г.). «Интеграция ископаемых с молекулярными филогениями улучшает вывод об эволюции признаков». Эволюция; Международный журнал органической эволюции . 66 (12): 3931–3944. doi : 10.1111/j.1558-5646.2012.01723.x . PMID 23206147. S2CID 24390146.
- ^ Webster AJ, Purvis A (январь 2002 г.). «Проверка точности методов реконструкции предковых состояний непрерывных признаков». Труды. Биологические науки . 269 (1487): 143–149. doi :10.1098/rspb.2001.1873. PMC 1690869. PMID 11798429 .
- ^ Maddison WP, Midford PE, Otto SP (октябрь 2007 г.). «Оценка влияния бинарного признака на видообразование и вымирание». Systematic Biology . 56 (5): 701–710. CiteSeerX 10.1.1.150.2224 . doi : 10.1080/10635150701607033 . PMID 17849325.
- ^ ab Martins EP (1994).«Оценка скорости фенотипической эволюции по сравнительным данным». American Naturalist . 144 (2): 193–209. doi :10.1086/285670. S2CID 85300707.
- ^ Фельзенштейн Дж. (1988). «Филогении и количественные признаки». Annual Review of Ecology and Systematics . 19 : 445–471. doi :10.1146/annurev.ecolsys.19.1.445.
- ^ Гарланд младший Т, Дикерман AW, Дженис CM, Джонс JA (1993). «Филогенетический анализ ковариации с помощью компьютерного моделирования». Систематическая биология . 42 (3): 265–292. doi :10.1093/sysbio/42.3.265.
- ^ Купер, Н., Г. Х. Томас, К. Вендитти, А. Мид и Р. П. Фреклтон. 2015. Предупреждение об использовании моделей Орнштейна-Уленбека в макроэволюционных исследованиях. Биологический журнал Линнеевского общества.
- ^ abcd Эллиот MG, Мурс AØ (ноябрь 2014 г.). «Вывод предковых состояний без предположения нейтральности или постепенности с использованием стабильной модели непрерывной эволюции признаков». BMC Evolutionary Biology . 14 (1): 226. arXiv : 1302.5104 . Bibcode :2014BMCEE..14..226E. doi : 10.1186/s12862-014-0226-8 . PMC 4266906 . PMID 25427971.
- ^ Griffith OW, Blackburn DG, Brandley MC, Van Dyke JU, Whittington CM, Thompson MB (сентябрь 2015 г.). «Реконструкции предкового состояния требуют биологических доказательств для проверки эволюционных гипотез: исследование случая, изучающего эволюцию репродуктивного режима у чешуйчатых рептилий». Журнал экспериментальной зоологии. Часть B, Молекулярная и эволюционная эволюция . 324 (6): 493–503. Bibcode : 2015JEZB..324..493G. doi : 10.1002/jez.b.22614. PMID 25732809.
- ^ Erkenbrack EM, Ako-Asare K, Miller E, Tekelenburg S, Thompson JR, Romano L (январь 2016 г.). «Реконструкция предкового состояния с помощью сравнительного анализа ядра GRN, работающего у иглокожих». Development Genes and Evolution . 226 (1): 37–45. doi :10.1007/s00427-015-0527-y. PMID 26781941. S2CID 6067524.
- ^ Erkenbrack EM, Thompson JR (2019). «Филогенетика типов клеток информирует об эволюционном происхождении идентичности скелетогенных клеток личинок иглокожих». Communications Biology . 2 : 160. doi : 10.1038/s42003-019-0417-3 . PMC 6499829. PMID 31069269.
- ^ ab Chang BS, Ugalde JA, Matz MV (2005). "Применение реконструкции предковых белков в понимании функции белков: GFP-подобные белки". Молекулярная эволюция: получение биохимических данных . Методы в энзимологии. Т. 395. С. 652–670. doi :10.1016/S0076-6879(05)95034-9. ISBN 9780121828004. PMID 15865989.
- ^ Hodges WL (ноябрь 2004 г.). «Эволюция живорождения у рогатых ящериц (Phrynosoma): проверка гипотезы холодного климата». Журнал эволюционной биологии . 17 (6): 1230–1237. doi :10.1111/j.1420-9101.2004.00770.x. PMID 15525408. S2CID 25069395.
- ^ Maddison WP (1991). «Реконструкции предковых состояний с помощью квадратичного изменения для непрерывно-значных признаков на филогенетическом дереве». Systematic Biology . 40 (3): 304–314. doi :10.1093/sysbio/40.3.304.
- ^ Bonine KE, Gleeson TT, Garland T (декабрь 2005 г.). «Изменение типа мышечного волокна у ящериц (Squamata) и филогенетическая реконструкция предполагаемых предковых состояний». Журнал экспериментальной биологии . 208 (Pt 23): 4529–4547. doi :10.1242/jeb.01903. PMID 16339872.
- ^ Ридли М. (1983). Объяснение органического разнообразия: сравнительный метод и адаптации для спаривания . Оксфорд: Clarendon Press.
- ^ Maddison WP (май 1990 г.). «Метод проверки коррелированной эволюции двух бинарных признаков: сосредоточены ли приобретения или потери на определенных ветвях филогенетического дерева?». Эволюция; Международный журнал органической эволюции . 44 (3): 539–557. doi :10.2307/2409434. JSTOR 2409434. PMID 28567979.
- ^ Göbel U, Sander C, Schneider R, Valencia A (апрель 1994 г.). «Коррелированные мутации и контакты остатков в белках». Proteins . 18 (4): 309–317. doi :10.1002/prot.340180402. PMID 8208723. S2CID 14978727.
- ^ Шиндялов ИН, Колчанов NA, Сандер С (март 1994). «Можно ли предсказать трехмерные контакты в белковых структурах с помощью анализа коррелированных мутаций?». Protein Engineering . 7 (3): 349–358. doi :10.1093/protein/7.3.349. PMID 8177884.
- ^ Korber BT, Farber RM, Wolpert DH, Lapedes AS (август 1993 г.). «Ковариация мутаций в петле V3 белка оболочки вируса иммунодефицита человека типа 1: информационный теоретический анализ». Труды Национальной академии наук Соединенных Штатов Америки . 90 (15): 7176–7180. Bibcode : 1993PNAS...90.7176K. doi : 10.1073 /pnas.90.15.7176 . PMC 47099. PMID 8346232.
- ^ Шапиро Б., Рамбо А., Пибус О.Г., Холмс Э.К. (сентябрь 2006 г.). «Филогенетический метод обнаружения положительного эпистаза в последовательностях генов и его применение к эволюции РНК-вирусов» (PDF) . Молекулярная биология и эволюция . 23 (9): 1724–1730. doi : 10.1093/molbev/msl037 . PMID 16774976.
- ^ Poon AF, Lewis FI, Pond SL, Frost SD (ноябрь 2007 г.). «Модель эволюционной сети выявляет стратифицированные взаимодействия в петле V3 оболочки ВИЧ-1». PLOS Computational Biology . 3 (11): e231. Bibcode : 2007PLSCB...3..231P. doi : 10.1371/journal.pcbi.0030231 . PMC 2082504. PMID 18039027 .
- ^ Jermann TM, Opitz JG, Stackhouse J, Benner SA (март 1995 г.). «Реконструкция эволюционной истории суперсемейства рибонуклеаз парнокопытных». Nature . 374 (6517): 57–59. Bibcode :1995Natur.374...57J. doi :10.1038/374057a0. PMID 7532788. S2CID 4315312.
- ^ Садки М., де Альба Э., Перес-Хименес Р., Санчес-Руис Х. М., Муньос В. (март 2009 г.). «Спроектированный белок как экспериментальная модель первичной укладки». Труды Национальной академии наук Соединенных Штатов Америки . 106 (11): 4127–4132. Bibcode : 2009PNAS..106.4127S. doi : 10.1073/pnas.0812108106 . PMC 2647338. PMID 19240216 .
- ^ Chang BS, Jönsson K, Kazmi MA, Donoghue MJ, Sakmar TP (сентябрь 2002 г.). «Воссоздание функционального зрительного пигмента предкового архозавров». Молекулярная биология и эволюция . 19 (9): 1483–1489. doi : 10.1093/oxfordjournals.molbev.a004211 . PMID 12200476.
- ^ Zhang C, Zhang M, Ju J, Nietfeldt J, Wise J, Terry PM и др. (сентябрь 2003 г.). «Геномная диверсификация в филогенетических линиях I и II Listeria monocytogenes: идентификация сегментов, уникальных для популяций линии II». Журнал бактериологии . 185 (18): 5573–5584. doi :10.1128/JB.185.18.5573-5584.2003. PMC 193770. PMID 12949110 .
- ^ Кришнан Н. М., Селигманн Х., Стюарт К. Б., Де Конинг А. П., Поллок Д. Д. (октябрь 2004 г.). «Реконструкция предковой последовательности в митохондриальной ДНК приматов: композиционное смещение и влияние на функциональный вывод». Молекулярная биология и эволюция . 21 (10): 1871–1883. doi : 10.1093/molbev/msh198 . PMID 15229290.
- ^ Гашен Б., Тейлор Дж., Юсим К., Фоли Б., Гао Ф., Ланг Д. и др. (июнь 2002 г.). «Учет разнообразия при выборе вакцины против ВИЧ-1». Science . 296 (5577): 2354–2360. Bibcode :2002Sci...296.2354G. doi :10.1126/science.1070441. PMID 12089434. S2CID 39452987.
- ^ Ролланд М., Дженсен МА., Никл Д.К., Ян Дж., Лёрн Г.Х., Хит Л. и др. (август 2007 г.). «Реконструкция и функция белков предкового центра дерева вируса иммунодефицита человека типа 1». Журнал вирусологии . 81 (16): 8507–8514. doi :10.1128/JVI.02683-06. PMC 1951385. PMID 17537854 .
- ^ Kothe DL, Li Y, Decker JM, Bibollet-Ruche F, Zammit KP, Salazar MG и др. (сентябрь 2006 г.). «Предковые и консенсусные оболочечные иммуногены для ВИЧ-1 подтипа C». Вирусология . 352 (2): 438–449. doi : 10.1016/j.virol.2006.05.011 . PMID 16780913.
- ^ Doria-Rose NA, Learn GH , Rodrigo AG, Nickle DC, Li F, Mahalanabis M и др. (сентябрь 2005 г.). «Предковый белок оболочки вируса иммунодефицита человека типа 1 подтипа B функционален и вызывает нейтрализующие антитела у кроликов, аналогичные тем, которые вызывает циркулирующая оболочка подтипа B». Journal of Virology . 79 (17): 11214–11224. doi :10.1128/JVI.79.17.11214-11224.2005. PMC 1193599. PMID 16103173 .
- ^ McCloskey RM, Liang RH, Harrigan PR, Brumme ZL, Poon AF (июнь 2014 г.). «Оценка филогенетических методов реконструкции переданных вариантов ВИЧ с использованием данных продольной клональной последовательности ВИЧ». Журнал вирусологии . 88 (11): 6181–6194. doi :10.1128/JVI.00483-14. PMC 4093844. PMID 24648453 .
- ^ Бурк Г., Певзнер ПА (январь 2002 г.). «Эволюция в масштабе генома: реконструкция порядков генов у предковых видов». Genome Research . 12 (1): 26–36. PMC 155248. PMID 11779828 .
- ^ Even S, Goldreich O (1981). «Проблема последовательности генератора минимальной длины является NP-трудной». Журнал алгоритмов . 2 (3): 311–313. doi :10.1016/0196-6774(81)90029-8. ISSN 0196-6774.
- ^ Фертин Г., Лабарр А., Русу И., Виалетт С., Таннье Э. (2009). Комбинаторика перестроек генома. МТИ Пресс. doi : 10.7551/mitpress/9780262062824.001.0001. ISBN 9780262258753.
- ^ Wienberg J (декабрь 2004 г.). «Эволюция хромосом эутериан». Current Opinion in Genetics & Development . 14 (6): 657–666. doi :10.1016/j.gde.2004.10.001. PMID 15531161.
- ^ Froenicke L, Caldés MG, Graphodatsky A, Müller S, Lyons LA, Robinson TJ, et al. (март 2006 г.). «Предлагают ли молекулярная цитогенетика и биоинформатика расходящиеся модели предковых геномов млекопитающих?». Genome Research . 16 (3): 306–310. doi :10.1101/gr.3955206. PMC 1415215. PMID 16510895 .
- ^ Murphy WJ, Larkin DM, Everts-van der Wind A, Bourque G, Tesler G, Auvil L, et al. (Июль 2005). «Динамика эволюции хромосом млекопитающих, выведенная из многовидовых сравнительных карт». Science . 309 (5734): 613–617. Bibcode :2005Sci...309..613M. doi :10.1126/science.1111387. PMID 16040707. S2CID 32314883.
- ^ Ma J, Zhang L, Suh BB, Raney BJ, Burhans RC, Kent WJ и др. (декабрь 2006 г.). «Реконструкция смежных областей предкового генома». Genome Research . 16 (12): 1557–1565. doi :10.1101/gr.5383506. PMC 1665639 . PMID 16983148.
- ^ Oyserman BO, Moya F, Lawson CE, Garcia AL, Vogt M, Heffernen M и др. (декабрь 2016 г.). «Реконструкция предкового генома выявляет эволюционную основу приобретения признаков у бактерий, накапливающих полифосфат». Журнал ISME . 10 (12): 2931–2945. Bibcode : 2016ISMEJ..10.2931O. doi : 10.1038/ismej.2016.67. PMC 5148189. PMID 27128993.
- ^ abc Clark JR, Ree RH, Alfaro ME, King MG, Wagner WL, Roalson EH (октябрь 2008 г.). «Сравнительное исследование методов реконструкции ареала предков: прослеживание неопределенных историй островных линий». Systematic Biology . 57 (5): 693–707. doi : 10.1080/10635150802426473 . PMID 18853357.
- ^ Huelsenbeck JP, Nielsen R, Bollback JP (апрель 2003 г.). «Стохастическое отображение морфологических признаков». Systematic Biology . 52 (2): 131–158. CiteSeerX 10.1.1.386.9241 . doi : 10.1080/10635150390192780 . PMID 12746144.
- ^ Ronquist F (1996). "DIVA версия 1.1".
Компьютерная программа и руководство доступны на анонимном FTP из Uppsala University
[ постоянная мертвая ссылка ] - ^ Ree RH, Moore BR, Webb CO, Donoghue MJ (ноябрь 2005 г.). «Структура вероятности для вывода эволюции географического ареала на филогенетических деревьях». Эволюция; Международный журнал органической эволюции . 59 (11): 2299–2311. doi : 10.1111/j.0014-3820.2005.tb00940.x . PMID 16396171. S2CID 23245573.
- ^ abc Lemmon AR, Lemmon EM (август 2008 г.). «Структура правдоподобия для оценки филогеографической истории на непрерывном ландшафте». Systematic Biology . 57 (4): 544–561. CiteSeerX 10.1.1.585.7211 . doi : 10.1080/10635150802304761 . PMID 18686193.
- ^ ab Sturtevant AH, Dobzhansky T (июль 1936 г.). «Инверсии в третьей хромосоме диких рас Drosophila Pseudoobscura и их использование в изучении истории вида». Труды Национальной академии наук Соединенных Штатов Америки . 22 (7): 448–450. Bibcode :1936PNAS...22..448S. doi : 10.1073/pnas.22.7.448 . PMC 1076803 . PMID 16577723.
- ^ ab Campbell L (1998). Историческая лингвистика: введение . Эдинбург: Издательство Эдинбургского университета.
- ^ Yang Z (август 2007 г.). «PAML 4: филогенетический анализ по максимальному правдоподобию». Молекулярная биология и эволюция . 24 (8): 1586–1591. CiteSeerX 10.1.1.322.1650 . doi :10.1093/molbev/msm088. PMID 17483113.
- ^ "Lazarus: программный инструмент для реконструкции последовательностей предковых белков". markov.uoregon.edu . Архивировано из оригинала 2015-03-07 . Получено 2019-03-07 .
- ^ Pond SL, Frost SD, Muse SV (март 2005 г.). «HyPhy: проверка гипотез с использованием филогений». Биоинформатика . 21 (5): 676–679. doi : 10.1093/bioinformatics/bti079 . PMID 15509596.
- ^ Maddison WP, Maddison DR (2015). «Mesquite: модульная система для эволюционного анализа. Версия 2.75».
- ^ ab Tamura K, Stecher G, Peterson D, Filipski A, Kumar S (декабрь 2013 г.). "MEGA6: Molecular Evolutionary Genetics Analysis version 6.0". Молекулярная биология и эволюция . 30 (12): 2725–2729. doi :10.1093/molbev/mst197. PMC 3840312. PMID 24132122 .
- ^ Ronquist F, Huelsenbeck JP (август 2003 г.). «MrBayes 3: байесовский филогенетический вывод в смешанных моделях». Биоинформатика . 19 (12): 1572–1574. doi : 10.1093/bioinformatics/btg180 . PMID 12912839.
- ^ Hubisz MJ, Pollard KS, Siepel A (январь 2011 г.). «PHAST и RPHAST: филогенетический анализ с моделями пространства/времени». Briefings in Bioinformatics . 12 (1): 41–51. doi : 10.1093/bib/bbq072. PMC 3030812. PMID 21278375.
- ^ Bollback JP (февраль 2006 г.). "SIMMAP: стохастическое картирование дискретных признаков в филогениях". BMC Bioinformatics . 7 (1): 88. doi : 10.1186/1471-2105-7-88 . PMC 1403802 . PMID 16504105.
- ^ Парадис Э. (2012). Анализ филогенетики и эволюции с R. Нью-Йорк: Springer-Verlag.
- ^ Росснес Р., Эйдхаммер И., Либерлес Д. А. (май 2005 г.). «Филогенетическая реконструкция состояний предковых признаков для данных по экспрессии генов и сплайсингу мРНК». BMC Bioinformatics . 6 (1): 127. doi : 10.1186/1471-2105-6-127 . PMC 1166541 . PMID 15921519.
- ^ Drummond AJ, Suchard MA, Xie D, Rambaut A (август 2012 г.). «Байесовская филогенетика с BEAUti и BEAST 1.7». Молекулярная биология и эволюция . 29 (8): 1969–1973. doi :10.1093/molbev/mss075. PMC 3408070. PMID 22367748 .
- ^ FitzJohn RG (2012). «Diversitree: сравнительный филогенетический анализ диверсификации в R». Методы в экологии и эволюции . 3 (6): 1084–1092. Bibcode :2012MEcEv...3.1084F. doi :10.1111/j.2041-210X.2012.00234.x. ISSN 2041-210X. S2CID 82351808.
- ^ Pagel M (1994). «Обнаружение коррелированной эволюции в филогениях: общий метод сравнительного анализа дискретных признаков». Труды Королевского общества B: Биологические науки . 255 (1342): 37–45. Bibcode : 1994RSPSB.255...37P. doi : 10.1098/rspb.1994.0006. ISSN 0962-8452. S2CID 85903564.
- ^ Yu Y, Harris AJ, He X (август 2010 г.). "S-DIVA (статистический анализ дисперсии-викарианса): инструмент для вывода биогеографических историй". Молекулярная филогенетика и эволюция . 56 (2): 848–850. Bibcode :2010MolPE..56..848Y. doi :10.1016/j.ympev.2010.04.011. PMID 20399277. S2CID 44980641.
- ^ Ариас JS, Шумик CA, Голобофф PA (декабрь 2011 г.). «Пространственный анализ викариантности: метод использования прямой географической информации в исторической биогеографии». Cladistics . 27 (6): 617–628. doi :10.1111/j.1096-0031.2011.00353.x. hdl : 11336/70196 . PMID 34875812. S2CID 85747431.
- ^ Jones BR, Rajaraman A, Tannier E, Chauve C (сентябрь 2012 г.). «ANGES: реконструкция карт ANcestral GEnomeS». Биоинформатика . 28 (18): 2388–2390. doi : 10.1093/bioinformatics/bts457 . PMID 22820205.
- ^ Ларджет Б., Кадане Дж. Б., Саймон Д. Л. (август 2005 г.). «Байесовский подход к оценке предковых геномных схем». Молекулярная филогенетика и эволюция . 36 (2): 214–223. Bibcode : 2005MolPE..36..214L. doi : 10.1016/j.ympev.2005.03.026. PMID 15893477.
- ^ Csurös M (август 2010). «Подсчет: эволюционный анализ филогенетических профилей с экономией и правдоподобием». Биоинформатика . 26 (15): 1910–1912. doi : 10.1093/bioinformatics/btq315 . PMID 20551134.
- ^ Carmel L, Wolf YI, Rogozin IB, Koonin EV (2010). "EREM: Оценка параметров и предковая реконструкция с помощью алгоритма максимизации ожиданий для вероятностной модели эволюции бинарных геномных признаков". Advances in Bioinformatics . 2010 : 167408. doi : 10.1155/2010/167408 . PMC 2866244 . PMID 20467467.
- ^ Patro R, Sefer E, Malin J, Marçais G, Navlakha S, Kingsford C (сентябрь 2012 г.). "Экономная реконструкция эволюции сетей". Алгоритмы для молекулярной биологии . 7 (1): 25. doi : 10.1186/1748-7188-7-25 . PMC 3492119. PMID 22992218 .
- ^ Diallo AB, Makarenkov V, Blanchette M (январь 2010 г.). «Ancestors 1.0: веб-сервер для реконструкции предковых последовательностей». Bioinformatics . 26 (1): 130–131. doi : 10.1093/bioinformatics/btp600 . PMID 19850756.
- ^ Ashkenazy H, Penn O, Doron-Faigenboim A, Cohen O, Cannarozzi G, Zomer O, Pupko T (июль 2012 г.). "FastML: веб-сервер для вероятностной реконструкции предковых последовательностей". Nucleic Acids Research . 40 (выпуск веб-сервера): W580–W584. doi :10.1093/nar/gks498. PMC 3394241. PMID 22661579 .
- ^ Hu F, Lin Y, Tang J (ноябрь 2014 г.). "MLGO: реконструкция филогении и вывод предков из данных о порядке генов". BMC Bioinformatics . 15 (1): 354. doi : 10.1186/s12859-014-0354-6 . PMC 4236499. PMID 25376663 .
- ^ Bouchard-Côté A, Jordan MI (январь 2013 г.). «Эволюционный вывод через процесс Пуассона-Инделя». Труды Национальной академии наук Соединенных Штатов Америки . 110 (4): 1160–1166. arXiv : 1207.6327 . Bibcode : 2013PNAS..110.1160B. doi : 10.1073/pnas.1220450110 . PMC 3557041. PMID 23275296 .
- ^ Thorne JL, Kishino H, Felsenstein J (август 1991 г.). «Эволюционная модель для выравнивания последовательностей ДНК с максимальным правдоподобием». Journal of Molecular Evolution . 33 (2): 114–124. Bibcode : 1991JMolE..33..114T. doi : 10.1007/BF02193625. PMID 1920447. S2CID 13333056.
- ^ Poon AF, Swenson LC, Bunnik EM, Edo-Matas D, Schuitemaker H, van 't Wout AB , Harrigan PR (2012). «Реконструкция динамики эволюции ВИЧ внутри хозяев на основе данных последовательного глубокого секвенирования». PLOS Computational Biology . 8 (11): e1002753. Bibcode : 2012PLSCB...8E2753P. doi : 10.1371/journal.pcbi.1002753 . PMC 3486858. PMID 23133358 .
- ^ Schwarz RF , Trinh A, Sipos B, Brenton JD, Goldman N, Markowetz F (апрель 2014 г.). "Филогенетическая количественная оценка внутриопухолевой гетерогенности". PLOS Computational Biology . 10 (4): e1003535. arXiv : 1306.1685 . Bibcode : 2014PLSCB..10E3535S. doi : 10.1371/journal.pcbi.1003535 . PMC 3990475. PMID 24743184 .