Взвешенная сеть
Сеть, в которой связи между узлами имеют назначенные им веса

Взвешенная сеть — это сеть , в которой связи между узлами имеют назначенные им веса. Сеть — это система, элементы которой каким-то образом связаны. [1] Элементы системы представлены в виде узлов (также известных как субъекты или вершины), а связи между взаимодействующими элементами известны как связи, ребра, дуги или ссылки. Узлами могут быть нейроны, отдельные лица, группы, организации, аэропорты или даже страны, тогда как связи могут принимать форму дружбы, общения, сотрудничества, альянса, потока или торговли, и это лишь некоторые из них.

В ряде реальных сетей не все связи в сети имеют одинаковую емкость. Фактически, связи часто связаны с весами, которые различают их по их силе, интенсивности или емкости [2] [3] С одной стороны, Марк Грановеттер (1973) [4] утверждал, что сила социальных отношений в социальных сетях является функцией их продолжительности, эмоциональной интенсивности, близости и обмена услугами. С другой стороны, для несоциальных сетей веса часто относятся к функции, выполняемой связями, например, поток углерода (мг/м 2 /день) между видами в пищевых сетях , [5] количество синапсов и щелевых соединений в нейронных сетях, [6] или объем трафика, текущего по соединениям в транспортных сетях. [7]

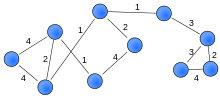
Пример взвешенной сети (веса также можно визуализировать, задавая ребрам разную ширину)

Регистрируя силу связей [8], можно создать взвешенную сеть (также известную как ценностная сеть).

Взвешенные сети также широко используются в геномных и системных биологических приложениях. [3] Например, взвешенный анализ сети коэкспрессии генов (WGCNA) часто используется для построения взвешенной сети среди генов (или продуктов генов) на основе данных экспрессии генов (например, микрочипов ). [9] В более общем плане, взвешенные корреляционные сети могут быть определены путем мягкого порогового значения парных корреляций между переменными (например, измерениями генов). [10]

Меры для взвешенных сетей

Хотя взвешенные сети сложнее анализировать, чем если бы связи просто присутствовали или отсутствовали, для взвешенных сетей был предложен ряд сетевых показателей:

  • Сила узла: сумма весов, прикрепленных к связям, принадлежащим узлу [2]
  • Близость : переопределено с использованием алгоритма расстояния Дейкстры [11]
  • Посредничество : переопределено с использованием алгоритма расстояния Дейкстры [12] [13]
  • Коэффициент кластеризации (глобальный): переопределен с использованием триплетного значения [14]
  • Коэффициент кластеризации (локальный): переопределяется с использованием триплетного значения [2] или с использованием алгебраической формулы [9]

Теоретическое преимущество взвешенных сетей заключается в том, что они позволяют выводить отношения между различными сетевыми мерами (также известными как сетевые концепции, статистики или индексы). [3] Например, Донг и Хорват (2007) [15] показывают, что простые отношения между сетевыми мерами могут быть выведены в кластерах узлов (модулей) во взвешенных сетях. Для взвешенных корреляционных сетей можно использовать угловую интерпретацию корреляций, чтобы обеспечить геометрическую интерпретацию сетевых теоретических концепций и вывести неожиданные отношения между ними Хорват и Донг (2008) [16]

Внутренне плотные взвешенные сети

В теории сетей внутренне плотные взвешенные сети представляют собой особый класс сложных структур, характеризующихся почти полной полнотой связей и связанных с ними весов, что выходит за рамки обычных ограничений более разреженных сетевых конфигураций. В отличие от разреженных сетей, где отсутствие связей обычно указывает на отсутствие взаимодействия, внутренне плотные сети демонстрируют всеобъемлющую взаимосвязь между узлами, где каждый узел сложным образом связан со всеми остальными. Такие системы не имеют очевидных естественных ограничений для узла, чтобы иметь связь с любым или всеми другими узлами.

Термин «внутренне плотный» подчеркивает, что ребра в этих сетях могут не только представлять положительные отношения, но могут охватывать случайность или даже отрицательные ассоциации на основе их соответствующих весов. Например, в сценариях, где веса ребер обозначают сходство между узлами, более низкие веса не просто означают отсутствие сходства, но могут обозначать несходство или отрицательные базовые связи. Исследование Гурсоя и Бадура (2021) [17] представило методы извлечения значимых и разреженных подписанных остовов из этих сетей, демонстрируя их значимость в сохранении сложных структур, присущих внутренне плотным взвешенным сетям в различных областях, включая определенные сети миграции, голосования, контактов между людьми и совместного проживания видов. Эта отличительная сетевая парадигма расширяет понимание сложных систем, наблюдаемых в естественных, социальных и технологических областях, предлагая понимание тонких взаимодействий и отношений в этих плотно взаимосвязанных сетях.

Программное обеспечение для анализа взвешенных сетей

Существует ряд программных пакетов, которые могут анализировать взвешенные сети; см. программное обеспечение для анализа социальных сетей . Среди них — фирменное программное обеспечение UCINET и пакет с открытым исходным кодом tnet. [18]

Пакет WGCNA R реализует функции для построения и анализа взвешенных сетей в частности взвешенных корреляционных сетей. [10]

Смотрите также

Ссылки

  1. ^ Вассерман, С., Фауст, К., 1994. Анализ социальных сетей: методы и приложения. Cambridge University Press, Нью-Йорк, штат Нью-Йорк.
  2. ^ abc A. Barrat и M. Barthelemy и R. Pastor-Satorras и A. Vespignani (2004). "Архитектура сложных взвешенных сетей". Труды Национальной академии наук . 101 (11): 3747– 3752. arXiv : cond-mat/0311416 . Bibcode :2004PNAS..101.3747B. doi : 10.1073/pnas.0400087101 . PMC  374315 . PMID  15007165.
  3. ^ abc Хорват, С., 2011. Взвешенный сетевой анализ. Приложения в геномике и системной биологии. Springer Book. ISBN 978-1-4419-8818-8 . 
  4. ^ Грановеттер, М. (1973). «Сила слабых связей». Американский журнал социологии . 78 (6): 1360– 1380. doi : 10.1086/225469. S2CID  59578641.
  5. ^ Лучкович, Дж. Дж.; Боргатти, С. П.; Джонсон, Дж. К.; Эверетт, МГ (2003). «Определение и измерение сходства трофических ролей в пищевых сетях с использованием регулярной эквивалентности». Журнал теоретической биологии . 220 (3): 303– 321. Bibcode :2003JThBi.220..303L. CiteSeerX 10.1.1.118.3862 . doi :10.1006/jtbi.2003.3147. PMID  12468282. 
  6. ^ DJ Watts и Steven Strogatz (июнь 1998). "Коллективная динамика сетей 'малого мира'" (PDF) . Nature . 393 (6684): 440– 442. Bibcode :1998Natur.393..440W. doi :10.1038/30918. PMID  9623998. S2CID  4429113. Архивировано из оригинала (PDF) 21.02.2007.
  7. ^ Tore Opsahl и Vittoria Colizza и Pietro Panzarasa и Jose J. Ramasco (2008). "Prominence and control: The weighted rich-club effect". Physical Review Letters . 101 (16): 168702. arXiv : 0804.0417 . Bibcode : 2008PhRvL.101p8702O. doi : 10.1103/PhysRevLett.101.168702. PMID  18999722. S2CID  29349737. Архивировано из оригинала 27.11.2009 . Получено 17.09.2009 .
  8. ^ "Операционализация прочности связей в социальных сетях". 2009-02-06. Архивировано из оригинала 2009-08-24 . Получено 2009-09-17 .
  9. ^ ab Zhang, Bin; Horvath, Steve (2005). "Общая структура для анализа сетей взвешенной коэкспрессии генов". Статистические приложения в генетике и молекулярной биологии . 4 : Статья17. doi :10.2202/1544-6115.1128. PMID  16646834. S2CID  7756201.
  10. ^ ab Лангфельдер, Питер; Хорват, Стив (2008). "WGCNA: пакет R для анализа сетей с весовой корреляцией". BMC Bioinformatics . 9 : 559. doi : 10.1186/1471-2105-9-559 . PMC 2631488. PMID  19114008 .  Значок открытого доступа
  11. ^ Newman, Mark EJ (2001). "Сети научного сотрудничества: II. Кратчайшие пути, взвешенные сети и центральность" (PDF) . Physical Review E . 64 (1): 016132. arXiv : cond-mat/0011144 . Bibcode :2001PhRvE..64a6132N. doi :10.1103/PhysRevE.64.016132. PMID  11461356. S2CID  12985167. Архивировано (PDF) из оригинала 2008-10-10 . Получено 2009-09-17 .
  12. ^ Брандес, У (2008). «О вариантах центральности кратчайшего пути и их общем вычислении». Социальные сети . 30 (2): 136–145 . CiteSeerX 10.1.1.72.9610 . doi :10.1016/j.socnet.2007.11.001. 
  13. ^ Opsahl, T; Agneessens, F; Skvoretz, J (2010). «Центральность узлов во взвешенных сетях: обобщение степени и кратчайших путей». Социальные сети . 32 (3): 245– 251. doi : 10.1016/j.socnet.2010.03.006. Архивировано из оригинала 24 июня 2021 г. Получено 17 июня 2021 г.
  14. ^ Tore Opsahl; Pietro Panzarasa (2009). «Кластеризация во взвешенных сетях». Социальные сети . 31 (2): 155– 163. CiteSeerX 10.1.1.180.9968 . doi :10.1016/j.socnet.2009.02.002. S2CID  8822670. Архивировано из оригинала 01.07.2019 . Получено 17.09.2009 . 
  15. ^ Донг Дж, Хорват С (2007) «Понимание сетевых концепций в модулях». BMC Systems Biology 2007, июнь 1:24Значок открытого доступа
  16. ^ Донг, Джун; Хорват, Стив (2008). Мияно, Сатору (ред.). "Геометрическая интерпретация анализа сетей коэкспрессии генов". PLOS Computational Biology . 4 (8): e1000117. Bibcode : 2008PLSCB ...4E0117H. doi : 10.1371/journal.pcbi.1000117 . PMC 2446438. PMID  18704157.  Значок открытого доступа
  17. ^ Гурсой, Фуркан; Бадур, Бертан (18.09.2021). «Извлечение подписанного остова внутренне плотных взвешенных сетей». Журнал сложных сетей . 9 (5). arXiv : 2012.05216 . doi : 10.1093/comnet/cnab019. ISSN  2051-1310.
  18. ^ "tnet » Software". Tore Opsahl. 12 июня 2011 г. Архивировано из оригинала 15 июня 2021 г. Получено 17 июня 2021 г.
Получено с "https://en.wikipedia.org/w/index.php?title=Weighted_network&oldid=1272728017"