Элементарная ячейка

Повторяющаяся единица, образованная векторами, охватывающими точки решетки

В геометрии , биологии , минералогии и физике твердого тела элементарная ячейка — это повторяющаяся единица, образованная векторами, охватывающими точки решетки. ^[1] Несмотря на свое многозначительное название, элементарная ячейка (в отличие, например, от единичного вектора) не обязательно имеет единичный размер или даже какой-либо определенный размер. Скорее, примитивная ячейка является ближайшей аналогией единичного вектора, поскольку она имеет определенный размер для данной решетки и является основным строительным блоком, из которого строятся более крупные ячейки.

Эта концепция используется, в частности, при описании кристаллической структуры в двух и трех измерениях, хотя она имеет смысл во всех измерениях. Решетка может быть охарактеризована геометрией ее элементарной ячейки, которая является сечением мозаики ( параллелограмма или параллелепипеда ), которое генерирует всю мозаику, используя только трансляции.

Существует два особых случая элементарной ячейки: примитивная ячейка и условная ячейка . Примитивная ячейка — это элементарная ячейка, соответствующая одной точке решетки , это наименьшая возможная элементарная ячейка. ^[2] В некоторых случаях полная симметрия кристаллической структуры не очевидна из примитивной ячейки, в таких случаях может использоваться условная ячейка. Обычная ячейка (которая может быть или не быть примитивной) — это элементарная ячейка с полной симметрией решетки и может включать более одной точки решетки. Обычные элементарные ячейки — это параллелотопы в n измерениях.

Примитивная клетка

Примитивная ячейка — это ячейка, которая содержит ровно одну точку решетки. Для ячеек, как правило, точки решетки, которые являются общими для $n$ ячеек, считаются ⁠1/ $н$ ⁠ точек решетки, содержащихся в каждой из этих ячеек; так, например, примитивная элементарная ячейка в трех измерениях, которая имеет точки решетки только в своих восьми вершинах, считается содержащей ⁠1/8⁠ каждого из них. ^[3] Альтернативная концептуализация заключается в последовательном выборе только одной из $n$ точек решетки, принадлежащей данной элементарной ячейке (так, чтобы остальные $n-1$ точек решетки принадлежали соседним элементарным ячейкам).

Векторы примитивного трансляции $a \to 1$ , $a \to 2$ , $a \to 3$ охватывают ячейку решетки наименьшего объема для конкретной трехмерной решетки и используются для определения вектора трансляции кристалла.

{\vec {T}}=u_{1}{\vec {a}}_{1}+u_{2}{\vec {a}}_{2}+u_{3}{\vec {a}}_{3},

где $u 1$ , $u 2$ , $u 3$ — целые числа, трансляция которых оставляет решетку инвариантной. ^{[примечание 1]} То есть, для точки в решетке $r$ расположение точек выглядит таким же из $r' = r + T \to ,$ как и из $r$ . ^[4]

Поскольку примитивная ячейка определяется примитивными осями (векторами) $a \to 1$ , $a \to 2$ , $a \to 3$ , объем $V p$ примитивной ячейки определяется параллелепипедом из вышеуказанных осей как

V_{\mathrm {p} }=\left|{\vec {a}}_{1}\cdot ({\vec {a}}_{2}\times {\vec {a}}_{3})\right|.

Обычно примитивные ячейки в двух и трех измерениях выбираются в форме параллелограммов и параллелепипедов, с атомом в каждом углу ячейки. Этот выбор примитивной ячейки не является уникальным, но объем примитивных ячеек всегда будет задаваться выражением выше. ^[5]

Ячейка Вигнера-Зейтца

В дополнение к примитивным ячейкам в виде параллелепипеда, для каждой решетки Бравэ существует другой тип примитивной ячейки, называемый ячейкой Вигнера–Зейтца. В ячейке Вигнера–Зейтца точка решетки находится в центре ячейки, и для большинства решеток Бравэ форма не является параллелограммом или параллелепипедом. Это тип ячейки Вороного . Ячейка Вигнера–Зейтца обратной решетки в импульсном пространстве называется зоной Бриллюэна .

Обычная ячейка

Для каждой конкретной решетки кристаллографы выбирали условную ячейку в каждом конкретном случае на основе удобства расчета. ^[6] Эти условные ячейки могут иметь дополнительные точки решетки, расположенные в середине граней или тела элементарной ячейки. Количество точек решетки, а также объем условной ячейки являются целым кратным (1, 2, 3 или 4) объема примитивной ячейки. ^[7]

Два измерения

Для любой двумерной решетки элементарные ячейки являются параллелограммами , которые в особых случаях могут иметь ортогональные углы, равные длины или и то, и другое. Четыре из пяти двумерных решеток Браве представлены с использованием обычных примитивных ячеек, как показано ниже.

Обычная примитивная клетка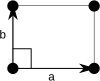
Имя формы	Параллелограмм	Прямоугольник	Квадрат	Ромб
решетка Бравэ	Примитивный косой	Примитивный Прямоугольный	Примитивный квадрат	Примитивный шестиугольный

Центрированная прямоугольная решетка также имеет примитивную ячейку в форме ромба, но для того, чтобы обеспечить легкое различение на основе симметрии, она представлена обычной ячейкой, содержащей две точки решетки.

Примитивная клетка
Имя формы	Ромб
Обычная ячейка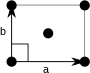
решетка Бравэ	Прямоугольный по центру

Три измерения

Для любой трехмерной решетки обычные элементарные ячейки — это параллелепипеды , которые в особых случаях могут иметь ортогональные углы, или равные длины, или и то, и другое. Семь из четырнадцати трехмерных решеток Браве представлены с использованием обычных примитивных ячеек, как показано ниже.

Обычная примитивная клетка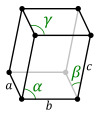
Имя формы	Параллелепипед	Наклонная прямоугольная призма	Прямоугольный кубоид	Квадратный кубоид	Треугольный трапецоэдр	Куб	Прямая ромбическая призма
решетка Бравэ	Примитивный триклинный	Примитивная моноклинная	Примитивный орторомбический	Примитивный Тетрагональный	Примитивный ромбоэдрический	Примитивный кубический	Примитивный шестиугольный

Остальные семь решеток Браве (известные как центрированные решетки) также имеют примитивные ячейки в форме параллелепипеда, но для того, чтобы обеспечить легкую дискриминацию на основе симметрии, они представлены обычными ячейками, которые содержат более одной точки решетки.

Примитивная клетка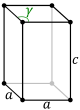
Имя формы	Наклонная ромбическая призма	Прямая ромбическая призма
Обычная ячейка
решетка Бравэ	Моноклинная с центром на основании	Орторомбическая с центром на основании	Объемно-центрированная орторомбическая	Гранецентрированная орторомбическая	Тетрагональный объемно-центрированный	Объемно-центрированная кубическая	Гранецентрированный кубический

Смотрите также

Примечания

^ В $n$ измерениях вектор трансляции кристалла будет
${\vec {T}}=\sum _{i=1}^{n}u_{i}{\vec {a}}_{i},\quad {\mbox{where }}u_{i}\in \mathbb {Z} \quad \forall i.$
То есть для точки в решетке $r$ расположение точек выглядит таким же из $r' = r + T \to ,$ как и из $r$ .

Ссылки

^ Эшкрофт, Нил В. (1976). "Глава 4". Физика твердого тела . WB Saunders Company. стр. 72. ISBN 0-03-083993-9.
^ Саймон, Стивен (2013). Оксфордская физика твердого тела (1-е изд.). Oxford University Press. стр. 114. ISBN 978-0-19-968076-4.
^ "DoITPoMS – TLP Library Crystallography – Unit Cell". Онлайн-ресурсы для изучения материаловедения: DoITPoMS . Кембриджский университет . Получено 21 февраля 2015 г.
^ Киттель, Чарльз (11 ноября 2004 г.). Введение в физику твердого тела (8-е изд.). Wiley. стр. 4. ISBN 978-0-471-41526-8.
^ Mehl, Michael J.; Hicks, David; Toher, Cormac; Levy, Ohad; Hanson, Robert M.; Hart, Gus; Curtarolo, Stefano (2017). «Библиотека кристаллографических прототипов AFLOW: Часть 1». Computational Materials Science . 136 . Elsevier BV: S1 – S828 . arXiv : 1806.07864 . doi :10.1016/j.commatsci.2017.01.017. ISSN 0927-0256. S2CID 119490841.
^ Аройо, MI, ред. (2016-12-31). Международные таблицы по кристаллографии . Честер, Англия: Международный союз кристаллографии. стр. 25. doi :10.1107/97809553602060000114. ISBN 978-0-470-97423-0.
^ Эшкрофт, Нил В. (1976). Физика твердого тела . WB Saunders Company. стр. 73. ISBN 0-03-083993-9.

[first-4] В $n$ измерениях вектор трансляции кристалла будет
${\vec {T}}=\sum _{i=1}^{n}u_{i}{\vec {a}}_{i},\quad {\mbox{where }}u_{i}\in \mathbb {Z} \quad \forall i.$
То есть для точки в решетке $r$ расположение точек выглядит таким же из $r' = r + T \to ,$ как и из $r$ .

[1] Эшкрофт, Нил В. (1976). "Глава 4". Физика твердого тела . WB Saunders Company. стр. 72. ISBN 0-03-083993-9.

[2] Саймон, Стивен (2013). Оксфордская физика твердого тела (1-е изд.). Oxford University Press. стр. 114. ISBN 978-0-19-968076-4.

[doitpoms-3] "DoITPoMS – TLP Library Crystallography – Unit Cell". Онлайн-ресурсы для изучения материаловедения: DoITPoMS . Кембриджский университет . Получено 21 февраля 2015 г.

[5] Киттель, Чарльз (11 ноября 2004 г.). Введение в физику твердого тела (8-е изд.). Wiley. стр. 4. ISBN 978-0-471-41526-8.

[6] Mehl, Michael J.; Hicks, David; Toher, Cormac; Levy, Ohad; Hanson, Robert M.; Hart, Gus; Curtarolo, Stefano (2017). «Библиотека кристаллографических прототипов AFLOW: Часть 1». Computational Materials Science . 136 . Elsevier BV: S1 – S828 . arXiv : 1806.07864 . doi :10.1016/j.commatsci.2017.01.017. ISSN 0927-0256. S2CID 119490841.

[7] Аройо, MI, ред. (2016-12-31). Международные таблицы по кристаллографии . Честер, Англия: Международный союз кристаллографии. стр. 25. doi :10.1107/97809553602060000114. ISBN 978-0-470-97423-0.

[8] Эшкрофт, Нил В. (1976). Физика твердого тела . WB Saunders Company. стр. 73. ISBN 0-03-083993-9.