Кубико-октаэдрические соты
| Кубо-октаэдрические соты | |
|---|---|
| Тип | Компактные однородные соты |
| Символ Шлефли | {(3,4,3,4)} или {(4,3,4,3)} |
| Диаграммы Коксетера |             ↔ ↔      ↔ ↔   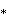 |
| Клетки | {4,3}  {3,4}  г{4,3}  |
| Лица | треугольник {3} квадрат {4} |
| Вершинная фигура |  ромбокубооктаэдр |
| Группа Коксетера | [(4,3) [2] ] |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный |
В геометрии гиперболического 3-пространства кубооктаэдрические соты представляют собой компактные однородные соты , построенные из ячеек куба , октаэдра и кубооктаэдра в вершинной фигуре ромбокубооктаэдра . Они имеют однокольцевую диаграмму Коксетера ,



 , и назван по двум своим обычным ячейкам.
, и назван по двум своим обычным ячейкам.
Геометрические соты — это заполнение пространства многогранными или более многомерными ячейками , так что нет никаких пробелов. Это пример более общей математической мозаики или тесселяции в любом количестве измерений.
Соты обычно строятся в обычном евклидовом («плоском») пространстве, как выпуклые однородные соты . Они также могут быть построены в неевклидовых пространствах , как гиперболические однородные соты . Любой конечный однородный многогранник может быть спроецирован на его описанную сферу , чтобы сформировать однородные соты в сферическом пространстве.
Изображения
Широкоугольные перспективные виды:
- Центрирован на кубе
- В центре октаэдра
- Центрирован на кубооктаэдре
Он содержит подгруппу мозаики H2, чередующуюся шестиугольную мозаику порядка 4 ,

 , с вершинной фигурой (3.4) 4 .
, с вершинной фигурой (3.4) 4 .
Симметрия
Более низкая форма симметрии, индекс 6, этих сот может быть построена с симметрией [(4,3,4,3 * )], представленной фундаментальной областью тригонального трапецоэдра , и диаграммой Кокстера 





 . Эту более низкую симметрию можно расширить, восстановив одно зеркало как
. Эту более низкую симметрию можно расширить, восстановив одно зеркало как



 .
.
   ↔ ↔      = =  |    ↔ ↔      = =  |    ↔ ↔      = =  |
Связанные соты
Существует 5 родственных однородных сот, созданных в пределах одного семейства, образованного с помощью 2 или более колец группы Коксетера.



 :
:



 ,
,



 ,
,



 ,
,



 ,
,



 .
.
Выпрямленные кубо-октаэдрические соты
| Выпрямленные кубо-октаэдрические соты | |
|---|---|
| Тип | Компактные однородные соты |
| Символ Шлефли | г{(4,3,4,3)} |
| Диаграммы Коксетера |      |
| Клетки | г{4,3}  рр{3,4}  |
| Лица | треугольник {3} квадрат {4} |
| Вершинная фигура |  кубоид |
| Группа Коксетера | [[(4,3) [2] ]],     |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный |
Выпрямленные кубооктаэдрические соты — это компактные однородные соты , построенные из ячеек кубооктаэдра и ромбокубооктаэдра , в кубоидной вершинной фигуре . Они имеют диаграмму Кокстера



 .
.
- Перспективный вид из центра ромбокубооктаэдра
Циклоусеченные кубо-октаэдрические соты
| Циклоусеченные кубо-октаэдрические соты | |
|---|---|
| Тип | Компактные однородные соты |
| Символ Шлефли | ct{(4,3,4,3)} |
| Диаграммы Коксетера |      |
| Клетки | т{4,3}  {3,4}  |
| Лица | треугольник {3} восьмиугольник {8} |
| Вершинная фигура |  квадратная антипризма |
| Группа Коксетера | [[(4,3) [2] ]],     |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный |
Циклоусеченные кубооктаэдрические соты — это компактные однородные соты , построенные из усеченных кубических и октаэдрических ячеек, в квадратной антипризменной вершинной фигуре . Они имеют диаграмму Коксетера



 .
.
- Перспективный вид из центра октаэдра
Его можно рассматривать как некий аналог триоктагональной мозаики , которая имеет усеченные квадратные и треугольные грани:
Циклоусеченные октаэдрически-кубические соты
| Циклоусеченные октаэдрически-кубические соты | |
|---|---|
| Тип | Компактные однородные соты |
| Символ Шлефли | ct{(3,4,3,4)} |
| Диаграммы Коксетера |             ↔ ↔      ↔ ↔   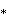 |
| Клетки | {4,3}  т{3,4}  |
| Лица | квадрат {4} шестиугольник {6} |
| Вершинная фигура |  треугольная антипризма |
| Группа Коксетера | [[(4,3) [2] ]],     |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный |
Циклоусеченные октаэдрально-кубические соты — это компактные однородные соты , построенные из кубических и усеченных октаэдрических ячеек, в вершинной фигуре треугольной антипризмы . Они имеют диаграмму Коксетера



 .
.
- Перспективный вид из центра куба
Он содержит тетрагексагональную мозаику подгруппы H2 с чередующимися квадратными и шестиугольными гранями, с диаграммой Коксетера

 или полусимметрия
или полусимметрия

 :
:
Симметрия
 Треугольный трапецоэдр        ↔ ↔   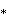 |  Половина домена        ↔ ↔      |  Подгруппа H 2 , ромбическая *3232    ↔ ↔    |
Радиальная подгруппа симметрии, индекс 6, этих сот может быть построена с помощью [(4,3,4,3 * )],


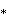 , представленная фундаментальной областью в виде тригонального трапецоэдра , и диаграммой Кокстера
, представленная фундаментальной областью в виде тригонального трапецоэдра , и диаграммой Кокстера 





 . Эту более низкую симметрию можно расширить, восстановив одно зеркало как
. Эту более низкую симметрию можно расширить, восстановив одно зеркало как



 .
.
   ↔ ↔      = =  |    ↔ ↔      = = | |
Усеченные кубо-октаэдрические соты
| Усеченные кубо-октаэдрические соты | |
|---|---|
| Тип | Компактные однородные соты |
| Символ Шлефли | т{(4,3,4,3)} |
| Диаграммы Коксетера |      |
| Клетки | т{3,4}  т{4,3}  рр{3,4}  тр{4,3}  |
| Лица | треугольник {3} квадрат {4} шестиугольник {6} восьмиугольник {8} |
| Вершинная фигура |  прямоугольная пирамида |
| Группа Коксетера | [(4,3) [2] ] |
| Характеристики | Вершинно-транзитивный |
Усеченные кубооктаэдрические соты — это компактные однородные соты , построенные из ячеек усеченного октаэдра , усеченного куба , ромбокубооктаэдра и усеченного кубооктаэдра в вершинной фигуре прямоугольной пирамиды . Они имеют диаграмму Коксетера



 .
.
- Перспективный вид из центра ромбокубооктаэдра
Всеусеченные кубо-октаэдрические соты
| Всеусеченные кубо-октаэдрические соты | |
|---|---|
| Тип | Компактные однородные соты |
| Символ Шлефли | тр{(4,3,4,3)} |
| Диаграммы Коксетера |      |
| Клетки | тр{3,4}  |
| Лица | квадрат {4} шестиугольник {6} восьмиугольник {8} |
| Вершинная фигура |  Ромбический двуклиновидный |
| Группа Коксетера | [2[(4,3) [2] ]] или [(2,2) + [(4,3) [2] ]],     |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный, ячеично-транзитивный |
Всеусеченные кубооктаэдрические соты — это компактные однородные соты , построенные из усеченных кубооктаэдрических ячеек, в ромбической двуклиновидной вершинной фигуре . Они имеют диаграмму Коксетера



 с [2,2] + (порядок 4) расширенной симметрией в его ромбической двуклиновидной вершинной фигуре .
с [2,2] + (порядок 4) расширенной симметрией в его ромбической двуклиновидной вершинной фигуре .
- Перспективный вид из центра усеченного кубооктаэдра
Смотрите также
Ссылки
- Коксетер , Правильные многогранники , 3-е изд., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
- Коксетер , Красота геометрии: Двенадцать эссе , Dover Publications, 1999 ISBN 0-486-40919-8 (Глава 10: Регулярные соты в гиперболическом пространстве, Сводные таблицы II, III, IV, V, стр. 212-213)
- Джеффри Р. Уикс Форма пространства, 2-е издание ISBN 0-8247-0709-5 (Главы 16–17: Геометрии на трехмерных многообразиях I, II)
- Норман Джонсон Однородные многогранники , Рукопись
- NW Johnson : Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 г.
- NW Johnson: Геометрии и преобразования , (2018) Глава 13: Гиперболические группы Коксетера











