Поверхность рода g
В математике поверхность рода g (также известная как g -тор или g -дырчатый тор ) — это поверхность, образованная связной суммой g различных торов : внутренняя часть диска удаляется из каждого из g различных торов, а границы g множества дисков отождествляются (склеиваются), образуя g -тор. Род такой поверхности — g .
Поверхность рода g — это двумерное многообразие . Теорема классификации поверхностей утверждает, что каждое компактное связное двумерное многообразие гомеоморфно либо сфере, либо связной сумме торов, либо связной сумме вещественных проективных плоскостей .
Определение рода
Род связной ориентируемой поверхности — это целое число, представляющее максимальное количество разрезов вдоль непересекающихся замкнутых простых кривых, не делая полученное многообразие несвязным. [1] Он равен количеству ручек на нем. Альтернативно, его можно определить в терминах эйлеровой характеристики χ , через соотношение χ = 2 − 2 g для замкнутых поверхностей , где g — род.
Род (иногда называемый полуродом или родом Эйлера) связной неориентируемой замкнутой поверхности — это положительное целое число, представляющее количество поперечных колпачков, прикрепленных к сфере. Альтернативно, его можно определить для замкнутой поверхности в терминах эйлеровой характеристики χ , через соотношение χ = 2 − g , где g — неориентируемый род.
Род 0
Ориентируемой поверхностью рода ноль является сфера S 2. Другой поверхностью рода ноль является диск .
- Представления поверхностей рода 0
- Сфера
- Замкнутый диск (с границей)
- По гипотезе Хивуда , его можно раскрасить максимум четырьмя смежными областями.
Род 1
Ориентируемая поверхность рода один — это обычный тор. Неориентируемая поверхность рода один — это проективная плоскость . [2]
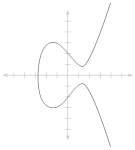
Эллиптические кривые над комплексными числами можно отождествить с поверхностями рода 1. Формулировка эллиптических кривых как вложения тора в комплексную проективную плоскость естественным образом следует из свойства эллиптических функций Вейерштрасса , которое позволяет получать эллиптические кривые из фактора комплексной плоскости по решетке . [3]
- Представления поверхностей рода 1
- Тор рода 1
- Может быть окрашен с использованием до 7 смежных областей.
- Эллиптическая кривая
Род 2
Термин двойной тор иногда используется для обозначения поверхности рода 2. [4] [5] Неориентируемая поверхность рода 2 — это бутылка Клейна .
Поверхность Больца является наиболее симметричной римановой поверхностью рода 2 в том смысле, что она имеет наибольшую возможную группу конформных автоморфизмов . [6]
- Представления поверхностей рода 2
- Тор рода 2
- Может быть окрашен с использованием до 8 смежных областей.
Род 3
Термин тройной тор также иногда используется для обозначения поверхности рода 3. [7] [5]
Квартика Клейна — компактная риманова поверхность рода 3 с группой автоморфизмов максимально возможного порядка для компактных римановых поверхностей рода 3. Она имеет 168 сохраняющих ориентацию автоморфизмов и всего 336 автоморфизмов.
- Несколько поверхностей рода 3
- Шар с тремя ручками
- Тройной тор
- Может быть окрашен с использованием до 9 смежных областей.
- Двенадцатиугольник с противоположными сторонами, обозначенными [8]
- Тетрадекагон с противоположными сторонами, обозначенными [8]
Смотрите также
Ссылки
- ^ Манкрес, Джеймс Р. Топология. Том 2. Верхняя Сэддл-Ривер: Prentice Hall, 2000.
- ^ Бредон, Глен Э. (1993). Топология и геометрия . Springer-Verlag. ISBN 0-387-97926-3.
- ^ Сильверман, Джозеф Х. (1986). Арифметика эллиптических кривых . Graduate Texts in Mathematics. Том 106. Springer-Verlag. ISBN 0-387-96203-4.
- ^ Вайсштейн, Эрик В. «Двойной тор». MathWorld .
- ^ ab Mayorga, Luis S.; Masone, Diego (2024). «Тайный балет внутри многопузырьковых тел». ACS Nano . 18 (24): 15651. doi :10.1021/acsnano.4c01590.
- ^ Больца, Оскар (1887), «О бинарных секстиках с линейными преобразованиями в самих себя», Американский журнал математики , 10 (1): 47–70, doi :10.2307/2369402, JSTOR 2369402
- ^ Вайсштейн, Эрик В. «Тройной тор». MathWorld .
- ^ ab Юрген Йост, (1997) «Компактные римановы поверхности: введение в современную математику», Springer
Источники
- Джеймс Р. Манкрес, Топология, второе издание , Prentice-Hall, 2000, ISBN 0-13-181629-2 .
- Уильям С. Мэсси, Алгебраическая топология: Введение , Харбрейс, 1967.












![Двенадцатиугольник с противоположными сторонами, обозначенными[8]](http://upload.wikimedia.org/wikipedia/commons/thumb/7/73/Dodecagon_with_opposite_faces_identified.svg/150px-Dodecagon_with_opposite_faces_identified.svg.png)
![Тетрадекагон с противоположными сторонами, обозначенными[8]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e3/14-gon_with_opposite_faces_identified.svg/150px-14-gon_with_opposite_faces_identified.svg.png)