Тетрадекагон
| Правильный тетрадекагон | |
|---|---|
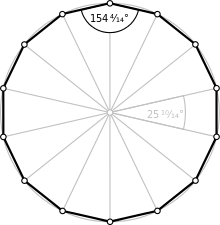 Правильный тетрадекагон | |
| Тип | Правильный многоугольник |
| Ребра и вершины | 14 |
| Символ Шлефли | {14}, т{7} |
| Диаграммы Кокстера–Дынкина |       |
| Группа симметрии | Двугранный (D 14 ), порядок 2×14 |
| Внутренний угол ( градусы ) | 154+2/7° |
| Характеристики | Выпуклый , циклический , равносторонний , изогональный , изотоксальный |
| Двойной полигон | Себя |
В геометрии тетрадекагон , тетракайдекагон или 14- угольник — это четырнадцатиугольник .
Правильный тетрадекагон
Правильный тетрадекагон имеет символ Шлефли {14} и может быть построен как квазиправильный усеченный семиугольник , t{7}, который чередует два типа ребер.
Площадь правильного тетрадекагона со стороной длиной a определяется по формуле
Строительство
Так как 14 = 2 × 7, то правильный четырнадцатиугольник не может быть построен с помощью циркуля и линейки . [1] Однако его можно построить с помощью невзиса с использованием трисектрисы угла [2] или с помощью отмеченной линейки [3] , как показано в следующих двух примерах.

анимация (1 мин 47 с) построения невзиса с радиусом описанной окружности , согласно Эндрю М. Глисону [2], основанному на трисекции угла с помощью томагавка .

анимация (1 мин 20 с) построения невуса с отмеченной линейкой, согласно Дэвиду Джонсону Лейску ( Крокетт Джонсон ). [3]
Симметрия

Правильный тетрадекагон имеет симметрию Dih 14 , порядок 28. Существует 3 подгруппы диэдральных симметрий: Dih 7 , Dih 2 и Dih 1 , а также 4 циклические группы симметрии: Z 14 , Z 7 , Z 2 и Z 1 .
Эти 8 симметрий можно увидеть в 10 различных симметриях на тетрадекагоне, большем числе, поскольку линии отражений могут проходить либо через вершины, либо через ребра. Джон Конвей обозначает их буквой и порядком группы. [4] Полная симметрия правильной формы — r28 , и ни одна симметрия не обозначена a1 . Диэдральные симметрии делятся в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров), и i , когда линии отражений проходят как через ребра, так и через вершины. Циклические симметрии в среднем столбце обозначены как g для их центрального порядка инерции.
Каждая подгруппа симметрии допускает одну или несколько степеней свободы для нерегулярных форм. Только подгруппа g14 не имеет степеней свободы, но может рассматриваться как направленные ребра .
Неправильные тетрадекагоны с самой высокой симметрией — это d14 , изогональный тетрадекагон, построенный семью зеркалами, которые могут чередовать длинные и короткие стороны, и p14 , изотоксальный тетрадекагон, построенный с равными длинами сторон, но вершинами, чередующими два различных внутренних угла. Эти две формы являются дуальными друг другу и имеют половину порядка симметрии правильного тетрадекагона.
Вскрытие
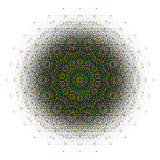 14-кубовая проекция |  84 ромбовидная диссекция |
Коксетер утверждает, что каждый зоногон (2 m -угольник, противоположные стороны которого параллельны и имеют одинаковую длину) можно разрезать на m ( m -1)/2 параллелограммов. [5] В частности, это верно для правильных многоугольников с равным числом сторон, в этом случае все параллелограммы являются ромбами. Для правильного тетрадекагона m = 7 , и его можно разделить на 21:3 набора по 7 ромбов. Это разложение основано на проекции многоугольника Петри 7-куба с 21 из 672 граней. Список OEIS : A006245 определяет число решений как 24698, включая до 14-кратных вращений и хиральных форм в отражении.
 |  | 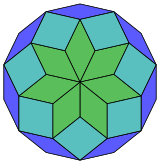 | 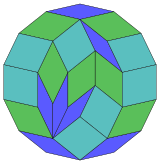 |  | 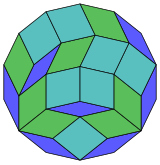 |
Нумизматическое использование
Правильный четырнадцатиугольник используется в качестве формы некоторых памятных золотых и серебряных малазийских монет, число сторон которых представляет 14 штатов Малазийской Федерации. [6]
Связанные цифры

Тетрадекаграмма — это 14-сторонний звездчатый многоугольник, представленный символом {14/n}. Существует два правильных звездчатых многоугольника : {14/3} и {14/5}, использующие одни и те же вершины, но соединяющие каждую третью или пятую точку. Существует также три соединения: {14/2} сокращается до 2{7} как два семиугольника , в то время как {14/4} и {14/6} сокращаются до 2{7/2} и 2{7/3} как два различных семиугольника , и, наконец, {14/7} сокращается до семи двуугольников .
Знаменательное применение четырнадцатиконечной звезды — флаг Малайзии , в правом верхнем углу которого изображена желтая тетрадекаграмма {14/6}, символизирующая единство тринадцати штатов с федеральным правительством .
Более глубокие усечения правильного семиугольника и гептаграмм могут производить изогональные ( вершинно-транзитивные ) промежуточные формы тетрадекаграмм с равноотстоящими вершинами и двумя длинами ребер. Другие усечения могут образовывать двойные покрывающие многоугольники 2{p/q}, а именно: t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2} и t{7/2}={14/2}=2{7}. [7]
Изотоксальные формы
Изотоксальный многоугольник можно обозначить как {p α } с внешним самым внутренним углом α, а звездчатый многоугольник {( p / q ) α }, где q — число витков , а gcd( p , q ) = 1, q < p . Изотоксальные тетрадекагоны имеют p = 7, и поскольку 7 — простое число, все решения, q = 1..6, являются многоугольниками.
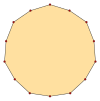 {7 α } | 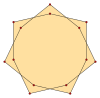 {(7/2) α } |  {(7/3) α } | 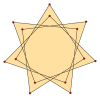 {(7/4) α } |  {(7/5) α } | 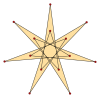 {(7/6) α } |
Петри полигоны
Правильные косые тетрадекагоны существуют как многоугольники Петри для многих многогранников более высокой размерности, показанных в этих косых ортогональных проекциях , включая:
| Петри полигоны | ||||
|---|---|---|---|---|
| Б 7 | 2И 2 (7) (4Д) | |||
 7-ортоплекс |  7-кубовый | 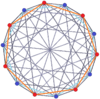 7-7 дуопирамида |  7-7 дуопризма | |
| А 13 | Д 8 | Е 8 | ||
 13-симплекс |  5 11 |  1 51 |  4 21 |  2 41 |
Ссылки
- ^ Ванцель, Пьер (1837). «Recherches sur les moyens de Reconnaître si un Problème de geométrie peau se resoudre avec la règle et le compas» (PDF) . Журнал Mathématiques : 366–372.
- ^ ab Gleason, Andrew Mattei (март 1988). "Angle trisection, the heptagon, p. 186 (Fig.1) –187" (PDF) . The American Mathematical Monthly . 95 (3): 185–194. doi :10.2307/2323624. Архивировано из оригинала (PDF) 2016-02-02.
- ^ ab Weisstein, Eric W. «Heptagon». Из MathWorld, веб-ресурса Wolfram.
- ^ Джон Х. Конвей, Хайди Бергиль, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)
- ^ Коксетер , Математические развлечения и эссе, тринадцатое издание, стр. 141
- ↑ The Numismatist , том 96, выпуски 7-12, страница 1409, Американская нумизматическая ассоциация, 1983.
- ^ Более светлая сторона математики: Труды конференции памяти Эжена Стренса по занимательной математике и ее истории, (1994), Метаморфозы многоугольников , Бранко Грюнбаум
Внешние ссылки
- Вайсштейн, Эрик В. «Тетрадекагон». MathWorld .