Теория переходного состояния

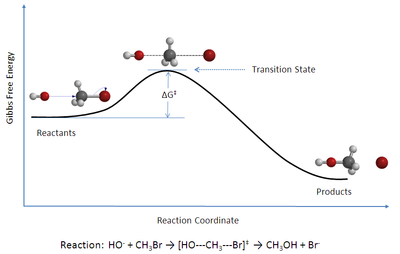
В химии теория переходного состояния ( TST ) объясняет скорости элементарных химических реакций . Теория предполагает особый тип химического равновесия (квазиравновесие) между реагентами и активированными комплексами переходного состояния . ^[1]

TST используется в первую очередь для качественного понимания того, как происходят химические реакции. TST был менее успешным в своей первоначальной цели расчета абсолютных констант скорости реакции, поскольку расчет абсолютных скоростей реакции требует точного знания поверхностей потенциальной энергии ^[2] , но он был успешным в расчете стандартной энтальпии активации (Δ H ^‡ , также пишется как Δ ^‡ H ^ɵ ), стандартной энтропии активации (Δ S ^‡ или Δ ^‡ S ^ɵ ) и стандартной энергии Гиббса активации (Δ G ^‡ или Δ ^‡ G ^ɵ ) для конкретной реакции, если ее константа скорости была экспериментально определена ( обозначение ^{‡ относится к} интересующему значению в переходном состоянии ; Δ H ^‡ — это разница между энтальпией переходного состояния и энтальпией реагентов).

Эта теория была разработана одновременно в 1935 году Генри Айрингом , тогда работавшим в Принстонском университете , и Мередит Гвинн Эванс и Майклом Полани из Манчестерского университета . ^{[3] [4] [5]} TST также называют «теорией активированного комплекса», «теорией абсолютной скорости» и «теорией абсолютных скоростей реакции». ^[6]

До разработки TST закон скорости Аррениуса широко использовался для определения энергий барьера реакции. Уравнение Аррениуса выводится из эмпирических наблюдений и игнорирует любые механистические соображения, такие как то, участвуют ли один или несколько реактивных промежуточных продуктов в превращении реагента в продукт. ^[7] Поэтому для понимания двух параметров, связанных с этим законом, предэкспоненциального множителя ( A ) и энергии активации ( Ea ), потребовалась дальнейшая разработка. TST, который привел к уравнению Эйринга , успешно решает эти две проблемы; однако между публикацией закона скорости Аррениуса в 1889 году и уравнением Эйринга, полученным из TST, в 1935 году прошло 46 лет _. В течение этого периода многие ученые и исследователи внесли значительный вклад в развитие теории.

Основные идеи теории переходного состояния следующие:

1. Скорости реакции можно изучать, исследуя активированные комплексы вблизи седловой точки поверхности потенциальной энергии . Детали того, как образуются эти комплексы, не важны. Сама седловая точка называется переходным состоянием.
2. Активированные комплексы находятся в особом равновесии (квазиравновесии) с молекулами реагентов.
3. Активированные комплексы могут превращаться в продукты, и для расчета скорости этого превращения можно использовать кинетическую теорию.

При разработке TST были использованы три подхода, которые кратко изложены ниже.

В 1884 году Якобус ван 'т Гофф предложил уравнение Вант Гоффа, описывающее температурную зависимость константы равновесия для обратимой реакции:

${\displaystyle {\ce {{A}<=> {B}}}}$

${\displaystyle {\frac {d\ln K}{dT}}={\frac {\Delta U}{RT^{2}}}}$

где Δ U — изменение внутренней энергии, K — константа равновесия реакции, R — универсальная газовая постоянная , а T — термодинамическая температура . На основе экспериментальных работ в 1889 году Сванте Аррениус предложил аналогичное выражение для константы скорости реакции, заданное следующим образом:

${\displaystyle {\frac {d\ln k}{dT}}={\frac {\Delta E}{RT^{2}}}}$

Интеграция этого выражения приводит к уравнению Аррениуса

${\displaystyle k=Ae^{-E_{a}/RT}}$

где k — константа скорости. A назывался частотным фактором (теперь называемым предэкспоненциальным коэффициентом), а E _a считался энергией активации. К началу 20 века многие приняли уравнение Аррениуса, но физическая интерпретация A и E _a оставалась неопределенной. Это привело к тому, что многие исследователи в области химической кинетики предложили различные теории того, как происходят химические реакции, в попытке связать A и E _a с молекулярной динамикой, непосредственно ответственной за химические реакции. ^{[ необходима цитата ]}

В 1910 году французский химик Рене Марселен ввел понятие стандартной энергии активации Гиббса. Его соотношение можно записать как

${\displaystyle k\propto \exp \left({\frac {-\Delta ^{\ddagger }G^{\ominus }}{RT}}\right)}$

Примерно в то же время, когда Марцелин работал над своей формулой, голландские химики Филипп Абрахам Конштамм, Франс Эппо Корнелис Шеффер и Видольд Франс Брандсма ввели стандартную энтропию активации и стандартную энтальпию активации. Они предложили следующее уравнение константы скорости

${\displaystyle k\propto \exp \left({\frac {\Delta ^{\ddagger }S^{\ominus }}{R}}\right)\exp \left({\frac {-\Delta ^{\ddagger }H^{\ominus }}{RT}}\right)}$

Однако природа этой константы до сих пор оставалась неясной.

В начале 1900 года Макс Траутц и Уильям Льюис изучали скорость реакции, используя теорию столкновений , основанную на кинетической теории газов . Теория столкновений рассматривает реагирующие молекулы как твёрдые сферы, сталкивающиеся друг с другом; эта теория пренебрегает изменениями энтропии, поскольку предполагает, что столкновения между молекулами полностью упругие.

Льюис применил свое рассмотрение к следующей реакции и получил хорошее согласие с экспериментальным результатом.

2 HI → _H2 + _I2

Однако позднее, когда тот же подход был применен к другим реакциям, обнаружились большие расхождения между теоретическими и экспериментальными результатами.

Статистическая механика сыграла значительную роль в развитии TST. Однако применение статистической механики к TST развивалось очень медленно, учитывая тот факт, что в середине 19 века Джеймс Клерк Максвелл , Людвиг Больцман и Леопольд Пфаундлер опубликовали несколько статей, в которых обсуждались равновесие и скорости реакций с точки зрения молекулярных движений и статистического распределения молекулярных скоростей.

Лишь в 1912 году французский химик А. Берту использовал закон распределения Максвелла–Больцмана, чтобы получить выражение для константы скорости.

${\displaystyle {\frac {d\ln k}{dT}}={\frac {a-bT}{RT^{2}}}}$

где a и b — константы, связанные с энергетическими терминами.

Два года спустя Рене Марселен внес существенный вклад, рассматривая ход химической реакции как движение точки в фазовом пространстве . Затем он применил статистико-механические процедуры Гиббса и получил выражение, подобное тому, которое он получил ранее из термодинамических соображений.

В 1915 году еще один важный вклад внес британский физик Джеймс Райс. На основе своего статистического анализа он пришел к выводу, что константа скорости пропорциональна «критическому приращению». Его идеи были далее развиты Ричардом Чейсом Толменом . В 1919 году австрийский физик Карл Фердинанд Герцфельд применил статистическую механику к константе равновесия и кинетическую теорию к константе скорости обратной реакции, k ₋₁ , для обратимой диссоциации двухатомной молекулы. ^[8]

${\displaystyle {\ce {AB <=>[k_1][k_{-1}] {A}+ {B}}}}$

Он получил следующее уравнение для константы скорости прямой реакции ^[9]

${\displaystyle k_{1}={\frac {k_{\mathrm {B} }T}{h}}\left(1-e^{-{\frac {h\nu }{k_{\text{B}}T}}}\right)\exp \left({\frac {-E^{\ominus }}{RT}}\right)}$

где — энергия диссоциации при абсолютном нуле, k _B — постоянная Больцмана , h — постоянная Планка , T — термодинамическая температура, — частота колебаний связи. Это выражение очень важно, поскольку впервые в уравнении скорости появился фактор k _B T / h , который является критическим компонентом TST.${\displaystyle \textstyle E^{\ominus }}$${\displaystyle \nu}$

В 1920 году американский химик Ричард Чейс Толмен развил идею Райса о критическом приращении. Он пришел к выводу, что критическое приращение (сейчас называемое энергией активации) реакции равно средней энергии всех молекул, участвующих в реакции, за вычетом средней энергии всех молекул-реагентов.

Концепция потенциальной поверхности энергии сыграла важную роль в развитии TST. Основу этой концепции заложил Рене Марселин в 1913 году. Он предположил, что ход химической реакции можно описать как точку на потенциальной поверхности энергии с координатами в атомных импульсах и расстояниях.

В 1931 году Генри Эйринг и Майкл Полани построили поверхность потенциальной энергии для реакции, представленной ниже. Эта поверхность представляет собой трехмерную диаграмму, основанную на квантово-механических принципах, а также экспериментальных данных о частотах колебаний и энергиях диссоциации.

Н + Н2 _→ Н2 ₊ Н

Через год после построения Эйринга и Полани Ганс Пельцер и Юджин Вигнер внесли важный вклад, проследив за ходом реакции на поверхности потенциальной энергии. Важность этой работы состояла в том, что в ней впервые обсуждалась концепция col или седловой точки на поверхности потенциальной энергии. Они пришли к выводу, что скорость реакции определяется движением системы через этот col.

Моделируя реакции как движение Ланжевена вдоль одномерной координаты реакции, Хендрик Крамерс смог вывести связь между формой поверхности потенциальной энергии вдоль координаты реакции и скоростями перехода системы. Формулировка основана на аппроксимации ландшафта потенциальной энергии как серии гармонических ям. В системе с двумя состояниями будет три ямы: яма для состояния A, перевернутая яма, представляющая потенциальный энергетический барьер, и яма для состояния B.

В сверхдемпфированном (или «диффузионном») режиме скорость перехода из состояния A в B связана с резонансной частотой ям через

${\displaystyle k^{A\rightarrow B}={\frac {\omega _{a}\omega _{H}}{2\pi \gamma }}\exp \left(-{\frac {E_{H}-E_{A}}{k_{\text{B}}T}}\right)}$

где — частота ямы для состояния A, — частота барьерной ямы, — вязкое затухание, — энергия верхней части барьера, — энергия нижней части ямы для состояния A, — температура системы, умноженная на постоянную Больцмана. ^[10]${\displaystyle \omega _{a}}$${\displaystyle \omega _{H}}$${\displaystyle \gamma }$${\displaystyle E_{H}}$${\displaystyle E_{A}}$${\displaystyle k_{\text{B}}T}$

Для общего затухания (избыточного или недостаточного) существует аналогичная формула. ^[11]

Одной из наиболее важных особенностей, введенных Эйрингом , Полани и Эвансом, было представление о том, что активированные комплексы находятся в квазиравновесии с реагентами. Скорость тогда прямо пропорциональна концентрации этих комплексов, умноженной на частоту ( k _B T / h ), с которой они превращаются в продукты. Ниже приводится нестрогий аргумент правдоподобия для функциональной формы уравнения Эйринга. Однако ключевой статистический механический фактор k _B T / h не будет обоснован, и представленный ниже аргумент не представляет собой истинного «вывода» уравнения Эйринга. ^[12]

Квазиравновесие отличается от классического химического равновесия, но может быть описано с использованием аналогичной термодинамической трактовки. ^{[6] [13]} Рассмотрим реакцию ниже

${\displaystyle {\ce {{A}+{B}<=>{[AB]^{\ddagger }}->{P}}}}$

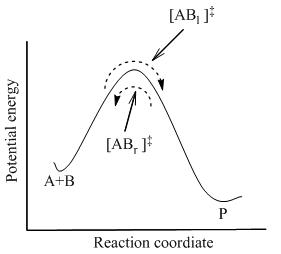
где достигается полное равновесие между всеми видами в системе, включая активированные комплексы, [AB] ^‡ . Используя статистическую механику, концентрацию [AB] ^‡ можно рассчитать через концентрацию A и B.

TST предполагает, что даже когда реагенты и продукты не находятся в равновесии друг с другом, активированные комплексы находятся в квазиравновесии с реагентами. Как показано на рисунке 2, в любой момент времени существует несколько активированных комплексов, и некоторые из них были молекулами реагентов в непосредственном прошлом, которые обозначены [AB _l ] ^‡ (так как они движутся слева направо). Остальные из них были молекулами продуктов в непосредственном прошлом ([AB _r ] ^‡ ).

В TST предполагается, что поток активированных комплексов в двух направлениях независим друг от друга. То есть, если все молекулы продукта были внезапно удалены из реакционной системы, поток [AB _r ] ^‡ останавливается, но поток слева направо все еще существует. Следовательно, если быть технически корректным, реагенты находятся в равновесии только с [AB _l ] ^‡ , активированными комплексами, которые были реагентами в непосредственном прошлом.

Активированные комплексы не следуют распределению Больцмана по энергиям, но "константу равновесия" все еще можно вывести из распределения, которому они следуют. Константу равновесия K ^‡ для квазиравновесия можно записать как

${\displaystyle K^{\ddagger }={\frac {\ce {[AB]^{\ddagger }}}{\ce {[A][B]}}}}$.

Итак, химическая активность переходного состояния AB ^‡ равна

${\displaystyle [{\ce {AB}}]^{\ddagger }=K^{\ddagger }[{\ce {A}}][{\ce {B}}]}$.

Таким образом, уравнение скорости производства продукта имеет вид

${\displaystyle {\frac {d[{\ce {P}}]}{dt}}=k^{\ddagger }[{\ce {AB}}]^{\ddagger }=k^{\ddagger }K^{\ddagger }[{\ce {A}}][{\ce {B}}]=k[{\ce {A}}][{\ce {B}}]}$,

где константа скорости k определяется выражением

${\displaystyle k=k^{\ddagger }K^{\ddagger }}$.

Здесь k ^‡ прямо пропорционален частоте колебательного режима, ответственного за преобразование активированного комплекса в продукт; частота этого колебательного режима равна . Каждая вибрация не обязательно приводит к образованию продукта, поэтому для учета этого эффекта вводится константа пропорциональности , называемая коэффициентом передачи. Таким образом , k ^‡ можно переписать как${\displaystyle \nu }$${\displaystyle \kappa }$

${\displaystyle k^{\ddagger }=\kappa \nu }$.

Для константы равновесия K ^‡ статистическая механика приводит к зависящему от температуры выражению, которое задается как

${\displaystyle K^{\ddagger }={\frac {k_{\text{B}}T}{h\nu }}K^{\ddagger '}}$( ).${\displaystyle K^{\ddagger '}=:e^{\frac {-\Delta G^{\ddagger }}{RT}}}$

Объединив новые выражения для k ^‡ и K ^‡ , можно записать новое выражение константы скорости, которое задается как

${\displaystyle k=k^{\ddagger }K^{\ddagger }=\kappa {\frac {k_{\text{B}}T}{h}}e^{\frac {-\Delta G^{\ddagger }}{RT}}=\kappa {\frac {k_{\text{B}}T}{h}}K^{\ddagger '}}$.

Поскольку по определению Δ G ^‡ = Δ H ^‡ – T Δ S ^‡ , выражение константы скорости можно разложить, чтобы получить альтернативную форму уравнения Эйринга:

${\displaystyle k=\kappa {\frac {k_{\text{B}}T}{h}}e^{\frac {\Delta S^{\ddagger }}{R}}e^{\frac {-\Delta H^{\ddagger }}{RT}}}$.

Для правильной размерности уравнение должно иметь дополнительный множитель ( c ^⊖ ) ^{1– m} для реакций, которые не являются мономолекулярными:

${\displaystyle k=\kappa {\frac {k_{\text{B}}T}{h}}e^{\frac {\Delta S^{\ddagger }}{R}}e^{\frac {-\Delta H^{\ddagger }}{RT}}(c^{\ominus })^{1-m}}$,

где c ^⊖ — стандартная концентрация 1 моль⋅л ⁻¹ , а m — молекулярность. ^[14]

Выражение константы скорости из теории переходного состояния можно использовать для расчета Δ G ^‡ , Δ H ^‡ , Δ S ^‡ и даже Δ V ^‡ (объем активации) с использованием экспериментальных данных о скорости. Эти так называемые параметры активации дают представление о природе переходного состояния , включая содержание энергии и степень порядка, по сравнению с исходными материалами и стали стандартным инструментом для выяснения механизмов реакции в физической органической химии . Свободная энергия активации, Δ G ^‡ , определяется в теории переходного состояния как энергия, такая, что выполняется. Затем параметры Δ H ^‡ и Δ S ^‡ можно вывести, определив Δ G ^‡ = Δ H ^‡ – T Δ S ^‡ при различных температурах. ${\displaystyle \Delta G^{\ddagger }=-RT\ln K^{\ddagger '}}$

Поскольку функциональная форма уравнений Эйринга и Аррениуса похожа, возникает соблазн связать параметры активации с энергией активации и предэкспоненциальными множителями обработки Аррениуса. Однако уравнение Аррениуса было выведено из экспериментальных данных и моделирует макроскопическую скорость с использованием только двух параметров, независимо от числа переходных состояний в механизме. Напротив, параметры активации могут быть найдены для каждого переходного состояния многоступенчатого механизма, по крайней мере в принципе. Таким образом, хотя энтальпия активации, Δ H ^‡ , часто приравнивается к энергии активации Аррениуса E _a , они не эквивалентны. Для стадии реакции в конденсированной фазе (например, фазе раствора) или мономолекулярной газофазной фазе E _a = Δ H ^‡ + RT . Для других газофазных реакций E _a = Δ H ^‡ + (1 − Δ n ^‡ ) RT , где Δ n ^‡ — изменение числа молекул при образовании переходного состояния. ^[15] (Таким образом, для бимолекулярного газофазного процесса E _a = Δ H ^‡ + 2 RT )

Энтропия активации, Δ S ^‡ , показывает, в какой степени переходное состояние (включая любые молекулы растворителя, вовлеченные в реакцию или возмущенные ею) более неупорядочено по сравнению с исходными материалами. Она предлагает конкретную интерпретацию предэкспоненциального фактора A в уравнении Аррениуса; для мономолекулярного одностадийного процесса выполняется грубая эквивалентность A = ( k _B T / h ) exp(1 + Δ S ^‡ / R ) (или A = ( k _B T / h ) exp(2 + Δ S ^‡ / R ) для бимолекулярных газофазных реакций). Для мономолекулярного процесса отрицательное значение указывает на более упорядоченное, жесткое переходное состояние, чем основное состояние, тогда как положительное значение отражает переходное состояние с более слабыми связями и/или большей конформационной свободой. Важно отметить, что по причинам размерности, реакции, которые являются бимолекулярными или более высокими, имеют значения Δ S ^{‡ , которые зависят от выбранного} стандартного состояния (в частности, стандартной концентрации). Для большинства последних публикаций выбрано 1 моль л ⁻¹ или 1 моль. Поскольку этот выбор является человеческой конструкцией, основанной на наших определениях единиц для молярного количества и объема, величина и знак Δ S ^‡ для одной реакции сами по себе бессмысленны; действительны только сравнения значения со значением референтной реакции «известного» (или предполагаемого) механизма, выполненные в том же стандартном состоянии. ^[16]

Объем активации находится путем взятия частной производной Δ G ^‡ по давлению (при постоянной температуре): . Это дает информацию о размере и, следовательно, степени связывания в переходном состоянии. Ассоциативный механизм, скорее всего, будет иметь отрицательный объем активации, в то время как диссоциативный механизм, скорее всего, будет иметь положительное значение. ${\displaystyle \Delta V^{\ddagger }:=(\partial \Delta G^{\ddagger }/\partial P)_{T}}$

Учитывая взаимосвязь между константой равновесия и константами скорости прямого и обратного переноса, уравнение Эйринга подразумевает, что ${\displaystyle K=k_{1}/k_{-1}}$

${\displaystyle \Delta G^{\circ }=\Delta G_{1}^{\ddagger }-\Delta G_{-1}^{\ddagger }}$.

Другим следствием TST является принцип Кертина-Хаммета : соотношение продуктов кинетически контролируемой реакции от R до двух продуктов A и B будет отражать разницу в энергиях соответствующих переходных состояний, приводящих к продукту, предполагая, что для каждого из них существует одно переходное состояние:

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=e^{-\Delta \Delta G^{\ddagger }/RT}}$( ).${\displaystyle \Delta \Delta G^{\ddagger }=\Delta G_{\mathrm {A} }^{\ddagger }-\Delta G_{\mathrm {B} }^{\ddagger }+\Delta G^{\circ }}$

(В выражении для ΔΔ G ^‡ выше есть дополнительный член, если A и B образуются из двух различных видов S _A и S _B в равновесии.) ${\displaystyle \Delta G^{\circ }=G_{\mathrm {S} _{\mathrm {A} }}^{\circ }-G_{\mathrm {S} _{\mathrm {B} }}^{\circ }}$

Для термодинамически контролируемой реакции каждая разница в RT ln 10 ≈ (1,987 × 10−3 ^ккал /моль K)(298 K)(2,303) ≈ 1,36 ккал/моль в свободных энергиях продуктов A и B приводит к 10-кратному увеличению селективности при комнатной температуре (298 K), принцип, известный как «правило 1,36»:

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=10^{-\Delta G^{\circ }/(1.36\ \mathrm {kcal/mol} )}}$( ).${\displaystyle \Delta G^{\circ }=G_{\mathrm {A} }^{\circ }-G_{\mathrm {B} }^{\circ }}$

Аналогично, каждые 1,36 ккал/моль разницы в свободной энергии активации приводят к 10-кратному увеличению селективности для кинетически контролируемого процесса при комнатной температуре: ^[17]

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=10^{-\Delta \Delta G^{\ddagger }/(1.36\ \mathrm {kcal/mol} )}}$( ).${\displaystyle \Delta \Delta G^{\ddagger }=\Delta G_{\mathrm {A} }^{\ddagger }-\Delta G_{\mathrm {B} }^{\ddagger }}$

Используя уравнение Эйринга, можно получить прямую связь между Δ G ^‡ , константами скорости первого порядка и периодом полураспада реакции при заданной температуре. При 298 К реакция с Δ G ^‡ = 23 ккал/моль имеет константу скорости k ≈ 8,4 × ¹⁰⁻⁵ с ⁻¹ и период полураспада t _1/2 ≈ 2,3 часа, цифры, которые часто округляют до k ~ 10−4 ^{с −1} и t _1/2 ~ 2 часа. Таким образом, свободная энергия активации такой величины соответствует типичной реакции, которая завершается в течение ночи при комнатной температуре. Для сравнения, переворот кресла циклогексана имеет Δ G ^‡ около 11 ккал/моль с k ~ 10 ⁵ с ⁻¹ , что делает его динамическим процессом, который происходит быстро (быстрее, чем шкала времени ЯМР) при комнатной температуре. На другом конце шкалы цис/транс- изомеризация 2-бутена имеет Δ G ^‡ около 60 ккал/моль, что соответствует k ~ 10 ⁻³¹ с ⁻¹ при 298 К. Это незначительная скорость: период полураспада на 12 порядков больше возраста Вселенной . ^[18]

В целом, TST предоставил исследователям концептуальную основу для понимания того, как происходят химические реакции. Несмотря на то, что теория широко применима, у нее есть ограничения. Например, при применении к каждому элементарному шагу многошаговой реакции теория предполагает, что каждый промежуточный продукт достаточно долгоживущий, чтобы достичь распределения энергий Больцмана перед переходом к следующему шагу. Когда промежуточные продукты очень короткоживущие, TST терпит неудачу. ^[19] В таких случаях импульс траектории реакции от реагентов к промежуточному продукту может переноситься вперед, влияя на селективность продукта. Примером такой реакции является замыкание кольца бирадикалов циклопентана, образующихся при термическом разложении в газовой фазе 2,3-диазабицикло[2.2.1]гепт-2-ена. ^{[20] [21]}

Теория переходного состояния также основана на предположении, что атомные ядра ведут себя в соответствии с классической механикой . ^[22] Предполагается, что если атомы или молекулы не сталкиваются с достаточной энергией для образования переходной структуры, то реакция не происходит. Однако, согласно квантовой механике, для любого барьера с конечным количеством энергии существует вероятность того, что частицы все еще могут туннелировать через барьер. В отношении химических реакций это означает, что есть вероятность того, что молекулы будут реагировать, даже если они не сталкиваются с достаточной энергией для преодоления энергетического барьера. ^[23] Хотя этот эффект незначителен для реакций с большими энергиями активации, он становится важным явлением для реакций с относительно низкими энергетическими барьерами, поскольку вероятность туннелирования увеличивается с уменьшением высоты барьера.

Теория переходного состояния не работает для некоторых реакций при высокой температуре. Теория предполагает, что реакционная система пройдет через седловую точку с самой низкой энергией на поверхности потенциальной энергии. Хотя это описание согласуется с реакциями, происходящими при относительно низких температурах, при высоких температурах молекулы заселяют колебательные моды с более высокой энергией; их движение становится более сложным, а столкновения могут приводить к переходным состояниям, далеким от седловой точки с самой низкой энергией. Это отклонение от теории переходного состояния наблюдается даже в простой обменной реакции между двухатомным водородом и радикалом водорода. ^[24]

Учитывая эти ограничения, было предложено несколько альтернатив теории переходного состояния. Ниже приводится краткое обсуждение этих теорий.

Любая форма теории переходного состояния, например, микроканоническая вариационная теория переходного состояния, каноническая вариационная теория переходного состояния и улучшенная каноническая вариационная теория переходного состояния, в которой переходное состояние не обязательно находится в седловой точке, называется обобщенной теорией переходного состояния.

Фундаментальным недостатком теории переходного состояния является то, что она считает любое пересечение переходного состояния реакцией от реагентов к продуктам или наоборот. В действительности молекула может пересечь эту «разделительную поверхность» и повернуться, или пересечь несколько раз и действительно прореагировать только один раз. Таким образом, не скорректированное TST, как говорят, обеспечивает верхнюю границу для коэффициентов скорости. Чтобы исправить это, вариационная теория переходного состояния изменяет местоположение разделительной поверхности, которая определяет успешную реакцию, чтобы минимизировать скорость для каждой фиксированной энергии. ^[25] Выражения скорости, полученные в этой микроканонической обработке, можно интегрировать по энергии, принимая во внимание статистическое распределение по энергетическим состояниям, чтобы получить канонические или тепловые скорости.

Развитие теории переходного состояния, в которой положение разделяющей поверхности изменяется таким образом, чтобы минимизировать константу скорости при заданной температуре.

Модификация канонической вариационной теории переходного состояния, в которой для энергий ниже пороговой энергии положение разделяющей поверхности принимается равным положению микроканонической пороговой энергии. Это заставляет вклады в константы скорости быть равными нулю, если они ниже пороговой энергии. Затем выбирается компромиссная разделяющая поверхность, чтобы минимизировать вклады в константу скорости, вносимые реагентами с более высокими энергиями.

Расширение TST на реакции, в которых одновременно задействованы два спиновых состояния, называется теорией неадиабатического переходного состояния (NA-TST).

Используя теорию колебательных возмущений, такие эффекты, как туннелирование и вариационные эффекты, можно учесть в рамках формализма SCTST .

Ферменты катализируют химические реакции со скоростями, которые поразительны по сравнению с некатализированной химией при тех же условиях реакции. Каждое каталитическое событие требует минимум трех или часто более шагов, все из которых происходят в течение нескольких миллисекунд, которые характеризуют типичные ферментативные реакции. Согласно теории переходного состояния, наименьшая часть каталитического цикла тратится на самый важный шаг, шаг переходного состояния. Первоначальные предложения теории абсолютной скорости реакции для химических реакций определяли переходное состояние как отдельный вид в координате реакции, которая определяла абсолютную скорость реакции. Вскоре после этого Лайнус Полинг предположил, что мощное каталитическое действие ферментов можно объяснить специфическим прочным связыванием с видом переходного состояния ^[26]. Поскольку скорость реакции пропорциональна доле реагента в комплексе переходного состояния, было предложено, что фермент увеличивает концентрацию реактивных видов.

Это предложение было формализовано Вольфенденом и его коллегами из Университета Северной Каролины в Чапел-Хилл , которые выдвинули гипотезу, что увеличение скорости, вызванное ферментами, пропорционально сродству фермента к структуре переходного состояния относительно комплекса Михаэлиса. ^[27] Поскольку ферменты обычно увеличивают некатализируемую скорость реакции в 10 ⁶ -10 ^{26 раз} , а комплексы Михаэлиса ^{[ необходимо разъяснение ]} часто имеют константы диссоциации в диапазоне 10 ⁻³ -10 ⁻⁶ М, предполагается, что комплексы переходного состояния связаны с константами диссоциации в диапазоне 10 ⁻¹⁴ -10 ⁻²³ М. По мере того, как субстрат переходит от комплекса Михаэлиса к продукту, химия происходит за счет вызванных ферментом изменений в распределении электронов в субстрате. Ферменты изменяют электронную структуру путем протонирования, отщепления протона, переноса электрона, геометрического искажения, гидрофобного разделения и взаимодействия с кислотами и основаниями Льюиса. Аналоги, которые напоминают структуры переходного состояния, должны, таким образом, обеспечивать самые мощные известные нековалентные ингибиторы.

Все химические превращения проходят через нестабильную структуру, называемую переходным состоянием, которая находится между химическими структурами субстратов и продуктов. Предполагается, что переходные состояния для химических реакций имеют продолжительность жизни около 10 ⁻¹³ секунд, что соответствует времени колебания одинарной связи. Не существует физического или спектроскопического метода для непосредственного наблюдения структуры переходного состояния для ферментативных реакций, однако структура переходного состояния имеет решающее значение для понимания ферментативного катализа, поскольку ферменты работают, снижая энергию активации химического превращения.

В настоящее время принято считать, что ферменты функционируют для стабилизации переходных состояний, лежащих между реагентами и продуктами, и что, следовательно, они должны прочно связывать любой ингибитор, который очень похож на такое переходное состояние. Субстраты и продукты часто участвуют в нескольких реакциях, катализируемых ферментами, тогда как переходное состояние, как правило, характерно для одного конкретного фермента, так что такой ингибитор, как правило, специфичен для этого конкретного фермента. Выявление многочисленных ингибиторов переходного состояния подтверждает гипотезу стабилизации переходного состояния для ферментативного катализа.

В настоящее время известно большое количество ферментов, взаимодействующих с аналогами переходного состояния, большинство из которых были разработаны с целью ингибирования целевого фермента. Примерами являются протеаза ВИЧ-1, рацемазы, β-лактамазы, металлопротеиназы, циклооксигеназы и многие другие.

Десорбция, а также реакции на поверхности легко описываются с помощью теории переходного состояния. Анализ адсорбции на поверхности из жидкой фазы может представлять собой проблему из-за отсутствия возможности оценить концентрацию растворенного вещества вблизи поверхности. Когда полные данные недоступны, было предложено нормализовать концентрации реагирующих видов по отношению к концентрации активных участков поверхности, приближение, называемое приближением эквивалентной плотности поверхностных реагентов (SREA). ^[28]

• Принцип Куртина–Хаммета
• Передача электронов
• теория Маркуса

• Anslyn, Eric V.; Doughtery, Dennis A., Transition State Theory and Related Topics. В Modern Physical Organic Chemistry University Science Books: 2006; стр. 365–373
• Cleland, WW, Изотопные эффекты: определение структуры переходного состояния фермента. Методы в энзимологии 1995, 249, 341–373
• Laidler, K.; King, C., Развитие теории переходного состояния. Журнал физической химии 1983, 87, (15), 2657
• Laidler, K., Теория переходного состояния на протяжении всей своей жизни. The Chemical Intelligencer 1998, 4, (3), 39
• Радзицка, А.; Вольденден, Р., Переходное состояние и мультисубстратные аналоговые ингибиторы. Методы в энзимологии 1995, 249, 284–312
• Шрамм, В. Л., Ферментативные переходные состояния и аналоговый дизайн переходного состояния. Annual Review of Biochemistry 1998, 67, 693–720
• Шрамм, В. Л., Теория ферментативного переходного состояния и аналоговый дизайн переходного состояния. Журнал биологической химии 2007, 282, (39), 28297–28300

• Простое применение TST