Кодирование по времени

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (April 2009) (Learn how and when to remove this message)

Кодирование по времени — это метод, используемый в квантовой информатике для кодирования кубита информации на фотоне . Квантовая информатика использует кубиты в качестве базового ресурса, аналогичного битам в классических вычислениях . Кубиты — это любая двухуровневая квантово-механическая система; существует множество различных физических реализаций кубитов, одной из которых является кодирование по времени.

Хотя метод кодирования time-bin очень устойчив к декогеренции , он не допускает простого взаимодействия между различными кубитами. Таким образом, он гораздо более полезен в квантовой коммуникации (такой как квантовая телепортация и квантовое распределение ключей ), чем в квантовых вычислениях .

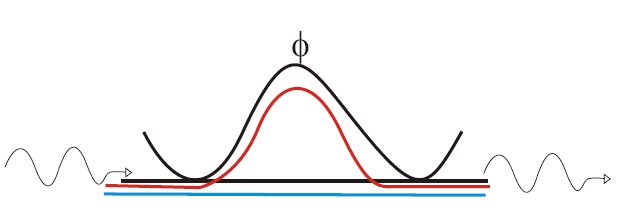
Кодирование по времени выполняется путем пропускания одного фотона через интерферометр Маха-Цендера (MZ), показанный здесь черным цветом. Фотон, идущий слева, направляется по одному из двух путей (показанных синим и красным); направление может быть сделано с помощью оптоволокна или просто в свободном пространстве с использованием зеркал и поляризационных кубов . Один из двух путей длиннее другого. Разница в длине пути должна быть больше длины когерентности фотона, чтобы убедиться, что выбранный путь можно однозначно различить. Интерферометр должен сохранять стабильную фазу, что означает, что разница в длине пути должна изменяться намного меньше, чем длина волны света во время эксперимента. Обычно для этого требуется активная стабилизация температуры.

Если фотон идет по короткому пути, говорят, что он находится в состоянии ; если он идет по длинному пути, говорят, что он находится в состоянии . Если фотон имеет ненулевую вероятность пойти по любому из путей, то он находится в когерентной суперпозиции двух состояний:${\displaystyle |0\rangle }$${\displaystyle |1\rangle }$

${\displaystyle |\psi \rangle =\alpha |0\rangle +\beta |1\rangle ,}$

Эти когерентные суперпозиции двух возможных состояний называются кубитами и являются основным компонентом квантовой информатики .

В общем, легко изменять фазу, набранную фотоном между двумя путями, например, растягивая волокно, в то время как гораздо сложнее изменять амплитуды, которые, таким образом, фиксированы, как правило, на уровне 50%. Затем созданный кубит

${\displaystyle |\psi \rangle ={\frac {|0\rangle +e^{i\phi }|1\rangle }{\sqrt {2}}},}$

который охватывает только подмножество всех возможных кубитов.

Измерение в базисе выполняется путем измерения времени прибытия фотона. Измерение в других базисах может быть достигнуто путем пропуска фотона через вторую MZ перед измерением, хотя, подобно подготовке состояния, возможные настройки измерения ограничены лишь небольшим подмножеством возможных измерений кубита.${\displaystyle \{|0\rangle ,|1\rangle \}}$

Кубиты временного интервала не страдают от деполяризации или дисперсии поляризационных мод, что делает их более подходящими для приложений волоконной оптики, чем поляризационное кодирование. Потерю фотонов легко обнаружить, поскольку отсутствие фотонов не соответствует разрешенному состоянию, что делает его более подходящим, чем кодирование на основе числа фотонов.

• Marcikic, I.; De Riedmatten, H.; Tittel, W.; Scarani, V.; Zbinden, H.; Gisin, N. (2002). "Time-bin entangled qubits for quantum communication created by femtosecond impulses". Physical Review A. 66 ( 6): 062308. arXiv : quant-ph/0205144 . Bibcode : 2002PhRvA..66f2308M. doi : 10.1103/PhysRevA.66.062308. S2CID  118932433.
• Донохью, Джон М.; Агнью, Меган; Лавуа, Джонатан; Реш, Кевин Дж. (2013). «Когерентное сверхбыстрое измерение фотонов, кодированных во временной ячейке». Physical Review Letters . 111 (15): 153602. arXiv : 1306.1250 . Bibcode :2013PhRvL.111o3602D. doi :10.1103/PhysRevLett.111.153602. PMID  24160599. S2CID  42286193.
• Мартин, А.; Кайзер, Ф.; Вернье, А.; Бевератос, А.; Скарани, В.; Танзилли, С. (2013). "Кросс-временная фотонная запутанность для квантового распределения ключей". Physical Review A . 87 (2): 020301. arXiv : 1207.6586 . Bibcode :2013PhRvA..87b0301M. doi :10.1103/PhysRevA.87.020301. S2CID  11312035.
• Marcikic, I.; De Riedmatten, H.; Tittel, W.; Zbinden, H.; Legré, M.; Gisin, N. (2004). "Распределение запутанных кубитов временного интервала на 50 км оптического волокна". Physical Review Letters . 93 (18): 180502. arXiv : quant-ph/0404124 . Bibcode :2004PhRvL..93r0502M. doi :10.1103/PhysRevLett.93.180502. PMID  15525142. S2CID  13120600.
• Питтман, Тодд (2013). «Хорошее время для кубитов с временным бункером». Физика . 6 : 110. Bibcode : 2013PhyOJ...6..110P. doi : 10.1103/Physics.6.110 . hdl : 11603/19318 .
• Гюндоган, Мустафа; Ледингем, Патрик М.; Кутлуер, Кутлу; Мацзера, Маргарита; Де Ридматтен, Хьюг (2015). «Твердотельная спин-волновая квантовая память для кубитов временного интервала». Письма о физических отзывах . 114 (23): 230501. arXiv : 1501.03980 . Бибкод : 2015PhRvL.114w0501G. doi : 10.1103/PhysRevLett.114.230501. PMID  26196784. S2CID  17555337.