Геометрия такси
Тип метрической геометрии
В геометрии такси длины красного, синего, зеленого и желтого путей равны 12 , расстоянию такси между противоположными углами, и все четыре пути являются кратчайшими путями. Вместо этого в евклидовой геометрии красный, синий и желтый пути по-прежнему имеют длину 12 , но зеленый путь является уникальным кратчайшим путем, с длиной, равной евклидову расстоянию между противоположными углами, 6√2 ≈ 8,49 .

Геометрия такси или геометрия Манхэттена — это геометрия , в которой игнорируется привычное евклидово расстояние , а расстояние между двумя точками определяется как сумма абсолютных разностей их соответствующих декартовых координат , функция расстояния (или метрика ), называемая расстоянием такси , расстоянием Манхэттена или расстоянием городского квартала . Название относится к острову Манхэттен или, в общем, к любому спланированному городу с прямоугольной сеткой улиц, в котором такси может двигаться только по направлениям сетки. В геометрии такси расстояние между любыми двумя точками равно длине их кратчайшего пути сетки. Это другое определение расстояния также приводит к другому определению длины кривой, для которой отрезок прямой между любыми двумя точками имеет ту же длину, что и путь сетки между этими точками, а не его евклидова длина.

Расстояние такси также иногда называют прямолинейным расстоянием или расстоянием L 1 (см. пространство L p ). [1] Эта геометрия использовалась в регрессионном анализе с 18 века и часто упоминается как ЛАССО . Ее геометрическая интерпретация восходит к неевклидовой геометрии 19 века и принадлежит Герману Минковскому .

В двумерном реальном координатном пространстве расстояние такси между двумя точками и равно . То есть, это сумма абсолютных значений разностей обеих координат. Р 2 {\displaystyle \mathbb {R} ^{2}} ( х 1 , у 1 ) {\displaystyle (x_{1},y_{1})} ( х 2 , у 2 ) {\displaystyle (x_{2},y_{2})} | х 1 − х 2 | + | у 1 − у 2 | {\displaystyle \left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|}

Формальное определение

Расстояние такси, , между двумя точками в n -мерном вещественном координатном пространстве с фиксированной декартовой системой координат , является суммой длин проекций отрезка прямой между точками на оси координат . Более формально, например, в , расстояние такси между и равно г Т {\displaystyle d_{\text{T}}} п = ( п 1 , п 2 , … , п н )  и  д = ( д 1 , д 2 , … , д н ) {\displaystyle \mathbf {p} =(p_{1},p_{2},\dots ,p_{n}){\text{ и }}\mathbf {q} =(q_{1},q_{2},\dots ,q_{n})} г Т ( п , д ) = ‖ п − д ‖ Т = ∑ я = 1 н | п я − д я | {\displaystyle d_{\text{T}}(\mathbf {p} ,\mathbf {q} )=\left\|\mathbf {p} -\mathbf {q} \right\|_{\text{T}}=\sum _{i=1}^{n}\left|p_{i}-q_{i}\right|} Р 2 {\displaystyle \mathbb {R} ^{2}} п = ( п 1 , п 2 ) {\displaystyle \mathbf {p} =(p_{1},p_{2})} д = ( д 1 , д 2 ) {\displaystyle \mathbf {q} =(q_{1},q_{2})} | п 1 − д 1 | + | п 2 − д 2 | . {\displaystyle \left|p_{1}-q_{1}\right|+\left|p_{2}-q_{2}\right|.}

История

Метрика L 1 использовалась в регрессионном анализе в качестве меры качества соответствия в 1757 году Роджером Джозефом Босковичем . [2] Интерпретация ее как расстояния между точками в геометрическом пространстве относится к концу 19 века и развитию неевклидовых геометрий . В частности, она появилась в 1910 году в работах Фридьеша Рисса и Германа Минковского . Формализация пространств L p , которые включают геометрию такси как частный случай, приписывается Риссу. [3] Разрабатывая геометрию чисел , Герман Минковский установил свое неравенство Минковского , заявив, что эти пространства определяют нормированные векторные пространства . [4]

Название «геометрия такси» было введено Карлом Менгером в брошюре 1952 года « Вам понравится геометрия» , сопровождавшей геометрическую выставку, предназначенную для широкой публики в Музее науки и промышленности в Чикаго. [5]

Характеристики

Рассматриваемое как дополнительная структура, наложенная на евклидово пространство , расстояние такси зависит от ориентации системы координат и изменяется при евклидовом вращении пространства, но не зависит от переноса или отражений, совмещенных с осями . Геометрия такси удовлетворяет всем аксиомам Гильберта (формализация евклидовой геометрии ), за исключением того, что конгруэнтность углов не может быть определена так, чтобы точно соответствовать евклидовой концепции, и при правдоподобных определениях конгруэнтных углов такси аксиома сторона-угол-сторона не выполняется, поскольку в общем случае треугольники с двумя конгруэнтными сторонами такси и конгруэнтным углом между ними не являются конгруэнтными треугольниками .

Сферы

Точки сетки на окружности в геометрии такси, поскольку сетка становится тоньше

В любом метрическом пространстве сфера представляет собой набор точек на фиксированном расстоянии, радиусе , от определенной центральной точки. В то время как евклидова сфера круглая и вращательно-симметричная, при расстоянии такси форма сферы представляет собой кросс-политоп , n -мерное обобщение правильного октаэдра , точки которого удовлетворяют уравнению: п {\displaystyle \mathbf {п} }

г Т ( п , с ) = ∑ я = 1 н | п я − с я | = г , {\displaystyle d_{\text{T}}(\mathbf {p} ,\mathbf {c} )=\sum _{i=1}^{n}|p_{i}-c_{i}|=r,}

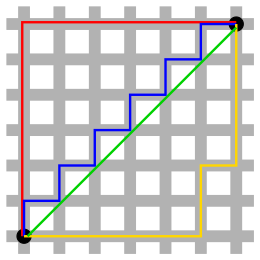
где - центр, а r - радиус. Точки на единичной сфере , сфере радиуса 1 с центром в начале координат , удовлетворяют уравнению с {\displaystyle \mathbf {c} } п {\displaystyle \mathbf {п} } г Т ( п , 0 ) = ∑ я = 1 н | п я | = 1. {\textstyle d_{\text{T}}(\mathbf {p},\mathbf {0})=\sum _{i=1}^{n}|p_{i}|=1.}

В двумерной геометрии такси сфера (называемая окружностью ) представляет собой квадрат, ориентированный по диагонали к осям координат. Изображение справа показывает красным множество всех точек на квадратной сетке с фиксированным расстоянием от синего центра. По мере того, как сетка становится тоньше, красных точек становится больше, и в пределе они стремятся к непрерывному наклонному квадрату. Каждая сторона имеет длину такси 2 r , поэтому окружность равна 8 r . Таким образом, в геометрии такси значение аналога постоянной окружности π , отношения окружности к диаметру , равно 4.

Закрытый шар (или замкнутый диск в двумерном случае) — это заполненная сфера, множество точек на расстоянии, меньшем или равном радиусу от определенного центра. Для клеточных автоматов на квадратной сетке диск такси — это фон-неймановская окрестность радиуса r его центра.

Круг радиуса r для расстояния Чебышева ( метрика L ∞ ) на плоскости также является квадратом со стороной длиной 2 r , параллельной осям координат, поэтому плоское расстояние Чебышева можно рассматривать как эквивалентное путем вращения и масштабирования плоскому расстоянию такси. Однако эта эквивалентность между метриками L 1 и L ∞ не распространяется на более высокие измерения.

Всякий раз, когда каждая пара в наборе этих окружностей имеет непустое пересечение, существует точка пересечения для всего набора; следовательно, манхэттенское расстояние образует инъективное метрическое пространство .

Длина дуги

Пусть будет непрерывно дифференцируемой функцией. Пусть будет длиной дуги такси графика на некотором интервале . Возьмем разбиение интервала на равные бесконечно малые подынтервалы, и пусть будет длиной такси поддуги . Тогда [6] у = ф ( х ) {\displaystyle y=f(x)} с {\displaystyle с} ф {\displaystyle f} [ а , б ] {\displaystyle [а,б]} Δ с я {\displaystyle \Дельта s_{i}} я й {\displaystyle i^{\text{й}}}

Δ с я = Δ х я + Δ у я = Δ х я + | ф ( х я ) − ф ( х я − 1 ) | . {\displaystyle \Delta s_{i}=\Delta x_{i}+\Delta y_{i}=\Delta x_{i}+|f(x_{i})-f(x_{i-1})|.}

По теореме о среднем значении существует некоторая точка между и такая, что . [7] Тогда предыдущее уравнение можно записать х я ∗ {\displaystyle x_{i}^{*}} х я {\displaystyle x_{i}} х я − 1 {\displaystyle x_{i-1}} ф ( х я ) − ф ( х я − 1 ) = ф ′ ( х я ∗ ) г х я {\displaystyle f(x_{i})-f(x_{i-1})=f'(x_{i}^{*})dx_{i}}

Δ с я = Δ х я + | ф ′ ( х я ∗ ) | Δ х я = Δ х я ( 1 + | ф ′ ( х я ∗ ) | ) . {\displaystyle \Delta s_{i}=\Delta x_{i}+|f'(x_{i}^{*})|\Delta x_{i}=\Delta x_{i}(1+|f'(x_{i}^{*})|).}

Тогда задается как сумма каждого разбиения по , поскольку они становятся произвольно малыми . с {\displaystyle с} с {\displaystyle с} [ а , б ] {\displaystyle [а,б]}

Кривые, определяемые монотонными возрастающими или убывающими функциями, имеют одинаковую длину дуги такси, если они имеют одни и те же конечные точки.

с = лим н → ∞ ∑ я = 1 н Δ х я ( 1 + | ф ′ ( х я ∗ ) | ) = ∫ а б 1 + | ф ′ ( х ) | г х {\displaystyle {\begin{align}s&=\lim _{n\rightarrow \infty }\sum _{i=1}^{n}\Delta x_{i}(1+|f'(x_{i}^{*})|)\\&=\int _{a}^{b}1+|f'(x)|\,dx\end{align}}}

Чтобы проверить это, возьмем круг такси с радиусом, центрированным в начале координат. Его кривая в первом квадранте задается длиной г {\displaystyle r} ф ( х ) = − х + г {\displaystyle f(x)=-x+r}

с = ∫ 0 г 1 + | − 1 | г х = 2 г {\displaystyle s=\int _{0}^{r}1+|-1|dx=2r}

Умножение этого значения на для учета оставшихся квадрантов дает , что согласуется с окружностью круга такси. [8] Теперь возьмем евклидову окружность радиуса с центром в начале координат, которая задается как . Длина ее дуги в первом квадранте задается как 4 {\displaystyle 4} 8 г {\displaystyle 8r} г {\displaystyle r} ф ( х ) = г 2 − х 2 {\displaystyle f(x)={\sqrt {r^{2}-x^{2}}}}

с = ∫ 0 г 1 + | − х г 2 − х 2 | г х = х + г 2 − х 2 | 0 г = г − ( − г ) = 2 г {\displaystyle {\begin{aligned}s&=\int _{0}^{r}1+|{\frac {-x}{\sqrt {r^{2}-x^{2}}}}|dx\\&=x+{\sqrt {r^{2}-x^{2}}}{\bigg |}_{0}^{r}\\&=r-(-r)\\&=2r\end{aligned}}}

Учет оставшихся квадрантов дает снова. Следовательно, окружность круга такси и евклидова окружность в метрике такси равны. [9] Фактически, для любой функции , которая является монотонной и дифференцируемой с непрерывной производной на интервале , длина дуги над равна . [10] 4 × 2 r = 8 r {\displaystyle 4\times 2r=8r} f {\displaystyle f} [ a , b ] {\displaystyle [a,b]} f {\displaystyle f} [ a , b ] {\displaystyle [a,b]} ( b − a ) + ∣ f ( b ) − f ( a ) ∣ {\displaystyle (b-a)+\mid f(b)-f(a)\mid }

Конгруэнтность треугольника

Два равнобедренных прямоугольных треугольника такси. Три угла и два катета равны, но треугольники не равны. Поэтому ASASA не является теоремой о конгруэнтности в геометрии такси.

Два треугольника конгруэнтны тогда и только тогда, когда три соответствующие стороны равны по расстоянию и три соответствующих угла равны по мере. Существует несколько теорем, которые гарантируют конгруэнтность треугольников в евклидовой геометрии, а именно: Угол-Угол-Сторона (AAS), Угол-Сторона-Угол (ASA), Сторона-Угол-Сторона (SAS) и Сторона-Сторона-Сторона (SSS). Однако в геометрии такси только SASAS гарантирует конгруэнтность треугольников. [11]

Возьмем, к примеру, два равнобедренных прямоугольных треугольника такси, углы которых составляют 45-90-45. Два катета обоих треугольников имеют длину такси 2, но гипотенузы не равны. Этот контрпример исключает AAS, ASA и SAS. Он также исключает AASS, AAAS и даже ASASA. Наличие трех равных углов и двух сторон не гарантирует равенства треугольников в геометрии такси. Следовательно, единственная теорема о равенстве треугольников в геометрии такси — это SASAS, где все три соответствующие стороны должны быть равны, и по крайней мере два соответствующих угла должны быть равны. [12] Этот результат в основном обусловлен тем фактом, что длина отрезка прямой зависит от его ориентации в геометрии такси.

Приложения

Сжатое зондирование

При решении недоопределенной системы линейных уравнений член регуляризации для вектора параметров выражается через норму (геометрию такси) вектора. [13] Этот подход появляется в структуре восстановления сигнала, называемой сжатым зондированием . ℓ 1 {\displaystyle \ell _{1}}

Различия в частотных распределениях

Геометрия такси может использоваться для оценки различий в дискретных распределениях частот. Например, в сплайсинге РНК позиционные распределения гексамеров , которые отображают вероятность появления каждого гексамера в каждом заданном нуклеотиде вблизи сайта сплайсинга, можно сравнить с расстоянием L1. Каждое распределение позиций может быть представлено в виде вектора, где каждая запись представляет вероятность того, что гексамер начнется с определенного нуклеотида. Большое расстояние L1 между двумя векторами указывает на существенное различие в природе распределений, тогда как малое расстояние обозначает распределения схожей формы. Это эквивалентно измерению площади между двумя кривыми распределения, поскольку площадь каждого сегмента является абсолютной разницей между правдоподобиями двух кривых в этой точке. При суммировании для всех сегментов это дает ту же меру, что и расстояние L1. [14]

Смотрите также

Сравнение расстояний Чебышева, Евклида и такси для гипотенузы треугольника 3-4-5 на шахматной доске
  • Такси метрическое со светофорами

Ссылки

  1. ^ Блэк, Пол Э. «Манхэттенское расстояние». Словарь алгоритмов и структур данных . Получено 6 октября 2019 г.
  2. ^ Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Издательство Гарвардского университета. ISBN 9780674403406. Получено 6 октября 2019 г. .
  3. ^ Рисс, Фридьес (1910). «Untersuchungen über Systeme integrierbarer Funktionen». Mathematische Annalen (на немецком языке). 69 (4): 449–497 . doi : 10.1007/BF01457637. hdl : 10338.dmlcz/128558 . S2CID  120242933.
  4. ^ Минковский, Герман (1910). Геометрия дер Зален (на немецком языке). Лейпциг и Берлин: Р. Г. Тойбнер. ЖФМ  41.0239.03. МР  0249269 . Проверено 6 октября 2019 г.
  5. ^ Менгер, Карл (1952). Вам понравится геометрия. Путеводитель по выставке геометрии Иллинойсского технологического института . Чикаго: Музей науки и промышленности.
    Голланд, Луиза (1990). «Карл Менгер и геометрия такси». Mathematics Magazine . 63 (5): 326– 327. doi :10.1080/0025570x.1990.11977548.
  6. ^ Heinbockel, JH (2012). Введение в исчисление. Том II . Old Dominion University. С.  54–55 .
  7. ^ Penot, JP (1988-01-01). "О теореме о среднем значении". Оптимизация . 19 (2): 147– 156. doi :10.1080/02331938808843330. ISSN  0233-1934.
  8. ^ Петрович, Майя; Малешевич, Бранко; Баньяк, Боян; Обрадович, Ратко (2014). Геометрия некоторых кривых такси . 4-я Международная научная конференция по геометрии и графике. Сербское общество геометрии и графики, Нишский университет, Сербия. arXiv : 1405.7579 .
  9. ^ Кемп, Обри (2018). Обобщение и перенос математических определений из евклидовой геометрии в геометрию такси (кандидатская диссертация). Университет штата Джорджия. doi : 10.57709/12521263 .
  10. ^ Томпсон, Кевин П. (2011). «Природа длины, площади и объема в геометрии такси». Международный электронный журнал геометрии . 4 (2): 193–207 . arXiv : 1101.2922 .
  11. ^ Миронычев, Александр (2018). «Условия SAS и SSA для конгруэнтных треугольников». Журнал математики и системной науки . 8 (2): 59–66 .
  12. ^ THOMPSON, KEVIN; DRAY, TEVIAN (2000). «Углы такси и тригонометрия». Pi Mu Epsilon Journal . 11 (2): 87– 96. ISSN  0031-952X. JSTOR  24340535.
  13. ^ Донохо, Дэвид Л. (23 марта 2006 г.). «Для большинства больших недоопределенных систем линейных уравнений минимальное решение -норма также является самым разреженным решением». Сообщения по чистой и прикладной математике . 59 (6): 797– 829. doi :10.1002/cpa.20132. S2CID  8510060. ℓ 1 {\displaystyle \ell _{1}}
  14. ^ Lim, Kian Huat; Ferraris, Luciana; Filloux, Madeleine E.; Raphael, Benjamin J.; Fairbrother, William G. (5 июля 2011 г.). «Использование позиционного распределения для идентификации элементов сплайсинга и прогнозирования дефектов пре-мРНК-процессинга в генах человека». Труды Национальной академии наук Соединенных Штатов Америки . 108 (27): 11093– 11098. Bibcode : 2011PNAS..10811093H . doi : 10.1073/pnas.1101135108 . PMC 3131313. PMID  21685335. 

Дальнейшее чтение

  • Вайсштейн, Эрик В. «Метрика такси». MathWorld .
  • Malkevitch, Joe (1 октября 2007 г.). «Такси!». Американское математическое общество . Получено 6 октября 2019 г.


Retrieved from "https://en.wikipedia.org/w/index.php?title=Taxicab_geometry&oldid=1264160391"