фактор Лоренца

Фактор Лоренца или член Лоренца (также известный как гамма-фактор ^[1] ) — это безразмерная величина, выражающая, насколько сильно изменяются измерения времени, длины и других физических свойств объекта при его движении. Выражение появляется в нескольких уравнениях специальной теории относительности и возникает при выводе преобразований Лоренца . Название происходит от его более раннего появления в лоренцевской электродинамике — названной в честь голландского физика Хендрика Лоренца . ^[2]

Обычно обозначается как γ (греческая строчная буква гамма ). Иногда (особенно при обсуждении сверхсветового движения ) фактор записывается как Γ (греческая заглавная -гамма), а не как γ .

Фактор Лоренца γ определяется как ^[3], где:$${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\sqrt {\frac {c^{2}}{c^{2}-v^{2}}}}={\frac {c}{\sqrt {c^{2}-v^{2}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}={\frac {dt}{d\tau }},}$$

• v — относительная скорость между инерциальными системами отсчета,
• c — скорость света в вакууме,
• β — отношение v к c ,
• t — координатное время ,
• τ — собственное время для наблюдателя (измерение интервалов времени в собственной системе отсчета наблюдателя).

Это наиболее часто используемая на практике форма, хотя и не единственная (альтернативные формы см. ниже).

Чтобы дополнить определение, некоторые авторы определяют обратную величину ^[4] см. формулу сложения скоростей .$${\displaystyle \alpha ={\frac {1}{\gamma }}={\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\ ={\sqrt {1-{\beta }^{2}}};}$$

Ниже приведен список формул из специальной теории относительности, в которых γ используется в качестве сокращения: ^{[3] [5]}

• Преобразование Лоренца : простейший случай — это усиление в направлении x (более общие формы, включая произвольные направления и вращения, здесь не перечисленные), которое описывает, как пространственно-временные координаты изменяются от одной инерциальной системы отсчета с использованием координат ( x , y , z , t ) к другой ( x ′ , y ′ , z ′ , t ′ ) с относительной скоростью v :$${\displaystyle {\begin{align}t'&=\gamma \left(t-{\tfrac {vx}{c^{2}}}\right),\\[1ex]x'&=\gamma \left(x-vt\right).\end{align}}}$$

Следствиями вышеприведенных преобразований являются результаты:

• Замедление времени : время ( ∆ t ′ ) между двумя тиками, измеренное в системе отсчета, в которой движутся часы, больше, чем время ( ∆ t ) между этими тиками, измеренное в системе отсчета, в которой часы находятся в состоянии покоя:$${\displaystyle \Дельта t'=\гамма \Дельта t.}$$
• Сокращение длины : длина ( ∆ x ′ ) объекта, измеренная в системе, в которой он движется, короче его длины ( ∆ x ) в его собственной системе покоя:$${\displaystyle \Delta x'=\Delta x/\gamma.}$$

Применение закона сохранения импульса и энергии приводит к следующим результатам:

• Релятивистская масса : масса m движущегося объекта зависит оти массы покоя m 0 _:${\displaystyle \гамма}$ $${\displaystyle m=\гамма m_{0}.}$$
• Релятивистский импульс : соотношение релятивистского импульса принимает ту же форму, что и для классического импульса, но с использованием указанной выше релятивистской массы:$${\displaystyle {\vec {p}}=m{\vec {v}}=\gamma m_{0}{\vec {v}}.}$$
• Релятивистская кинетическая энергия : Соотношение релятивистской кинетической энергии принимает слегка измененную форму:Посколькуявляется функцией, нерелятивистский предел дает, как и ожидалось из ньютоновских соображений.$${\displaystyle E_{k}=EE_{0}=(\gamma -1)m_{0}c^{2}}$$${\displaystyle \гамма}$${\displaystyle {\tfrac {v}{c}}}$${\textstyle \lim _{v/c\to 0}E_{k}={\tfrac {1}{2}}m_{0}v^{2}}$

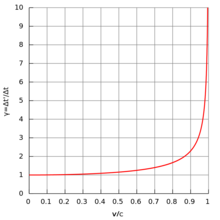
В таблице ниже левый столбец показывает скорости как различные доли скорости света (т.е. в единицах c ). Средний столбец показывает соответствующий фактор Лоренца, последний является обратной величиной. Значения, выделенные жирным шрифтом, являются точными.

Существуют и другие способы записи фактора. Выше использовалась скорость v , но связанные переменные, такие как импульс и быстрота, также могут быть удобными.

Решение предыдущего уравнения релятивистского импульса для γ приводит к Эта форма используется редко, хотя она появляется в распределении Максвелла-Юттнера . ^[6]$${\displaystyle \gamma ={\sqrt {1+\left({\frac {p}{m_{0}c}}\right)^{2}}}\,.}$$

Применение определения скорости как гиперболического угла : ^[7] также приводит к γ (используя гиперболические тождества ):${\displaystyle \varphi}$$${\displaystyle \tanh \varphi =\beta }$$$${\displaystyle \gamma =\cosh \varphi ={\frac {1}{\sqrt {1-\tanh ^{2}\varphi }}}={\frac {1}{\sqrt {1-\beta ^{2}}}}.}$$

Используя свойство преобразования Лоренца , можно показать, что быстрота аддитивна, полезное свойство, которого нет у скорости. Таким образом, параметр быстроты образует однопараметрическую группу , основу для физических моделей.

Тождество Банни представляет фактор Лоренца в терминах бесконечного ряда функций Бесселя : ^[8]$${\displaystyle \sum _{m=1}^{\infty }\left(J_{m-1}^{2}(m\beta )+J_{m+1}^{2}(m\beta )\right)={\frac {1}{\sqrt {1-\beta ^{2}}}}.}$$

Фактор Лоренца имеет ряд Маклорена : который является частным случаем биномиального ряда .$${\displaystyle {\begin{aligned}\gamma &={\dfrac {1}{\sqrt {1-\beta ^2}}}}\\[1ex]&=\sum _{n=0}^{\infty }\beta ^{2n}\prod _{k=1}^{n}\left({\dfrac {2k-1}{2k}}\right)\\[1ex]&=1+{\tfrac {1}{2}}\beta ^2}+{\tfrac {3}{8}}\beta ^4}+{\tfrac {5}{16}}\beta ^6}+{\tfrac {35}{128}}\beta ^8}+{\tfrac {63}{256}}\beta ^10}+\cdots ,\end{выровнено}}}$$

Приближение может быть использовано для расчета релятивистских эффектов на малых скоростях. Оно выполняется с погрешностью 1% для v  < 0,4  c ( v  < 120 000 км/с) и с погрешностью 0,1% для v  < 0,22  c ( v  < 66 000 км/с).${\textstyle \гамма \приблизительно 1+{\frac {1}{2}}\бета ^{2}}$

Усеченные версии этой серии также позволяют физикам доказать, что специальная теория относительности сводится к ньютоновской механике на низких скоростях. Например, в специальной теории относительности справедливы следующие два уравнения:

$${\displaystyle {\begin{aligned}\mathbf {p} &=\gamma m\mathbf {v} ,\\E&=\gamma mc^{2}.\end{aligned}}}$$

Для и , соответственно, они сводятся к своим ньютоновским эквивалентам:${\displaystyle \гамма \приблизительно 1}$${\textstyle \гамма \приблизительно 1+{\frac {1}{2}}\бета ^{2}}$

$${\displaystyle {\begin{aligned}\mathbf {p} &=m\mathbf {v} ,\\E&=mc^{2}+{\tfrac {1}{2}}mv^{2}.\end{aligned}}}$$

Уравнение фактора Лоренца также можно инвертировать, чтобы получить: Оно имеет асимптотическую форму$${\displaystyle \beta = {\sqrt {1-{\frac {1}{\gamma ^{2}}}}}.}$$$${\displaystyle \beta =1-{\tfrac {1}{2}}\gamma ^{-2}-{\tfrac {1}{8}}\gamma ^{-4}-{\tfrac {1}{16}}\gamma ^{-6}-{\tfrac {5}{128}}\gamma ^{-8}+\cdots \,.}$$

Первые два члена иногда используются для быстрого вычисления скоростей из больших значений γ . Приближение выполняется с точностью 1% для γ > 2 и с точностью 0,1% для γ > 3,5 .${\textstyle \бета \приблизительно 1-{\frac {1}{2}}\гамма ^{-2}}$

Стандартная модель длительных гамма-всплесков (GRB) утверждает, что эти взрывы являются ультрарелятивистскими (начальный γ больше примерно 100), что привлекается для объяснения так называемой проблемы «компактности»: в отсутствие этого ультрарелятивистского расширения выбросы были бы оптически толстыми для образования пар при типичных пиковых спектральных энергиях в несколько сотен кэВ, тогда как мгновенное излучение, как наблюдается, является нетепловым. ^[9]

Мюоны , субатомные частицы, движутся с такой скоростью, что имеют относительно высокий фактор Лоренца и, следовательно, испытывают экстремальное замедление времени . Поскольку среднее время жизни мюонов составляет всего 2,2  мкс , мюоны, образующиеся в результате столкновений космических лучей на высоте 10 км (6,2 мили) в атмосфере Земли, не должны обнаруживаться на земле из-за скорости их распада. Однако примерно 10% мюонов от этих столкновений все еще обнаруживаются на поверхности, тем самым демонстрируя влияние замедления времени на скорость их распада. ^[10]

• Инерциальная система отсчета
• Правильная скорость
• Псевдобыстрота

• Меррифилд, Майкл. "γ – Лоренц-фактор (и замедление времени)". Шестьдесят символов . Брэди Харан для Ноттингемского университета .
• Меррифилд, Майкл. «γ2 – Gamma Reloaded». Шестьдесят символов . Брэди Харан для Ноттингемского университета .