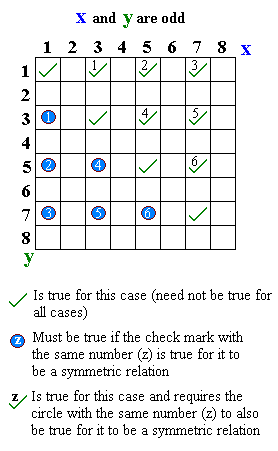
Симметричное отношение

Транзитивные  бинарные отношения в т е
Симметричный Антисимметричный Подключен Обоснованный Имеет соединения Имеет встречает Рефлексивный Нерефлексивный Асимметричный Всего, Полуконнекc Антирефлексивный ​ Отношение эквивалентности И ✗ ✗ ✗ ✗ ✗ И ✗ ✗ Предварительный заказ (квазизаказ) ✗ ✗ ✗ ✗ ✗ ✗ И ✗ ✗ Частичный заказ ✗ И ✗ ✗ ✗ ✗ И ✗ ✗ Всего предзаказов ✗ ✗ И ✗ ✗ ✗ И ✗ ✗ Общий заказ ✗ И И ✗ ✗ ✗ И ✗ ✗ Предварительный заказ ✗ ✗ И И ✗ ✗ И ✗ ✗ Хорошо-квази-упорядочение ✗ ✗ ✗ И ✗ ✗ И ✗ ✗ Хорошо упорядоченный ✗ И И И ✗ ✗ И ✗ ✗ Решетка ✗ И ✗ ✗ И И И ✗ ✗ Join-полурешетка ✗ И ✗ ✗ И ✗ И ✗ ✗ Встреча-полурешетка ✗ И ✗ ✗ ✗ И И ✗ ✗ Строгий частичный порядок ✗ И ✗ ✗ ✗ ✗ ✗ И И Строгий слабый порядок ✗ И ✗ ✗ ✗ ✗ ✗ И И Строгий общий порядок ✗ И И ✗ ✗ ✗ ✗ И И Симметричный Антисимметричный Подключен Обоснованный Имеет соединения Имеет встречает Рефлексивный Нерефлексивный Асимметричный Определения, для всех и${\displaystyle а,б}$${\displaystyle S\neq \varnothing:}$ ${\displaystyle {\begin{align}&aRb\\\Стрелка вправо {}&bRa\end{align}}}$ ${\displaystyle {\begin{align}aRb{\text{ и }}&bRa\\\Стрелка вправо a={}&b\end{align}}}$ ${\displaystyle {\begin{align}a\neq {}&b\Rightarrow \\aRb{\text{ или }}&bRa\end{align}}}$ ${\displaystyle {\begin{align}\min S\\{\text{exists}}\end{align}}}$ ${\displaystyle {\begin{align}a\vee b\\{\text{существует}}\end{align}}}$ ${\displaystyle {\begin{align}a\wedge b\\{\text{существует}}\end{align}}}$ ${\displaystyle аРа}$ ${\displaystyle {\text{не}}aRa}$ ${\displaystyle {\begin{align}aRb\Rightarrow \\{\text{not}}bRa\end{align}}}$
Иуказывает, что свойство столбца всегда верно для термина строки (слева), в то время как ✗ указывает, что свойство не гарантируется в общем случае (оно может выполняться, а может и не выполняться). Например, то, что каждое отношение эквивалентности симметрично, но не обязательно антисимметрично, обозначается в столбце «Симметрично» и ✗ в столбце «Антисимметрично» соответственно.И Все определения неявно требуют, чтобы однородное отношение было транзитивным : для всех, если и то Определение термина может требовать дополнительных свойств, которые не перечислены в этой таблице.${\displaystyle R}$${\displaystyle а,б,в,}$${\displaystyle aRb}$${\displaystyle bRc}$${\displaystyle aRc.}$

Симметричное отношение — это тип бинарного отношения . Формально бинарное отношение R над множеством X является симметричным, если: ^[1]

${\displaystyle \forall a,b\in X(aRb\Leftrightarrow bRa),}$

где обозначение aRb означает, что ( a , b ) ∈ R.

Примером может служить отношение «равно», поскольку если a = b истинно, то b = a также истинно. Если R ^T представляет собой обратное R , то R симметрично тогда и только тогда, когда R = R ^T . ^[2]

Симметрия, наряду с рефлексивностью и транзитивностью , являются тремя определяющими свойствами отношения эквивалентности . ^[1]

• «равно» ( равенство ) (тогда как «меньше» не является симметричным)
• « сравнимо с» для элементов частично упорядоченного множества
• "... и ... странные":

• «состоит в браке с» (в большинстве правовых систем)
• "является полностью биологическим братом"
• "является омофоном "
• "является коллегой"
• "является товарищем по команде"

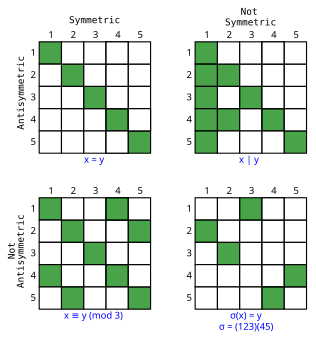
По определению непустое отношение не может быть одновременно симметричным и асимметричным (где если a связано с b , то b не может быть связано с a (таким же образом)). Однако отношение не может быть ни симметричным, ни асимметричным, что имеет место для «меньше или равно» и «охотится на»).

Симметрия и антисимметрия (где a может быть связана с b, а b может быть связана с a, только если a = b ) на самом деле независимы друг от друга, как показывают эти примеры.

• Симметричное и транзитивное отношение всегда квазирефлексивно . ^[a]
• Один из способов подсчета симметричных отношений на n элементах заключается в том, что в их двоичном матричном представлении верхний правый треугольник полностью определяет отношение, и оно может быть задано произвольно, таким образом, существует столько симметричных отношений, сколько n × n двоичных верхних треугольных матриц, 2 ^{n ( n +1)/2} . ^[3]

Обратите внимание, что S ( n , k ) относится к числам Стирлинга второго рода .

• Свойство коммутативности  – Свойство некоторых математических операций
• Симметрия в математике
• Симметрия  – Математическая инвариантность относительно преобразований