Строгий 2-й категории

В теории категорий строгая 2-категория — это категория с « морфизмами между морфизмами», то есть, где каждое hom-множество само по себе несет структуру категории. Формально ее можно определить как категорию, обогащенную над Cat ( категорией категорий и функторов , с моноидальной структурой, заданной произведением категорий ).

Понятие 2-категории впервые было введено Чарльзом Эресманном в его работе об обогащенных категориях в 1965 году. ^[1] Более общее понятие бикатегории (или слабой 2- категории ), где композиция морфизмов ассоциативна только с точностью до 2-изоморфизма, было введено в 1968 году Жаном Бенабу . ^[2]

Категория 2  C состоит из:

• Класс 0- клеток ( или объектов ) A , B , ....
• Для всех объектов A и B , категория . Объекты этой категории называются 1- ячейками , а ее морфизмы называются 2- ячейками ; композиция в этой категории обычно записывается или и называется вертикальной композицией или композицией вдоль 1- ячейки .${\displaystyle \mathbf {C} (A,B)}$${\displaystyle f,g:A\to B}$${\displaystyle \alpha :f\Стрелка вправо g}$${\displaystyle \circ}$${\displaystyle \circ _{1}}$
• Для любого объекта  A существует функтор из терминальной категории (с одним объектом и одной стрелкой) в , который выбирает тождественную 1-клеточную  id _A на A и ее тождественную 2-клеточную  id _{id A} . На практике эти два часто обозначаются просто как A .${\displaystyle \mathbf {C} (A,A)}$
• Для всех объектов A , B и C существует функтор , называемый горизонтальной композицией или композицией вдоль 0-клетки , который ассоциативен и допускает ^{[ необходимо разъяснение ]} тождественные 1 и 2-клетки id _A в качестве тождеств. Здесь ассоциативность для означает, что горизонтальное составление дважды в не зависит от того, какой из двух и составлен первым. Символ композиции часто опускается, горизонтальная композиция 2-клеток и записывается просто как .${\displaystyle \circ _{0}\colon \mathbf {C} (B,C)\times \mathbf {C} (A,B)\to \mathbf {C} (A,C)}$${\displaystyle \circ _{0}}$${\displaystyle \mathbf {C} (C,D)\times \mathbf {C} (B,C)\times \mathbf {C} (A,B)}$${\displaystyle \mathbf {C} (A,D)}$${\displaystyle \mathbf {C} (C,D)\times \mathbf {C} (B,C)}$${\displaystyle \mathbf {C} (B,C)\times \mathbf {C} (A,B)}$${\displaystyle \circ _{0}}$${\displaystyle \alpha \colon f\Стрелка вправо g\двоеточие от A\до B}$${\displaystyle \beta \colon f'\Rightarrow g'\colon B\to C}$${\displaystyle \beta \alpha \colon f'f\Стрелка вправо g'g\colon A\to C}$

Терминология 0-клеток , 1-клеток и 2-клеток в некоторых источниках ^[3] заменена на 0-морфизмы , 1-морфизмы и 2-морфизмы (см. также Теория высших категорий ).

Понятие 2-категории отличается от более общего понятия бикатегории тем , что композиция 1-клеток (горизонтальная композиция) должна быть строго ассоциативной, тогда как в бикатегории она должна быть ассоциативной только до 2-изоморфизма. Аксиомы 2-категории являются следствиями их определения как Cat -обогащенных категорий:

• Вертикальная композиция ассоциативна и унитарна, единицами являются тождественные 2-ячейки id _f .
• Горизонтальная композиция также (строго) ассоциативна и унитальна, причем единицами являются тождественные 2-ячейки id _{id A} на тождественных 1-ячейках id _A .
• Закон взаимозаменяемости выполняется; т.е. верно, что для составных 2-клеток${\displaystyle \альфа,\бета,\гамма,\дельта}$

${\displaystyle (\alpha \circ _{0}\beta)\circ _{1}(\gamma \circ _{0}\delta) = (\alpha \circ _{1}\gamma)\circ _{ 0}(\beta \circ _{1}\delta )}$

Закон взаимозамены следует из того факта, что является функтором между категориями hom. Его можно изобразить в виде диаграммы вставки следующим образом:${\displaystyle \circ _{0}}$

	=		=		${\displaystyle \circ _{0}}$
${\displaystyle \circ _{1}}$

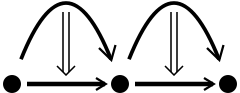Здесь левая диаграмма обозначает вертикальную композицию горизонтальных композитов, правая диаграмма обозначает горизонтальную композицию вертикальных композитов, а диаграмма в центре является обычным представлением обеих. 2-ячейки нарисованы двойными стрелками ⇒, 1-ячейки — одинарными стрелками →, а 0-ячейки — точками.

Категория Ord (предварительно упорядоченных множеств) является 2-категорией, поскольку предварительные множества можно легко интерпретировать как категории.

Архетипическая 2-категория — это категория малых категорий , в которой естественные преобразования служат 2-морфизмами; по этой причине 2-морфизмы обычно обозначаются греческими буквами (как указано выше).${\displaystyle \альфа}$

Объекты ( 0-клетки ) все являются малыми категориями, и для всех объектов A и B категория является функторной категорией . В этом контексте вертикальная композиция является ^[4] композицией естественных преобразований.${\displaystyle \mathbf {C} (A,B)}$

В математике доктрина — это просто 2-категория, которая эвристически рассматривается как система теорий. Например, алгебраические теории , изобретенные Уильямом Ловером , являются примером доктрины, как и многосортные теории, операды , категории и топосы .

Объекты 2-категории называются теориями , 1-морфизмы называются моделями A в B , а 2-морфизмы называются морфизмами между моделями.${\displaystyle f\двоеточие A\rightarrow B}$

Различие между 2-категорией и доктриной на самом деле только эвристическое: обычно не считают, что 2-категория населена теориями как объектами и моделями как морфизмами. Именно этот словарь делает теорию доктрин стоящей.

Например, 2-категория Cat категорий, функторов и естественных преобразований является доктриной. Сразу видно, что все категории предпучка являются категориями моделей.

В качестве другого примера можно взять подкатегорию Cat, состоящую только из категорий с конечными произведениями в качестве объектов и сохраняющими произведения функторами в качестве 1-морфизмов. Это доктрина многосортных алгебраических теорий. Если бы нам нужны были только 1-сортные алгебраические теории, мы бы ограничили объекты только теми категориями, которые генерируются под произведениями одним объектом.

Доктрины были открыты Джонатаном Мок Беком .

• n -категория
• 2-я категория в n Lab

• Обобщенные алгебраические модели , Клаудия Чентаццо.

• Медиа, связанные со Строгой категорией 2 на Wikimedia Commons