Интервальная оценка
В статистике интервальная оценка — это использование выборочных данных для оценки интервала возможных значений интересующего параметра . Это отличается от точечной оценки , которая дает единственное значение. [1 ]
Наиболее распространенными формами интервальной оценки являются доверительные интервалы ( частотный метод) и правдоподобные интервалы ( байесовский метод ). [2] Менее распространенные формы включают в себя интервалы правдоподобия , фидуциальные интервалы , интервалы толерантности и интервалы прогнозирования . Для нестатистического метода интервальные оценки могут быть выведены из нечеткой логики .
Типы
Доверительные интервалы
Доверительные интервалы используются для оценки интересующего параметра из выборочного набора данных, обычно среднего значения или стандартного отклонения . Доверительный интервал утверждает, что существует 100γ% уверенность в том, что интересующий параметр находится в пределах нижней и верхней границы. Распространенное заблуждение относительно доверительных интервалов заключается в том, что 100γ% набора данных укладывается в пределы или выше/ниже границ, это называется интервалом допуска, который обсуждается ниже.
Существует несколько методов построения доверительного интервала, правильный выбор зависит от анализируемых данных. Для нормального распределения с известной дисперсией используется z-таблица для создания интервала, где уровень достоверности 100γ% может быть получен вокруг выборочного среднего из набора данных из n измерений, . Для биномиального распределения доверительные интервалы могут быть аппроксимированы с помощью метода аппроксимации Вальда , интервала Джеффри и интервала Клоппера-Пирсона . Метод Джеффри также может быть использован для аппроксимации интервалов для распределения Пуассона . [3] Если базовое распределение неизвестно, можно использовать бутстреппинг для создания границ вокруг медианы набора данных.
Достоверные интервалы
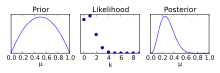
В отличие от доверительного интервала, достоверный интервал требует предварительного предположения, изменения предположения с использованием фактора Байеса и определения апостериорного распределения . Используя апостериорное распределение, можно определить 100γ% вероятность того, что интересующий параметр включен, в отличие от доверительного интервала, где можно быть на 100γ% уверенным , что оценка включена в интервал. [4]
Хотя априорное предположение полезно для предоставления большего количества данных для построения интервала, оно устраняет объективность доверительного интервала. Априорное предположение будет использоваться для информирования апостериорного, если его не оспаривать, это априорное предположение может привести к неверным прогнозам. [5]
Границы доверительного интервала изменчивы, в отличие от доверительного интервала. Существует несколько методов определения того, где должны располагаться правильные верхние и нижние пределы. Распространенные методы корректировки границ интервала включают в себя наивысший апостериорный интервал плотности (HPDI), равнохвостый интервал или выбор центра интервала вокруг среднего значения.
Менее распространенные формы
Основанный на вероятности
Использует принципы функции правдоподобия для оценки интересующего параметра. Используя метод, основанный на правдоподобии, можно найти доверительные интервалы для экспоненциальных, Вейбулла и логнормальных средних. Кроме того, подходы, основанные на правдоподобии, могут дать доверительные интервалы для стандартного отклонения. Также возможно создать интервал прогнозирования, объединив функцию правдоподобия и будущую случайную величину. [3]
Фидуциальный
Фидуциальный вывод использует набор данных, тщательно удаляет шум и восстанавливает оценщик распределения, обобщенное фидуциальное распределение (GFD). Без использования теоремы Байеса нет предположения о предшествующем, во многом подобно доверительным интервалам. Фидуциальный вывод является менее распространенной формой статистического вывода . Основатель, RA Fisher , который разрабатывал методы обратной вероятности, имел свои собственные вопросы о валидности процесса. Хотя фидуциальный вывод был разработан в начале двадцатого века, в конце двадцатого века считали, что метод уступает частотному и байесовскому подходам, но занимает важное место в историческом контексте для статистического вывода. Однако современные подходы обобщили фидуциальный интервал в обобщенный фидуциальный вывод (GFI), который можно использовать для оценки дискретных и непрерывных наборов данных. [6]
Терпимость
Интервалы допуска используют совокупность собранных данных для получения интервала в пределах допуска, содержащего 100γ% значений. Примеры, обычно используемые для описания интервалов допуска, включают производство. В этом контексте процент существующего набора продуктов оценивается, чтобы гарантировать, что процент популяции включен в пределы допуска. При создании интервалов допуска границы могут быть записаны в терминах верхнего и нижнего предела допуска, используя выборочное среднее значение , и выборочное стандартное отклонение , s.
- для двусторонних интервалов
для двусторонних интервалов
А в случае односторонних интервалов, где допуск требуется только выше или ниже критического значения,
варьируется в зависимости от распределения и числа сторон, i, в интервальной оценке. В нормальном распределении может быть выражено как [7]
Где,
- — критическое значение распределения хи-квадрат, использующее степени свободы, которое превышается с вероятностью .
— критические значения, полученные из нормального распределения.
Прогноз
Интервал прогнозирования оценивает интервал, содержащий будущие образцы с некоторой уверенностью, γ. Интервалы прогнозирования могут использоваться как для байесовского , так и для частотного контекста. Эти интервалы обычно используются в наборах данных регрессии, но интервалы прогнозирования не используются для экстраполяции за пределы экспериментально контролируемых параметров предыдущих данных. [8]
Нечеткая логика
Нечеткая логика используется для обработки принятия решений небинарным способом для искусственного интеллекта, медицинских решений и других областей. В общем, она принимает входные данные, сопоставляет их с системами нечеткого вывода и выдает выходное решение. Этот процесс включает в себя фаззификацию, оценку правил нечеткой логики и дефаззификацию. При рассмотрении оценки правил нечеткой логики функции принадлежности преобразуют нашу небинарную входную информацию в осязаемые переменные. Эти функции принадлежности необходимы для прогнозирования неопределенности системы.
Односторонний против двустороннего
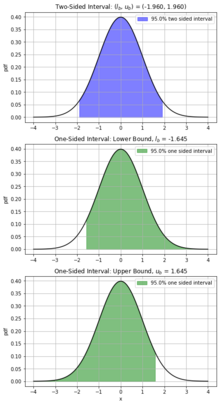
Двусторонние интервалы оценивают интересующий параметр Θ с уровнем достоверности γ, используя нижнюю ( ) и верхнюю границу ( ). Примерами могут служить оценка среднего роста мужчин в географическом регионе или длины конкретного стола, изготовленного производителем. В этих случаях, как правило, оценивается центральное значение параметра. Обычно это представляется в форме, аналогичной уравнению ниже.
В отличие от двустороннего интервала, односторонний интервал использует уровень уверенности γ для построения минимальной или максимальной границы, которая предсказывает интересующий параметр с вероятностью γ*100%. Обычно односторонний интервал требуется, когда минимальная или максимальная граница оценки не представляет интереса. Когда речь идет о минимальном прогнозируемом значении Θ, больше не требуется находить верхнюю границу оценки, что приводит к редуцированной форме двустороннего.
В результате удаления верхней границы и сохранения уверенности нижняя граница ( ) увеличится. Аналогично, когда речь идет о поиске только верхней границы оценки параметра, верхняя граница уменьшится. Односторонний интервал часто встречается в обеспечении качества производства материалов , где ожидаемое значение прочности материала, Θ, должно быть выше определенного минимального значения ( ) с некоторой уверенностью (100γ%). В этом случае производитель не озабочен выпуском слишком прочного продукта, верхней границы ( ) нет .
Обсуждение
При определении статистической значимости параметра лучше всего понимать данные и методы их сбора. Перед сбором данных эксперимент должен быть спланирован таким образом, чтобы ошибка выборки была статистической изменчивостью ( случайной ошибкой ), а не статистическим смещением ( систематической ошибкой ). [9] После эксперимента типичным первым шагом в создании интервальных оценок является построение исследовательского анализа с использованием различных графических методов . Из этого можно определить распределение выборок из набора данных. Создание границ интервала с неверными предположениями на основе распределения делает прогноз неверным. [10]
Когда сообщаются интервальные оценки, они должны иметь общепринятую интерпретацию внутри и за пределами научного сообщества. Интервальные оценки, полученные из нечеткой логики, имеют гораздо больше прикладных значений.
В часто встречающихся ситуациях должны быть наборы стандартных процедур, которые могут быть использованы при условии проверки и обоснованности любых требуемых предположений. Это применимо как к доверительным интервалам, так и к вероятным интервалам. Однако в более новых ситуациях должны быть указания о том, как можно формулировать оценки интервалов. В этом отношении доверительные интервалы и вероятные интервалы имеют схожее положение, но есть два различия. Во-первых, вероятные интервалы могут легко иметь дело с предшествующей информацией, в то время как доверительные интервалы не могут. Во-вторых, доверительные интервалы более гибкие и могут использоваться на практике в большем количестве ситуаций, чем вероятные интервалы: одна область, где вероятные интервалы страдают в сравнении, — это работа с непараметрическими моделями .
Должны быть способы проверки производительности процедур интервальной оценки. Это возникает, поскольку многие такие процедуры включают приближения различных видов, и необходимо проверить, что фактическая производительность процедуры близка к заявленной. Использование стохастического моделирования делает это простым в случае доверительных интервалов, но это несколько более проблематично для достоверных интервалов, где априорная информация должна быть должным образом учтена. Проверка достоверных интервалов может быть выполнена для ситуаций, представляющих отсутствие априорной информации, но проверка включает проверку долгосрочных частотных свойств процедур.
Северини (1993) обсуждает условия, при которых достоверные интервалы и доверительные интервалы будут давать схожие результаты, а также обсуждает как вероятности покрытия достоверных интервалов, так и апостериорные вероятности, связанные с доверительными интервалами. [11]
В теории принятия решений , которая является общим подходом и обоснованием байесовской статистики, интервальная оценка не представляет прямого интереса. Результатом является решение, а не интервальная оценка, и поэтому сторонники байесовской теории принятия решений используют байесовское действие : они минимизируют ожидаемые потери функции потерь относительно всего апостериорного распределения, а не конкретного интервала.
Приложения
Применение доверительных интервалов используется для решения различных проблем, связанных с неопределенностью. Katz (1975) предлагает различные проблемы и преимущества использования интервальных оценок в судебных разбирательствах. [12] Для использования в медицинских исследованиях Altmen (1990) обсуждает использование доверительных интервалов и руководящие принципы по их использованию. [13] В производстве также часто встречаются интервальные оценки, оценивающие срок службы продукта или допуски продукта. Meeker и Escobar (1998) представляют методы анализа данных о надежности при параметрической и непараметрической оценке, включая прогнозирование будущих случайных величин (прогнозные интервалы). [14]
Смотрите также
- Правило 68–95–99.7
- Алгоритмический вывод
- Проблема Беренса–Фишера сыграла важную роль в развитии теории, лежащей в основе применяемых статистических методологий.
- Вероятность покрытия
- Статистика оценок
- Индукция (философия)
- Допустимая погрешность
- Множественные сравнения
- Философия статистики
- Предиктивный вывод
- Статистическое вмешательство
Ссылки
- ^ Нейман, Дж. (1937). «Очерк теории статистической оценки, основанной на классической теории вероятностей». Философские труды Лондонского королевского общества. Серия A, Математические и физические науки . 236 (767). Королевское общество: 333–380 . Bibcode : 1937RSPTA.236..333N. doi : 10.1098/rsta.1937.0005 . ISSN 0080-4614. JSTOR 91337. S2CID 19584450. Получено 15 июля 2021 г.
- ^ Северини, Томас А. (1991). «О связи между байесовскими и небайесовскими интервальными оценками». Журнал Королевского статистического общества, Серия B (Методологическая) . 53 (3). Wiley: 611– 618. doi :10.1111/j.2517-6161.1991.tb01849.x. ISSN 0035-9246.
- ^ ab Meeker, William Q.; Hahn, Gerald J.; Escobar, Luis A. (2017-03-27). Статистические интервалы: руководство для практиков и исследователей . Wiley Series in Probability and Statistics (1-е изд.). Wiley. doi :10.1002/9781118594841. ISBN 978-0-471-68717-7.
- ^ Хеспаньол, Луис; Валлио, Кайо Сайн; Коста, Лусиола Менезес; Сараджиотто, Бруно Т (2019-07-01). «Понимание и интерпретация достоверности и достоверных интервалов вокруг оценок эффекта». Бразильский журнал физиотерапии . 23 (4): 290– 301. doi : 10.1016 /j.bjpt.2018.12.006. ISSN 1413-3555. PMC 6630113. PMID 30638956.
- ^ Ли, Питер М. (2012). Байесовская статистика: введение (4-е изд., 1-е изд.). Чичестер: Wiley. ISBN 978-1-118-33257-3.
- ^ Ханниг, Ян; Айер, Хари; Лай, Рэнди CS; Ли, Томас CM (2016-07-02). «Обобщенный фидуциальный вывод: обзор и новые результаты». Журнал Американской статистической ассоциации . 111 (515): 1346– 1361. doi :10.1080/01621459.2016.1165102. ISSN 0162-1459.
- ^ Howe, WG (июнь 1969). «Двусторонние пределы толерантности для нормальной популяции, некоторые улучшения». Журнал Американской статистической ассоциации . 64 (326): 610. doi :10.2307/2283644. ISSN 0162-1459.
- ^ Вардеман, Стивен Б. (1992). «Что насчет других интервалов?». The American Statistician . 46 (3): 193– 197. doi :10.2307/2685212. ISSN 0003-1305.
- ^ Хан, Джеральд Дж.; Микер, Уильям К. (1993). «Предположения для статистического вывода». Американский статистик . 47 (1): 1– 11. doi :10.2307/2684774. ISSN 0003-1305.
- ^ Хан, Джеральд Дж.; Доганаксой, Неджип; Микер, Уильям К. (01.08.2019). «Статистические интервалы, а не статистическая значимость». Значимость . 16 (4): 20–22 . doi : 10.1111/j.1740-9713.2019.01298.x . ISSN 1740-9705.
- ^ Северини, Томас А. (1993). «Байесовские интервальные оценки, которые также являются доверительными интервалами». Журнал Королевского статистического общества. Серия B (Методологическая) . 55 (2): 533– 540. ISSN 0035-9246.
- ^ Кац, Лео (1975). «Представление оценки доверительного интервала в качестве доказательства в судебном разбирательстве». The American Statistician . 29 (4): 138– 142. doi :10.2307/2683480. ISSN 0003-1305.
- ^ Альтман, Дуглас Г., ред. (2011). Статистика с уверенностью: доверительные интервалы и статистические рекомендации; [включает диск] (2-е изд., [Nachdr.] ред.). Лондон: BMJ Books. ISBN 978-0-7279-1375-3.
- ^ Микер, Уильям К.; Эскобар, Луис А. (1998). Статистические методы для данных надежности . Ряды Wiley в вероятности и статистике. Раздел прикладной вероятности и статистики. Нью-Йорк Вайнхайм: Wiley. ISBN 978-0-471-14328-4.
Библиография
- Кендалл, МГ и Стюарт, А. (1973). Продвинутая теория статистики. Том 2: Вывод и взаимосвязь (3-е издание). Гриффин, Лондон.
- В главе 20 выше рассматриваются доверительные интервалы, а в главе 21 рассматриваются фидуциальные интервалы и байесовские интервалы , а также обсуждается сравнение трех подходов. Обратите внимание, что эта работа предшествует современным вычислительно-интенсивным методологиям. Кроме того, в главе 21 обсуждается проблема Беренса–Фишера.
- Микер, В. К., Хан, Г. Дж. и Эскобар, Л. А. (2017). Статистические интервалы: руководство для практиков и исследователей (2-е издание). John Wiley & Sons.
Внешние ссылки
- Введение в нечеткую математику https://web.archive.org/web/20061205114153/http://blog.peltarion.com/2006/10/25/fuzzy-math-part-1-the-theory
- Что такое нечеткая логика? https://www.youtube.com/watch?v=__0nZuG4sTw
















