Статистическая теория обучения

Фреймворк для машинного обучения

Статистическая теория обучения — это структура для машинного обучения, основанная на статистике и функциональном анализе . ^[1]^[2]^[3] Статистическая теория обучения занимается проблемой статистического вывода для нахождения предсказательной функции на основе данных. Статистическая теория обучения привела к успешным приложениям в таких областях, как компьютерное зрение , распознавание речи и биоинформатика .

Введение

Целями обучения являются понимание и прогнозирование. Обучение делится на множество категорий, включая контролируемое обучение , неконтролируемое обучение , онлайн-обучение и обучение с подкреплением . С точки зрения статистической теории обучения контролируемое обучение лучше всего понимается. ^[4] Контролируемое обучение включает обучение на обучающем наборе данных. Каждая точка обучения представляет собой пару вход-выход, где вход сопоставляется с выходом. Задача обучения состоит в выводе функции, которая сопоставляет вход и выход, так что изученная функция может использоваться для прогнозирования выхода из будущего входа.

В зависимости от типа выходных данных, контролируемые проблемы обучения являются либо проблемами регрессии , либо проблемами классификации . Если выходные данные принимают непрерывный диапазон значений, то это проблема регрессии. Используя закон Ома в качестве примера, регрессия может быть выполнена с напряжением в качестве входных данных и током в качестве выходных данных. Регрессия обнаружит функциональную связь между напряжением и током , такую, что Проблемы классификации — это те, для которых выходные данные будут элементом из дискретного набора меток. Классификация очень распространена в приложениях машинного обучения. Например, в распознавании лиц изображение лица человека будет входными данными, а выходной меткой будет имя этого человека. Входные данные будут представлены большим многомерным вектором, элементы которого представляют пиксели на изображении. $R$ $V=IR$

После обучения функции на основе данных обучающего набора эта функция проверяется на тестовом наборе данных, которые не встречались в обучающем наборе.

Формальное описание

Возьмем в качестве векторного пространства всех возможных входов, а в качестве векторного пространства всех возможных выходов. Статистическая теория обучения исходит из того, что существует некоторое неизвестное распределение вероятностей по пространству произведений , т. е. существует некоторое неизвестное . Обучающий набор состоит из выборок из этого распределения вероятностей и обозначается следующим образом: Каждый — это входной вектор из обучающих данных, а — это соответствующий ему выход. $X$ $Y$ $Z=X\times Y$ $p(z)=p(\mathbf {x} ,y)$ $n$ $S=\{(\mathbf {x} _{1},y_{1}),\dots ,(\mathbf {x} _{n},y_{n})\}=\{\mathbf {z} _{1},\dots ,\mathbf {z} _{n}\}$ $\mathbf {x} _{i}$ $y_{i}$

В этом формализме задача вывода состоит в нахождении функции такой, что . Пусть будет пространством функций, называемым пространством гипотез. Пространство гипотез — это пространство функций, в котором алгоритм будет производить поиск. Пусть будет функцией потерь , метрикой для разницы между предсказанным значением и фактическим значением . Ожидаемый риск определяется как Целевая функция, наилучшая возможная функция , которую можно выбрать, задается как , которая удовлетворяет $f:X\to Y$ $f(\mathbf {x} )\sim y$ ${\mathcal {H}}$ $f:X\to Y$ $V(f(\mathbf {x} ),y)$ $f(\mathbf {x} )$ $y$ $I[f]=\int _{X\times Y}V(f(\mathbf {x} ),y)\,p(\mathbf {x} ,y)\,d\mathbf {x} \,dy$ $f$ $f$ $f=\mathop {\operatorname {argmin} } _{h\in {\mathcal {H}}}I[h]$

Поскольку распределение вероятностей неизвестно, необходимо использовать прокси-меру для ожидаемого риска. Эта мера основана на обучающем наборе, образце из этого неизвестного распределения вероятностей. Она называется эмпирическим риском. Алгоритм обучения, который выбирает функцию , минимизирующую эмпирический риск, называется минимизацией эмпирического риска . $p(\mathbf {x} ,y)$ $I_{S}[f]={\frac {1}{n}}\sum _{i=1}^{n}V(f(\mathbf {x} _{i}),y_{i})$ $f_{S}$

Функции потерь

Выбор функции потерь является определяющим фактором для функции , которая будет выбрана алгоритмом обучения. Функция потерь также влияет на скорость сходимости алгоритма. Важно, чтобы функция потерь была выпуклой . ^[5] $f_{S}$

В зависимости от того, является ли проблема проблемой регрессии или классификации, используются различные функции потерь.

Регрессия

Наиболее распространенной функцией потерь для регрессии является квадратичная функция потерь (также известная как L2-норма ). Эта знакомая функция потерь используется в регрессии по методу наименьших квадратов . Форма: $V(f(\mathbf {x} ),y)=(y-f(\mathbf {x} ))^{2}$

Иногда также используется абсолютная потеря значения (также известная как норма L1 ): $V(f(\mathbf {x} ),y)=|y-f(\mathbf {x} )|$

Классификация

В некотором смысле функция индикатора 0-1 является наиболее естественной функцией потерь для классификации. Она принимает значение 0, если прогнозируемый выход совпадает с фактическим выходом, и принимает значение 1, если прогнозируемый выход отличается от фактического выхода. Для бинарной классификации с это: где — ступенчатая функция Хевисайда . $Y=\{-1,1\}$ $V(f(\mathbf {x} ),y)=\theta (-yf(\mathbf {x} ))$ $\theta$

Регуляризация

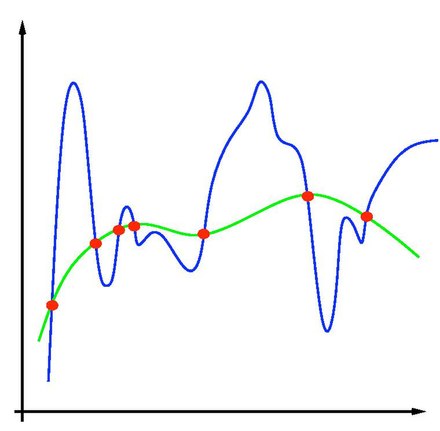
В задачах машинного обучения возникает одна из основных проблем — переобучение . Поскольку обучение — это задача прогнозирования, цель состоит не в том, чтобы найти функцию, которая наиболее точно соответствует (ранее наблюдаемым) данным, а в том, чтобы найти функцию, которая будет наиболее точно предсказывать выходные данные из будущих входных данных. Минимизация эмпирического риска сопряжена с этим риском переобучения: нахождение функции, которая точно соответствует данным, но плохо предсказывает будущие выходные данные.

Переобучение является симптомом нестабильных решений; небольшое возмущение в данных обучающего набора вызовет большую вариацию в обученной функции. Можно показать, что если стабильность решения может быть гарантирована, то обобщение и согласованность также гарантированы. ^[6]^[7] Регуляризация может решить проблему переобучения и придать проблеме устойчивость.

Регуляризация может быть достигнута путем ограничения пространства гипотез . Обычным примером будет ограничение линейными функциями: это можно рассматривать как сведение к стандартной задаче линейной регрессии . также может быть ограничено полиномами степени , экспоненциальными функциями или ограниченными функциями на L1 . Ограничение пространства гипотез позволяет избежать переобучения, поскольку форма потенциальных функций ограничена и, таким образом, не позволяет выбрать функцию, которая дает эмпирический риск произвольно близко к нулю. ${\mathcal {H}}$ ${\mathcal {H}}$ ${\mathcal {H}}$ $p$

Одним из примеров регуляризации является регуляризация Тихонова . Она заключается в минимизации , где — фиксированный и положительный параметр, параметр регуляризации. Регуляризация Тихонова обеспечивает существование, единственность и устойчивость решения. ^[8] ${\frac {1}{n}}\sum _{i=1}^{n}V(f(\mathbf {x} _{i}),y_{i})+\gamma \left\|f\right\|_{\mathcal {H}}^{2}$ $\gamma$

Ограничение эмпирического риска

Рассмотрим бинарный классификатор . Мы можем применить неравенство Хеффдинга , чтобы ограничить вероятность того, что эмпирический риск отклоняется от истинного риска, чтобы быть субгауссовым распределением . Но, как правило, когда мы минимизируем эмпирический риск, нам не дается классификатор; мы должны выбрать его. Поэтому более полезным результатом будет ограничение вероятности супремума разности по всему классу. где — дробящее число , а — количество образцов в вашем наборе данных. Экспоненциальный член взят из Хеффдинга, но есть дополнительные затраты на взятие супремума по всему классу, что является дробящим числом. $f:{\mathcal {X}}\to \{0,1\}$ $\mathbb {P} (|{\hat {R}}(f)-R(f)|\geq \epsilon )\leq 2e^{-2n\epsilon ^{2}}$ $\mathbb {P} {\bigg (}\sup _{f\in {\mathcal {F}}}|{\hat {R}}(f)-R(f)|\geq \epsilon {\bigg )}\leq 2S({\mathcal {F}},n)e^{-n\epsilon ^{2}/8}\approx n^{d}e^{-n\epsilon ^{2}/8}$ $S({\mathcal {F}},n)$ $n$

Смотрите также

Воспроизводящие ядра Гильбертовы пространства являются полезным выбором для . ${\mathcal {H}}$
Методы проксимального градиента для обучения
сложность Радемахера
Размерность Вапника–Червоненкиса

Ссылки

^ Вапник, Владимир Н. (1995). Природа статистической теории обучения . Нью-Йорк: Springer. ISBN 978-1-475-72440-0.
^ Хасти, Тревор ; Тибширани, Роберт; Фридман, Джером Х. (2009). Элементы статистического обучения: добыча данных, вывод и прогнозирование . Springer Series in Statistics. Нью-Йорк, штат Нью-Йорк: Springer. ISBN 978-0-387-84857-0.
^ Mohri, Mehryar ; Rostamizadeh, Afshin; Talwalkar, Ameet (2012). Основы машинного обучения . США, Массачусетс: MIT Press. ISBN 9780262018258.
^ Томазо Поджио, Лоренцо Росаско и др. Статистическая теория обучения и ее применение , 2012, класс 1
^ Росаско, Лоренцо; Де Вито, Эрнесто; Капоннетто, Андреа; Пиана, Мишель; Верри, Алессандро (1 мая 2004 г.). «Все ли функции потерь одинаковы?». Нейронные вычисления . 16 (5): 1063–1076 . doi : 10.1162/089976604773135104. ISSN 0899-7667. ПМИД 15070510.
^ Вапник, В. Н. и Червоненкис, А. Ю. 1971. О равномерной сходимости относительных частот событий к их вероятностям. Теория вероятностей и ее приложения, т. 16, стр. 264-280.
^ Мукерджи, С., Ниёги, П., Поджио, Т. и Рифкин, Р. 2006. Теория обучения: стабильность достаточна для обобщения и необходима и достаточна для согласованности минимизации эмпирического риска. Успехи вычислительной математики . Том 25, стр. 161-193.
^ Томазо Поджио, Лоренцо Росаско и др. Статистическая теория обучения и ее применение , 2012, класс 2

[1] Вапник, Владимир Н. (1995). Природа статистической теории обучения . Нью-Йорк: Springer. ISBN 978-1-475-72440-0.

[2] Хасти, Тревор ; Тибширани, Роберт; Фридман, Джером Х. (2009). Элементы статистического обучения: добыча данных, вывод и прогнозирование . Springer Series in Statistics. Нью-Йорк, штат Нью-Йорк: Springer. ISBN 978-0-387-84857-0.

[3] Mohri, Mehryar ; Rostamizadeh, Afshin; Talwalkar, Ameet (2012). Основы машинного обучения . США, Массачусетс: MIT Press. ISBN 9780262018258.

[4] Томазо Поджио, Лоренцо Росаско и др. Статистическая теория обучения и ее применение , 2012, класс 1

[5] Росаско, Лоренцо; Де Вито, Эрнесто; Капоннетто, Андреа; Пиана, Мишель; Верри, Алессандро (1 мая 2004 г.). «Все ли функции потерь одинаковы?». Нейронные вычисления . 16 (5): 1063–1076 . doi : 10.1162/089976604773135104. ISSN 0899-7667. ПМИД 15070510.

[6] Вапник, В. Н. и Червоненкис, А. Ю. 1971. О равномерной сходимости относительных частот событий к их вероятностям. Теория вероятностей и ее приложения, т. 16, стр. 264-280.

[7] Мукерджи, С., Ниёги, П., Поджио, Т. и Рифкин, Р. 2006. Теория обучения: стабильность достаточна для обобщения и необходима и достаточна для согласованности минимизации эмпирического риска. Успехи вычислительной математики . Том 25, стр. 161-193.

[8] Томазо Поджио, Лоренцо Росаско и др. Статистическая теория обучения и ее применение , 2012, класс 2