Решётчатый граф

В теории графов решетчатый граф , сетчатый граф или решетчатый граф — это граф , рисунок которого , вложенный в некоторое евклидово пространство ⁠ ⁠${\displaystyle \mathbb {R} ^{n}}$ , образует регулярную мозаику . Это подразумевает, что группа биективных преобразований , отправляющих граф в себя, является решеткой в ​​теоретико-групповом смысле .

Обычно не делается четкого различия между таким графом в более абстрактном смысле теории графов и его изображением в пространстве (часто на плоскости или в трехмерном пространстве). Этот тип графа можно короче назвать просто решеткой , сеткой или сеткой . Более того, эти термины также обычно используются для конечного сечения бесконечного графа, как в «квадратной сетке 8 × 8».

Термин «решетчатый граф» также использовался в литературе для обозначения различных других видов графов с некоторой регулярной структурой, таких как декартово произведение ряда полных графов . ^[1]

Распространенным типом решетчатого графа (известного под разными названиями, такими как граф сетки или граф квадратной сетки ) является граф, вершины которого соответствуют точкам на плоскости с целочисленными координатами, причем координаты x находятся в диапазоне 1, ...,  n , координаты y находятся в диапазоне 1, ...,  m , и две вершины соединены ребром всякий раз, когда соответствующие точки находятся на расстоянии 1. Другими словами, это граф единичных расстояний для целочисленных точек в прямоугольнике со сторонами, параллельными осям. ^[2]

Граф квадратной сетки является декартовым произведением графов , а именно двух графов путей с n  − 1 и m  − 1 ребрами. ^[2] Поскольку граф путей является медианным графом , последний факт подразумевает, что граф квадратной сетки также является медианным графом. Все графы квадратной сетки являются двудольными , что легко проверяется тем фактом, что можно раскрасить вершины в шахматном порядке.

Граф пути — это граф сетки на сетке. Граф сетки — это 4-цикл . ^[2]${\displaystyle 1\times n}$${\displaystyle 2\times 2}$

Каждый планарный граф H является минором сетки h  ×  h , где . ^[3]${\displaystyle h=2|V(H)|+4|E(H)|}$

Графы сетки являются фундаментальными объектами в теории миноров графов из-за теоремы об исключении сетки . Они играют важную роль в теории двумерности .

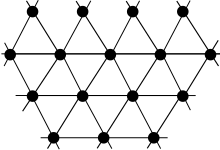
Треугольный сетчатый график — это график, соответствующий треугольной сетке.

Граф сетки Ханана для конечного набора точек на плоскости создается сеткой, полученной пересечением всех вертикальных и горизонтальных линий, проходящих через каждую точку набора.

Граф ладьи (граф, который представляет все допустимые ходы шахматной фигуры ладьи на шахматной доске ) также иногда называют графом решетки , хотя этот граф отличается от графа решетки, описанного здесь, поскольку все точки в одной строке или столбце являются смежными. Допустимые ходы шахматной фигуры фей вазира образуют граф квадратной решетки.

• Решетчатый путь
• Теорема Пика
• Целочисленные треугольники в двумерной решетке
• Регулярный график