Площадь оппозиции


В терминологии логики (раздел философской логики ) квадрат оппозиции — это диаграмма , представляющая отношения между четырьмя основными категорическими суждениями . Происхождение квадрата можно проследить до трактата Аристотеля « Об истолковании» и его различия между двумя оппозициями: противоречием и противоположностью . Однако Аристотель не рисовал никакой диаграммы; это сделали несколько столетий спустя Апулей и Боэций .
Краткое содержание
В традиционной логике предложение (лат. propositio ) — это устное утверждение ( oratio enunciativa ), а не значение утверждения, как в современной философии языка и логики . Категорическое предложение — это простое предложение, содержащее два термина: субъект ( S ) и предикат ( P ), в котором предикат либо утверждается, либо отрицается относительно субъекта.
Каждое категорическое суждение может быть сведено к одной из четырех логических форм , называемых A , E , I и O, основанных на латинском affirmo ( я утверждаю ) для утвердительных суждений A и I и n e g o (я отрицаю) для отрицательных суждений E и O. Это:
- Предложение А , общеутвердительное ( universalis assertativa ), форма которого на латыни — «omne S est P », обычно переводится как «всякое S есть P ».
- Суждение E , общеотрицательное ( universalis negativa ), латинская форма «nullum S est P », обычно переводится как «ни одно S не есть P ».
- Предложение I , частное утвердительное предложение ( specialisafferativa ), латинское «quoddam S est P », обычно переводимое как «некоторые S есть P ».
- Предложение О , частное отрицание ( партикулярис негатива ), латинское «quoddam S nōn est P », обычно переводится как «некоторые S не являются P ».
В табличной форме:
| Имя | Символ | латинский | Английский* | Мнемонический | Современная форма [1] |
|---|---|---|---|---|---|
| Универсальный утвердительный | А | Омне Сест П. | Каждое S есть P. ( S всегда есть P. ) | a ffirmo (я утверждаю) | |
| Универсальный отрицательный | Э | Нуллум Сест П. | Ни одно S не является P. ( S никогда не является P. ) | н е г о (я отрицаю) | |
| Частное утвердительное | я | Куоддам Сест П. | Некоторые S есть P. ( Иногда S есть P. ) | aff i rmo (я утверждаю) | |
| Конкретный негатив | О | Куоддам С. не является П. | Некоторые S не являются P. ( S не всегда является P. ) | отрицаю ( отрицаю ) |
* Предложение A может быть сформулировано как «Все S есть P ». Однако предложение E , сформулированное соответственно как «Все S не есть P », является неоднозначным [2], поскольку оно может быть как предложением E , так и предложением O , поэтому для определения формы требуется контекст; стандартная форма «Ни одно S не есть P » является однозначной, поэтому она предпочтительнее. Предложение O также принимает формы «Иногда S не есть P » и «Определенное S не есть P » (дословно латинское «Quoddam S nōn est P »).
** в современных формах означает, что утверждение применяется к объекту . Во многих случаях его можно просто интерпретировать как " is ". также можно записать как .
Аристотель утверждает (в главах шестой и седьмой Peri hermēneias (Περὶ Ἑρμηνείας, лат. De Interpretatione , англ. «Об толковании»)), что между этими четырьмя видами суждений существуют определенные логические связи. Он говорит, что каждому утверждению соответствует ровно одно отрицание, и что каждое утверждение и его отрицание «противоположны» так, что всегда одно из них должно быть истинным, а другое ложным. Пару утвердительного утверждения и его отрицания он называет « противоречие » (в средневековой латыни, contrastio ). Примерами противоречий являются «каждый человек белый» и «не каждый человек белый» (также читается как «некоторые люди не белые»), «ни один человек не белый» и «некоторый человек белый».
Нижеприведенные отношения, противоположное, подпротивное, подчиненное чередование и сверхчередование, выполняются на основе традиционного логического предположения, что существуют вещи, обозначенные как S (или вещи, удовлетворяющие утверждению S в современной логике). Если это предположение убрать, то эти отношения не выполняются.
« Противоположные » (средневековое: contrariae ) утверждения — это такие утверждения, что оба утверждения не могут быть истинными одновременно. Примерами этого являются всеобщее утвердительное «каждый человек белый» и всеобщее отрицательное «ни один человек не белый». Они не могут быть истинными одновременно. Однако они не являются противоречащими, потому что оба они могут быть ложными. Например, ложно, что каждый человек белый, так как некоторые люди не белые. Однако также ложно, что ни один человек не белый, так как есть некоторые белые люди.
Поскольку каждое утверждение имеет противоречивую противоположность (свое отрицание), и поскольку противоречивое утверждение истинно, когда его противоположность ложна, то отсюда следует, что противоположности противоположностей (которые средневековые люди называли подпротивоположностями , subcontrariae ) могут быть обе истинными, но не могут быть обе ложными. Поскольку подпротивоположности являются отрицаниями универсальных утверждений, средневековые логики называли их «частными» утверждениями.
Другое логическое отношение, подразумеваемое этим, хотя и не упомянутое явно Аристотелем, — это «чередование» ( alternatio ), состоящее из « подчинения » и « сверхчередования ». Подчинение — это отношение между частным утверждением и всеобщим утверждением того же качества (утвердительного или отрицательного), при котором частное подразумевается всеобщим, в то время как сверхчередование — это отношение между ними, при котором ложность всеобщего (что эквивалентно отрицанию всеобщего) подразумевается ложностью частного (что эквивалентно отрицанию частного). [3] (Сверхчередование — это контрапозитив подчинения.) В этих отношениях частное является подчиненным всеобщего, которое является сверхчередованием частного. Например, если «все люди белые» истинно, то его противоположность «ни один человек не белый» ложна. Следовательно, противоречивое «некоторый человек белый» истинно. Аналогично универсальное утверждение «ни один человек не является белым» подразумевает частное утверждение «не каждый человек является белым». [4] [5]
В итоге:
- Универсальные утверждения противоположны: «всякий человек справедлив» и «ни один человек не справедлив» не могут быть истинными вместе, хотя одно из них может быть истинным, а другое ложным, а также оба могут быть ложными (если хотя бы один человек справедлив, а хотя бы один — нет).
- Частные утверждения являются подпротивоположностями. «Некоторый человек справедлив» и «некоторый человек несправедлив» не могут быть ложными вместе.
- Частное утверждение одного качества является подчиненным универсального утверждения того же качества, которое является суперальтерном частного утверждения, потому что в аристотелевской семантике «каждый A есть B » подразумевает «некоторые A есть B », а «никакой A есть B » подразумевает «некоторые A не есть B ». Обратите внимание, что современные формальные интерпретации английских предложений интерпретируют «каждый A есть B » как «для любого x утверждение, что x есть A, подразумевает утверждение, что x есть B », что не подразумевает «некоторые x есть A» . Однако это вопрос семантической интерпретации и не означает, как иногда утверждают, что аристотелевская логика «неверна».
- Общеутвердительное ( A ) и частное отрицание ( O ) противоречат друг другу. Если некоторое A не есть B , то не каждое A есть B. И наоборот, хотя это и не так в современной семантике, считалось, что если каждое A не есть B , то некоторое A не есть B. Такая интерпретация вызвала трудности (см. ниже). В то время как греческий язык Аристотеля не представлял частное отрицание как «некоторое A не есть B» , а как «не каждое A есть B », кто-то в своем комментарии к Peri hermaneias передает частное отрицание как «quoddam A nōn est B », буквально «некое A не есть B », и во всех средневековых сочинениях по логике принято представлять частное предложение таким образом.
Эти отношения стали основой диаграммы, берущей начало от Боэция и использовавшейся средневековыми логиками для классификации логических отношений. Предложения помещаются в четыре угла квадрата, а отношения представляются в виде линий, проведенных между ними, откуда и название «Квадрат оппозиции». Таким образом, можно привести следующие случаи: [6]
- Если A истинно, то E ложно, I истинно, O ложно;
- Если E истинно, то A ложно, I ложно, O истинно;
- Если I истинно, то E ложно, A и O неопределенны;
- Если O истинно, то A ложно, E и I неопределенны;
- Если A ложно, то O истинно, E и I неопределенны;
- Если E ложно, то I истинно, A и O неопределенны;
- Если I ложно, то A ложно, E истинно, O истинно;
- Если O ложно, то A истинно, E ложно, I истинно.
Чтобы запомнить их, средневековые люди придумали следующую латинскую рифму: [7]
- A adfirmat, negat E , sed Universaliter ambae;
Я тверд, отрицаю О , sed частное амбае.
Он утверждает, что A и E не являются ни оба истинными, ни оба ложными в каждом из вышеперечисленных случаев. То же самое относится к I и O. В то время как первые два являются универсальными утверждениями, пара I / O относится к частным.
Квадрат противоположностей использовался для категорических выводов, описанных греческим философом Аристотелем: конверсия , обверсия и контрапозиция . Каждый из этих трех типов категорического вывода применялся к четырем боэтовским логическим формам: A , E , I и O.
Проблема экзистенциального импорта
Субпротивоположности ( I и O ), которые средневековые логики представляли в форме «quoddam A est B » (некоторое конкретное A есть B ) и «quoddam A non est B » (некоторое конкретное A не есть B ), не могут быть оба ложными, поскольку их универсальные противоречивые утверждения (никакое A не есть B / каждое A есть B ) не могут быть оба истинными. Это приводит к затруднению, впервые выявленному Пьером Абеляром (1079 – 21 апреля 1142). «Некоторое A есть B », по-видимому, подразумевает «что-то есть A », другими словами, существует что-то, что есть A. Например, «Некоторый человек белый», по-видимому, подразумевает, что по крайней мере одна существующая вещь — это человек, а именно человек, который должен быть белым, если утверждение «некоторый человек белый» истинно. Но «некоторый человек не белый» также подразумевает, что нечто как человек существует, а именно человек, который не является белым, если утверждение «некоторый человек не белый» истинно. Но аристотелевская логика требует, чтобы одно из этих утверждений (в более общем смысле «некое конкретное A есть B » и «некое конкретное A не есть B ») было истинным, т. е. они не могут быть оба ложными. Следовательно, поскольку оба утверждения подразумевают наличие по крайней мере одной вещи, которая является человеком, то следует присутствие человека или людей. Но, как указывает Абеляр в « Диалектике» , разве люди не могут существовать? [8]
- Ибо, поскольку абсолютно не существует ни одного человека, ни утверждение «каждый человек есть человек», ни утверждение «некоторый человек не есть человек» не являются истинными. [9]
Абеляр также указывает, что подпредложения, содержащие ничего не обозначающие подлежащие термины, такие как «человек, который есть камень», оба являются ложными.
- Если «каждый человек-камень есть камень» истинно, то и его преобразование per accidens истинно («некоторые камни есть люди-камень»). Но ни один камень не есть человек-камень, потому что ни этот человек, ни тот человек и т. д. не есть камень. Но и это «некоторый человек-камень не есть камень» ложно по необходимости, так как невозможно предположить, что оно истинно. [10]
Теренс Парсонс (родился в 1939 году) утверждает, что древние философы не сталкивались с проблемой экзистенциального значения , поскольку только формы A (универсальная утвердительная) и I (частная утвердительная) имели экзистенциальное значение. (Если утверждение включает термин, такой что утверждение ложно, если термин не имеет примеров, т. е. не существует ничего, связанного с термином, то говорят, что утверждение имеет экзистенциальное значение по отношению к этому термину.)
- Утверждения имеют экзистенциальное значение, а отрицания — нет. Таким образом, древние не видели непоследовательности квадрата, как ее сформулировал Аристотель, потому что не было никакой непоследовательности, которую можно было бы увидеть. [11]
Далее он цитирует средневекового философа Вильгельма Мёрбеке (1215–35 – ок. 1286 ):
- В утвердительных предложениях термин всегда утверждается как предполагающий что-то. Таким образом, если он не предполагает ничего, предложение ложно. Однако в отрицательных предложениях утверждение заключается либо в том, что термин не предполагает что-то, либо в том, что он предполагает что-то, предикат чего действительно отрицается. Таким образом, отрицательное предложение имеет две причины истинности. [12]
И указывает на то, что перевод Боэцием труда Аристотеля породил ошибочное представление о том, что форма О имеет экзистенциальное значение.
- Но когда Боэций (477 – 524 н.э.) комментирует этот текст, он иллюстрирует учение Аристотеля с помощью ныне известной диаграммы и использует формулировку «Некоторые люди не справедливы». Так что это, должно быть, показалось ему естественным эквивалентом на латыни. Для нас это выглядит странно на английском языке, но его это не беспокоило. [13]
Современные площади оппозиции
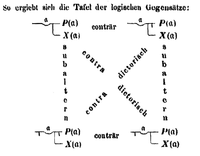
ниже является опечаткой: следует читать subconträr .
В 19 веке Джордж Буль (ноябрь 1815 г. – 8 декабря 1864 г.) выступал за требование экзистенциального значения для обоих терминов в частных утверждениях ( I и O ), но допускал отсутствие экзистенциального значения для всех терминов универсальных утверждений ( A и E ). Это решение сделало диаграммы Венна особенно удобными для использования в логике терминов. Квадрат оппозиции при этом булевом наборе предположений часто называют современным Квадратом оппозиции . В современном квадрате оппозиции утверждения A и O являются противоречивыми, как и E и I , но все другие формы оппозиции перестают иметь место; нет никаких противоречий, подпротиворечий, подчиненных и суперчередований. Таким образом, с современной точки зрения часто имеет смысл говорить о «самой» оппозиции утверждения, а не настаивать, как это делали старые логики, на том, что утверждение имеет несколько различных противоположностей, которые находятся в различных видах оппозиции с утверждением.
В «Begriffsschrift» Готлоба Фреге (8 ноября 1848 г. – 26 июля 1925 г.) также представлен квадрат оппозиций, организованный почти идентично классическому квадрату, показывающий противоречия, подчиненные и противоположности между четырьмя формулами, построенными на основе всеобщей квантификации, отрицания и импликации.
Семиотический квадрат Альгирдаса Жюльена Греймаса (9 марта 1917 г. – 27 февраля 1992 г.) был заимствован из трудов Аристотеля.
Традиционный квадрат оппозиции теперь часто сравнивают с квадратами, основанными на внутреннем и внешнем отрицании. [14]
Логические шестиугольники и другие бисимплексы
Квадрат оппозиции был расширен до логического шестиугольника, который включает отношения шести утверждений. Он был открыт независимо как Огюстеном Сесма (7 апреля 1885 г. – 12 декабря 1957 г.), так и Робером Бланше (1898–1975). [15] Было доказано, что и квадрат, и шестиугольник, за которыми следует « логический куб », принадлежат к регулярной серии n-мерных объектов, называемых «логическими би-симплексами размерности n ». Эта закономерность выходит даже за эти рамки. [16]
Квадрат оппозиции (или логический квадрат) и модальная логика
Логический квадрат, также называемый квадратом оппозиции или квадратом Апулея , берет свое начало в четырех отмеченных предложениях, которые используются в силлогистических рассуждениях: «Каждый человек плох», общеутвердительное — Отрицание общеутвердительного «Не каждый человек плох» (или «Некоторые люди не плохи») — «Некоторые люди плохи», частное утверждение — и, наконец, отрицание частного утверждения «Ни один человек не плох». Робер Бланше опубликовал с Врином свои Structures intellectuelles в 1966 году, и с тех пор многие ученые считают, что логический квадрат или квадрат оппозиции, представляющий четыре значения, следует заменить логическим шестиугольником , который, представляя шесть значений, является более мощной фигурой, поскольку он обладает силой объяснять больше вещей о логике и естественном языке.
Теоретико-множественная интерпретация категорических утверждений
В современной математической логике утверждения, содержащие слова «все», «некоторые» и «нет», могут быть сформулированы в терминах теории множеств, если мы предположим, что область дискурса подобна множеству. Если множество всех A обозначено как , а множество всех B как , то:
- «Все A есть B » (AaB) эквивалентно « является подмножеством » , или .
- «Ни одно A не является B » (AeB) эквивалентно « Пересечение и пусто » , или .
- «Некоторое A есть B » (AiB) эквивалентно «Пересечение и не пусто» или .
- «Некоторые A не являются B » (AoB) эквивалентно « не является подмножеством », или .
По определению, пустое множество является подмножеством всех множеств. Из этого факта следует, что, согласно этому математическому соглашению, если нет A 's, то утверждения "Все A есть B " и "Ни один A не есть B " всегда истинны, тогда как утверждения "Некоторые A есть B " и "Некоторые A не есть B " всегда ложны. Это также подразумевает, что AaB не влечет AiB, и некоторые из упомянутых выше силлогизмов недействительны, когда нет A 's ( ).
Смотрите также
- Силлогистика Буля
- Свободная логика
- Логический куб
- Логический шестиугольник
- Октагон Пророчеств
- Треугольник оппозиции
Ссылки
- ^ Согласно «Традиционному квадрату оппозиции»: 1.1. Современная редакция квадрата в Стэнфордской энциклопедии философии
- ^ Келли, Дэвид (2014). Искусство рассуждения: Введение в логику и критическое мышление (4-е изд.). Нью-Йорк, Нью-Йорк: WW Norton & Company, Inc. стр. 150. ISBN 978-0-393-93078-8.
- ^ «Введение в логику — 7.2.1 Завершение квадрата и непосредственные выводы». 2021-08-10.
- ↑ Пэрри и Хакер, Аристотелевская логика (SUNY Press, 1990), стр. 158.
- ^ Коэн и Нагель, Введение в логику, второе издание (Hackett Publishing, 1993), стр. 55.
- ^ Реале, Джованни ; Антисери, Дарио (1983). Западный мыслитель был в прошлом году . Том. 1. Брешия: Эдитрис Ла Скуола. п. 356. ИСБН 88-350-7271-9. OCLC 971192154.
- ^ Массаро, Доменико (2005). Вопросы истины: базовая логика для чтения и фарси. Сценарий (на итальянском языке). Том. 2. Клены: Liguori Editore Srl. п. 58. ИСБН 9788820738921. LCCN 2006350806. OCLC 263451944.
- ↑ В своей работе «Диалектика» и в комментариях к « Перигермании»
- ^ Re enim hominis prorsus нон экзистенте neque ea vera est quae ait: omnis homo est homo, nec ea quae proponit: quidam homo non est homo
- ^ Si enim vera est: Omnis homo qui lapis est, est lapis, et eius conversa per Accidens Vera est: Quidam lapis est homo qui est lapis. Sed nullus lapis est homo qui est lapis, quia neque hic neque ille и т. д. Sed et illam: Quidam homo qui est lapis, non est lapis, falsam esse necesse est, cum impossibile ponat
- ^ в Традиционном квадрате оппозиции в Стэнфордской энциклопедии философии
- ^ (SL I.72) Лу 1974, 206
- ^ Традиционная площадь оппозиции
- ^ Вестерстоль, «Классические и современные квадраты оппозиции и не только», в книге Безьяу и Пайетта (ред.), Квадрат оппозиции: общая структура познания, Питер Ланг, Берн, 195-229.
- ^ Теория N-оппозиции Логический шестиугольник
- ^ Моретти, Пеллиссье
Внешние ссылки
- Парсонс, Теренс. «Традиционный квадрат оппозиции». В Zalta, Эдвард Н. (ред.). Стэнфордская энциклопедия философии .
- Международный конгресс на площади Оппозиции
- Специальный выпуск Logica Universalis Vol. 2 N. 1 (2008) на площади Оппозиции
- Catlogic: компьютерный скрипт с открытым исходным кодом, написанный на Ruby для построения, исследования и вычисления категориальных суждений и силлогизмов.
- Periermenias Aristotelis со ссылками на видео и оцифрованную рукопись LJS 101 латинского перевода Боэция сочинения Аристотеля De interpretatione , которая содержит копии IX/XI веков (некоторые цветные) квадрата оппозиции Аристотеля на листах 36r и 36v.

















