Последовательность «Посмотри и скажи»

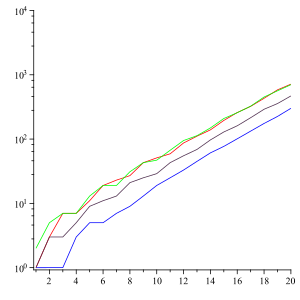
В математике последовательность « посмотри и скажи» — это последовательность целых чисел, начинающаяся следующим образом:

1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, 31131211131221, ... (последовательность A005150 в OEIS ).

Чтобы сгенерировать член последовательности из предыдущего члена, считайте цифры предыдущего члена, подсчитывая количество цифр в группах одной и той же цифры. Например:

• 1 читается как «один 1» или 11.
• 11 читается как «две единицы» или 21.
• 21 читается как «один 2, один 1» или 1211.
• 1211 читается как «одна 1, одна 2, две 1» или 111221.
• 111221 читается как «три единицы, две двойки, одна единица» или 312211.

Последовательность «посмотри и скажи» была проанализирована Джоном Конвеем ^[1] после того, как один из его студентов познакомил его с ней на вечеринке. ^{[2] [3]}

Идея последовательности «посмотри и скажи» аналогична идее кодирования длин серий .

Если начать с любой цифры d от 0 до 9, то d останется последней цифрой последовательности на неопределенный срок. Для любой цифры d, отличной от 1, последовательность начинается следующим образом:

д , 1 д , 111 д , 311 д , 13211 д , 111312211 д , 31131122211 д , …

Илан Варди назвал эту последовательность, начинающуюся с d = 3, последовательностью Конвея (последовательность A006715 в OEIS ). (для d = 2 см. OEIS : A006751 ) ^[4]

Последовательность растет бесконечно. Фактически, любой вариант, определенный путем начала с другого целого числа-источника, (в конечном итоге) также будет расти бесконечно, за исключением вырожденной последовательности: 22, 22, 22, 22, ..., которая остается того же размера. ^[5]

В последовательности не встречаются никакие цифры, кроме 1, 2 и 3, если только начальное число не содержит такую ​​цифру или серию из более чем трех одинаковых цифр. ^[5]

Космологическая теорема Конвея утверждает, что каждая последовательность в конечном итоге распадается («распадается») на последовательность «атомных элементов», которые являются конечными подпоследовательностями, которые никогда больше не взаимодействуют со своими соседями. Существует 92 элемента, содержащих только цифры 1, 2 и 3, которые Джон Конвей назвал в честь 92 встречающихся в природе химических элементов вплоть до урана , назвав последовательность аудиоактивной . Также существует два « трансурановых » элемента (Np и Pu) для каждой цифры, кроме 1, 2 и 3. ^{[5] [6]} Ниже приведена таблица всех таких элементов:

Термины в конечном итоге увеличиваются в длину примерно на 30% за поколение. В частности, если L _n обозначает количество цифр n -го члена последовательности, то предел отношения существует и задается как${\displaystyle {\frac {L_{n+1}}{L_{n}}}}$$${\displaystyle \lim _{n\to \infty }{\frac {L_{n+1}}{L_{n}}}=\lambda }$$

где λ = 1,303577269034... (последовательность A014715 в OEIS ) — алгебраическое число степени 71. ^[5] Этот факт был доказан Конвеем, а константа λ известна как константа Конвея . Тот же результат справедлив для любого варианта последовательности, начинающегося с любого семени, отличного от 22.

Константа Конвея — это единственный положительный действительный корень следующего полинома (последовательность A137275 в OEIS ):$${\displaystyle {\begin{matrix}&&\qquad &&\qquad &&\qquad &&+1x^{71}&\\-1x^{69}&-2x^{68}&-1x^{67}&+2x^{66}&+2x^{65}&+1x^{64}&-1x^{63}&-1x^{62}&-1x^{61}&-1x^{60}\\-1x^{59}&+2x^{58}&+5x^{57}&+3x^{56}&-2x^{55}&-10x^{54}&-3x ^{53}&-2x^{52}&+6x^{51}&+6x^{50}\\+1x^{49}&+9x^{48}&-3x^{47}&-7x^{46}&-8x^{45}&-8x^{44}&+10x^{43}&+6x^{42}&+8x^{41}&-5x^{40}\\-12x^{39}&+7x^{38}&-7x^{37}&+7x^{36} &+1x^{35}&-3x^{34}&+10x^{33}&+1x^{32}&-6x^{31}&-2x^{30}\\-10x^{29}&-3x^{28}&+2x^{27}&+9x^{26}&-3x^{25}&+14x^{24}&-8x^{23}&&-7x^{21}&+9x^{20}\\+3x^{19}&-4x^{18}&-1 0x^{17}&-7x^{16}&+12x^{15}&+7x^{14}&+2x^{13}&-12x^{12}&-4x^{11}&-2x^{10}\\+5x^{9}&&+1x^{7}&-7x^{6}&+7x^{5}&-4x^{4}&+12x^{3}&-6x^{2}&+3x^{1}&-6x^{0}\\\end{matrix}}}$$

Этот многочлен был правильно указан в оригинальной статье Конвея в журнале «Эврика» ^[1] , но в перепечатанной версии в книге под редакцией Ковера и Гопината ^[1] термин был неправильно напечатан со знаком минус впереди. ^[7]${\displaystyle x^{35}}$

Последовательность «посмотри и скажи» также широко известна как последовательность чисел Морриса , в честь криптографа Роберта Морриса , а головоломка «Какое следующее число в последовательности 1, 11, 21, 1211, 111221?» иногда называется « Яйцо кукушки» , по описанию Морриса в книге Клиффорда Столла «Яйцо кукушки» . ^{[8] [9]}

В этом разделе не указаны источники . Пожалуйста, помогите улучшить этот раздел , добавив ссылки на надежные источники . Материалы без ссылок могут быть оспорены и удалены . ( Май 2022 г. ) ( Узнайте, как и когда удалять это сообщение )

Существует множество возможных вариаций правила, используемого для генерации последовательности «посмотри и скажи». Например, для формирования «шаблона гороха» считывается предыдущий термин и подсчитываются все экземпляры каждой цифры, перечисленные в порядке их первого появления, а не только те, которые встречаются в последовательном блоке. Таким образом, начиная с семени 1, шаблон гороха продолжается 1, 11 («одна 1»), 21 («две 1»), 1211 («одна 2 и одна 1»), 3112 («три 1 и одна 2»), 132112 («одна 3, две 1 и одна 2»), 311322 («три 1, одна 3 и две 2») и т. д. Эта версия шаблона гороха в конечном итоге образует цикл с двумя «атомарными» терминами 23322114 и 32232114.

Возможны и другие версии узора гороха; например, вместо того, чтобы читать цифры так, как они появляются в первый раз, можно читать их в порядке возрастания (последовательность A005151 в OEIS ). В этом случае термин, следующий за 21, будет 1112 («одна 1, одна 2»), а термин, следующий за 3112, будет 211213 («две 1, одна 2 и одна 3»). Этот вариант в конечном итоге заканчивается повторением числа 21322314 («две 1, три 2, две 3 и одна 4»).

Эти последовательности отличаются несколькими заметными способами от последовательности «посмотри и скажи». Примечательно, что в отличие от последовательностей Конвея, заданный член шаблона гороха не определяет однозначно предыдущий член. Более того, для любого семени шаблон гороха создает члены ограниченной длины: эта граница обычно не превышает 2 × Radix + 2 цифры (22 цифры для десятичной системы счисления : основание = 10 ) и может превышать только 3 × Radix цифры (30 цифр для десятичной системы счисления) по длине для длинных, вырожденных, начальных семян (последовательность из «100 единиц» и т. д.). Для этих крайних случаев отдельные элементы десятичных последовательностей немедленно укладываются в перестановку вида a 0 b 1 c 2 d 3 e 4 f 5 g 6 h 7 i 8 j 9 , где здесь буквы a – j являются заполнителями для количества цифр из предыдущего элемента последовательности.

Поскольку последовательность бесконечна, а длина каждого элемента ограничена, она должна в конечном итоге повториться, согласно принципу ящика . Как следствие, последовательности гороховых узоров всегда в конечном итоге периодические .

• Последовательность Гейсвейта
• последовательность Колакоски
• Автограмма

• Конвей рассказал об этой последовательности и сообщил, что ему потребовались некоторые объяснения, чтобы понять ее.
• Реализации на многих языках программирования на Rosetta Code
• Вайсштейн, Эрик В. «Посмотри и назови последовательность». MathWorld .
• Генератор последовательностей «Посмотри и скажи» p
• Последовательность OEIS A014715 (Десятичное разложение константы Конвея)
• Вывод полинома Конвея степени 71 «Посмотри и скажи»